- Spaceone

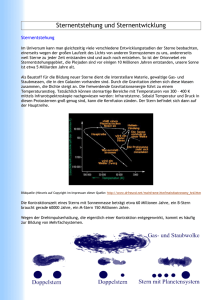
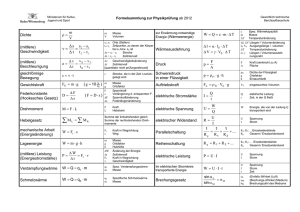
Sternaufbau
Für eine theoretische Modellierung des Sternaufbaus werden zunächst elementare
Vereinfachungen und Idealisierungen getroffen.
Der Stern sei ein kugelsymmetrischer Körper und befinde sich im hydrostatischen
Gleichgewicht. Diese Bedingung ist für alle Sterne gegeben, wenn sie sich in der
Hauptreihenphase ihres Lebens aufhalten. Abweichungen von der Kugelsymmetrie
werden oft durch hohe Rotationsraten bedingt, die zu einem
geschwindigkeitsabhängigen Abplatten an den Polen führen.
Wir nehmen weiterhin an, dass keinerlei magnetische Kräfte auf den Stern wirken
und sein Zustand durch ein ideales Gas beschrieben werden kann. Darüber hinaus
wird seine Masse als konstant angenommen, und lokales thermisches Gleichgewicht
postuliert. Dabei gibt jeder beliebig gewählte Punkt im Sterninnern genau so viel
Energie durch Abstrahlung ab, wie durch Wärmeaustausch auf. Aufgrund der im
Verhältnis zur Temperaturänderung kleinen freien Weglänge der Photonen, ist diese
Näherung insbesondere im tiefen Sterninnern hinreichend gut gegeben. Magnetische
Kräfte spielen bei massearmen G, K und M-Sternen eine wichtige Rolle, da sie die
Dynamik der Sternmaterie beeinflussen. Die Massenfunktion der Sterne ist
strenggenommen ebenfalls nicht konstant, sondern ändert sich durch
strahlungsgetriebene Winde und nukleare Energieerzeugungsraten, insbesondere sehr
stark, bei den massereichen Sternen.
Wir betrachten nun einen kugelsymmetrischen Körper mit der Masse M und dem
Radius R.
Zur genaueren Abschätzung über die Zustandsgrößen im Sterninnern, wird der Stern
selber in Kugelschalen unterteilt. Eine Kugelschale habe die Dicke dr und die Masse
dm. Sie befindet sich außerdem in einem Abstand r vom stellaren Zentrum, und wird
von der unter ihr eingeschlossenen Masse m gravitativ beeinflusst. Nach den
Gesetzen der Physik gilt allgemein:
M
=ρ
V
(1)
M =V ∘ρ
(2)
Und damit weiterhin:
Die innerhalb der Kugelschale eingeschlossene Masse ergibt sich mit ihrem Volumen
damit zu:
dm
=4 π r²∗ρ(r )
dr
(3)
Diese erste Grundgleichung des Sternaufbaus beschreibt das Prinzip der
Massenerhaltung. Eine Integration über den gesamten Radius R, lieferte die
Gesamtmasse M. Eine weitere Gleichung beschreibt den pro Fläche Sternmaterie
ausgeübten Druck in der Kugelschale. Nach dem Birkhoff-Theorem, trägt nur
diejenige Masse M(r) zur Gravitationsbeschleunigung g bei, die sich noch innerhalb
von r befindet. Im allgemeinen Fall gilt für g:
g ( r )=
G∗m(r )
r²
(4)
Da die Gravitationskraft vektoriell auf das Zentrum des Sterns zielt, und die Dichte
der Kugelschale nicht zu vernachlässigen ist gilt:
dp −ρ∗G∗m( r )
=
dr
r²
(5)
Dieser auch als hydrostatische Gleichung bekannte Ausdruck beschreibt schließlich
die Druckverteilung in der betrachteten Schichtung. Er stellt die zweite wichtige
Grundgleichung des Sternaufbaus dar.
Unsere weitere Argumentation besteht in der Annahme einer Druckdifferenz
zwischen dem oberen (Pe) und dem unteren Ende (Pi) der betrachteten Kugelschale.
Wenn die in der Schichtung enthaltenen Massenelemente in keine Beschleunigung
versetzt werden sollen, muss für die Druckdifferenz über eine Wegstrecke dr gelten:
Pi−Pe=
−Δ P
∗dr
Δr
(6)
Neben der Druckdifferenz muss die Gravitationsbeschleunigung berücksichtigt
werden. Im Falle des hydrostatischen Gleichgewichtes kompensieren sich beide
Kräfte, und die Materie verharrt im Ruhezustand.
Nach dem Gleichsetzen finden für die Bedingung des hydrostatischen
Gleichgewichts im Sterninnern:
Δ P −G∗m
=
Δ m 4πr4
(7)
Aus dieser Bedingung können wir unter Verwendung eines Dichtegesetzes bereits
elementare Abschätzungen über die Zustandsgrößen im Sterninnern gewinnen. Unter
der Annahme einer konstanten Sterndichte erhalten wir aus Gleichung 7, durch das
Ersetzen von m und r durch m/2 und r/2:
Pc=
2GM²
π R4
(8)
Unter der Annahme eines idealen Gases gilt für die mittlere Dichte des Sterns:
ϱ=
3M
4 π R3
(9)
Für die Zentraltemperatur im Sternkern muss gelten:
Tc=
Pc μ
μ ϱ 4 π r³
=Pc Μ
Μ
ϱc
ϱ c 3M
(10)
Ist ein Teil der Gravitationskraft in der Bedingung des hydrostatischen
Gleichgewichts, nicht durch entsprechende Druckkräfte ausgeglichen, so wird die
dort befindliche Materie in eine Beschleunigung versetzt. Die Bewegungsgleichung
für sphärisch symmetrische Körper geht dann über zu:
E=mc2
(11)
Wird die Stabilitätsbedingung durch die Anregung innerer Freiheitsgrade verletzt, so
findet durch den Entfall der Gravitationskraft eine Beschleunigung der Sternmaterie,
in Form eines freien Falls ab. Die Dauer des Sternkollaps wird abgeschätzt, indem die
hydrostatische Grundgleichung um den Beschleunigungsterm aus 11 erweitert wird.
Dann gilt für die Freifallzeit tff:
tff ≈
√
1
Gϱ
(12)
Für unsere Sonne finden wir einen Wert von etwa 1 Stunde. Für einen Roten Riesen
wird tff anlässlich der geringeren Dichte wesentlich größer.
Zusätzlich zur dynamischen Zeitskala führen wir eine weitere Größe ein, die
beschreibt, wie lange ein Stern Strahlungsverluste durch die potenzielle Energie des
Gravitationsfeldes decken kann. Die Gravitationsenergie wird nach dem Virialsatz
eng mit seiner thermischen Energie verknüpft. Bei Systemen mit gravitierenden
Massenpunkten ist im Zeitintervall die kinetische Energie auf folgende Weise mit der
potenziellen Energie verknüpft:
Ekin=
−1
Epot
2
(13)
Im Fall einer homogenen Kugel wird die potenzielle Energie des Gravitationsfeldes
somit:
Epot =
GM²
R
(14)
Eine völlige Ausschöpfung der Gravitationsenergie über ein Zeitintervall t führt auf
die Zeit in der ein Stern Leuchtkraftverluste alleine durch seine Gravitationsenergie
decken kann. Für die Kelvin-Helmholtz-Zeit findet man:
tkh≈
GM²
RL
(15)
Diese Zeitskala ist insbesondere für junge Protosterne und T-Tauri-Veränderliche
relevant, die im Kern nach Gleichung 10 noch nicht heiß genug sind um
thermonukleare Fusionsketten zu zünden. Sie decken ihre Strahlungsverluste durch
die Gravitationsenergie. Für die Sonne ist tkh von der Größenordnung ~ 15 Millionen
Jahre. Der Virialsatz zeigt uns, dass bei einer Kontraktion des Sterns, die Hälfte
seiner Gravitationsenergie in Strahlung umgewandelt wird, und die andere Hälfte zur
inneren Aufheizung verwendet werden kann.
Kommen wir noch auf die Bedeutung der Zustandsgleichung zu sprechen. Diese
Gleichung verbindet im Stern, Temperatur, Druck und Dichte miteinander. Im Fall
von Hauptreihensterne, darf dafür die allgemeine Gasgleichung verwendet werden.
ρκT
pg = μ
(16)
Dabei ist u die mittlere molare Masse, die in erster Linie vom Ionisationsgrad der
Sternmaterie abhängt. Im Innern eines Sterns ist vollständige Ionisation grundsätzlich
vollständig gegeben. In den äußeren Schichten, insbesondere bei Sternen der
Spektralklasse K oder M, sind die Elemente vielfach nur noch teilweise ionisiert. Der
Wert von u ist darum schwierig zu ermitteln und häufig nur numerisch herzuleiten.
Der Gasdruck pg ist mathematisch gesehen, das erste Argument, dass in der
Bedingung des hydrostatischen Gleichgewichts, der Gravitationskraft entgegenwirkt.
Im Fall eines massereichen Sterns (ab etwa 5 Sonnenmassen), wird neben dem
Gasdruck aber auch der Strahlungsdruck relevant, der alleinige Funktion der
Temperatur ist. Als allgemeine Bedingung erhält man aus den obigen Gleichungen:
L ~ M^3,5
T ~ M^0,6
r ~ T^2/3
Wie wir sehen, steigt die Temperatur eines Sterns also proportional zur Masse hoch
0,6. Da der Strahlungsdruck alleinige Funktion der Temperatur ist, gilt für ps:
1
4
Ps= a T
3
(17)
Kommen wir nun auf die Mechanismen des Energietransports zu sprechen. Die
Temperaturschichtung des Sterns ist empfindlich davon abhängig. Im allgemeinen
führt schlechter Energietransport zu einem steilen Temperaturgradienten, guter
Energietransport zu einem flacheren Temperaturgradienten. Energietransport über
Strahlung erfolgt in Bereichen, in denen der adiabatische Temperaturgradient den
radiativen Gradienten im Wert übersteigt. Umgekehrt kommt es zu
Konvektionsprozessen, wenn der radiative Gradient, den adiabatischen Wert
übersteigt. Radiativer Transport kann über die Diffusionsnäherung beschrieben
werden, da im allgemeinen von einem isotropen Strahlungsfeld im Sterninnern
auszugehen ist. Die gesamte Strahlungsenergie, die in einer Zeiteinheit durch eine
Kugelfläche vom Radius r transportiert wird, ergibt sich schließlich zu:
L(r )=4 π r² F =
−16 π acr² T³ dT
κ ϱ dr
3
(18)
An der Oberfläche des Sterns geht L(r) zur Gesamtleuchtkraft L über. Der radiative
Energietransport beschreibt nach dieser Gleichung, wie viel Energie entlang einer
Wegstrecke transportiert werden kann, wenn dort eine Temperaturdifferenz
vorhanden ist. Die Wechselwirkung an freien Elektronen (Compton-Effekt) und die
damit einergehenden Prozesse wie Absorption, Streuung und Reemission fließen alle
in die Beschreibungen des Energietransports ein, und unterbinden effizienten
schnellen Abtransport nach außen. Wenn in einem bestimmten Intervall die
Temperaturdifferenz entlang einer Wegstrecke sehr groß wird, und sie somit den
adiabatischen Wert übertrifft, setzt Konvektion in der Schicht ein. Für den
adiabatischen Temperaturgradienten finden wir:
dT
1 T dP
=(1− )
dr
y P dr
(19)
Das ist der Temperaturgradient einer Konvektionszone. Im allgemeinen muss dieser
Wert den radiativen Gradienten aus 18 übertreffen um die Schichtung instabil werden
zu lassen. Um zu testen, welcher Mechanismus in einer Schichtung im Stern jeweils
effizient ist, wird ein Massenelement vom Level dr auf ein höheres Niveau dr + d
gehoben. Schließlich bestimmt das weitere Verhalten des Elements über die Stabilität
der betroffenen Schichtung.
Die erste Möglichkeit für das Element besteht darin, nach dem Aufstieg, wieder
abzusinken. Das ist der Fall, wenn die Temperaturänderung im Massenelement über
die Aufstiegstrecke d im Vergleich zur Umgebung größer ist. Das Element sinkt
schließlich wieder ab, und nimmt aus der Schicht Massenträgheit auf. Am unteren
Ende des Niveaus (bei dr) fängt es anlässlich des Exzesses an zu pulsieren. Diese
adiabatische Osillation wird mit der Brunt-Väisälä-Frequenz beschrieben. Eine solche
Schichtung ist mathematisch gesehen dynamisch stabi. Folglich ist der
vorherrschende Energietransportmechanismus die Radiation.
Wenn die Temperaturänderung des aufsteigenden Elementes im Vergleich zur
Umgebung über die Wegstrecke d kleiner ausfällt, so wird das Massenelement auf
dem Lever dr + dr, einen Temperaturexzess besitzen und folglich weiter aufsteigen.
Diese Schichtung ist dynamisch instabil. Hier setzen Konvektionsprozesse ein. Für
einen ständigen Konvektionsstrom muss die Temperaturänderung des auf- bzw.
absteigenden Elementes also kleiner sein, als die durchschnittliche
Temperaturänderung in der im Strahlungsgleichgewicht befindlichen Umgebung.
Eine Instabilität der Schichtung wird unter anderem durch hohe Werte der Opazität
verursacht, die besonders dann in Erscheinung tritt, wenn teilweise Ionisation oder
Dissoziation zu einer Verkleinerung von y in Gleichung 19 führt. Eine Herabsetzung
des radiativen Gradienten wird beobachtet, wenn in Gleichung 18, das
Temperaturgefälle über eine Wegstrecke dr vergleichsweise flach ausfällt.
Bei Hauptreihensternen, werden abhängig von ihrer Masse und der damit
einergehenden Temperaturschichtung unterschiedliche Fälle beobachtet. Sterne mit
einer Masse von M < 0,5 Sonnenmassen sind über alle Volumenelemente gemittel,
dynamisch instabil und folglich vollkonvektiv. Sterne zwischen 0,6 und 1,4
Sonnenmassen besitzen Kerntemperaturen, bei denen die Proton-Proton-Reaktion als
Energiequelle dominiert. Vom Kern ausgehend finden wir dort einen flacheren
Temperaturverlauf. Folglich ist der radiative Gradient klein im Vergleich zum
adiabatischen Gradienten. Die Radiation dominiert, bis zu einem Radius von etwa
71%. Danach beginnen die beteiligten Wasserstoffkerne, die individuelle Anziehung
zu den Elektronen zu bemerken, was zu einer Verkleinerung der Opazität führt.
Sterne wie unsere Sonne besitzen somit einen radiativen Kern, an den eine
Konvektionszone anschließt.
Schließlich findet man für Sterne mit M > 1,5 Sonnenmassen, Kerntemperaturen von
22 * 10^6 Kelvin aufwärts. Dort dominiert der CNO-Zyklus als dominierende
Energiequelle, der in einem sehr schmalen Bereich hohe Energiedichten erfordert um
funktionieren zu können. Sterne mit mehr als 1,5 Sonnenmassen besitzen daher einen
konvektiven Kern, und einen radiativen Umschlag.