Leseprobe - Christiani
Werbung

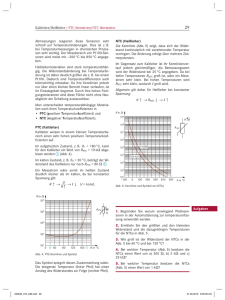
28 Messen Thermische Größen / thermal parameters 1.5.2 Temperaturabhängige Widerstände 1.5 Erfassung thermischer Größen In den in der Automatisierung eingesetzten Widerstandsmessfühlern werden unterschiedliche temperaturabhängige Widerstände verwendet. Dabei wird der Effekt ausgenutzt, dass sich der Widerstand z. B. eines Metalls in Abhängigkeit von der Temperatur verändert. 1.5.1 Grundlagen Temperatursensoren werden in passive und aktive Sensoren unterschieden. Als passive Sensoren werden in der Regel temperaturabhängige Widerstände verwendet. Diese verändern also ihren Widerstand in Abhängigkeit der Temperatur und erzeugen kein eigenständiges verwertbares Signal. Aktive Sensoren hingegen stellen ein der Temperatur proportionales Signal zur Verfügung. Dabei gilt für den Widerstand RT eines metallischen Leiters bei einer bestimmten Temperatur folgende Formel: RT = R20 · (1 + α · ∆T) R20: Widerstand des Leiters bei 20 °C. α: Temperaturkoeffzient (Platin: α = 0,004 1/K) Ist der Temperaturkoeffizient größer als Null, spricht man von einem positiven, ist er kleiner als Null, von einem negativen Temperaturkoeffizienten. ∆T: Temperaturänderung bezogen auf 20 °C in K. Passive Temperatursensoren werden in einer Brückschaltung in Zwei-, Drei- oder Vierleitertechnik betrieben: Zweileitertechnik Bei der Zweileitertechnik (Abb. 2a) sind der Sensor und die Auswerteschaltung gemeinsam mit einer zweiadrigen Leitung verbunden. Da der Leiterwiderstand und der Sensor in Reihe liegen, kommt es zu einer Messwertverfälschung. Für Widerstandsmessfühler wird vor allem Platin eingesetzt, da es über eine sehr lineare Kennlinie verfügt. Auch bei häufiger Erwärmung und Abkühlung behält es seinen ursprünglichen Widerstandswert nahezu bei. Der so genannte Bemessungswiderstand ist bei 0 °C definiert. Für Widerstandsmessfühler ist er genormt und beträgt 100 Ω, 200 Ω, 500 Ω oder 1000 Ω. Daraus lässt sich z. B. auch die Bezeichnung Pt100 (PlatinMessfühler mit 100 Ω Bemessungswiderstand) ableiten. Die Kennlinie ist im Bereich von –100 °C bis 400 °C nahezu linear (Abb. 3). Dreileitertechnik Bei der Dreileitertechnik (Abb. 2b) wird ein zusätzlicher Leiter zum Sensor geführt, sodass zwei Messkreise entstehen. Der Leiterwiderstand sowie seine Temperaturabhängigkeit lassen sich kompensieren. Vierleitertechnik Bei der Vierleitertechnik (Abb. 2c) fliest durch den Sensor ein konstanter Strom. Der Spannungsfall am Sensor wird abgegriffen und an den Eingang einer hochohmigen Auswerteschaltung geführt. Leiterwiderstände und deren Temperaturabhängigkeit sind weitgehend ohne Einfluss. R in Ω 250 200 150 100 50 0 –100 Temperatursensoren Halbleiter PTC Pt100 Halbleiter PTC 0 ϑ in °C 100 200 300 400 Abb. 3: Kennlinie eines Pt100 Messfühlers Thermoelement Das Widerstandsmaterial wird bei diesem Messfühler auf ein Trägermaterial gewickelt. Bei Miniaturausführungen wird das Platin auf eine Keramikfläche aufgedampft. Aufgrund der geringen Abb. 1: Beispiele für Temperatursensoren RL R1 RL RM RL R2 + – R3 RL UA UB RM R1 + – RL IB = konst. R2 R3 UA + – UB RM RL a) Zweileitertechnik b) Dreileitertechnik c) Vierleitertechnik Abb. 2: Anschluss eines Temperatursensors (rot = Sensor, blau = Auswerteschaltung) UA UB 29 Kaltleiter/Heißleiter / PTC thermistor/NTC thermistor Abmessungen reagieren diese Sensoren sehr schnell auf Temperaturänderungen. Dies ist z. B. bei Temperaturmessungen in chemischen Prozessen sehr wichtig. Der Messbereich von Pt100-Sensoren wird meist mit –200 °C bis 850 °C angegeben. Halbleitermaterialien sind stark temperaturabhängig. Die Widerstandsänderung bei Temperaturänderung ist daher deutlich größer als z. B. bei einem Pt100. Dadurch sind Temperaturdifferenzen auch kleinschrittig erfassbar. Da ihre Kennlinien jedoch nur über einen kleinen Bereich linear verlaufen, ist ihr Einsatzgebiet begrenzt. Durch ihre hohen Fertigungstoleranzen sind diese Fühler nicht ohne Neuabgleich der Schaltung austauschbar. Man unterscheidet temperaturabhängige Materialien nach ihren Temperaturkoeffizienten in • PTC (positiver Temperaturkoeffizient) und • NTC (negativer Temperaturkoeffizient). PTC (Kaltleiter) Kaltleiter weisen in einem kleinen Temperaturbereich einen sehr hohen positiven Temperaturkoeffizienten auf. Im aufgeheizten Zustand, z. B. ϑ1 = 180 °C, kann für den Kaltleiter ein Wert von RPTC = 10 kΩ abgelesen werden 1 (Abb. 4). Im kalten Zustand, z. B. ϑ2 = 20 °C, beträgt der Widerstand des Kaltleiters nur noch RPTC = 80 Ω 2. Ein Messstrom wäre somit im heißen Zustand deutlich kleiner als im kalten, da bei konstanter Spannung gilt: U R ↑ → ____ → I ↓ U = konst. R↑ NTC (Heißleiter) Die Kennlinie (Abb. 5) zeigt, dass sich der Widerstand kontinuierlich mit zunehmender Temperatur verringert. Die Änderung erfolgt über mehrere Zehnerpotenzen. Im Gegensatz zum Kaltleiter ist ihr Kennlinienverlauf jedoch gleichmäßiger. Als Bemessungswert wird der Widerstand bei 25 °C angegeben. Da bei tiefen Temperaturen RNTC groß ist, wäre ein Messstrom sehr klein. Bei hohen Temperaturen wird RNTC sehr klein, wodurch I groß wird. Allgemein gilt daher für Heißleiter bei konstanter Spannung: ϑ ↑ → RNTC ↓ → I ↑ R in Ω 109 ϑ 2 108 R NTC 107 1 106 1 MΩ 105 104 100 kΩ 103 102 101 –100 0 100 200 300 400 500 ϑ in °C Abb. 5: Kennlinie und Symbol von NTCs R in Ω 105 R PTC 104 ϑ 103 2. Ermitteln Sie den größten und den kleinsten Widerstand und die dazugehörigen Temperaturen für die NTCs in Abb. 5. 102 101 1. Begründen Sie warum vorwiegend Platinsensoren in der Automatisierung zur temperaturerfassung verwendet werden. 3. Wie groß ist der Widerstand der NTCs in der Abb. 5 bei 60 °C und bei 130 °C? 0 2 40 80 120 160 1 ϑ in °C Abb. 4: PTC-Kennlinie und Symbol 4. Bei welcher Temperatur (Abb. 5) besitzen die NTCs einen Wert von a) 300 Ω, b) 2 kΩ und c) 25 kΩ? Das Symbol spiegelt diesen Zusammenhang wider. Die steigende Temperatur (linker Pfeil) hat einen Anstieg des Widerstandes zur Folge (rechter Pfeil). 5. Bei welcher Temperatur besitzen die NTCs (Abb. 5) einen Wert von 1 kΩ? Aufgaben 85 Stromwender / commutator Stromwender (Kommutator) Der Kommutator besteht aus voneinander isolierten Kupfersegmenten, die mit der Ankerwicklung verbunden sind. Auf ihm schleifen die aus Kohle gefertigten Bürsten. Diese Bürsten sind Verschleißteile, die in regelmäßigen Intervallen ersetzt werden müssen. Im Klemmenkasten befinden sich die Anschlüsse für den Anker und für die Erregerwicklung. Ankerrückwirkung Um die Verzerrungen durch das Ankerfeld auszugleichen, werden wie beim Generator (s. Kap. 2.4.1) Wendepol- und Kompensationswicklungen eingefügt (Abb. 3). Sie werden in Reihe mit der Ankerwicklung geschaltet. Kompensationswicklung MWelle↑ ⇒ n ↓ ⇒ UG ↓ ⇒ IA ↑ ⇒ ΦA ↑ ⇒ MMotor↑ Die Größe der Gegenspannung UG errechnet sich aus der Bemessungsspannung UB und der Ankerspannung UA wie folgt: UG = UB – UA UA = RA · IA UG = UB – RA · IA RA: Ankerwiderstand UG UB RA UA Abb. 4: Gegenspannung beim Motor Beispiel: Gegenspannung und Ankerstrom Ein Gleichstrommotor für 220 V hat einen Ankerwiderstand von 0,5 Ω. b) Wie groß ist die Stromstärke in der Ankerwicklung im Moment des Anlaufs? S Geg.: UB = 220 V; RA = 0,5 Ω; IALeer = 2 A; IABel = 30 A Wendepol S IA M a) Welche Gegenspannung entwickelt der Motor, wenn die Ankerstromstärke im Leerlauf 2 A und unter Bemessungsbelastung 30 A beträgt? N N Durch die geringere Gegenspannung kann wiederum ein größerer Ankerstrom fließen, der ein stärkeres Magnetfeld aufbaut. Das vom Motor entwickelte Drehmoment steigt. Aus diesen Betrachtungen ergibt sich folgende Wirkungskette: Hauptpol Abb. 3: Feldverlauf im Motor Gegenspannung Dreht sich der Anker des Gleichstrommotors im Erregermagnetfeld, so wird auch in der Ankerwicklung eine Spannung induziert. Sie ist zur angelegten Betriebsspannung UB entgegengesetzt gerichtet und wird deshalb als Gegenspannung UG bezeichnet. Auswirkungen der Gegenspannung Im Moment des Motoranlaufs befinden sich die Ankerleiter noch im Stillstand. Da keine Flussänderung vorhanden ist, entsteht keine Induktionsspannung. Die Gegenspannung ist gleich Null. Sie steigt mit größer werdender Drehzahl (UG ~ n). Die Gegenspannung kann aber nie den Wert der Betriebspannung annehmen, da dann keine Spannung mehr im Anker vorhanden wäre (UB – UG = 0 V). Der Ankerstrom wäre dann gleich Null und damit wäre kein Ankermagnetfeld mehr vorhanden. Da die Gegenspannung von der Drehzahl des Ankers abhängt, ändert sie sich auch bei der Belastungsänderung des Motors. Wird er stärker belastet, sinkt seine Drehzahl. Folglich wird die Gegenspannung kleiner. Ges.: UGLeer in V; UGBel in V; IAnlauf in A a) UGLeer = UB – RA · IA; UGLeer = 220 V – 0,5 Ω · 2 A UGLeer = 219 V UGBel = UB – RA · IA; UGBel = 220 V – 0,5 Ω · 30 A UGBel = 205 V UB – UG b) UGAnlauf = UB – RA · IA; IA = _______ RA Da im Anlauf keine Gegenspannung herrscht (UG = 0), gilt 220 V – 0 V IA = __________ ; IA = 440 A 0,5 Ω Wie Teilaufgabe b) im vorangehenden Berechnungsbeispiel zeigt, ist die Anlaufstromstärke eines Gleichstrommotors sehr groß. Ursache ist die fehlende Gegenspannung im Einschaltmoment. Der Stromfluss wird nur durch den kleinen Ankerwiderstand begrenzt. n = 0 ⇒ UG = 0 V ⇒ UB = UA ⇒ IA ↑↑, da RA ↓↓ Der Motor kann deshalb nicht ohne weiteres direkt an das Versorgungsnetz angeschlossen werden. ! Der Anker erzeugt eine Gegenspannung, die der Klemmenspannung entgegengerichtet ist. Die Gegenspannung begrenzt die Ankerstromstärke. 86 Anlasswiderstände / starting resistors Anlasswiderstand Die einfachste Lösung zur Begrenzung der Anlaufstromstärke sind Anlasswiderstände (Abb. 1). Sie werden in Reihe zur Ankerwicklung geschaltet. Sobald der Motor seine Drehzahl erreicht hat, werden die Anlasswiderstände wieder aus dem Stromkreis entfernt. 2.4.2.2 Motorschaltungen Je nachdem wie Anker- und Statorspule (Erregerspule) zueinander geschaltet sind, ergeben sich die in Abb. 2 aufgeführten Gleichstrommotoren. Gleichstrommotoren Reihenschlussmotor Anker- und Statorspule sind in Reihe an eine gemeinsame Spannungsquelle angeschlossen Damit es zu einer möglichst gleichmäßigen Beschleunigung des Motors kommt, besitzen Anlasswiderstände mehrere Schaltstufen. ! Nebenschlussmotor Anker- und Statorspule sind parallel an eine gemeinsame Spannungsquelle angeschlossen Hohe Anlaufstromstärken bei Gleichstrommotoren werden durch Anlasswiderstände im Ankerstromkreis begrenzt. Bei Erreichen einer ausreichenden Drehzahl werden sie wieder entfernt. Doppelschlussmotor Anker- und Statorspule sind in Reihe an eine Spannungsquelle angeschlossen. Die zweite Statorspule ist dazu parallel geschaltet. Fremderregter Motor Anker- und Statorspule sind an verschiedenen Spannungsquellen angeschlossen Abb. 2: Motorarten Abb. 1: Anlasswiderstand Beispiel: Anlasswiderstand Für den Motor aus dem Beispiel auf der vorherigen Seite soll der Anlasswiderstand so berechnet werden, dass die 1,5-fache Bemessungsstromstärke (Imax = 1,5 · IA) im Einschaltmoment nicht überschritten wird. Geg.: UB = 220 V; RA = 0,5 Ω; IA = 30 A Ges.: RAnl in Ω Imax = 1,5 · IA; Imax = 1,5 · 30 A; Imax = 45 A Die einzelnen Wicklungen sind durch Buchstaben und Zahlen gekennzeichnet (Abb. 3). Der Motor besitzt • eine Ankerwicklung, • eine bzw. zwei Erregerfeldwicklungen (Reihenschluss- oder Nebenschlusswicklung bzw. Wicklung zur Fremderregung) sowie • Wendepol- und Kompensationswicklungen. In Installationsschaltungen werden die Wendepolund Kompensationswicklungen oft nicht mitgezeichnet, weil in der Regel die interne Verdrahtung nicht verändert werden kann. Rges = RAnl + RA; RAnl = Rges – RA C1 D2 C2 B1 B2 E2 A1 F2 U 220 V Rges = ; R = _____ ; Rges = 4,89 Ω Imax ges 45 A B ____ RAnl = Rges – RA ; RAnl = 4,89 Ω – 0,5 Ω ; RAnl = 4,39 Ω D1 E1 F1 M A2 B1 A1 – A2 Ankerwicklung D1 – D2 Reihenschlusswicklung E1 – E2 Nebenschlusswicklung B1 – B2 Wendepolwicklung Kompensationswicklung fremderregte Feldwicklung C1 – C2 B2 C1 Aufgaben Klemmen Bezeichnung F1 – F2 1. Ein Gleichstrommotor liegt an einer Spannung von 110 V. Die Gegenspannung beträgt 100 V bei einer Ankerstromstärke von 15 A. Berechnen Sie den Ankerwiderstand. 2. Berechnen Sie den Anlasswiderstand für einen Gleichstrommotor mit folgenden Kenndaten: Bemessungsspannung: 110 V Bemessungsstromstärke: 8 A Ankerwiderstand: 0,7 Ω Maximale Anlassstromstärke: 1,4-fache Bemessungsstromstärke C2 Abb. 3: Kennzeichnung der Anschlüsse L+ L– A1 M A2 B1 D1 D2 C1 B2 C2 Abb. 4: Reihenschlussmotor Reihenschlusswicklung