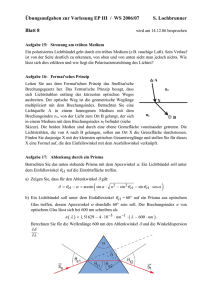
Plasmonverstärkte Licht-Molekül

Plasmonverstärkte
Licht-Molekül-Wechselwirkung in
metallischen Nanostrukturen
Diplomarbeit
zur Erlangung des akademischen Grades
einer Magistra der Naturwissenschaften
an der Karl-Franzens-Universität Graz
vorgelegt von
Rosa Dennig
am Institut für Physik, Fachbereich Theoretische Physik
Begutachter: Ao. Univ. Prof. Dr. Ulrich Hohenester
Graz, Dezember 2014
Inhaltsverzeichnis
Einleitung
4
1 Grundlagen
6
1.1
Elektromagnetisches Spektrum . . . . . . . . . . . . . . . . . . . . . . . .
6
1.2
Maxwellgleichungen und elektromagnetische Felder . . . . . . . . . . . .
7
1.3
Wellengleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.4
Schichtsystem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
1.4.1
Elektromagnetische Felder im Schichtsystem . . . . . . . . . . .
11
1.4.2
Fresnelkoeffizienten, Reflektivität und Transmittivität
1.5
eines N-Schichtsystems . . . . . . . . . . . . . . . . . . . . . . .
14
Permittivität und Permeabilität . . . . . . . . . . . . . . . . . . . . . . . .
17
1.5.1
18
Relative Permittivität . . . . . . . . . . . . . . . . . . . . . . . . .
2 Plasmonen
2.1
21
Oberflächen Plasmon Polaritonen . . . . . . . . . . . . . . . . . . . . . .
23
2.1.1
23
Dispersionsrelation für SPPs an einer Grenzfläche . . . . . . . . .
3 Anregung von SPPs mit Licht
3.1
3.2
29
Prismenkopplung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
3.1.1
Kretschmann-Konfiguration . . . . . . . . . . . . . . . . . . . . .
30
3.1.2
Otto-Konfiguration . . . . . . . . . . . . . . . . . . . . . . . . . .
32
SPPs an einer Silber/Luft Grenzfläche . . . . . . . . . . . . . . . . . . . .
32
3.2.1
Reflektivität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
3.2.2
Elektromagnetisches Feld . . . . . . . . . . . . . . . . . . . . . .
37
3.2.3
Propagationslänge . . . . . . . . . . . . . . . . . . . . . . . . . .
38
3.2.4
Eindringtiefe . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
3.3
Energietransport durch ein Schichtsystem . . . . . . . . . . . . . . . . .
4 SPP-verstärkte Licht-Molekül-Wechselwirkung
40
43
4.1
Molekulare Anregungen fluoreszenter Moleküle . . . . . . . . . . . . . .
43
4.2
Kopplung zwischen MEs und SPPs . . . . . . . . . . . . . . . . . . . . . .
44
4.3
Starke Kopplung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
4.4
SPP-Molekül-Wechselwirkung . . . . . . . . . . . . . . . . . . . . . . . .
46
4.4.1
Kopplung von SPPs mit Sulforhodamin 101 . . . . . . . . . . . .
47
4.4.2
Oszillatormodell . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
Energietransport durch das Schichtsystem . . . . . . . . . . . . . . . . .
59
4.5
5 Zusammenfassung
63
Anhang
64
A.1 Permittivität der Sulforhodamin 101 Schicht . . . . . . . . . . . . . . . .
65
A.2 Multischichtsystem, Transfermatrixmethode . . . . . . . . . . . . . . . .
67
Literaturverzeichnis
70
-3-
Einleitung
Oberflächen Plasmon Polaritonen (engl. Surface Plasmon Polaritons, SPPs) sind gekoppelte Zustände zwischen elektromagnetischen Feldern und quasi-freien Elektronen in
Metallen, die an die Oberfläche gebunden sind. Sie können unter bestimmten Umständen
an Grenzflächen zwischen Dielektrika und Metallen mit Licht angeregt werden und
da sie sich an Oberflächen ausbreiten, können sie entlang dieser geführt werden. In
Richtung normal zur Oberfläche nimmt die Feldstärke der SPPs exponentiell ab und ist
an der Oberfläche im Vergleich zum anregenden Lichtfeld verstärkt. Die Propagation,
die Streuung, der Energietransfer und die Kopplung von Licht mit Materie sind durch
die Bindung des Lichts an die Oberfläche modifiziert. Neben propagierenden SPPs gibt
es auch lokalisierte Oberflächen Plasmon Polaritonen (engl. Localised Surface Plasmon
Polaritons, LSPs), die durch die Wechselwirkung von Licht und Metallnanopartikeln oder
komplizierteren Nanostrukturen entstehen.
Die spezifischen Eigenschaften von Plasmonen machen diese für Anwendungen in unterschiedlichen Gebieten interessant. So können sie als zweidimensionales Licht in optischen
Schaltkreisen verwendet werden, oder durch ihre evaneszente Natur und ihre extrem
beschränkten Moden-Volumina die Wechselwirkung zwischen Licht und Materie verstärken und so die Empfindlichkeit von optischen Sensoren verstärken. Weiters könnten
sie die Effizienz von organischen Solarzellen erhöhen, indem sie die Lichtabsorption
in der photoaktiven Grenzfläche verstärken. Die Kontrolle von SPPs in plasmonischen
Nanostrukturen führt zu einer Vielzahl von möglichen Anwendungen:
Mit Hilfe der Plasmonik können die Vorteile der Photonik mit den Vorteilen der Elektronik vereint werden. Es wird möglich, die hohe räumliche Konzentrierbarkeit von
Schaltkreisen, die in der Elektronik möglich ist, und die hohen Bandbreiten der Photonik
zu vereinen, sowie das Abbe Limit, das die Miniaturisierung von optischen Schaltkreisen
begrenzt, zu umgehen. SPPs haben aufgrund der Dämpfung im Metall eine beschränkte
Ausbreitungslänge. Für stark miniaturisierte Schaltkreise ist allerdings die erforderliche
Ausbreitungslänge gering41 . Für die Entwicklung von Bauelementen für plasmonische
Schaltungen ist es notwendig, Plasmonen erzeugen zu können, deren Energiefluss man
lenken und fokussieren kann. Die Kombination von Molekülen und SPP-führenden
Elementen könnte zur Entwicklung von plasmonischen Schaltungselementen führen.
Die verstärkte Wechselwirkung von Molekülen mit SPPs wird in der Biochemie, der
Medizin und in vielen anderen Bereichen z.B. in Form der oberflächenverstärkten Raman
Spektroskopie (SERS) angewendet20 .
LSPs und SPPs können zur gezielten Verstärkung und/oder Schwächung der Fluoreszenz
von Molekülen verwendet werden. Das ist in der optischen Sensorik z.B. für Fluoreszenzsensoren sehr relevant und reicht von der Verstärkung des Messsignals von Fluorophoren
durch das verstärkte Nahfeld der SPPs bis zur Detektion einzelner Moleküle über die
Beobachtung der durch die Moleküle veränderte Resonanz von Metallnanopartikeln13 .
Durch die Kopplung von angeregten fluoreszenten Molekülen mit SPP-Moden ist es
möglich, Plasmonenquellen zu erzeugen. Umgekehrt können SPPs durch die Anregung
von fluoreszenten Molekülen wieder in ausbreitungsfähiges Licht verwandelt werden. In
dieser Form kann Information über plasmonische Prozesse gewonnen werden. Licht mit
Hilfe von Molekülen gezielt an SPPs zu koppeln, hat den Vorteil, dass die Anregung von
SPPs durch eine Struktur möglich wird, die sehr klein ist20,21 .
Ein wichtiges Anwendungsgebiet der Plasmonik ist die Steigerung der Effizienz bei
der Gewinnung von Solarenergie. Aufgrund der geringen Ladungsträgermobilität in
organischen Solarzellen müssen diese sehr dünn sein, daher kann nur ein geringer Teil
des Sonnenlichts absorbiert und in Photostrom verwandelt werden. Durch metallische
Nanopartikel in der photoaktiven Zone könnte die Absorption gezielt verstärkt werden.
Eine weitere Steigerung der Effizienz könnte durch die Kontrolle der Lichtstreuung mit
Hilfe von Nanostrukturen erreicht werden13 .
Es ist also von großem Interesse, das Kopplungsverhalten von fluoreszenten Farbstoffmolekülen und SPPs genau zu verstehen. In dieser Arbeit soll das anhand der Kopplung
zwischen SPPs und Sulforhodamin 101 Molekülen untersucht werden.
-5-
Kapitel
1
Grundlagen
1.1 Elektromagnetisches Spektrum
Abbildung 1: Elektromagnetisches Spektrum (xkcd.com/273/)
Das Spektrum des sichtbaren Lichts umfasst den Wellenlängenbereich zwischen 380
und 780 nm, einem Frequenzbereich von circa 3, 8 · 1014 bis 7, 9 · 1014Hz entsprechend.
Angrenzend an das für den Menschen sichtbare Lichtspektrum befindet sich im elektromagnetischen Spektrum der UV-Bereich bei kürzeren und der IR-Bereich bei längeren
Wellenlängen, welche teilweise von anderen Lebewesen wahrgenommen werden können.
1.2 Maxwellgleichungen und elektromagnetische Felder
Elektromagnetische Felder werden durch die Maxwellgleichungen, passende Randbedingungen und konstitutive Relationen vollständig beschrieben6 . Die zeitabhängigen
Maxwellgleichungen kann man als vier lineare Differentialgleichungen wie folgt schreiben:
∇ · D = ρext
(1.1)
∇·B=0
(1.2)
∇×E=−
∇×H=
∂B
∂t
∂D
+ jext
∂t
(1.3)
.
(1.4)
E ist die elektrische Feldstärke, D ist die dielektrische Verschiebung, B ist die magnetische
Flussdichte oder Induktion und H ist die magnetische Feldstärke.
ρext und jext sind
die externe Ladungsdichte und die externe Stromdichte. Die konstitutiven Materialgleichungen beschreiben die mikroskopische Reaktion der Materie auf elektromagnetische
Strahlung. Für lineare isotrope Medien lauten sie:
D = ϵ0 E + P = ϵ0 (1 + χe )E = ϵ0εr E
(1.5)
B = µ 0 H + M = µ 0 (1 + χm )H = µ 0 µr H,
(1.6)
wobei χe die elektrische und χm die magnetische Suszeptibilität ist. Die vier makroskopischen Felder sind in den Materialgleichungen über P und M verknüpft. P und M sind
die elektrische und die magnetische Polarisation. ϵ0 ist die Permittivität des Vakuums,
µ 0 die Permeabilität des Vakuums, εr ist die relative Permittivität und µr die relative
Permeabilität23 .
In der Elektrodynamik wird üblicherweise zwischen gebundenen und freien Ladungsund Stromdichten in Materialien unterschieden. Frei bezieht sich darauf, dass die Größen mit den relativ mobilen Leitungselektronen assoziiert werden können, während die
gebundenen Größen durch Effekte der stark an ihre Atome oder Moleküle gebundenen
Elektronen entstehen.
In der Literatur zur Plasmonik wird jedoch oft die hier gewählte Unterscheidung getroffen
- die, zwischen internen und externen Ladungs- und Stromdichten. Die Ladungen und
-7-
Ströme des externen Sets kommen aus Quellen außerhalb des Systems, das beschrieben
wird. Die Ladungen und Ströme des internen Sets sind mit den Leitungselektronen und
den gebundenen Elektronen innerhalb des Systems assoziiert. Die internen Ladungs- und
Stromdichten sind ρ und j. Die gesamte Ladungsdichte und die gesamte Stromdichte
sind23,25,43 :
ρtot = ρext + ρ
(1.7)
jtot = jext + j.
(1.8)
Die Quellen des elektromagnetischen Feldes sind freie Ladungen und Ströme. Für die
meisten Phänomene in der Optik wird ein Bereich betrachtet, in dem das elektromagnetische Feld des Lichts von seinen Quellen entkoppelt ist. Wird ein System von außen durch
ein solches elektromagnetisches Feld angeregt, sind ρext = 0 und jext = 0. Für ρext = 0
und jext = 0 werden die Maxwellgleichungen homogen. Viele in der Optik verwendete
Materialien haben weder Ladungsquellen noch Senken, d.h. auch ρ = 0. Wir erhalten
dann24 :
∇·D=0
(1.9)
∇·B=0
(1.10)
∂B
∂t
(1.11)
∂D
.
∂t
(1.12)
∇×E=−
∇×H=
-8-
1.3 Wellengleichung
Bildet man die Rotation der dritten und der vierten homogenen Maxwellgleichung und
verwendet die Identität ∇ × ∇ × E = ∇(∇ · E) − ∇2 E, bekommt man unter der Annahme
homogener Medien, für die auch gilt ∇εE = ε∇E,
∂E2
∇ E − ∇(∇ · E) − ϵ0 µ 0εr µr 2 = 0.
∂t
2
Eine ähnliche Gleichung gilt für H, daraus ergeben sich die zwei transversalen Wellengleichungen
∇2 E − ε 0 µ 0ϵr µr
∂E2
=0
∂t 2
∇2 H − ε 0 µ 0ϵr µr
∂H2
= 0.
∂t 2
Die räumliche und die zeitliche Abhängigkeit kann separiert werden. Wählt man als
Lösungen Felder mit harmonischer Zeitabhängigkeit, ergibt das keine Einschränkung der
Allgemeinheit, da sich aus harmonischen Moden mit Fourier-Analyse jede andere Form
von Zeitabhängigkeit aufbauen lässt17,23 . Die Lösungen haben die Form von monochromatischen Wellen mit Frequenz ω. In komplexer Form kann man sie wie folgt schreiben:
E(r,t ) = E(r)e −iωt . Der Realteil der komplexen Lösung Re (E(r,t )) ist das physikalische
Feld. Im Weiteren wird mit komplexen Lösungen gerechnet; dass die physikalischen
Felder die Realteile der Lösungen sind, wird - außer in Spezialfällen - nicht explizit an√
gegeben. Mit harmonischer Zeitabhängigkeit ergibt sich ∂E
k = ω ϵ 0 µ 0 εr µ r
∂t = −iωE.
ist die Wellenzahl. Für harmonische Felder bekommen die Wellengleichungen folgende
Form:
∇2 E + k 2 E = 0
∇2 H + k 2 H = 0.
Das sind die homogenen Helmholtzgleichungen. Verwendet man fouriertransformierte
Felder E(ω, r), bekommt man aus den Maxwellgleichungen im Frequenzraum die Wellengleichungen sofort in Form der Helmholtzgleichungen und braucht die Einschränkung
auf harmonische Felder nicht zu machen. Die einfachsten Lösungen der Helmholtzgleichungen sind propagierende ebene Wellen.
-9-
E(r,t ) = E0e i (kr−ωt )
H(r,t ) = H0e i (kr−ωt ) .
E0 und H0 sind sind die komplexen Amplituden der Feldstärken. k = kr + iki ist der
komplexe frequenzabhängige Wellenvektor einer propagierenden elektromagnetischen
Welle,
√
|k| = k = ω ϵ0 µ 0εr µr ,
sein Betrag ist die Wellenzahl im Medium.
Die Wellenzahl im Vakuum ist
k0 =
ω 2π
=
.
c
λ
Der Wellenvektor k gibt die Richtung der Phasenbewegung an. Die Phasengeschwindigkeit ist
v=
ω
.
k
Die Phasengeschwindigkeit im Vakuum ist c =
gilt:
√1
ϵ0 µ 0
= 299792458 ms , für andere Medien
c
ω
v=√
= .
εr µ r
k
Die Gruppengeschwindigkeit ist
vд =
dω
.
dk
Sie beschreibt die Geschwindigkeit der Energieausbreitung. In isotropen Medien ist die
Richtung der Gruppengeschwindigkeit gleich der Richtung des Wellenvektors. Ist ω (k )
linear so wie im Vakuum, ω (k ) = ck, dann fallen Phasen- und Gruppengeschwindigkeit
zusammen11 .
- 10 -
1.4 Schichtsystem
In dieser Arbeit werden Schichtsysteme behandelt, auf die unter dem Winkel θi Licht
auf die xy-Ebenen fällt. Im folgenden Abschnitt werden die bei der Berechnung der
elektromagnetischen Felder in einem Schichtsystem verwendeten Annahmen und die bei
den Rechnungen verwendete Notation eingeführt. Die Felder werden in jeder Schicht in
Komponenten zerlegt, die in positive oder negative z-Richtung laufen, um die Propagation
der elektromagnetischen Wellen durch das System zu berechnen. Die Anteile, die sich
in positive z-Richtung bewegen, bekommen hier den Index +; die, die sich in negative
Richtung bewegen den Index -. Wenn die Ausdehnung der Struktur in y-Richtung viel
größer als in z-Richtung ist und es in y-Richtung keine Material- oder Feldvariationen
gibt, gilt ohne Einschränkung der Allgemeinheit E(r ,t ) = E(x,z,t ). Wie schon zuvor
erwähnt, können die räumliche und die zeitliche Abhängigkeit separiert werden. Die
Schichten sind aus isotropen und homogenen Materialien. In diesem Fall werden die
Wellengleichungen zu zwei unabhängigen skalaren Gleichungen. Die Lösungen haben
unterschiedliche Polarisationseigenschaften.
1.4.1 Elektromagnetische Felder im Schichtsystem
z
kt
H+2
E+2
ϴt
ε2
ε1
x
H-1
ϴi
H+1
E-1
ki
kr
E+1
TE
Abbildung 2: Schematische Darstellung der Transmission und Reflexion einer TE-polarisierten elektromagnetischen Welle an einer Grenzfläche. Die Welle wird unter dem Winkel Θi
reflektiert und unter dem Winkel Θt transmittiert.
- 11 -
Für transversal elektrische Wellen, TE-Wellen, gilt: Das elektrische Feld steht normal auf
die Einfallsebene, die xz-Ebene, und hat nur eine y-Komponente, während das magnetische Feld keine y-Komponente hat,
E = (0,Ey , 0)(x,z)e −iωt
(1.13)
H = (Hx , 0,Hz )(x,z)e −iωt .
(1.14)
z
kt
E+2
H+2
ϴt
ε2
ε1
x
E-1
ϴi
E+1
H-1
ki
kr
H+1
TE
Abbildung 3: Schematische Darstellung der Transmission und Reflexion einer TM-polarisierten
elektromagnetischen Welle an einer Grenzfläche. Die Welle wird unter dem Winkel Θi
reflektiert und unter dem Winkel Θt transmittiert.
Für transversal magnetische Wellen, TM-Wellen, gilt: Das magnetische Feld steht normal
auf die Ebene, auf die das Licht einfällt und hat nur eine y-Komponente, während das
elektrische Feld keine y-Komponente hat,
H = (0,Hy , 0)(x,z)e −iωt
(1.15)
E = (Ex , 0,Ez )(x,z)e −iωt .
(1.16)
Es ergeben sich die zwei folgenden skalaren Helmholtzgleichungen:
Für TE-Wellen
(
∂2
∂ 1 ∂ ω2
+
µ
(z)
+ εr µr )Ey (x,z) = 0,
∂x 2
∂z µr (z) ∂z c 2
- 12 -
(1.17)
für TM-Wellen
∂2
∂ 1 ∂ ω2
( 2 + εr (z)
+ εr µr )Hy (x,z) = 0.
∂x
∂z εr (z) ∂z c 2
(1.18)
Die verschiedenen Lagen sind in z-Richtung aufgeschichtet, klz ändert sich für jede Schicht
l an jeder Grenzfläche. kx ist ein Parameter, der durch den Einfallswinkel bestimmt wird,
daher können die x-abhängigen Anteile separiert werden:
E (x,z) = E (z)e ±ikx x
H (x,z) = H (z)e ±ikx x .
(1.19)
Die Helmholtzgleichungen werden zu gewöhnlichen Differentialgleichungen:
∂ 1 ∂ ω2
+ εr µr − kx2 )Ey (z) = 0
∂z µr (z) ∂z c 2
(1.20)
∂ 1 ∂ ω2
+ εr µr − kx2 )Hy (z) = 0.
∂z εr (z) ∂z c 2
(1.21)
(µr (z)
(εr (z)
Die Lösung der Helmholtzgleichung für TE-polarisiertes Licht kann wie folgt geschrieben
werden:
Eyl (z) = E +l e ikl z (z−z+l 0 ) + E −l e −ikl z (z−z −l 0 ) .
(1.22)
Die Lösung der Helmholtzgleichung für TM-polarisiertes Licht kann wie folgt geschrieben
werden:
Hyl (z) = H +l e ikl z (z−z+l 0 ) + H −l e −ikl z (z−z −l 0 ) .
(1.23)
Die Tangentialkomponenten der Felder müssen an den Grenzflächen der Schichten stetig
sein. Das bedeutet
für TE-Wellen
Eyl (z) = Eyl+1 (z)
Hxl (z) = Hxl+1 (z)
(1.24)
Hyl (z) = Hyl+1 (z)
Exl (z) = Exl+1 (z).
(1.25)
und für TM-Wellen
Die in dieser Arbeit untersuchten Schichtsysteme werden mit TM-polarisiertem weißen
Licht bestrahlt. Daher werden im Weiteren nur die Feldkomponenten für TM-polarisiertes
Licht genauer behandelt. Für harmonische Felder gilt:
∇ × H = −iωD.
- 13 -
Aus der y-Komponente des magnetischen Feldes erhält man damit das TM-polarisierte
elektrische Feld:
−
kx
(H +l e ikl z (z−z+l 0 ) + H −l e −ikl z (z−z −l 0 ) )
ϵ 0 εl ω
(1.26)
kz l
(H +l e ikl z (z−z+l0 ) − H −l e −ikl z (z−z −l 0 ) ).
ϵ 0 εl ω
(1.27)
Ezl (z) = −
Exl (z) =
1
∇×H=E
iωϵ0εr
Daraus sieht man, dass die Randbedingungen für TM-polarisiertes Licht an den Grenzflächen auch wie folgt geschrieben werden können24 :
1 ∂Hl (zl )
1 ∂Hl+1 (zl )
=
.
εl ∂z
εl+1
∂z
Hl (zl ) = Hl+1 (zl )
(1.28)
Die Randbedingungen führen zu einem System von Gleichungen, mit dem die Reflektivität,
die Transmittivität und die elektromagnetischen Felder im Schichtsystem berechnet
werden können (siehe Anhang A.2). Der y-Index wird fallen gelassen; falls nicht anders
gekennzeichnet, handelt es sich im Weiteren um die y-Komponente des Magnetfeldes.
1.4.2 Fresnelkoeffizienten, Reflektivität und Transmittivität
eines N-Schichtsystems
A
B
C
D
E
...
0
1
2
...
N
N+1
Abbildung 4: Schematische Darstellung der Reflexion und Transmission in einem N-Schichtsystem:
Gezeigt sind die ersten Ordnungen der Reflexion an der ersten Grenzschicht1 .
Trifft Licht auf eine dünne Schicht, tritt in der Schicht eine unendliche Anzahl interner
Reflexionen auf. In einem N-Schichtsystem tritt in jeder Schicht eine unendliche Anzahl interner Reflexionen auf. Das Verhältnis zwischen einfallendem und reflektiertem
- 14 -
elektromagnetischen Feld ist der Reflexionskoeffizient. Für TM-polarisiertes Licht gilt:
rT M =
Hre f
.
Hinc
(1.29)
Die Reflektivität, das Verhältnis zwischen einfallender und reflektierter Intensität, ist:
RT M (ω,θ ) = |rT M | 2 .
(1.30)
θ ist der Winkel, mit dem das Licht auf das Schichtsystem trifft. Der Transmissionskoeffizient ist das Verhältnis zwischen einfallendem und transmittiertem elektromagnetischen
Feld,
tT M =
Htrans
.
Hinc
(1.31)
Die Transmittivität, das Verhältnis zwischen Input und Output der Intensität, ist:
TT M (ω,θ ) =
nn+1 cos θn+1 |tT M | 2
.
n 0 cos θ 0
(1.32)
Mit dem Gesetz von Snellius, nn sin θn = nn+1 sin θn+1 , erhält man die Einfallswinkel in
die jeweilige Schicht. Die Absorption kann über die Energieerhaltung definiert werden,
A = 1 − R(ω,θ ) − T (ω,θ ).
(1.33)
Um die Reflektivität bzw. Transmittivität eines N-Schichtsystems zu erhalten, berechnet
man zuerst die Reflexions- bzw. Transmissionskoeffizienten eines Systems mit einer einzigen Grenzfläche zwischen zwei Medien, die Fresnelkoeffizienten. Sie ergeben sich aus den
Randbedingungen für die elektromagnetischen Felder. Für die Tangentialkomponenten
des elektrischen Feldes Ex (z) und die Tangentialkomponenten des magnetischen Feldes
Hy (z) in TM-Polarisation erhält man an der Grenzfläche, die im gewählten Bezugssystem
bei z = 0 liegt, für die Tangentialkomponenten des magnetischen Feldes
H +0 + H −0 = H +1
(1.34)
und für die Tangentialkomponenten des elektrischen Feldes
k 0z
k 1z
(H +0 − H −0 ) =
(H +1 ).
ε0
ε1
- 15 -
(1.35)
z
ε
x
ε
k
Abbildung 5: Grenzfläche zwischen zwei Medien, auf die eine elektromagnetische Welle mit Wellenvektor k trifft.
Aus dem zweiten Medium gibt es im Fall einer einzigen Grenzfläche keine einfallende
Welle, H −1e ik1z (z−z10 ) = 0. Für ein System mit einer Grenzfläche erhält man aus 1.34 und
1.35 die Fresnelkoeffizienten: Der Reflexions- und der Transmissionskoeffizient sind
r 01 =
H −y0 kz0ε 1 − kz0ε 1
=
H +y0
kz0ε 1 + kz1ε 0
(1.36)
t 01 =
H +y1
2kz0ε 1
=
.
H +y0 kz0ε 1 + kz1ε 0
(1.37)
und
Reflektivität einer Schicht
Es wird eine Struktur mit zwei Grenzflächen und der Schichtdicke d betrachtet. Trifft eine
ebene Welle mit der Amplitude A auf die erste Grenzfläche, wird sie in erster Ordnung
mit B = r 01A reflektiert, und mit t 01A transmittiert. Das Licht, das von der anderen Seite
der ersten Grenzfläche transmittiert wird, hat den Transmissionskoeffizienten t 10 . In der
Schicht ändert sich die Phase um δϕ = kz1d. Der Reflexionskoeffizient an der zweiten
Grenzfläche ist r 12 . Die Reflexionen höherer Ordnung sind:
C = t 10t 01r 12 exp(2ikz1d )A,
2
D = t 10t 01r 01r 12
exp(4ikz1d )A
(1.38)
und die jte-Partialwelle ist:
j j−1
P j = t 10t 01r 12
r 10 exp(2jikz1d )A.
(1.39)
Die an der Schicht reflektierte Welle ist die Summe aller j-Beiträge:
rslab A = B + C + D . . . = [r 01 + t 10t 01r 12
- 16 -
X
j j
r 12
r 10 exp(2jikz1d )]A.
(1.40)
Die Summe reflektierter Ordnungen kann als Summe einer geometrischen Reihe geschrieben werden. Mit q = r 12r 10 exp(2ikz1d ) erhält man für den Reflexionskoeffizienten der
Schicht folgenden Ausdruck:
r 0,1slab = r 01 + (t 10t 01r 12 exp(2jikz1d )
Verwendet man
P
qj =
1
1−q ,
X
qj .
(1.41)
erhält man:
r 0,1slab = r 01 +
t 10t 01r 12 exp(2ikz1d )
.
1 − r 12r 10 exp(2ikz1d ))
(1.42)
Mit tij t ji = 1 − rij2 und rij = −r ji ergibt sich:
r 0,1slab =
r 01 + r 12 exp(2ikz1d )
1 + r 12r 01 exp(2ikz1d )
(1.43)
t 0,1slab =
t 01t 12 exp(ikz1d )
.
1 + r 01r 12 exp(2ikz1d )
(1.44)
und
Für ein N-Schichtsystem kann man mit der oben für rslab gefundenen Formel für eine
Schicht den Reflexionskoeffizienten aller N-Schichten berechnen, indem man diese rekursiv anwendet1 .
An der N-ten Grenzfläche gilt, da von rechts keine Welle einfällt, r N −1,N slab = r N −1,N . Für
alle weiteren Schichten gilt:
ri,i+1slab =
ri,i+1 + ri+1,i+2slab exp(2ikzi+1di+1 − di )
.
1 + ri,i+1ri+1,i+2 exp(2iki+1zdi+1 − di)
(1.45)
1.5 Permittivität und Permeabilität
Die Permittivität ist ε = ϵ0εr , die Permeabilität µ = µ 0 µr . Um die optischen Eigenschaften
von Materialien zu beschreiben, werden im Allgemeinen drei Größen verwendet: Die
komplexe relative Permittivität εr , die die Reaktion des Materials auf die durch das
elektrische Feld erzeugte Polarisation beschreibt, die komplexe relative magnetische
Permeabilität µr , die Reaktion auf die durch das magnetische Feld erzeugte magnetische
Polarisation, und der komplexe Brechungsindex n. Diese drei Größen sind wie folgt
miteinander verknüpft29 :
n=
r
εµ
√
= εr µ r .
ϵ0 µ 0
(1.46)
As
Die Permittivität des Vakuums ist ϵ0 = 8.8510−12 Vm
, die Permeabilität des Vakuums ist
Vs
µ 0 = 4π 10−7 Am
V s. Die relative Permittivität oder dielektrische Funktion ist material-
abhängig und dimensionslos, genauso wie die relative magnetische Permeabilität. Für
- 17 -
anisotrope Materialien sind relative Permittivität und relative Permeabilität Tensoren.
Für isotrope Materialien werden die beiden Größen zu Skalaren. Für Frequenzbereiche,
in denen das zu beschreibende Material nicht absorbiert, werden relative Pemittivität,
relative Permeablität und Brechungsindex zu reellen Größen. In dieser Arbeit werden
ausschließlich nicht magnetische Materialien verwendet. Für nicht magnetische Materialien ist µr = 1. Im Allgemeinen sind die optischen Parameter jedoch frequenzabhängig.
Die Veränderung der optischen Parameter als Funktion der Frequenz wird als Dispersion
bezeichnet. Fast alle Medien verursachen Dispersion, nur im Vakuum und für kleine Frequenzbereiche ist die Ausbreitung von elektromagnetischen Wellen frequenzunabhängig.
1.5.1 Relative Permittivität
In diesem Abschnitt werden zuerst das Lorentz- und das Drude-Modell eingeführt. Darauf
folgend wird mit Hilfe des Drude-Modells die relative Permittivität oder dielektrische
Funktion eines idealen Metalls berechnet.
Um die relative Permittivität von Materialien phänomenologisch zu beschreiben, wird das
klassische Modell von Hendrik Antoon Lorentz verwendet. Im Lorentz-Modell verwendet
man den klassischen harmonischen Oszillator, um die Polarisation, die durch das elektrische Feld induziert wird, zu berechnen. Um die mikroskopische Reaktion des Materials
auf elektromagnetische Strahlung zu beschreiben, betrachtet man Atome oder Moleküle
als unabhängige, gebundene, gedämpfte und harmonische Oszillatoren, deren Elektronen
durch ein harmonisches elektromagnetisches Feld relativ zum Ionenrumpf ausgelenkt
werden. Die Coulombanziehung wirkt als Rückstellkraft zwischen Elektronen und Ionenrümpfen, die die Elektronen in ihre Gleichgewichtsposition zurück zieht und so entsteht
ein oszillierender Dipol29 . Die Stärke der Rückstellkraft ist dabei proportional zu einer
Federkonstante κ f , die so gewählt wird, dass sie mit der natürlichen Resonanzfrequenz
q
κ
ω0 = mfr des Atoms zusammen passt, bzw. mehrere Federkonstanten, die mit den natürlichen Resonanzfrequenzen ωi des Atoms oder Moleküls zusammen passen. Realistische
optische Medien haben viele Resonanzfrequenzen, d.h. elektronische Oszillatoren in verschiedenen Frequenzbereichen10 . mr ist die reduzierte Masse von Atomkern und Elektron.
Da die Wechselwirkung zwischen Metallen und elektromagnetischer Strahlung im sichtbaren Bereich hauptsächlich vom Verhalten der quasi-freien Leitungselektronen abhängt,
und die Leitungselektronen die Rückstellkräfte der Metallionenrümpfe kaum spüren,
kann man zur Berechnung der dielektrischen Funktion von Metallen das Lorentz-Modell
zum Drude-Modell vereinfachen. In diesem Modell gibt es keine Rückstellkräfte. Die
Stoßprozesse der Elektronen mit Ionenrümpfen und Defekten gehen wie beim LorentzModell als Reibungskraft bzw. Dämpfung in die Gleichung ein26 .
- 18 -
Die Bewegungsgleichungen für ein Elektron in einem harmonischen elektromagnetischen
Feld sind:
Im Lorentz-Modell
me
d 2 x(t )
dx(t )
+ me γ
+ me ω 02 x(t ) = −eE(t )
2
d t
dt
(1.47)
dx(t )
d 2 x(t )
+ me γ
= −eE(t ).
2
d t
dt
(1.48)
und im Drude-Modell
me
e ist die Ladung, me die effektive Masse, ω die Frequenz und E die elektrische Feldstärke
des externen elektromagnetischen Felds. Die Dämpfung ist gegeben durch γ = 1/τ , wobei
τ die mittlere Relaxationszeit des freien Elektronengases ist23 .
Löst man die mit dem Drude-Modell gefundene Bewegungsgleichung für ein Elektron
in einem harmonischen elektromagnetischen Feld mit dem Ansatz E(t ) = E0e −iωt und
x(t ) = x0e −iωt , so erhält man
x(t ) =
me
e
E0e −iωt .
+ iγ ω)
(1.49)
(ω 2
Aus der Auslenkung des Elektrons x(t ) ergibt sich das Dipolmoment
p(t ) = −ex(t )
(1.50)
und daraus mit N, der Anzahl der Oszillatoren pro Einheits-Volumen, die Polarisation
P = N p.
(1.51)
Aus der Polarisation kann unter Verwendung von 1.5 die dielektrische Funktion wie folgt
berechnet werden:
N e2
E
me (ω 2 + iγ ω)
(1.52)
N e2
)E.
me (ω 2 + iγ ω)
(1.53)
P = −N ex = −
ϵ0εr E = ϵ0 (1 −
ωp ist die natürliche Resonanzfrequenz der Elektronen ωp2 =
N e2
ϵ0me .
Die dielektrische Funktion (des quasi-freien-Elektronen-Modells) ist:
εr (ω) = ε 0 + iε 00 = 1 −
- 19 -
ωp2
ω 2 + iγ ω
(1.54)
εr (ω) = 1 −
ωp2
ω2 + γ 2
+i
ωp2γ
ω (ω 2 + γ 2 )
.
(1.55)
Der Imaginärteil modelliert den mikroskopischen Prozess der Absorption des Materials.
Bei geringer Dämpfung, ω γ , vereinfacht sich der Ausdruck der dielektrischen Funktion
zu:
εr (ω) = ε + iε = 1 −
0
00
ωp2
ω2
+i
ωp2γ
ω3
.
(1.56)
Das Drude-Modell ist für viele Metalle bei Frequenzen im Bereich des sichtbaren Lichts
sowie im infraroten Bereich des Spektrums eine gute Näherung29 . Vergleicht man das
Drude-Modell mit experimentellen Daten, sieht man, dass das Modell für Edelmetalle
noch modifiziert werden muss. Das gefüllte d-Band bei Cu, Au und Ag verursacht in
Kombination mit dem positiven Hintergrund des Ionengitters eine stark polarisierte
Umgebung. Dieser Effekt geht über die dielektrische Konstante ε ∞ in die dielektrische
Funktion ein. Ihr Wert liegt zwischen 1 und 1011,23 . Für Frequenzen im Ultravioletten
Bereich müssen Beiträge von Interbandübergängen der gebundenen Elektronen beachtet
werden32 . Um die durch die Bandübergänge erzeugte Polarisation zu berechnen, wird dem
Drude-Modell ein Lorentzoszillatorterm hinzugefügt. Auch für direkte Bandübergänge
in Halbleitern kann man Lorentzoszillatorterme verwenden23 .
In den in dieser Arbeit untersuchten Beispielen wird zur Berechnung der dielektrischen
Funktion von Silber ein nur durch die dielektrische Konstante ε ∞ modifiziertes DrudeModell verwendet.
- 20 -
Kapitel
2
Plasmonen
Aufgrund der Ähnlichkeit der Dynamik der Leitungselektronen in Metallen und der
Bewegung von geladenen Ionen in einem Plasma kann man die Leitungselektronen eines
Metalls als Plasma auffassen27 . Wie man sehen wird, sind in Plasmen und in Metallen
kollektive Ladungsdichteoszillationen möglich, die sich wellenartig ausbreiten können.
Quantisiert man diese Plasmaoszillationen, bekommt man ein Quasiteilchen, das Plasmon.
Plasmonen sind Bosonen, folgen also der Bose-Einstein-Statistik.
Für den vereinfachten Ausdruck der dielektrischen Funktion von Metallen
εr (ω) = 1 −
ωp2
ω2
(2.1)
wird an der Stelle ω = ωp die dielektrischen Funktion εr (ω) = 0.
Wie aus den folgenden Ausführungen ersichtlich werden wird, führt das zu einem interessanten Resultat. Aus der Wellengleichung im Fourierraum sieht man, dass eigentlich
zwei Arten von Wellen möglich sein müssten, transversale und longitudinale:
k(k · E) − k 2 E + εr (ω)
ω2
E = 0.
c2
(2.2)
In Abwesenheit äußerer Ladung gilt mit dem Gaußschen Gesetz:
∇ · D = ∇ε · E = 0.
(2.3)
Ist ∇ · E = 0, sind nur transversale Felder möglich. Das Gaußsche Gesetz scheint also
zuerst longitudinale Moden auszuschließen. Ohne Dämpfung wird bei ω = ωp die relative
Permittivität jedoch Null, daraus folgt εr (ω) ωc 2 E = 0. ∇ · E =
2
ρ t ot
ϵ0 ,
d.h. longitudinale
Moden werden möglich. Aus
D = ϵ0 E + P = 0
(2.4)
sieht man, dass die longitudinalen Felder bei ωp durch ein Depolarisationsfeld E =
−P
ϵ0
im
Plasma entstehen. Wird auch die Dämpfung in der dielektrischen Funktion berücksichtigt,
dann geschieht das genau bei all jenen Frequenzen, für die die dielektrische Funktion Null
wird. Das gesamte Plasma schwingt mit derselben Frequenz, alle Elektronen bewegen
sich in Phase. Das Quasiteilchen dieser Plasmaoszillation mit E = ~ωp heißt Volumsoder Bulkplasmon, ωp nennt man auch die Volumsplasmafrequenz. Da Licht ebener
Wellen rein transversalen Charakter hat, Volumsplasmonen hingegen rein longitudinalen
Charakter haben, können Volumsplasmonen nicht einfach mit Licht angeregt werden.
Man kann sie aber mit schnellen Elektronen anregen26 .
Aus k · E = 0 für transversale Wellen ergibt sich aus 2.2, mit εr (ω) = 1 −
ωp2
,
ω2
folgende
Dispersionsrelation:
ω 2 = c 2k 2 + ωp2 .
(2.5)
Für ω > ωp sind propagierende transversale elektromagnetische Wellen möglich, für
ω < ωp nicht. Ab ω = ωp beginnen Metalle transparent zu werden, da bei ω > ωp
und ε > 0 die Elektronen auf das einfallende elektromagnetische Feld, und das dadurch
erzeugte Ladungsungleichgewicht, nicht mehr schnell genug reagieren können. Das
transversale elektromagnetische Feld kann propagieren. Für ω < ωp und ε < 0 hingegen
wird das elektromagnetische Feld von den Elektronen abgeschirmt und fällt im Metall
exponentiell ab. Das sind keine ebenen elektromagnetischen Wellen mehr, sondern
sogenannte evaneszente Lösungen der Wellengleichung. Daher sind Metalle auch hoch
reflektierend im Bereich des sichtbaren Lichts und durchsichtig im Ultravioletten. An den
Oberflächen von Metallen wird die Symmetrie gebrochen und es entstehen neue Moden,
sogenannte Oberflächenplasmonen. Die Negativität der dielektrischen Funktion ist für
die im Folgenden untersuchten Oberflächenplasmonen notwendig27,29,48 .
- 22 -
2.1 Oberflächen Plasmon Polaritonen
Plasmonen - kollektive, resonante, longitudinale Ladungsdichteoszillationen in Metallen
oder anderen Plasmen - treten nicht nur in Metallen, sondern auch an Grenzflächen
zwischen Metallen und Dielektrika auf. Das Quasiteilchen dieser Oszillation ist das Oberflächenplasmon, im Englischen Surface Plasmon (SP). Diese an die Oberfläche gebundenen
Ladungsdichte-Oszillationen haben an einer Grenzfläche zwischen Luft (εd = 1) und
einem Metall mit der dielektrischen Funktion 2.1 eine Eigenfrequenz von
ωp
ωp
ωsp = √
=√ .
1 + εd
2
(2.6)
0 5 ω (kx ) < ωsp
(2.7)
Für Frequenzen zwischen
können propagierende Plasmonwellen angeregt werden, die entlang der Grenzfläche
zwischen Metallen und Dielektrika propagieren, während ihre Amplituden normal zur
Oberfläche exponentiell abfallen, d.h sie sind an die Oberfläche gebunden. Sie werden als
Oberflächen Plasmon Polaritonen, im Englischen als Surface Plasmon Polaritions (SPPs)
bezeichnet. SPPs entstehen durch die Kopplung zwischen oszillierenden Leitungselektronen an der Oberfläche von Metallen und elektromagnetischen Wellen32 . Als Polaritonen
bezeichnet man Quasiteilchen, die durch starke Kopplung zwischen elektromagnetischen Feldern und elektromagnetischen Anregungen, die ein Dipolmoment besitzen,
entstehen49 . Die SPs sind der elektrostatische Grenzfall der SPPs, sie propagieren nicht.
Wenn die Wellenzahl der SPPs, kSPPx , gegen unendlich geht, geht die Gruppengeschwindigkeit der Oberflächenwellen gegen Null. In der Literatur werden SPP und SP allerdings
oft synonym verwendet16,23 .
2.1.1 Dispersionsrelation für SPPs an einer Grenzfläche
Um die grundlegenden Eigenschaften von SPPs einzuführen, wird zuerst eine Grenzfläche
zwischen zwei semiunendlichen Halbräumen, bestehend aus einem Dielektrikum und einem Metall, betrachtet. Auf diese Grenzfläche fällt unter einem Winkel θi von der Seite des
Dielektrikums Licht. Alle im Weiteren in dieser Arbeit betrachteten Materialien werden
als nicht magnetisch angenommen. Der Effekt, den die Diskontinuität von Materialeigenschaften an einer Grenzfläche auf ein einfallendes elektromagnetisches Feld hat, wird
daher allein durch die dielektrische Funktion εr (ω) bestimmt. Die Normalkomponente
des dielektrischen Verschiebungsfeldes D muss über die Grenzfläche hinweg stetig sein.
Aus ϵ0εr E = D sieht man: Wenn εr an der Grenzfläche sein Vorzeichen wechselt, muss
auch die Normalkomponente des elektrischen Feldes ihr Vorzeichen - d.h. ihre Richtung ändern. Zeigt das elektrische Feld von der Grenzfläche weg, sammeln sich Elektronen an
der Grenzfläche; zeigt es zur Grenzfläche, sammelt sich positive Ladung an der Grenz-
- 23 -
fläche. Das führt zur Ladungspolarisation. Ist das elektrische Feld zeitlich veränderlich
und harmonisch, ist es auch die durch das elektrische Feld induzierte Ladungspolarisation. Damit SPP-Moden möglich werden, ist die Negativität der dielektrischen Funktion
des Metalls also notwendig11,29 . Das einfallende Licht muss eine elektrische Normalkomponente haben, damit die Anregung von SPPs möglich ist. Transversal magnetisch
polarisiertes Licht hat eine elektrische Normalkomponente, TE-polarisiertes Licht nicht.
TM-polarisiertes Licht kann also Ladungspolarisationsoszillationen erzeugen29 . Stimmen
der Wellenvektor und die Frequenz des einfallenden Lichts mit dem Wellenvektor und
der Frequenz der SPP-Mode überein, kann das Licht an diese Mode koppeln und eine
propagierende Oberflächenwelle anregen. Das SPP ist ein Hybridzustand, der durch die
Kopplung zwischen einfallendem elektromagnetischen Feld und Plasmonen entsteht. Um
die Parameter zu finden, unter denen eine solche Kopplung möglich ist, muss man den
Zusammenhang zwischen Wellenvektor k und Kreisfequenz ω, die Dispersionsrelation,
betrachten.
TM-polarisiertes Licht fällt vom Dielektrikum mit Permittivität εd auf das Metall mit
Permittivität εm . Das einfallende Feld erzeugt ein reflektiertes Feld in z < 0 und ein
transmittiertes Feld in z > 0. Aus den Helmholtzgleichungen für TM-polarisiertes Licht
erhält man die reflektierten Felder
Ed = (Exd , 0,Ezd )e i (−kzd z+kx x −ωt )
(2.8)
Hd = (0,Hyd , 0)e i (−kzd z+kx x −ωt ) ,
(2.9)
und die transmittierten Felder
Em = (Exm , 0,Ezm )e i (kzm z+kx x −ωt )
(2.10)
Hm = (0,Hym , 0)e i (kzm z+kx x −ωt ) .
(2.11)
Das einfallende Feld wird Null gesetzt, um die hier gesuchte Eigenwertgleichung zu
bekommen. Die Wellen bewegen sich in der xy-Ebene in die x-Richtung, und sind in
y-Richtung invariant, daher kann ky ohne Einschränkung der Allgemeinheit Null gesetzt
√
werden. Die Wellenzahl im jeweiligen Medium ist definiert als ki = ωc εi . Teilt man den
Wellenvektor in Normal- und Tangentialkomponenten, ergibt sich
ω
ki 2 = ( ) 2εi = kx 2 + kzi 2 .
c
- 24 -
(2.12)
Da sich die Medien entlang der Grenzfläche in x-Richtung nicht ändern, besteht kontinuierliche Translationssymmetrie in x-Richtung, die x-Komponente des Wellenvektors ist
also eine erhaltene Größe und es gilt17 :
kxd = kxm = kx .
(2.13)
εd ist die dielektrische Funktion des Dielektrikums, εm ist die dielektrische Funktion des
Metalls. In z-Richtung gilt:
r
q
ω
ω2
2
εd 2 − kx =
εd − εd sin2 θi
c
c
kzd =
r
kzm =
εm
q
ω2
2 = ω ε − ε sin2 θ .
−
k
m
i
d
x
c2
c
(2.14)
(2.15)
Es gelten die Maxwellgleichungen und die dazugehörigen Randbedingungen. Aus den
Stetigkeitsbedingungen an den Grenzflächen
Exd = Exm
Hyd = Hym
(2.16)
erhält man unter Verwendung von
∇ × H = ϵ 0 εr
∂E
∂t
(2.17)
bei harmonischer Zeitabhängigkeit für die reflektierten Felder:
− ikzd Hyd = iωϵ0εd Exd ,
(2.18)
und für die transmittierten Felder:
ikzm Hym = iωϵ0εm Exm .
- 25 -
(2.19)
Daraus folgen die Gleichungen:
Hym
kzd
kzm
+ Hyd
=0
εm
εd
(2.20)
Hym − Hyd = 0,
(2.21)
woraus sich folgender Zusammenhang zwischen den dielektrischen Funktionen und den
Normalkomponenten der Wellenvektoren ergibt:
kzd kzm
+
= 0.
εd
εm
(2.22)
Unter Verwendung von 2.14 und 2.15 erhält man schließlich den expliziten analytischen
Ausdruck für die x-Komponete des Wellenvektors der SPPs:
kSPPx
ω
=
c
r
εd εm
.
εd + εm
(2.23)
Das ist die Dispersionsrelation für SPPs an der Grenzfläche zwischen zwei semiunendlichen Medien und die Bedingung für die Anregung der Eigenmode des Systems, der
SPP-Mode. Wie zuvor beschrieben, treten SPPs bei Frequenzen auf, bei denen sich das
Vorzeichen von εr an der Grenzfläche ändert. Es gilt also:
εd εm < 0.
(2.24)
Ist eines der Materialien ein reines Dielektrikum, gilt für die Permittivität des Dielektrikums im betrachteten Frequenzbereich:
00
0
εd = 0
εd > 0.
(2.25)
Für Metall gilt:
0
0
εm < 0
0
00
|εm | εm .
(2.26)
00
kSPPx = kSPPx + ikSPPx ist eine komplexe Größe. Damit eine propagierende Welle in
x-Richtung existieren kann, muss kSPPx einen Realteil haben. Damit das zutrifft, muss
0
|εm | > εd
(2.27)
gelten. Mit diesen Bedingungen für die Komponenten der εi findet man folgende Ausdrücke: Für den Realteil
0
kSPPx
ω
=
c
s
- 26 -
εm εd
0
εm + εd
0
(2.28)
und für den Imaginärteil
0
00
kSPPx
ω εm εd
=
c εm0 + εd
! 32
00
εm
0 .
2εm2
(2.29)
Betrachtet man den Realteil, sieht man aus den oben gefundenen Bedingungen 2.24 - 2.27,
dass die Tangentialkomponente des Wellenvektors des einfallenden Lichts immer kleiner
0
als kSPPx ist. Der maximal mögliche Wellenvektor, den Licht in einem Dielektrikum
√
in x-Richtung haben kann, ist kxd = ωc εd und heißt Lichtlinie. Die Lichtlinie und die
Tangentialkomponente des Wellenvektors der SPPs haben also keinen Schnittpunkt. Aus
den oben gefundenen Bedingungen sieht man auch, dass die Normalkomponente des
Wellenvektors der SPPs,
kSPPzi
ω
=
c
r
εm εd
ω
εi −
=
εm + εd
c
s
εi2
,
εm + εd
(2.30)
in dem Frequenzbereich ω < ωsp , in dem SPPs angeregt werden können, einen Imaginärteil hat, der immer größer 0 und viel größer als der Realteil ist. Die Normalkomponente
des Wellenvektors des einfallenden Lichts spielt für die Kopplung keine Rolle, da, wenn
es einen Realteil gibt, dieser sehr klein ist15,26,29,39 .
Evaneszente elektromagnetische Felder sind dadurch charakterisiert, dass mindestens
eine Komponente des Wellenvektors imaginär ist. Das führt dazu, dass das Feld in diese
Raumrichtung nicht propagiert, es fällt exponentiell ab32 . Unter Vernachlässigung des Realteils der Normalkomponente des SPP-Wellenvektors kann die räumliche Abhängigkeit
des elektrischen Feldes eines SPPs wie folgt geschrieben werden:
e ikS P P x x e −|kS P P z |z .
(2.31)
Zusammenfassend lässt sich sagen: SPPs haben einen transversalen und einen longitudinalen Anteil. Die SPPs sind an die Oberfläche gebunden, ihre elektromagnetischen
Felder haben ein Maximum bei z = 0 und fallen senkrecht zur Oberfläche im jeweiligen
Medium exponentiell ab; der Transversalanteil ist nicht propagierend, er ist evaneszent.
In x-Richtung propagieren die SPPs longitudinal entlang der Grenzfläche. SPPs haben bei
gleicher Frequenz immer größere Impulse als Licht aus einem dielektrischen Medium
mit εd < |εm |.
- 27 -
5
4.5
4
3.5
ω [eV]
3
2.5
2
1.5
ω sp LS
1
k LLLuft
0.5
k SP P LS
0
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
k x [nm −1 ]
Abbildung 1: Die Dispersionsrelation von SPPs an einer Silber/Luft Grenzfläche schneidet sich nicht
mit der Lichtlinie der Luft. Die maximale Photonenergie zur Anregung von SPPs an
einer Silber/Luft Grenzfläche ωsp liegt bei 4.5 eV .
Da die Dispersionsrelation des Lichts keinen Schnittpunkt mit der Dispersionsrelation
der SPPs hat, ist Kopplung zwischen ebenen elektromagnetischen Wellen und SPP-Moden
für dieses System nicht möglich. Energie und Impuls müssen erhalten sein, weil aber
kSPPx > kxd , können keine SPPs angeregt werden. An einer glatten Oberfläche kann Licht
nicht direkt in SPPs koppeln und SPPs sich nicht direkt in Licht umwandeln, sie sind an
die Oberfläche gebunden.
- 28 -
Kapitel
3
Anregung von SPPs mit Licht
Wie man vorher sehen konnte, haben SPPs in einer Struktur mit nur einer glatten Grenzfläche einen tangentialen Wellenvektor, der immer größer ist als der des aus dem Fernfeld
einfallenden Lichtes. Um SPPs optisch anregen zu können, werden verschiedene Methoden verwendet. Dabei geht es immer darum, den Wellenvektor des Lichts zu vergrößern.
Bei der Prismenkopplung wird die Vergrößerung des Photonwellenvektors durch Vergrößerung des Brechungsindex erreicht. Bei der Gitterkopplung wird der fehlende Beitrag
des Photonwellenvektors durch Beugung am Gitter erzeugt. Dafür wird ein Beugungsgitter mit Gitterkonstante a auf der sonst glatten Metalloberfläche erzeugt oder aus einem
dielektrischen Material auf das Metall aufgebracht. Aufgrund der Periodizität des Gitters
sind im k-Raum alle Punkte, die einem Vielfachen des reziproken Gittervektors G =
2π
a
entsprechen, äquivalent. Wird Licht am Gitter gestreut, dann gilt
kn = k + nG
(3.1)
kSPPx = kx + nG
(3.2)
n ist ±1, 2, 3..... .
Wenn die Bedingung
erfüllt ist, kommt es zur Kopplung23 . Das evaneszente Feld der gestreuten Ordnung kann
mit dem evaneszenten Feld des SPPs koppeln.
3.1 Prismenkopplung
Es gibt zwei verschiedene Konfigurationen der Prismenkopplung: Die Otto-Konfiguration
und die Kretschmann-Konfiguration. In den folgenden Modellrechnungen wird die
Kretschmann-Konfiguration verwendet.
3.1.1 Kretschmann-Konfiguration
ϴi
ε1 Glas
ε2 Silber
ε3 Luft
Abbildung 1: Schematische Darstellung der Kretschmann-Konfiguration
Für die Kretschmann-Konfiguration wird durch ein Glasprisma oder einen gläsernen
Halbzylinder eine wenige Nanometer dicke Silber- oder Goldschicht, die auf der anderen
Seite an Luft oder ein anderes Dielektrikum (das einen kleineren Brechungsindex als
Glas hat) grenzt, mit TM-polarisiertem Licht bestrahlt. Mit diesem Schichtsystem ist
es möglich, SPPs optisch anzuregen. Da die Phasengeschwindigkeit des Lichts in Glas
c
ω
√
kleiner ist als in Luft, v = = √ , ist die Wellenzahl im Glas größer, kGlas = ωc ε 1 . Die
k
ε1
Größe der Tangentialkomponente
kGlasx =
ω√
ε 1 sin θi
c
(3.3)
des einfallenden Lichts lässt sich über den Einfallswinkel einstellen, so kann die Größe des Tangentialvektors der SPPs an der Metall-Luft-Grenzfläche erreicht werden,
kSPPx = kGlasx .
Es gilt folgender Zusammenhang zwischen dielektrischer Funktion und komplexem
Brechungsindex:
√
εi = ni + iκ 1
εi0 = ni2 − κi2
- 30 -
εi00 = 2ni κi .
(3.4)
(3.5)
Aus dem Brechungsgesetz von Snellius
sin θt n 1
=
sin θi n 2
(3.6)
folgt: Fällt Licht von einem optisch dichteren in ein optisch dünneres Medium, n 1 >
n 2 , dann wird für große Einfallswinkel sinθt > 1, d.h. θt wird komplex. Brechung ist
nur bis zu einem bestimmten Einfallswinkel möglich, bei diesem Einfallswinkel ist der
Brechungswinkel θt = 90◦ , diesen Einfallswinkel nennt man den kritischen Winkel der
Totalreflexion16 :
θc = arcsin
n2
.
n1
Ist der Einfallswinkel größer als der kritische Winkel der Totalreflektion, wird kx >
(3.7)
ω√
c ε2.
Für reelle Brechungsindizes wird die z-Komponente des transmittierten Wellenvektors
im zweiten Medium imaginär; die Tangentialkomponente des Wellenvektors wird zu
groß, um im zweiten Medium eine propagierende Welle zuzulassen. (Für komplexe
Brechungsindizes hat die z-Komponente des transmittierten Wellenvektors kz2 im zweiten
Medium einen Imaginär- und einen kleinen Realteil):
kz2 =
ωp
ε 2 − ε 1 sin θi .
c
(3.8)
Fällt Licht aus einem Medium mit ε 1 > 0 auf Silber oder andere Metalle, sind im Frequenzbereich, in dem der Realteil der Permittivität Re (ε 2 ) < 0 wird, die Erhaltung von
kx = kx1 = kx2 und die Dispersionsrelationen
ω
ki 2 = ( ) 2εi = kx 2 + kzi 2
c
immer nur erfüllt, wenn es im zweiten Medium eine imaginäre Wellenvektorkomponente
in z-Richtung gibt. Ist die Dielektrizitätsfunktion negativ und reell, wird kz2 rein imaginär
und es entsteht ein rein evaneszentes Feld.
Für Einfallswinkel größer als θc kann ein evaneszentes Feld in das Metall eindringen,
dessen Tangentialkomponente groß genug ist, um mit der Tangentialkomponente der SPPMode an der Grenzfläche zwischen Metall und Luft (oder einem anderen Dielektrikum)
übereinzustimmen,
kx = kSPPx
ω
=
c
r
ε 3ε 2
.
ε3 + ε2
(3.9)
Wenn die Grenzfläche in Reichweite des evaneszenten Feldes liegt, kann das Feld mit
der SPP-Mode koppeln und es wird ein SPP angeregt. Der Vorgang wird als frustrierte
Totalreflexion oder optisches Tunneln bezeichnet11 . Die so erreichte Anregung sieht man
als Minimum der reflektierten Intensität.
Die SPP-Mode an der Grenzfläche zwischen Prisma und Metall kann in dieser Geometrie
- 31 -
nicht angeregt werden, da der Wellenvektor dieses SPPs immer größer ist als der des aus
dem Prisma einfallenden Lichts. Um ein SPP an dieser Grenzfläche anregen zu können,
benötigt man zwischen Prisma und Metallschicht eine zusätzliche dielektrische Schicht,
deren Brechungsindex kleiner ist als der des Prismas. Werden beide Moden angeregt,
kann für einen dünnen Metallfilm die Wechselwirkung der beiden Moden nicht ignoriert
werden. Ist der Film jedoch dick genug, kann jede der beiden Moden einer Oberfläche
zugeordnet werden51 .
3.1.2 Otto-Konfiguration
ϴi
ε1 Glas
ε2 Luft
ε3 Silber
Abbildung 2: Schematische Darstellung der Otto-Konfiguration.
Ist der Metallfilm zu dick für die Reichweite des evaneszenten Feldes, kann die OttoKonfiguration verwendet werden. Bei der Otto-Konfiguration ist zwischen dem Prisma
und dem Metallfilm ein dünner Luftspalt. Es wird mit der durch das Prisma vergrößerten
Tangentialkomponente des einfallenden Lichts an der zum Prisma zeigenden Seite - der
Grenzfläche zwischen Luft und Metall - ein SPP angeregt. Der Luftspalt ist allerdings
experimentell schwer zu kontrollieren, da er kleiner als die Wellenlänge von sichtbarem
Licht sein muss.
3.2 SPPs an einer Silber/Luft Grenzfläche
Um das Kopplungsverhalten von SPPs genauer zu analysieren, werden in dieser Arbeit
zwei Kretschmann-Konfigurationen behandelt. Mit der Transfermatrixmethode (siehe
Anhang A.2) wurden in Matlab die reflektierte Intensität, die elektromagnetischen Felder und der Poyntingvektor für die Schichtsysteme berechnet. Für die erste behandelte
Kretschmann-Konfiguration wurde eine semiunendliche Glasschicht, ein 55 nm dicker
Silberfilm und eine semiunendliche Luftschicht angenommen. Zur Berechnung der dielektrischen Funktion von Silber wurde ein durch die dielektrische Konstante ε ∞ modifiziertes
Drude-Modell verwendet,
- 32 -
ε = ε∞ −
ωp
.
ω (ω + iγ )
(3.10)
Der Polarisationshintergrund geht mit ε ∞ = 3.7 ein. Die natürliche Resonanzfrequenz
von Silber wird mit ωp = 9.17eV angenommen, die Dämpfung im Silber mit γ = 0.018eV .
Imaginärteil
Realteil
50
7
Drudemodell
Johnson & Christy
6
0
5
−50
Im(ε)
Re(ε)
4
−100
3
−150
2
−200
1
Drudemodell
Johnson & Christy
−250
0
0
1
2
3
4
5
6
7
0
1
2
ω [eV]
3
4
5
6
ω [eV]
Abbildung 3: Dielektrische Funktion von Silber: Experimentelle Werte aus Messungen an Silberfilmen
von Johnson und Christy18 im Vergleich zur dielektrischen Funktion des modifizierten
Drude-Modells.
Die große Abweichung des Imaginärteils der dielektrischen Funktion zwischen den
experimentellen Werten und dem in den folgenden Rechnungen verwendeten modifizierten Drude-Modell, die in Abb. 3 bei höheren Frequenzen zu sehen ist, rührt daher,
dass in diesem Modell die Interbandübergänge im UV-Bereich nicht beachtet werden
(vergleiche 1.5.1). Die Interbandübergänge im UV-Bereich führen zu verstärkter Absorption, die bei circa 4.5 eV ein Maximum erreicht. Im Bereich des sichtbaren Lichts ist die
Übereinstimmung des Modells mit den experimentellen Werten jedoch relativ gut.
Die obere Grenzfrequenz zur Anregung von SPPs an der Silber/Luft Grenzfläche erhält
man aus dem Maximum der Dispersionsrelation,
kSPPx
ω
=
c
r
ε
.
1+ε
Unter Vernachlässigung der Dämpfung ergibt sich ωsp = 4.23eV .
- 33 -
(3.11)
7
5
4.5
4
3.5
ω [eV]
3
2.5
2
1.5
ω sp LS
k LLG la s
k LLLuft
1
0.5
k SP P LS
0
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
k x [nm −1 ]
Abbildung 4: Gezeigt ist die Dispersionrelation der SPPs an einer Silber/Luft Grenzfläche. Die Dispersionskurve hat einen Schnittpunkt mit der Lichtlinie des Glases. Daraus folgt: Mit der
Kretschmann-Konfiguration können SPPs, deren Dispersion zwischen der Lichtlinie
der Luft und der Lichtlinie des Glases liegt, angeregt werden.
Für niedrige Frequenzen ω → 0 werden die SPPs photonartig und nähern sich der
Lichtlinie asymptotisch. Für εAд → (−∞+0.0i) geht die Eindringtiefe (siehe 3.15) der SPPs
im dielektrischen Medium gegen unendlich, während sie im Metall gegen Null geht. Die
Propagationslänge (siehe 3.13) der SPPs geht gegen unendlich. Für hohe Frequenzen wird
die Dispersionskurve flach. Die SPPs propagieren nicht mehr, sie werden zu longitudinalen
Oszillationen, SPs.29 .
Für die Dispersionsrelation eines Schichtsystems gibt es keine explizite analytische
Lösung. Der Resonanzwinkel kann mit dem Wellenvektor kSPPx für eine Grenzfläche
genähert werden:
εm εd
ω√
=
εд sin θ .
εm + εd
c
q
d
) 9,15 .
Der Resonanzwinkel ist dann genähert θ = arcsin( εд (εεmmε+ε
d)
kSPPx
ω
=
c
r
- 34 -
(3.12)
3.2.1 Reflektivität
Die Reflektivität des 55 nm dicken Silberfilms in der Kretschmann-Konfiguration wurde
mit der Transfermatrixmethode berechnet (siehe Anhang A.2). Die Anregung von SPPs
wird in den winkelabhängigen Reflexionsspektren als Minimum der Intensität sichtbar
(siehe Abb. 5b). Das im Bereich des Resonanzwinkels eingestrahlte Licht regt SPPs an und
wird im Weiteren vom Metall absorbiert. Für Wellenlängen kleiner als etwa 500 nm ändert
sich der Resonanzwinkel stark mit der Wellenlänge. Dies entspricht dem Abbiegen der
Dispersionskurve von der Lichtgeraden bei höheren Frequenzen, wie in Abb. 4 zu sehen
ist. Stellt man die Reflektivität statt in Abhängigkeit von Wellenlänge und Einfallswinkel
in Abhängigkeit von Energie und Wellenzahl dar, dann sieht man, dass der Verlauf der
Reflexionsminima die Dispersionskurve aus Abb. 4 wiedergibt. Für Einfallswinkel, die
kleiner sind als der kritische Winkel der Totalreflexion, ist die Reflektivität hauptsächlich
durch den Silberfilm bestimmt. Diese ist im Bereich der Wellenlängen des sichtbaren Lichts
sehr hoch. Erst bei Wellenlängen kleiner als 250 nm beginnt die Ultraviolett-Transparenz.
a
1
b
200
1
0.9
0.9
0.8
0.8
400
0.7
0.6
0.6
0.5
500
0.5
600
0.4
0.4
0.3
Reflektivität
0.7
λ [nm]
Reflektivität @ λ = 350 [nm]
300
0.3
700
0.2
0.2
800
0.1
0.1
900
0
30
40
50
60
70
80
90
30
Θ[ ]
40
50
60
70
80
90
Θ [ ◦]
◦
Abbildung 5: a. Die Reflektivität ist als Funktion des Einfallswinkels Θ aufgetragen. Den Resonanzwinkel für die Anregung des SPPs mit Licht der Wellenlänge λ = 350 nm sieht man
als Minimum der reflektierten Intensität. Der kritische Winkel der Totalreflexion ist
durch die strichlierte Linie gekennzeichnet.
b. Plot der Reflektivität in Abhängigkeit vom Einfallswinkel und der Wellenlänge des
eingestrahlten Lichts. Man sieht die Dispersionsrelation der SPPs als Minimum der
Reflexion.
- 35 -
a
1
b
4.5
1
4
0.8
3.5
0.8
0.6
3
0.5
2.5
0.4
0.5
Reflektivität
0.7
0.6
0.7
E [eV]
Reflektivität @ E = 3.5 [eV]
0.9
0.9
0.3
2
0.2
0.4
1.5
0.1
0.3
1
0.005
0.01
0.015
0.02
k x [nm
−1
0.025
0.03
0.005
0.01
0.015
0.02
0.025
0.03
k x [nm −1 ]
]
Abbildung 6: a. Die Reflektivität des einfallenden Feldes ist als Funktion von k x aufgetragen. Die
Wellenzahl für die Anregung eines SPPs mit der Energie 3.5 eV ist als Minimum sichtbar.
b. Die Dispersionsrelation ist als Minimum der Reflexion sichtbar. SPPs, deren Dispersion zwischen der Lichtlinie der Luft und der Lichtlinie des Glases liegt, können angeregt
werden.
- 36 -
3.2.2 Elektromagnetisches Feld
2
1.8
80
1.6
1.4
70
60
1
Ez
Θ
1.2
0.8
50
0.6
0.4
40
0.2
30
0
50
100
150
200
z [nm]
0.6
80
0.5
70
60
0.3
50
Ex
Θ
0.4
0.2
40
0.1
30
0
50
100
150
200
z [nm]
450
400
80
350
70
300
Hy
Θ
250
60
200
50
150
100
40
50
30
0
50
100
150
200
z [nm]
Abbildung 7: Für die Kretschmann-Konfiguration, die mit aus der negativen z-Richtung kommendem,
TM-polarisiertem weißen Licht bestrahlt wird, sind die Feldkomponenten Ez , E x und
Hy in z-Richtung abgebildet. Die Grenzfläche zwischen Glas und Silberfilm liegt bei
z = 0 nm, die Grenzfläche zwischen Silberfilm und Luft liegt bei z = 55 nm.
- 37 -
Um das Spektrum von TM-polarisiertem weißen Licht zu simulieren, wurde über Felder
der Wellenlängen zwischen 300 und 800 nm summiert. In Abb. 7 sieht man, dass das
elektromagnetische Feld durch die Anregung der SPPs an der Grenzfläche zwischen Silber
und Luft im Verhältnis zum einfallenden Feld stark verstärkt wird. Das elektromagnetische Feld der SPPs ist an die Oberfläche gebunden und fällt normal zu ihr exponentiell ab.
Die Tangentialkomponenten Ex und Hy sind stetig an den Grenzflächen. Die Normalkomponente Ez ist unstetig an den Grenzflächen. In Abb. 7b ist bei 42◦ ein Kante zu sehen,
die dem kritischen Winkel der Totalreflexion zwischen Glas und Luft entspicht.
3.2.3 Propagationslänge
Da der Wellenvektor der SPPs auch in x-Richtung einen Imaginärteil hat, fällt die Am00
plitude entlang der Oberfläche exponentiell mit e (−kS P P x x ) ab. Die Propagationslänge ist
definiert als die Distanz, in der die Intensität der Welle um das e1 -fache abgenommen hat,
und ist gegeben mit
LSPPx =
1
00
.
(3.13)
2kSPPx
An einer Silber/Luft Grenzfläche mit der relativen Permittivität von Silber bei 600 nm,
εr (eV ) = −16.4 + i0.207, ergibt sich eine Propagationslänge von Lspp = 112.9 µm.
3.2.4 Eindringtiefe
Der Imaginärteil der komplexen dielektrischen Funktion von Metallen ist gegenüber
dem Realteil klein. Wird der Imaginärteil der dielektrischen Funktion vernachlässigt, so
wird der Wellenvektoranteil kzi , der normal auf die Grenzfläche steht, rein imaginär. Der
Transversalanteil der Oberflächenwelle hat dann keinen propagierenden Anteil mehr, er
ist rein evaneszent. Die Amplitude nimmt von der Grenzfläche in die Medien exponentiell
ab. Die Eindringtiefe Lzi ist definiert als die Distanz, in der die Amplitude normal zur
Grenzfläche um das e1 -fache abgenommen hat,
ω
kzi =
c
c
Lzi =
ω
s
s
εi2
εm + εd
(3.14)
0 | +ε
|εm
d
.
εi2
(3.15)
An einer Silber/Luft Grenzfläche mit der relativen Permittivität von Silber bei 600 nm,
εr (eV ) = −16.4+i0.207, ist die Eindringtiefe ins Silber Lzm = 24.6 nm und die Eindringtiefe
in die Luft Lzd = 396.6 nm29 .
- 38 -
@ λ = 6 00 [nm]
@ λ = 600 [nm]
0.06
0.04
80
0.035
0.05
0.03
70
◦
0.04
60
Ez
Θ
@ Θ = 43
0.025
0.03
0.02
0.015
50
0.02
40
0.01
0.01
0.005
30
0
50
100
150
200
250
0
50
100
150
z [nm]
z [nm]
@ λ = 6 0 0 [nm]
@ λ = 600 [nm]
200
250
−4
−3
x 10
x 10
14
3
80
12
2.5
70
8
60
1.5
Ex
2
Θ
@ Θ = 43
◦
10
6
50
4
1
40
2
0.5
30
0
50
100
150
200
250
0
50
100
150
z [nm]
z [nm]
@ λ = 6 00 [nm]
@ λ = 600 [nm]
200
250
11
10
80
7
9
6
8
6
60
Hy
7
5
Θ
@ Θ = 43
◦
70
5
4
4
50
3
3
2
40
1
2
30
0
50
100
150
200
250
0
z [nm]
50
100
150
200
250
z [nm]
Abbildung 8: Für die Kretschmann-Konfiguration, die mit aus der negativen z-Richtung kommendem, TM-polarisiertem Licht der Wellenlänge λ = 600 nm bestrahlt wird, sind die
Feldkomponenten Ez ,E x und Hy in z-Richtung abgebildet. a. An der Stelle des Winkels
der maximalen Resonanz Θ = 43◦ ist der exponentielle Abfall von der Silber/Luft
Grenzfläche bei 55 nm in die Medien zu sehen. b. Mit Licht der Wellenlänge λ = 600
nm können für Einfallswinkel um Θ = 43◦ SPPs angeregt werden.
- 39 -
3.3 Energietransport durch ein Schichtsystem
Die Energieflussdichte durch ein Medium beschreibt man über den zeitlich gemittelten
Poyntingvektor:
1
hSi = Re (E × H∗ ).
2
(3.16)
Der Poyntingvektor für TM-polarisiertes Licht hat die Komponenten:
1
hSz i = Re (Ex Hy∗ )
2
(3.17)
1
hSx i = Re (−Ez Hy∗ ).
2
(3.18)
Das zeitliche Mittel des Poyntingvektors normal zur Oberfläche, hSz i, beschreibt den
Energiefluss durch die Oberfläche.
Nicht absorbierende Medien
Fällt Licht durch ein Schichtsystem, dessen erste Schicht optisch dichter ist als die zweite,
n 1 > n 2 , wird, wie man in 3.1.1 sehen konnte, für Materialien mit reellen Permittivitäten
√
und einem Einfallswinkel des Lichts größer θ > arcsin( nn21 ) die Wellenzahl kx > ε 2 ( ωc ) 2 .
Damit die Impulserhaltung für kx und die Dispersionsrelation im zweiten Medium erfüllt
0
0
0
werden können, wird in diesem Fall die Wellenzahl in z-Richtung kz imaginär, kz → ikz .
Ins zweite Medium können keine propagierenden Wellen eindringen.
Die räumliche Abhängigkeit der elektromagnetischen Felder hat die Form
0
e ik2 r = e ikx x −kz2z .
Können sich nur evaneszente Felder in z-Richtung ausbreiten, wird die gesamte Energie
der einfallenden Welle an der Grenzfläche reflektiert. Es gibt keinen Netzenergietransport
ins zweite Medium. Exponentieller Abfall der Amplitude des elektrischen Feldes bedeutet
also nicht unbedingt Absorption von Feldenergie. Evaneszente Felder transportieren
keine Energie. Entlang der Oberfläche in x-Richtung wird zwar Energie transportiert;
da das beschriebene Schichtsystem in x-Richtung als unendlich ausgedehnt angenommen wird, ist hier aber nur die Veränderung des Poyntingvektorfeldes in z-Richtung
maßgeblich. Kein Nettoenergietransport normal zur Oberfläche heißt nicht, dass das
evaneszente Feld keine Energie enthält - die zeitlich gemittelten Werte können nur die
instantanen Energieflüsse, die lokalen Ströme und zeitabhängigen Ladungsverteilungen
nicht enthalten32,39 .
- 40 -
Absorbierende Medien
Um die Absorption zu modellieren, muss die dielektrische Funktion einen Imaginärteil
00
00
ε haben. Durch den Beitrag von ε ist der Wellenvektor in z-Richtung nicht mehr
0
00
rein imaginär, kz → ikz − kz . Dieser Teil der Welle beeinflusst zwar die Amplitude des
0
evaneszenten Feldes nicht, der Abfall der Amplitude von Sz kommt von k , verursacht
00
aber eine Phasenveränderung in z-Richtung und so wird für ε , 0 im zweiten Medium
Sz , 0:
Hy e ik2 r−ωt = Hy e ikx x −kz z−ikz z−iωt .
0
00
Der Abfall des Energieflusses mit der Distanz − dS
dz ist proportional zur ins Medium
dissipierten Energie34 .
Dort, wo ein SPP entsteht, gibt es zwei Dissipationsmechanismen: Die soeben beschrie00
bene interne Dämpfung, die über das frequenzabhängige ε passiert. Diese Energie der
SPPs wird in Wärme umgewandelt. Ein zweiter Dissipationsmechanismus ist die Strahlungsdämpfung. Wenn aus dem Glas Strahlung in die SPP Mode gekoppelt wird, kann
Strahlung auch zurückgekoppelt werden. Die Richtung, in die das Licht emittiert wird,
√
ist gegeben durch kSPP = ε 0 ωc sinθr für eine glatte Grenzfläche in die gleiche Richtung
wie der reflektierte Strahl. Auch diesen Prozess nennt man optisches Tunneln29,39 .
In einem Dreischichtsystem, einer Kretschmann-Konfiguration mit n 2 < n 3 < n 1 , gibt
es drei verschiedene Bereiche für den Einfallswinkel, in denen sich die Felder und die
transmittierten Intensitäten unterschiedlich verhalten.
1. Für θi < arcsin( nn21 ) oder kx < ωc n 2 ist das Feld durchgehend propagierend und die
Intensität wird ins Fernfeld übertragen.
2. Für arcsin( nn21 ) < θi < arcsin( nn13 ) oder ωc n 2 < kx < ωc n 3 ist das Feld im Medium 2
evaneszent und im Medium 3 wieder propagierend. Die Intensität nimmt um so
stärker ab, je dicker die zweite Schicht ist. Das wird als frustrierte Totalreflexion
oder optisches Tunneln bezeichnet.
3. Für θi > arcsin( nn31 ) oder kx > ωc n 3 im Medium 2 und 3 ist das Feld evaneszent. Es
wird keine Intensität ins Medium 3 transmittiert.32
Im Schichtsystem gilt also, dass die Impulserhaltung die Energietransmission durch die
Schichten verhindert, wenn der Einfallswinkel über dem kritischen Winkel θi > arcsin( nn31 )
liegt.
- 41 -
40
35
80
30
70
60
20
Sz
Θ
25
15
50
10
40
5
30
0
0
50
100
150
200
z [nm]
Abbildung 9: Für die Kretschmann-Konfiguration, die mit aus der negativen z-Richtung kommendem,
TM-polarisiertem weißen Licht bestrahlt wird, ist der zeitlich gemittelte Poyntingvektor
in z-Richtung abgebildet. Die Grenzfläche zwischen Glas und Silberfilm liegt bei z = 0
nm, die Grenzfläche zwischen Silberfilm und Luft liegt bei z = 55 nm.
Man sieht: Auch für absorbierende Materialien gilt für Einfallswinkel über dem kritischen
Winkel θi > arcsin( nn13 ), dass die Impulserhaltung die Energietransmission über die zweite
Grenzfläche verhindert.
−5
−4
x 10
@ λ = 6 0 0 [nm], li = 3 9 4 [nm]
x 10
@ λ = 600 [nm], li = 394 [nm]
8
9
80
8
7
7
6
6
60
5
Ez
5
Θ
Sz @ Θ = 43
◦
70
4
4
3
50
3
2
2
40
1
1
30
0
0
50
100
150
200
250
0
0
z [nm]
50
100
150
200
250
z [nm]
Abbildung 10: Der zeitlich gemittelte Poyntingvektor in z-Richtung in der KretschmannKonfiguration für TM-polarisiertes Licht mit einer Wellenlänge von 600 nm. a. Man
sieht den Abfall der z-Komponente des Poyntingvektors an der Stelle des Winkels der
maximalen Resonanz Θ = 43◦
- 42 -
Kapitel
4
SPP-verstärkte Licht-Molekül-Wechselwirkung
4.1 Molekulare Anregungen fluoreszenter Moleküle
Als molekulare Anregung - Molecular Excitation (ME) - wird ein Quantenzustand eines Moleküls bezeichnet, der nicht der Grundzustand ist. Fluorophore sind Moleküle,
bei denen durch die Wechselwirkung mit Licht elektronische Übergänge möglich sind,
die zur Fluoreszenz führen. Organische fluoreszente Farbstoffe gehören zu den Fluorophoren. Moleküle können sich in verschiedenen Energieniveaus im Grundzustand
befinden, abhängig von der spezifischen Anordnung ihrer molekularen Orbitale. Der
niedrigste elektronische Übergang eines organischen Moleküls findet zwischen dem
höchsten besetzten molekularen Orbital - Highest Occupied Molecular Orbital (HOMO) und dem niedrigsten unbesetzten molekularen Orbital - Lowest Unoccupied Molecular
Orbital (LUMO) - statt. Der Grundzustand der meisten organischen Moleküle ist ein
elektronischer Singlett-Zustand S 0 , der erste angeregte Zustand S 1 ebenfalls. Zusätzlich
zu den elektronischen Energieniveaus haben größere Moleküle Vibrationsfreiheitsgrade,
daher hat jedes elektronische Energieniveau eine Vielzahl von Vibrationsenergieniveaus.
Bei Raumtemperatur befinden sich die Moleküle meist im niedrigsten Vibrationsniveau
des Grundzustandes, weshalb die Anregung normalerweise von diesem Energieniveau
beginnt. Resonante Absorption von Licht findet statt, wenn die Energie genau mit dem
elektronischen Übergang des Moleküls übereinstimmt; das Molekül wird in einen Vibrationsgrundzustand des LUMO angeregt. Ist mehr Energie vorhanden, wird das Molekül in höhere Vibrationszustände des LUMO angeregt, von wo es unter Energieverlust
nicht radiativ in den Grundzustand des LUMO relaxiert (Vibrationsrelaxation). Aus dem
Grundzustand des LUMO relaxiert das Molekül dann in einen Zustand des HOMO; diese
radiative Relaxation ist die Fluoreszenz. Für ein fluorszentes Molekül ist die Lebenszeit
des angeregten Zustandes typischerweise im Bereich von wenigen Nanosekunden bis zu
einigen Mikrosekunden. Im HOMO geht das Molekül dann durch Vibrationsrelaxation in
den niedrigsten Vibrationszustand des Grundzustandes über. Die Wellenlängen des Emissionsspektrums sind durch die Vibrationsrelaxation gegenüber den Wellenlängen des
Absorptionsspektrums rot verschoben; das wird als Stokes-Verschiebung bezeichnet.32,35
4.2 Kopplung zwischen MEs und SPPs
Im Bereich des optischen Spektrums können SPPs durch MEs fluoreszenter Farbstoffmoleküle angeregt werden und vice versa. Mit einer Kretschmann-Geometrie können
Farbstoffmoleküle in der Nähe der Silberoberfläche durch SPPs angeregt werden und mit
diesen koppeln. Die Energie der SPPs ist von der Projektion des Wellenvektors in die
Silberebene abhängig, dieser hängt vom Einfallswinkel des Lichts ab. Die Energie von
SPPs kann also über den Einfallswinkel so gewählt werden, dass sie mit der Energie der
MEs resonant werden. In diesem Fall können Moleküle angeregt werden und mit den
SPPs koppeln. Diese Kopplung zwischen MEs und SPPs führt zu neuen polaritonischen
Zuständen, SPP-ME-Hybrid-Moden.
m1
m2
κ1
κ12
κ2
x1
x2
Abbildung 1: Gekoppelte Oszillatoren
Die Kopplung zwischen einer ME und einem SPP kann mit einem Modellsystem zweier
gekoppelter, klassischer, harmonischer Oszillatoren genähert werden. Aus den Bewegungsgleichungen zweier gekoppelter, ungedämpfter Oszillatoren,
m 1ẍ 1 + (κ 1 + κ 12 )x 1 − κ 12x 2 = 0
(4.1)
m 2ẍ 2 + (κ 2 + κ 12 )x 2 − κ 12x 1 = 0,
(4.2)
erhält man mit
xi = Xi e −iαt
ω12 =
κ 1 + κ 12
m
ω22 =
- 44 -
κ 2 + κ 12
m
κ 12
C2 = √
,
m 1m 2
(4.3)
wobei ωi die Kreisfrequenzen der Oszillatoren sind und C der Stärke der Kopplung
zwischen den Oszillatoren entspricht, mit

− κm121
ω12 + α 2

X1



0

 =  ,
− κm122 ω 22 + α 2   X 2   0 

(4.4)
folgendes charakteristisches Polynom:
α 4 − (ω 12 + ω22 )α 2 + ω 12ω22 − C 4 = 0.
(4.5)
Daraus ergeben sich α ±2 , die Eigenwerte des gekoppelten Systems:
α ±2
=
(ω12 + ω22 ) ±
q
(ω12 − ω22 ) 2 + 4C 4
.
(4.6)
2
Im Resonanzfall für ω1 = ω 2 = ω 0 sind die neuen Moden die Normal- oder Hybridmoden
des gekoppelten Systems31 :
α −2 = ω 02 − C 2 .
α +2 = ω02 + C 2
Für m 1 = m 1 = m ist
α+ =
k + 2κ
m
α− =
k
.
m
(4.7)
(4.8)
Man sieht, der Frequenzabstand der zwei Moden hängt von der Kopplung C ab, je stärker
die Kopplung, umso größer die Aufspaltung. Ist das System gedämpft, kommen für die
Dämpfung noch γ 1ẋ 1 und γ 2ẋ 2 hinzu. Die Kopplung ist umso effizienter, je kleiner die
Verstimmung ω1 − ω 2 der Oszillatoren ist und je kleiner die Linienbreiten γi sind44 .
4.3 Starke Kopplung
Die Wechselwirkung zwischen SPPs und MEs kann als stark oder schwach charakterisiert
werden. Ist die Kopplung schwach, gilt Fermis Goldene Regel, die Wechselwirkung kann
störungstheoretisch behandelt werden. Im Oszillatormodell kann, solange die Kopplung
schwach ist, einer der Oszillatoren als Donor und der andere als Akzeptor betrachtet
werden, die Energie geht vom Donor zum Akzeptor. Ist die Stärke der Wechselwirkung
jedoch groß genug, wird der Energierücktransfer möglich. Es wird unmöglich, zwischen
Donor und Akzeptor zu unterscheiden. Das System ist im Bereich der starken Kopplung.
Wenn das System lange genug kohärent bleibt, können Rabioszillationen stattfinden31 .
Der Energieaustausch findet dann mit einer Periode invers zur Rabifrequenz statt. Wie
man in 4.7 sehen konnte, hat das gekoppelte System neue, gegenüber den ungekoppelten
Eigenzuständen verschobene Eigenzustände14 . D.h. die Energieniveaus der Moleküle, die
für die Absorption verantwortlich sind, unterscheiden sich von denen des ungekoppelten
- 45 -
Systems. Wie stark das Energiespektrum des Hybridsystems modifiziert ist, hängt von der
Stärke C der Kopplung ab. Ein wichtiges Charakteristikum der starken Kopplung ist das
Rabisplitting. Die Dispersionskurve zweier stark gekoppelter Oszillatoren hat zwei Äste,
die sich nicht schneiden. Das wird auch als Anticrossing bezeichnet. Das Rabisplitting
oder Normalmodesplitting entspricht dem minimalen Energieabstand der zwei Äste ∆E.
Der Abstand der zwei Moden ist proportional zur Stärke der Kopplung, das Splitting
nimmt mit der Stärke der Kopplung zu. Der Bereich der starken Kopplung zwischen Licht
und Materie wird oft als der Bereich definiert, in dem die Kopplung so groß ist, dass
im Verhältnis zu den Linienbreiten das Rabisplitting experimentell sichtbar wird44 . Die
Stärke der Wechslwirkung zwischen ME und SPP kann im Bereich der starken Kopplung
über das Rabisplitting approximiert werden7 . Wenn das System schwach gekoppelt ist,
ist das nicht möglich, da sich die Äste der Dispersionskurve schneiden.
4.4 SPP-Molekül-Wechselwirkung
Eine Möglichkeit, die Kopplung zwischen Licht und Materie weiter zu verstärken, ist das
Dipolmoment des Molekülanteils zu verstärken. Dafür eignen sich Materialien mit großer
Oszillatorstärke in hoher Konzentration. Fluorophore und organische Halbleiter sind
wegen ihrer großen Oszillatorstärke bei Raumtemperatur gute Kanditaten, um mit dem
durch SPPs stark amplitudenverstärkten und stark lokalisierten elektromagnetischen Feld
des Lichts im sichtbaren und nahen infraroten Bereich starke Kopplung zu erreichen42 .
Klassisch gibt es keine Erklärung dafür, warum manche Absorbtions-/Emissionslinien
stärker sind als andere. Man weist jeder Resonanzfrequenz ω0i eine phänomenologische
P
Oszillatorstärke fi zu, die Oszillatorstärken werden so normiert, dass fi = 1 ist10 .
Da die Licht-Molekül-Wechselwirkung resonanten Charakter hat, kann man sie als
quantenmechanisches Zwei-Niveau-System nähern, man betrachtet dafür nur die zwei
Niveaus, deren Energiedifferenz in der Nähe der Wechselwirkungsenergie ~ω 0 liegt32 .
Quantenmechanisch sieht man mit Fermis Goldener Regel, dass die verschieden starken
Übergänge aus der Übergangswahrscheinlichkeit kommen. Die Matrixelemente der
Übergänge heißen auch elektrische Dipolmatrixelemente, M 12 = h2|exE|1i, 1 steht
hier für den Anfangszustand, 2 für den Endzustand und ex ist der Dipoloperator. Der
Wechselwirkungs-Hamilton entspricht dem Dipolmoment eines Elektrons im elektrischen Feld, H 0 = −pE. Die Übergänge nennt man elektrische Dipolübergänge, sie sind
direkt proportional zu den Oszillatorstärken10 . Durch eine hohe Molekülkonzentration
wird die Anzahl der möglichen Dipolübergänge erhöht, was zu verstärkter Absorption
führt.
- 46 -
4.4.1 Kopplung von SPPs mit Sulforhodamin 101
Im Folgenden wird die Kopplung zwischen SPPs und Sulforhodamin 101 untersucht. Um
die Anregung von Sulforhodamin 101 Molekülen durch SPPs und die Kopplung zwischen
diesen MEs und SPPs zu SPP-ME-Hybridmoden zu untersuchen, wird eine KretschmannKonfiguration angenommen, die mit TM-polarisiertem weißen Licht bestrahlt wird.
Die Kretschmann-Konfiguration besteht aus einem Glasprisma, einem 55 Nanometer
dicken Silberfilm, einer 50 Nanometer dicken Schicht aus einem Dielektrikum, in dem
Sulforhodamin 101 Moleküle homogen verteilt sind, und einer Luftschicht.
ϴi
ε1 Glas
ε2 Silber
ε3 Sulforhodamin 101
ε4 Luft
Abbildung 2: Schematische Darstellung der Kretschmann-Konfiguration
Rhodamine sind Fluorophore. Sie gehören zur Gruppe fluoreszierender organischer
Farbstoffe und sind Derivate von Xanthenen, sie zählen zu den Xanthenfarbstoffen30 . Sie
sind wegen ihrer relativ scharfen Absorptionslinien im sichtbaren Bereich gut geeignet,
um mit SPPs stark zu koppeln.
Um das Kopplungsverhalten bei steigender Molekülkonzentration zu untersuchen,
wurden in einem Experiment an sechs Setups der oben beschriebenen KretschmannKonfiguration die reflektierte Intensität und die Lumineszenz gemessen. In dieser Arbeit
werden diese sechs Szenarien theoretisch behandelt. In den sechs Beispielen ist in
der dielektrischen Matrix Sulforhodamin in steigender Konzentration enthalten. Die
dielektrische Matrix enthält zwischen 0.3 und 4 mg Sulforhodamin 101. Die veränderte
Molekülkonzentration der Schicht geht über die Permittivität (siehe A.1) und die Energieniveaus der MEs in die Rechnungen ein. Die in den Rechnungen verwendeten Werte
(siehe Anhang A.1 Tabelle 3) stammen aus Absorptionsmessungen aus Ref.[2]. In diesen
Messungen wurde für sechs Samples, bestehend aus einer dielektrischen Matrix (aus
SU-8, einem Epoxidharz) mit unterschiedlichen Sulforhodamin 101 Molekülkonzentrationen, die Maxima der absorbierten Intensität bestimmt. Das Absorptionsspektrum
wurde mit zwei Lorentzkurven gefittet. Für die sechs Samples bleibt, bei steigender
Farbstoffkonzentration, die spektrale Position der Maxima der Absorption ungefähr
- 47 -
gleich.
Absorptionsspektrum von Sulforhodamin 101
Sample 1
Sample 2
Sample 3
2
Sample 4
Sample 5
Absorption [a.u.]
Sample 6
1.5
1
0.5
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
ω [eV]
Abbildung 3: Absorptionsspektren der Sulforhodamin 101 Samples: Die gezeigten Absorptionsspektren wurden aus den Imaginärteilen der Permittivitäten (siehe Anhang A.1) der sechs
Samples berechnet.
In Abb. 3 sieht man, dass Sulforhodamin 101 im Bereich des sichtbaren Spektrums zwei
Absorptionsmaxima hat, bei circa 555 nm (2.07 eV) und bei circa 599 nm (2.23 eV). Die
Absorptionsmaxima können mit zwei MEs der Übergangsenergie EME1 und EME2 und
den Linienbreiten γME1 ≈ 0.15 und γME2 ≈ 0.14 angenähert werden2 . Die Linienbreiten
der MEs entsprechen den Halbwertsbreiten der Lorentzkurven.
Modellrechnungen zur Kopplung von SPPs mit Sulforhodamin 101
Mit der Transfermatrixmethode (siehe Anhang A.1) wurden mit Hilfe von Matlab die
Reflektivität des Schichtsystems und die elektromagnetischen Felder im Schichtsystem berechnet. Die Dispersion der Energieeigenwerte der SPP-ME-Hybridmoden wurde mit dem
Oszillatormodell berechnet. Für die Rechnungen wurde eine semiunendliche Glasschicht,
eine 55 nm Silberschicht, eine 50 nm SU-8-Schicht mit verschiedenen Sulforhodamin 101
Konzentrationen sowie eine semiunendliche Luftschicht angenommen. Die Ergebnisse der
Rechnungen werden mit entsprechenden gemessenen Werten, aus Reflektionsmessungen
an der beschriebenen Kretschmann-Konfiguration, aus Ref.[2] verglichen.
- 48 -
4.4.2 Oszillatormodell
Quantenmechanisches Zwei-Niveau-System
Für ein SPP mit Energie ESPP und ein Farbstoffmolekül mit einem erlaubten (elektronischen) Absorptionsübergang bei einer Energie EME mit einer Linienbreite γME kann die
Eigenwertgleichung mit Hilfe des Wechselwirkungs-Hamilton-Operators in der Basis
|x 1 i, |x 2 i der ungekoppelten Eigenzustände für das Oszillatormodell wie folgt geschrieben
werden:


ESPP − iγSPP
C

x1


x1


 = En 
.
C EEx − iγEx   x 2 
x2 
(4.9)
ESPP ist die Energie des ungekoppelten SPPs an der Grenze zwischen Silber und der
dielektrischen Matrix, in der keine absorbierenden Moleküle enthalten sind, γSPP ist
die Linienbreite des ungekoppelten SPPs. Die Linienbreite wird vom Wellenvektor bzw.
Einfallswinkel unabhängig angenommen und wurde mit der Dämpfung der Elektronen
im Silber genähert. C ist die Kopplungstärke zwischen ME und SPP.
1
1q
En± = (ESPP − iγSPP + EME − iγME ) ±
((ESPP − iγEspp ) − (EME − iγME )) 2 + 4C 2 (4.10)
2
2
sind die Energieeigenwerte des gekoppelten Systems. Die Lösungen des Gleichungssystems beschreiben die zwei Äste der Dispersionskurve. Der Abstand zwischen oberem
und unterem Dispersionsast an der Stelle ESPP (θresonant ) = EME , der Resonanz, ist das
Rabisplitting,
∆E =
q
4C 2 − (γSPP − γME ) 2 .
(4.11)
Die zwei Dispersionsäste - oberer Polaritonast UPB und unterer Polaritonast LPB - entsprechen den zwei durch die Kopplung entstandenen, neuen Polariton-Moden.
Man sieht, die Differenz der Linienbreiten von ME und SPP muss entsprechend klein sein,
um starke Kopplung beobachten zu können7 .
Quantenmechanisches Drei-Niveau-System
Die Kopplung zwischen den zwei MEs, die den zwei Absorbtionsmaxima des Sulforhodamins 101 entsprechen, und dem SPP kann mit drei gekoppelten Oszillatoren genähert
werden. C 1 und C 2 (siehe Tabelle 1) sind die Parameter der Kopplungsstärken zwischen
den zwei MEs und dem SPP . ESPP ist die Energie des ungekoppelten SPPs, γSPP ist die Linienbreite des ungekoppelten SPPs. EME1 und EME2 sind die Energien der ungekoppelten
MEs, γME1 und γME2 sind die jeweiligen Linienbreiten (siehe Tabelle 1):
- 49 -

ESPP − iγSPP




C1
C2
C 1 EME1 − iγME1
C2


0 

0 EME2 − iγME2

x1


 x 2  = En




x3 


x1


 x2  .




x3 
(4.12)
Aus dem Oszillatormodell erhält man die Energieeigenwerte des gekoppelten Systems. In
den Dispersionsrelationen sieht man drei Dispersionsäste, die den drei Polariton-Moden
entsprechen. Es entsteht doppeltes Rabisplitting.
Rabisplitting
Wenn die Kopplung zwischen jedem der beiden MEs und dem SPP stark ist, entsteht
doppeltes Rabisplitting. In den Dispersionsrelationen der Energieeigenwerte in Abb. 4
sieht man drei Dispersionsäste, die den drei Polariton-Moden entsprechen. UPB ist der
obere Dispersionsast, MPB der mittlere Dispersionsast und LPB der untere Dispersionsast.
Man sieht doppeltes Rabisplitting.
Für die Samples 1 - 6 sieht man mit steigender Konzentration der Sulforhodamin 101
Moleküle die Verstärkung der Kopplung an der Zunahme des Rabisplittings. Das mit
der Transfermatrixmethode berechnete reflektierte Spektrum in Abb. 5 ist in guter
Übereinstimmung mit den Dispersionskurven der Energieeigenwerte in Abb. 4. Im
reflektierten Spektrum in Abb. 5 ist das doppelte Rabisplitting allerdings für Samples die
1 - 2 nicht zu sehen und für Samples die 3 - 6 nur schlecht.
An der Dispersion der reflektierten Intensität sieht man, dass die Dispersionskurve
gebogen wird, wenn die Frequenz der SPPs in die Nähe der Absorptionsfrequenz kommt,
d.h.
dω
dk ,
die Gruppengeschwindigkeit, nimmt ab44 . Die Propagation von SPPs wird durch
die Kopplung mit MEs geschwächt (vergleiche Kapitel 3 Abb. 5b).
- 50 -
Oszillatormodell - Energieeigenwerte
Sample 1
Sample 2
2.5
2.5
E [eV]
3
E [eV]
3
2
2
1.5
1.5
30
40
50
60
70
80
90
30
40
50
Θ [◦]
60
70
80
90
70
80
90
70
80
90
Θ [◦]
Sample 3
Sample 4
2.5
2.5
E [eV]
3
E [eV]
3
2
2
1.5
1.5
30
40
50
60
70
80
90
30
40
50
Θ [◦]
60
Θ [◦]
Sample 5
Sample 6
2.5
2.5
E [eV]
3
E [eV]
3
2
2
1.5
1.5
30
40
50
60
70
80
90
Θ [◦]
30
40
50
60
Θ [◦]
Abbildung 4: Mit dem Oszillatormodell für das Drei-Niveau-System berechnete Dispersion der Energieeigenwerte des gekoppelten Systems: Die Energieeigenwerte sind gegen den Einfallswinkel aufgetragen. Für die Samples 1 - 6 steigt die Molekülkonzentration.
- 51 -
Transfermatrixmethode - Reflektierte Intensität
Sample 1
Sample 2
3
1
3
0.9
0.8
0.7
2.5
E [eV]
E [eV]
0.6
0.5
0.4
2
Reflektivität
2.5
2
0.3
0.2
0.1
1.5
1.5
30
40
50
60
70
80
90
0
30
40
50
Θ [ ◦]
60
70
80
90
Θ [ ◦]
Sample 3
Sample 4
3
1
3
0.9
0.8
0.7
2.5
E [eV]
E [eV]
0.6
0.5
0.4
2
Reflektivität
2.5
2
0.3
0.2
0.1
1.5
1.5
30
40
50
60
70
80
90
0
30
40
50
Θ [ ◦]
60
70
80
90
Θ [ ◦]
Sample 5
Sample 6
3
1
3
0.9
0.8
0.7
2.5
E [eV]
E [eV]
0.6
0.5
0.4
2
Reflektivität
2.5
2
0.3
0.2
0.1
1.5
1.5
30
40
50
60
70
80
90
0
30
Θ [ ◦]
40
50
60
70
80
90
Θ [ ◦]
Abbildung 5: Mit der Transfermatrixmethode berechnetes Spektrum der reflektierten Intensität. Für
die Samples 1 - 6 steigt die Molekülkonzentration. Der MPB ist im Druck nicht sichtbar.
- 52 -
Reflektierte Intensität bei Einfallswinkel 63◦ .
Sample 2
Sample 1
0.9
0.9
Reflektivität @ Θ = 63 [ ◦ ]
Reflektivität @ Θ = 63 [ ◦ ]
0.8
0.7
0.6
0.5
0.4
0.3
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.2
0.1
0.1
1.5
2
2.5
3
1.5
2
E [eV]
E [eV]
Sample 3
Sample 4
0.95
2.5
3
2.5
3
2.5
3
0.95
Reflektivität @ Θ = 63 [ ◦ ]
Reflektivität @ Θ = 63 [ ◦ ]
0.9
0.85
0.8
0.75
0.7
0.65
0.6
0.9
0.85
0.8
0.75
0.7
0.65
0.55
0.6
1.5
2
2.5
3
1.5
2
E [eV]
E [eV]
Sample 5
Sample 6
0.95
0.9
Reflektivität @ Θ = 63 [ ◦ ]
Reflektivität @ Θ = 63 [ ◦ ]
0.9
0.85
0.8
0.75
0.7
0.65
0.8
0.7
0.6
0.5
0.6
0.4
0.55
0.5
0.3
1.5
2
2.5
3
1.5
2
E [eV]
E [eV]
Abbildung 6: Mit der Transfermatrixmethode berechnete reflektierte Intensität bei einem Einfallswinkel von Θ = 63◦ . Für Sample 3 - 6 sind die Maxima gut unterscheidbar, man sieht
doppeltes Rabisplitting.
- 53 -
Energieabstände der Rabisplittings
Sample 2, Θ1 = 53.4169, Θ2 = 58.8715
Sample 1, Θ1 = 51.7241, Θ2 = 56.0502
3
3
E [eV]
2.5
E [eV]
2.5
2
2
1.5
1.5
52
52.5
53
53.5
54
54.5
55
55.5
56
53.5
54
54.5
55
55.5
Sample 3, Θ1 = 64.9843, Θ2 = 77.3981
3
56
56.5
57
57.5
58
58.5
Θ [ ◦]
Θ [ ◦]
Sample 4, Θ1 = 63.1975, Θ2 = 75.1411
3
E [eV]
2.5
E [eV]
2.5
2
2
1.5
1.5
66
68
70
72
74
76
64
66
68
Θ [ ◦]
Sample 5, Θ1 = 66.7712, Θ2 = 81.442
3
70
72
74
Θ [ ◦]
Sample 6, Θ1 = 71.2853, Θ2 = 87.931
3
2.5
E [eV]
E [eV]
2.5
2
2
1.5
1.5
68
70
72
74
76
78
80
72
74
76
78
80
82
84
86
Θ [ ◦]
Θ [ ◦]
Abbildung 7: Zu sehen ist der Zoom auf die Minima der mit der Transfermatrixmethode berechneten
reflektierten Intensität. Das vollständige Spektrum ist in Abb. 5 abgebildet.
- 54 -
In Abb. 7 ist für alle sechs Samples doppeltes Rabisplittig sichtbar. Die Energieabstände
der Rabisplittings sind wie folgt definiert:
∆Elo = E 2 (θ 1 ) − E 1 (θ 1 )
(4.13)
∆Eup = E 3 (θ 2 ) − E 2 (θ 2 ).
(4.14)
∆Elo und ∆Eup sind die Werte des unteren und des oberen Energiesplits. E 1 (θ ) ist die
Energie des unteren Energieastes LPB, E 2 (θ ) ist die Energie des mittleren Energieastes
MPB und E 3 (θ ) ist die Energie des oberen Energieastes UPB. Um die Stelle des Energiesplittings zu finden, wurden die Schnittpunkte zwischen den Energien der ungekoppelten
MEs und der Dispersionsrelation des ungekoppelten SPPs ermittelt. Die Dispersionsrelation des ungekoppelten SPPs wurde für die Kretschmann-Konfiguration mit einer
SU-8 Schicht ohne Sulforhodamin 101 mit der Transfermatrixmethode berechnet. Die
Kopplungsstärken C 1 und C 2 wurden mit ∆E = 2C für zwei gekoppelte ungedämpfte
Oszillatoren genähert.
Tabelle 1 enthält die Energiesplits der mit dem Transfermatrixmodell berechneten
Reflektionsminima und die Energiesplits der Energieeigenwerte des Oszillatormodells,
sowie die Kopplungsstärken Cup und Clo und die Energien der ungekoppelten MEs, EME1
und EME2 . Um die Parameter für das Oszillatormodell zu erhalten, wurden die mit dem ∆E
aus der Transfermatrixmethode genäherten Werte der Kopplungsstärken Cup und Clo und
die mit der Transfermatrixmethode berechnete Dispersionrelation des ungekoppelten
SPPs verwendet.
Tabelle 1
Sample
EME1
EME2
∆Eup(T MM )
∆Elo(T MM )
∆Eup(osz)
∆Elo(osz)
Cup
Clo
1
2,08
2,26
0,076
0,203
0,038
0,05
0,038
0,102
2
2,07
2,25
0,089
0,229
0,05
0,1
0,045
0,115
3
2,06
2,25
0,178
0,318
0,18
0,229
0,089
0,159
4
2,05
2,24
0,229
0,356
0,2
0,25
0,115
0,178
5
2,05
2,22
0,254
0,381
0,23
0,28
0,127
0,191
6
2,05
2,23
0,275
0,345
0,25
0,36
0,178
0,229
- 55 -
Tabelle 2 enthält die Energiesplits der an der Kretschmann-Konfiguration gemessenen
reflektierten Intensität aus Ref. [2], die Kopplungsstärken Cup und Clo , die aus den Ener√
giesplits mit ∆E = 4C 2 genähert wurden, und die Energien der ungekoppelten MEs,
ME1 und ME2, sowie die Werte der Quadratwurzel des höheren und des niedrigeren
Absorptionsmaximums Aup und Alo .
Tabelle 22
Sample EME1 , eV
EME2 , eV
∆Eup , eV
∆Elo , eV
Cup , eV
Clo , eV
Alo , a.u. Aup , a.u.
3
2,07
2,25
0,09
0,20
0,045
0,105
2.93
1.19
4
2,07
2,25
0,12
0,22
0,058
0,12
3.52
1.56
5
2,06
2,23
0,16
0,26
0,082
0,12
4.24
1.92
6
2,06
2,25
0,19
0,33
0,120
0,15
4.97
2.10
a
0.5
b
0.28
0.26
0.45
0.24
0.4
Upper Split [eV]
Lower Split [eV]
0.22
0.35
0.3
0.2
0.18
0.16
0.14
0.25
0.12
0.2
Transfermatrixmethode
Oszillatormodell
gemessene Werte
Transfermatrixmodell
Oszillatormodell
gemessene Werte
0.1
0.08
2.5
3
3.5
4
(Absorption)
4.5
5
1
2
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
2.1
1
(Absorption) 2
Abbildung 8: Gezeigt sind die Breiten der Energiesplits als Funktion der Quadratwurzel der Absorption der mit dem Transfermatrixmodell berechneten Reflektionsminima, der mit dem
Oszillatormodell berechneten Energieeigenwerte und der gemessenen Reflektionsminima. a) Lower Split b) Upper Split
- 56 -
Beide Splits zeigen eine lineare Abhängigkeit. Sie steigen mit Zunahme der Molekülkonzentration. Die mit dem Transfermatrixmodell berechneten Werte für den Lower Split
liegen zwischen 318 und 345 meV, die Werte für den Upper Split liegen zwischen 178 und
275 meV. Die mit dem Oszillatormodell berechneten Werte für den Lower Split liegen
zwischen 229 und 360 meV, die Werte für den Upper Split liegen zwischen 100 und 250
meV. Die gemessenen Werte für den Lower Split liegen zwischen 200 und 330 meV, die
Werte für den Upper Split liegen zwischen 90 und 190 meV. Für die berechneten Werte
ist für alle sechs Fälle doppeltes Rabisplitting zu sehen (vergleiche Abb.7), beide MEs
koppeln stark mit den SPPs.
Konzentration
Aus der Dispersionsrelation für zwei unendliche Halbräume aus Silber und Rhodamin
kann mit Hilfe der Permittivitäten eine Gleichung genähert werden, deren zwei Lösungen den Normalmoden entsprechen. Man kann zeigen,
dass das Rabisplitting folgende
q
Abhängigkeit von der Molekülkonzentration hat:
N √e
V ε 0me .
Werden die MEs durch ein
quantenmechanisches Zwei-Niveau-System beschrieben und das SPP durch ein elekq
tromagnetisches Feld, kann man zeigen, dass das Rabisplitting proportional zu M 12 VN
ist44 .
- 57 -
Elektromagnetisches Feld
1
0.9
80
0.8
0.7
70
0.5
Ez
Θ
0.6
60
0.4
50
0.3
0.2
40
0.1
30
0
50
100
150
200
z [nm]
0.6
80
0.5
70
60
0.3
50
Ex
Θ
0.4
0.2
40
0.1
30
0
50
100
150
200
z [nm]
450
400
80
350
70
300
Hy
Θ
250
60
200
50
150
100
40
50
30
0
50
100
150
200
z [nm]
Abbildung 9: Für die Kretschmann-Konfiguration, die mit aus der negativen z-Richtung kommendem,
TM-polarisiertem weißen Licht bestrahlt wird, sind die Feldkomponenten Ez ,E x und
Hy in z-Richtung abgebildet. Die Grenzfläche zwischen Glas und Silberfilm liegt bei
z = 0 nm, die Grenzfläche zwischen Silberfilm und Molekülfilm liegt bei z = 55nm und
die Grenzfläche zwischen Molekülfilm und Luft liegt bei z = 105 nm.
- 58 -
Elektromagnetisches Feld im Schichtsystem
In Abb. 9 ist der exponentielle Abfall des elektromagnetischen Feldes in die Silberschicht zu sehen, man erkennt eine maximale Verstärkung des Feldes durch die SPP-MEHybridmoden bei Einfallswinkeln von circa 50◦ . Das elektromagnetische Feld, das in einer
Kretschmann-Konfiguration ohne Molekülschicht durch die Anregung mit weißem Licht
entsteht, wird durch die Anregung von SPPs bei Einfallswinkeln von circa 43◦ maximal
verstärkt und die Feldverstärkung ist höher - vergleiche Kapitel 3 Abb. 7. Die Verschiebung ist von der Dicke der SU-8-Sulforhodaminschicht und der Molekülkonzentration
in der Schicht abhängig. Bei 42◦ ist eine Kante zu sehen, die dem kritischen Winkel der
Totalreflexion zwischen Glas und Luft entspricht.
4.5 Energietransport durch das Schichtsystem
30
80
25
20
60
15
50
10
40
5
30
Sz
Θ
70
0
0
50
100
150
200
z [nm]
Abbildung 10: Zeitlich gemittelter Poyntingvektor in z-Richtung: Die Grenzfläche zwischen Glas und
Silberfilm liegt bei z = 0 nm, die Grenzfläche zwischen Silberfilm und Molekülfilm
liegt bei z = 55 nm und die Grenzfläche zwischen Molekülfilm und Luft liegt bei z =
105 nm.
Polariton-Moden, die durch SPP-ME-Kopplung in der Kretschmann-Konfiguration
entstehen, sind TM-polarisiert und an ideal glatten Oberflächen nicht radiativ, da der
Wellenvektor der Polaritonen immer größer ist als der Wellenvektor des Lichts in der
Luft42 . Es gilt die Impulserhaltung. An rauen Oberflächen erfolgt jedoch Streuung und es
kommt zur Abstrahlung von Licht.
- 59 -
Da in der idealisierten Kretschmann-Konfiguration keine Intensität durch die Luftseite
propagieren kann, wird die Energie, die in den Sulforhodamin 101 Film transportiert
wird, von den Molekülen absorbiert. Der Energiefluss, durch die Grenzfläche zwischen
Silberfilm und Molekülfilm, ist durch die z-Komponente des zeitlich gemittelten Poyntingvektors hSz i gegeben.
0.8
0.7
Intensität [a.u.]
0.6
0.5
0.4
0.3
0.2
0.1
30
40
50
60
70
80
Θ [ ◦]
Abbildung 11: z-Komponente des zeitlich gemittelten Poyntingvektors an der Grenzfläche zwischen
Silber und Sulforhodamin 101 Film, bei z = 55 nm, als Funktion des Einfallswinkels. Sie beschreibt den Energiefluss in den Molekülfilm und ist proportional zur
Fluoreszenzintensität.
Die Wahrscheinlichkeit der Anregung von SPP-ME-Polaritonen ist proportional zur
Energieflussdichte/Intensität. Die inhomogene Linienverbreiterung, die bei Ansammlung
organischer Moleküle neben der homogenen Linienverbreiterung immer entsteht, wird
durch Vibrationsmoden der Moleküle verursacht. Durch die inhomogene Linienverbreiterung entstehen neben den Polaritonen auch ungekoppelte MEs.
Um die Anregung und Relaxation der SPP-ME-Polaritonen weiter zu untersuchen, eignet
sich die Molekülfluoreszenz, da sie direkt mit der Besetzung der angeregten Zustände
zusammenhängt. Das an der ebenen Seite des Prismas abgestrahlte Licht setzt sich
zusammen aus der Lumineszenz, die durch Streuung der SPP-ME-Hybridmoden und SPPs
an der realen Struktur entsteht, und aus der Fluoreszenz der MEs. Die Lumineszenz ist
TM-polarisiert, während die Fluoreszenz großteils unpolarisiert ist, da die Moleküle in der
dielektrischen Matrix zufällig orientiert sind. Um die Fluoreszenz von der Lumineszenz
zu trennen, kann das transmittierte Signal TE-polarisiert werden19 .
- 60 -
In der Kretschmann-Konfiguration können mit TM-polarisiertem weißen Licht alle
Polariton-Moden angeregt werden, die zwischen den winkelabhängigen Lichtlinien des
Glases und der Luft liegen. Um die winkelabhängige Stärke/Wahrscheinlichkeit der Anregung und den daraus folgenden Energietransfer im Schichtsystem zu untersuchen,
wird die Fluoreszenz mit Hilfe des Drei-Niveau-Systems aus 4.12 berechnet. Aus der
Diagonalisierung des Hamilton-Operators des Drei-Niveau-Systems erhält man die Polaritoneigenzustände:
|ψn i = αn |x 1 i + βn |x 2 i + γn |x 3 i.
(4.15)
Die Koeffizienten α, β und γ sind vom Einfallswinkel und der Energie abhängig. n steht
für die drei Eigenzustände UPB, MPB und LPB.
Es wird angenommen, dass die Stärke der Anregung proportional zur Plasmonischen
Komponente, d.h. zum SPP ist, die mit dem Koeffizienten α gegeben ist. Die Wahrscheinlichkeit der molekularen Anregung ist durch β 2 + γ 2 gegeben. Die Wahrscheinlichkeit,
dass bei einem Winkel θ eine Polariton-Mode angeregt wird sowie des darauf folgenden
Zerfalls der Polaritonen durch Vibrationsrelaxation und Fluoreszenz der MEs ist proportional zum Produkt α 2 (β 2 + γ 2 ). Die volle Anregungs-/Fluoreszenz-Wahrscheinlichkeit
erhält man, indem man über alle drei Polaritonäste summiert. Sie ist proportional zu19
X3
α 2 [β 2
n=1 n n
+ γn2 ].
(4.16)
In Ref.[19] konnte an der Intensität der Fluoreszenz für eine äquivalente KretschmannKonfiguration, deren dielektrische Matrix allerdings Nilered Moleküle statt Sulforhodamin
101 Moleküle enthielt, gezeigt werden, dass der Zerfall der Polaritonen in MEs schneller
passiert als Thermalisierungen und Streuungen zwischen den SPP-ME-Polaritonen.
- 61 -
Sample 2
Sample 1
0.6
0.5
Fluoreszensintensität [a.u.]
Fluoreszensintensität [a.u.]
0.6
0.4
0.3
0.2
0.1
0.5
0.4
0.3
0.2
0.1
30
40
50
60
70
80
30
90
40
50
60
Θ [ ◦]
Θ [ ◦]
Sample 3
Sample 4
70
80
90
70
80
90
70
80
90
0.6
Fluoreszensintensität [a.u.]
Fluoreszensintensität [a.u.]
0.6
0.5
0.4
0.3
0.2
0.1
0.5
0.4
0.3
0.2
0.1
30
40
50
60
70
80
90
30
40
50
Θ [ ◦]
60
Θ [ ◦]
Sample 5
Sample 6
0.6
0.55
0.5
Fluoreszensintensität [a.u.]
Fluoreszensintensität [a.u.]
0.5
0.4
0.3
0.2
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.1
0.05
30
40
50
60
70
80
90
Θ [ ◦]
30
40
50
60
Θ [ ◦]
Abbildung 12: Fluoreszenz-Wahrscheinlichkeit für die Samples 1 - 6 in Abhängigkeit vom Einfallswinkel.
- 62 -
Kapitel
5
Zusammenfassung
In dieser Arbeit wurde plasmonverstärkte Licht-Molekül-Wechselwirkung in metallischen
Nanostrukturen am Beispiel der Wechselwirkung von Surface Plasmon Polaritonen mit
Sulforhodamin 101 Molekülen untersucht.
Zunächst wurden die Bedingungen, unter denen die Anregung von SPPs mit Licht möglich ist, diskutiert.
Dann wurde für das theoretische Szenario - einer Kretschmann-Konfiguration, bestehend
aus einer Glasschicht, einem 55 Nanometer dicken Silberfilm und einer Luftschicht mit der Transfermatrixmethode die elektromagnetischen Felder und der Poyntingvektor
im Schichtsystem, sowie das Reflektivitätsspektrum berechnet. Anhand der Ergebnisse
wurde die Anregung von SPPs an der Grenzfläche zwischen Silberfilm und Luftschicht
untersucht und ihre Eigenschaften diskutiert.
Um die Wechselwirkung von SPPs mit Sulforhodamin 101 Molekülen zu studieren, wurde
ein zweites Szenario angenommen, eine durch eine 50 Nanometer dicke Moleküle enthaltende Schicht modifizierte Kretschmann-Konfiguration. Die Schicht besteht aus einem
Dielektrikum in der Sulforhodamin 101 Moleküle homogenen verteilt sind. Die Kopplung
zwischen SPPs und den durch die SPPs verursachten Anregungen der Sulforhodamin 101
Moleküle - MEs - führt zu neuen Hybrid-Moden, sogenannten SPP-ME-Polaritonen. Bei
starker Kopplung wird das an der Aufspaltung der Energiedispersion in Dispersionsäste
sichtbar. Um das sowie die Modifikation der Energieniveaus der angeregten Zustände zu
zeigen, wurde die Energiedispersion der Hybridzustände für ein Drei-Niveau-System mit
einem Oszillatormodell berechnet.
Um die Wechselwirkung in Abhängigkeit von der Molekülkonzentration zu untersuchen,
wurden sechs theoretische Szenarien mit steigender Molekülkonzentration behandelt.
Für diese sechs Szenarien wurden die elektromagnetischen Felder, die Poyntingvektoren
und die Reflektivitätsspektren mit der Transfermatrixmethode und die Dispersionen der
Energieeigenwerte mit dem Oszillatormodell berechnet. Um die Stärke der Kopplung in
Abhängigkeit von der Molekülkonzentration zu bestimmen, wurden die Rabiaufspaltung
der Energieeigenwerte und der reflektierten Spektren berechnet. Für alle sechs Szenarien konnte starke Kopplung zwischen den SPPs und den MEs der Sulforhodamin 101
Moleküle gezeigt werden. Für die berechneten Werte war für alle sechs Fälle doppeltes
Rabisplitting zu sehen, beide MEs der Sulforhodamin Moleküle koppeln stark mit den
SPPs. Am Rabisplitting war eine Zunahme der Kopplungsstärke zwischen SPPs und der
Sulforhodaminschicht mit steigender Molekülkonzentration sichtbar. Die berechneten
Werte der Rabisplittings waren etwas höher als die im Rahmen eines Experiments gemessenen Werte. Im Hinblick auf die bei den Rechnungen gemachten Annahmen und der
Messunsicherheit bei der Bestimmung der Rabisplittings sind die Werte jedoch in guter
Übereinstimmung.
Die elektromagnetischen Felder und die Poyntingvektoren, die für die Schichtsysteme mit
verschiedener Molekülkonzentration berechnet wurden, sind in dieser Arbeit nicht alle
aufgeführt. Mit steigender Konzentration wird eine qualitative Veränderung der Felder
und der Poyntingvektoren sichtbar.
Um die Anregung von SPP-ME-Moden weiter zu analysieren, wurde die Energieflussdichte
an der Grenzfläche zwischen Silberfilm und Molekülfilm berechnet. Sie ist proportional zur Anregungs-Wahrscheinlichkeit der SPP-ME-Hybridmoden. Weiters wurde die
Fluoreszenz-Wahrscheinlichkeit, die direkt mit der Besetzung der angeregten Zustände
zusammenhängt, mit einem Drei-Niveau-Oszillator-Modell genähert.
- 64 -
Anhang
A
A.1 Permittivität der Sulforhodamin 101 Schicht
Zur Berechnung der dielektrischen Permittivität der Sulforhodamin Moleküle wird das
Lorentz-Oszillatormodell verwendet. Wie schon erwähnt, haben optische Materialien
im Allgemeinen viele charakteristische Resonanzen, die von Gitterschwingungen und
Oszillationen gebundener Elektronen herrühren. Treten diese an unterscheidbaren Frequenzen auf, d.h. hat ein Molekül i unterscheidbare Absorptionsmaxima, entspricht das
i natürlichen Resonanzfrequenzen, die durch i Lorentzoszillatoren modelliert werden
können. Die Lösung der Lorentzoszillatorgleichung 1.47 ergibt:
x (t ) = −
e
E (t ).
me (ω 0i2 − ω 2 − iγi ω)
Für i Oszillatoren wird die Polarisation damit zu
P=
N e2 X
1
E.
2
me i (ω 0i − ω 2 − iγi ω)
Die Permittivität ist:
ε (ω) = 1 +
N e2 X
1
.
2
ε 0me i (ω 0i − ω 2 − iγi ω)
Sulforhodamin 101 hat zwei Maxima im Absorptionsspektrum. Die Permittivität der
Schicht aus Matrixmaterial und Sulforhodamin 101 Molekülen ist:
ε (ω) = εs +
X
Ai ω 0i2
i
(ω 0i2 − ω 2 − iγi ω)
.
Ai ist der Parameter der Stärke der Oszillation mit Resonanzfrequenz ωi :
Ai =
N e2
.
ω0i2 ϵ0me
Die Permittivität des Matrixmaterials aus Epoxidharz ist εs . Der Dämpfungsparameter γi
entspricht der Halbwertsbreite des jeweiligen Maximums der Absorption.
Für die Glasschicht aus Prisma, Indexmatchingöl und Glassubstrat wurde ein effektiver
Brechungsindex von nд = 1.5 angenommen. Die Werte von nд und εs wurden variiert,
um die kleine Unsicherheit in der Bestimmung des Einfallswinkels zu kompensieren und
eine bestmögliche Übereinstimmung zwischen gemessenen und errechneten Werten zu
bekommen2 .
Tabelle 3 enthält die Parameter aus Ref.[2], die zur Berechnung der Permittivität der
Sulforhodamin 101 Schicht verwendet wurden:
Tabelle 3
Sample εs
nд
A1
A2
γ 1 , eV
γ 2 , eV
ω 1 , eV
ω 2 , eV
SR101, mд
1
2,5
1,605
0,0280
0,00084
0,2
0,07
2,08
2,26
0,3
2
2,7
1,610
0,0365
0,00100
0,2
0,07
2,07
2,25
0,5
3
2,9
1,485
0,0940
0,00650
0,2
0,11
2,06
2,25
1
4
3,0
1,505
0,1330
0,01300
0,2
0,12
2,05
2,24
2
5
3,1
1,485
0,1680
0,01900
0,18
0,12
2,05
2,22
3
6
3,0
1,330
0,2260
0,02900
0,2
0,14
2,05
2,23
4
- 66 -
A.2 Multischichtsystem, Transfermatrixmethode
Um die Reflektivität, die Transmittivität und die elektromagnetischen Felder der in dieser
Arbeit untersuchten Schichtsysteme zu berechnen, wird die Transfermatrixmethode
verwendet.
z
ε
H
H
ε
d2
H
ε
d1
H
H
x
H
H
ε
k
Abbildung 1: Multischichtsystem
Das TM-polarisierte magnetische Feld, in einer Struktur aus vier homogenen und isotropen Schichten mit unterschiedlicher Permittivität, kann wie folgt geschrieben werden:
Hl (x,z,t ) = (0,Hl (z), 0)e ±ikx x e −iωt
H 1 (z) = H +1e ik1z z + H −1e −ik1z z
H 2 (z) = H +2e ik2z z + H −2e −ik2z (z−d1 )
H 3 (z) = H +3e ik3z (z−d1 ) + H −3e −ik3z (z−d2 −d1 )
H 4 (z) = H +4e ik4z (z−d2 −d1 ) .
Aus 1.26 und 1.27 erhält man das TM-polarisierte elektrische Feld. Wendet man die
Stetigkeitsbedingungen aus 1.28 an, kann man für die l-te Grenzfläche schreiben:
H +l e ikl z (z−z+l 0 ) + H −l e −ikl z (z−z −l 0 ) = H +l+1e ikl z (z−z+l 0+1 ) + H −l+1e −ikl z (z−z −l 0+1 )
klz
klz+1
(H +l e ikl z (z−z+l 0 ) − H −l e −ikl z (z−z −l 0 ) =
(H +l e ikl z (z−z+l 0+1 ) − H −l e −ikl z (z−z −l 0+1 ) ).
εl
εl+1
An der ersten Grenzfläche bei z = 0 führt das zu folgendem Gleichungssystem:
- 67 -

1

 
1
1
  H +1  =  k
k 2z
 
 2z
−
H −1  
ε2
ε2
1
 k
 1z
ε1
−
k 1z
ε1



H +1
1
 =
2

H −1
k 2z ε 1
k 2z ε 1
1−
k 1z ε 2
k 1z ε 2
k 2z ε 1
k 2z ε 1
1−
1+
k 1z ε 2
k 1z ε 1



1+






1
0
H
+2



 
0 e ik2zd1   H −2 
1
0
H +2
1
0




 
 0 e ik2zd1   H −2  .
An der zweiten Grenzfläche bei z = d 1 erhält man:
k 3z ε 2
k 3z ε 2
1−
k 2z ε 3
k 2z ε 3
k 3z ε 2
k 3z ε 2
1−
1+
k 2z ε 3
k 2z ε 3


H +2



=
H −2  
e
−ik 2zd1

0
1

0 1 2


1+




H +3


 


 0 e ik3zd2   H −3  .
An der dritten Grenzfläche bei z = d 1 + d 2 gilt:


H +3



=
H −3  
e −ik3zd2 0

1

0 1 2



k 4z ε 3
k 4z ε 3
1−
1+
k 3z ε 4
k 3z ε 4
k 4z ε 3
k 4z ε 3
1+
1−
k 3z ε 4
k 3z ε 4



 H +4
 

 H −4  .
Die Änderung der Amplitude und der Intensität wird beschrieben durch die Matchingmatrizen:
k z εl
k z εl
1 + l +1
1 − l +1

1
kzl εl+1
kzl εl+1
Al = 
k
ε
2  1 − zl +1 l 1 + kzl +1 εl
kzl εl+1
kzl εl+1



.


Die jeweiligen Propagationsmatrizen beschreiben die Phasenänderungen der Wellen über die Grenzflächen zwischen den Schichten:

Pl = 
e −ikzl +1 dl

0
.
0 e ikzl +1 dl 
- 68 -
Die Transfermatrix erhält man dann durch die Multiplikation aller Propagations- und
Matchingmatrizen:
T = A1 P 1A2 P 2A3

H +1


T11 T12


=

H −1   T21 T22  
H +1 = T11H +4
Der Reflexionskoeffizient ist
r=
Der Transmissionskoeffizient ist
H +4


0 
H −1 = T21H +4 .
Hre f (z=0) T21H +4 T21
=
=
.
Hinc (z=0) T11H +4 T11
t=
Htrans (z=d1 +d2 )
H +4
1
=
.
=
Hinc (z=0)
T11H +4 T11
Die Reflektivität ergibt sich mit 1.30 aus dem Reflexionskoeffizienten. Aus dem Transmissionskoeffizienten kann man, da es an der letzten Grenzfläche nur ein aus positiver
z-Richtung transmittiertes Feld gibt,
H 4(z=d1 +d2 ) = H +4 = t,
die Amplituden des Magnetfeldes in den davor liegenden Schichten berechnen24,33,50 .
- 69 -
Literatur
[1] B Auguié, »Optical properties of gold nanostructures«, Diss., University of Exeter,
2009.
[2] S Baieva, »Surface plasmon polariton interaction with Sulforhodamine 101 dye«,
Magisterarb., University of Jyväskylä, 2011.
[3] SV Baieva, TK Hakala et al., »Strong coupling between surface plasmon polaritons
and Sulforhodamine 101 dye«, »Nanoscale Research Letters«, Bd. 7, Nr. 1, 191,
2012.
[4] S Balci, C Kocabas et al., »Tuning surface plasmon-exciton coupling via thickness
dependent plasmon damping«, »Phys. Rev. B«, Bd. 86, Nr. 23, 235402, 2012.
[5] J Bellessa, C Bonnand et al., »Strong Coupling between Surface Plasmons and
Excitons in an Organic Semiconductor«, »Phys. Rev. Lett.«, Bd. 93, Nr. 3, 036404,
2004.
[6] M Born, E Wolf et al., »Principles of Optics«, New York: Cambridge University
Press, 2003.
[7] N Cade, T Ritman-Meer et al., »Strong coupling of localized plasmons and
molecular excitons in nanostructured silver films«, »Phys. Rev. B«, Bd. 79, Nr. 24,
241404, 2009.
[8] T Davis, »Surface plasmon modes in multi-layer thin-films«, »Opt. Commun.«,
Bd. 282, Nr. 1, 135, 2009.
[9] I De Leon, P Berini, »Amplification of long-range surface plasmons by a dipolar
gain medium«, Diss., Ottawa-Carleton Institute for Electrical und Computer
Engineering, 2010.
[10] M Fox, »Optical Properties of Solids«, New York: Oxford University Press, 2001.
[11] SV Gaponenko, »Introduction to Nanophotonics«, New York: Cambridge
University Press, 2009.
[12] T Hakala, J Toppari et al., »Vacuum Rabi Splitting and Strong-Coupling Dynamics
for Surface-Plasmon Polaritons and Rhodamine 6G Molecules«, »Phys. Rev. Lett.«,
Bd. 103, Nr. 5, 053602, 2009.
[13] NJ Halas, »Plasmonics: An Emerging Field Fostered by Nano Letters«, »Nano
Letters«, Bd. 10, Nr. 10, 3816, 2010.
[14] C Hettich, »Coherent Optical Dipole Coupling of Two Individual Molecules at
Nanometre Separation«, Diss., Universität Konstanz
Mathematisch-Naturwissenschaftliche Sektion Fachbereich Physik, 2002.
[15] A Hohenau, »Lichtleitung mit metallischen Nanostrukturen«, Diss., Univerität
Graz, 2004.
[16] S Horstmeier, »Aufbau eines Oberflächenplasmonenresonanz-Biosensors«,
Magisterarb., Universität Bielefeld, 2008.
[17] JD Joannopoulos, SG Johnson et al., »Photonic Crystals: Molding the Flow of
Light (Second Edition)«, Princeton: Princeton University Press, 2008.
[18] P Johnson, R Christy, »Optical Constants of the Noble Metals«, »Phys. Rev. B«,
Bd. 6, Nr. 12, 4370, 1972.
[19] MA Koponen, U Hohenester et al., »Absence of mutual polariton scattering for
strongly coupled surface plasmon polaritons and dye molecules with a large
Stokes shift«, »Phys. Rev. B«, Bd. 88, Nr. 8, 085425, 2013.
[20] A Kuzyk, M Pettersson et al., »Molecular coupling of light with plasmonic
waveguides«, »Optics Express«, Bd. 15, Nr. 16, 9908, 2007.
[21] JR Lakowicz, MH Chowdhury et al., »Plasmon-controlled fluorescence: A new
detection technology«, »Proc. SPIE«, Bd. 6099, 609909, 2006.
[22] EK Lindmark, AV Kavokin et al., »Three coupled oscillators: normal mode
coupling in a microcavity with two different quantum wells«, »Opt. Lett.«, Bd. 21,
Nr. 13, 994, 1996.
[23] SA Maier, »Plasmonics: Fundamentals and Applications«, New York: Springer US,
2007.
[24] M Maksimovic, »Optical resonances in multilayer structures«, Diss., 2008.
[25] M Marder, »Condensed Matter Physics«, Hoboken: Wiley, 2010.
[26] S Mendach, M Bröll, »Oberflächenplasmonen«, Institut für Angewandte Physik,
Universität Hamburg, 2008.
- 71 -
[27] WL Mochán, »Plasmons«, Centro de Ciencias Físicas, Universidad Nacional
Autónoma de México, Cuernavaca, 2004.
[28] RJ Moerland, TK Hakala et al., »Vacuum Rabi splitting for surface plasmon
polaritons and Rhodamine 6G molecules«, »Proc. SPIE«, Bd. 8070, 80700D, 2011.
[29] WA Murray, »Optical properties of nanoscale silver structures fabricated by
nanosphere lithography«, Diss., University of Exeter, 2005.
[30] N Nagarajan, G Paramaguru et al., »Photosensitization of Colloidal SnO2
Semiconductor Nanoparticles with Xanthene Dyes«, »Journal of Chemistry«,
Bd. 2013, Nr. 585920 2013.
[31] L Novotny, »Strong coupling, energy splitting, and level crossings: A classical
perspective«, »Am. J. Phys.«, Bd. 78, Nr. 11, 1199, 2010.
[32] L Novotny, B Hecht, »Principles of Nano-Optics«, New York: Cambridge
University Press, 2006.
[33] SJ Orfanidis, »Electromagnetic Waves and Antennas«, Piscataway: Rutgers
University, 2008.
[34] SA Ramakrishna, AD Armour, »Propagating and evanescent waves in absorbing
media«, »Am. J. Phys.«, Bd. 71, Nr. 6, 562, 2003.
[35] M Sauer, J Hofkens et al., »Handbook of Fluorescence Spectroscopy and Imaging«,
Weinheim: Wiley, 2011.
[36] F Schertz, »Nahfeld-induzierte Elektronenemissions-Mikrospektroskopie an stark
gekoppelten Plasmonen und metallischen Mikrostrukturen«, Diss., Mainz:
Johannes Gutenberg-Universität, 2013.
[37] RP Schumann, S Gregory, »Near-Field Modification of Interference Components
in Surface Plasmon Resonance«, »arXiv:0804.3418v1 [physics.optics]« 2008.
[38] S Schwieger, P Vasa et al., »Surface plasmon polariton-exciton interaction in
metal-semiconductor and metal-dye nanostructures«, »Journal of Physics:
Conference Series«, Bd. 210, 012001, 2010.
[39] J Seidel, »Propagation, scattering and amplification of surface plasmons in thin
silver films«, Diss., Technische Universität Dresden, 2005.
[40] E Sommer, »Ultrakurzzeitdynamik von Molekül/Metall-Hybridnanostrukturen«,
Magisterarb., Carl von Ossietzky Universität Oldenburg, 2012.
[41] VJ Sorger, RF Oulton et al., »Toward integrated plasmonic circuits«, »MRS
Bulletin«, Bd. 37, Nr. 08, 728, 2012.
[42] C Symonds, C Bonnand et al., »Particularities of surface plasmon–exciton strong
coupling with large Rabi splitting«, »New Journal of Physics«, Bd. 10, Nr. 6,
065017, 2008.
- 72 -
[43] D Timmers, W Woodruff, »Modeling Electromagnetic Wave Interactions with
Nanostructures in Plasmonic Devices«, 2011.
[44] P Törmä, WL Barnes, »Strong coupling between surface plasmon polaritons and
emitters«, »Invited review article submitted to Reports on Progress in Physics«
2014.
[45] P Vasa, R Pomraenke et al., »Coherent Exciton–Surface-Plasmon-Polariton
Interaction in Hybrid Metal-Semiconductor Nanostructures«, »Phys. Rev. Lett.«,
Bd. 101, Nr. 11, 116801, 2008.
[46] P Vasa, W Wang et al., »Real-time observation of ultrafast Rabi oscillations
between excitons and plasmons in metal/molecular aggregate hybrid
nanostructures«, »EPJ Web of Conferences«, Bd. 41, 09018, 2013.
[47] W Wang, P Vasa et al., »Interplay between Strong Coupling and Radiative
Damping of Excitons and Surface Plasmon Polaritons in Hybrid Nanostructures«,
»ACS Nano«, Bd. 8, Nr. 1, 1056, 2014.
[48] J White, »Surface Plasmon Polaritons«,
[http://large.stanford.edu/courses/2007/ap272/white1/ (Online; Stand 6. Oktober
2014)], 2007.
[49] Wikipedia, »Polariton — Wikipedia, Die freie Enzyklopädie«, [Online; Stand 6.
Oktober 2014], 2013.
[50] P Yeh, »Optical Waves in Layered Media«, New York: Wiley-Interscience, 2005.
[51] AV Zayats, II Smolyaninov et al., »Nano-optics of surface plasmon polaritons«,
»Physics Reports«, Bd. 408, Nr. 3-4, 131–314, 2005.
- 73 -
Danksagung
An dieser Stelle möchte ich all jenen danken, die durch ihre fachliche und persönliche
Unterstützung zum Gelingen dieser Diplomarbeit beigetragen haben.
Herrn Ao. Univ. Prof. Dr. Ulrich Hohenester möchte ich für die Betreuung meiner
Diplomarbeit danken.
Meinen Eltern und meinen Freunden möchte ich für den liebevollen Rückhalt und
Zuspruch Danken.
Einen ganz besonderen Dank möchte ich Mo, Andi und Kathi aussprechen.