Zahlen Zahlen

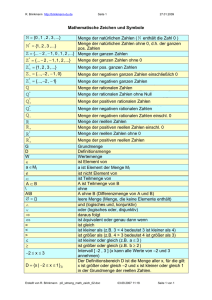
Zahlen
Ulrich Görtz, [email protected]
Der Begriff der Zahl ist schon sehr alt, und hat sich im Lauf der Geschichte immer wieder gewandelt. Der Gebrauch von Zahlen geht heutzutage auch im Alltag weit über
das Zählen hinaus. Auf diesem Poster werden die natürlichen, die ganzen, die rationalen, die reellen und die komplexen Zahlen vorgestellt.
Die natürlichen Zahlen N
Die komplexen Zahlen C
Als die natürlichen Zahlen bezeichnet man die Zahlen 1, 2, 3, ... .
Oft wird auch die 0 als natürliche Zahl bezeichnet, auch wenn
das Konzept, 0 als eine Zahl zu betrachten viel später entstanden ist als das Abzählen. Im antiken Griechenland war die Null
nicht bekannt. In Indien hat sich die Null als Zahlzeichen zwischen 300 und 600 n. Chr. etabliert. Selbst in dem einflussreichen Buch Liber abaci von L. Fibonacci, das um 1200 in Italien erschien, tritt die Null zwar als “Zeichen” auf, ist aber nicht
gleichberechtigt mit den anderen Zahlen. Die Verwendung der
Null beim Rechnen setzte sich erst im 17. Jahrhundert durch.
Ist x eine reelle Zahl, so ist ihr Quadrat x 2 größer oder gleich 0. Die Gleichung X 2 = −1 ist also in
den reellen Zahlen nicht lösbar. Man kann den Zahlbereich R der reellen Zahlen erweitern zu einem
größeren Bereich C, in dem man ähnlich wie mit reellen Zahlen rechnen (addieren, subtrahieren,
multiplizieren, dividieren) kann, und in dem es ein Element i ∈ C gibt, dessen Quadrat gleich −1 ist:
i 2 = −1.
Wir definieren dazu
C = {(x, y ); x, y ∈ R}
als die Menge aller Paare von reellen Zahlen mit den folgenden Rechenregeln:
(x, y) + (x 0, y 0) := (x + x 0, y + y 0)
(x, y ) − (x 0, y 0) := (x − x 0, y − y 0)
(x, y) · (x 0, y 0) := (xx 0 − yy 0, xy 0 + yx 0)
Der Mathematiker L. Kronecker (1823-91) schrieb Die ganzen Zahlen
hat der liebe Gott gemacht, alles andere ist Menschenwerk.
Die ganzen Zahlen Z
Addiert man zwei natürliche Zahlen, so erhält man wieder eine
natürliche Zahl. Subtrahieren kann man dagegen im Bereich der
natürlichen Zahlen nicht immer: Dem Ausdruck 3 − 5 kann man
im Bereich der natürlichen Zahlen keinen Sinn verleihen.
Durch Hinzufügen der Negativen −1, −2, −3, ... erhält man aus
den natürlichen Zahlen die Menge der ganzen Zahlen. Hier sind
nun Addition, Subtraktion und Multiplikation definiert.
Negative Zahlen wurden wohl in China, und womöglich auch in
Indien, schon vor ca. 2000 Jahren benutzt. Im alten Griechenland war dieses Konzept nicht bekannt. G. W. Leibniz (16461716) war der erste europäische Mathematiker, der die negativen Zahlen systematisch berücksichtigt hat.
Die rationalen Zahlen Q
Die Menge Q besteht aus allen Zahlen, die als Bruchzahlen ba
darstellbar sind. Hier sind a und b ganze Zahlen, wobei b 6= 0.
Rationale Zahlen kann man addieren, subtrahieren und multiplizieren. Außerdem kann man durch alle rationalen Zahlen 6= 0
auch dividieren. Dabei gelten die “üblichen Rechenregeln” —
man bezeichnet daher die Menge Q mit diesen Rechenoperationen als einen Körper.
Der Übergang von den ganzen zu den rationalen Zahlen ist konzeptionell viel komplizierter als der von den natürlichen zu den
ganzen Zahlen. Ein wesentlicher Grund dafür ist, dass die gleiche rationale Zahl durch verschiedene Bruchdarstellungen repräsentiert werden kann:
2 4 24
= = .
3 6 36
√
(Die Division ist etwas komplizierter und wird im folgenden nicht mehr benötigt.)
Die Menge C (mit diesen Rechenoperationen) heißt die Menge der komplexen Zahlen. Ist x ∈ R, so
identifizieren wir x mit der komplexen Zahl (x, 0). Damit gilt zum Beispiel 0 + z = z und 1 · z = z für
alle komplexen Zahlen z. Mit der Definition
i := (0, 1) ∈ C
gilt nach den obigen Regeln dann tatsächlich
i 2 = (0 · 0 − 1 · 1, 0 · 1 + 1 · 0) = (−1, 0) = −1.
Mit diesen Rechenregeln haben wir
x + yi = (x, y)
und man schreibt für komplexe Zahlen meist x + yi statt (x, y).
t und
Der Begriff der komplexen Zahl hat sich seit ca. 1550 entwickel
gewurde um 1800 auf eine auch aus heutiger Sicht akzeptable Basis
Mastellt. Seitdem gehört er zum unabdingbaren Handwerkszeug der
hafthematiker und hat auch viele Anwendungen in anderen Wissensc
ten, insbesondere der Physik.
Die Menge R der reellen Zahlen besteht, etwas salopp gesagt,
aus allen Zahlen, die eine Dezimalbruchdarstellung besitzen, die
also durch die Ziffern 0 bis 9 und Vor- und Nachkommateil “geschrieben” werden können. Der Nachkommateil darf dabei auch
unendlich lang sein. Auch hier gibt es wieder das Phänomen,
dass verschiedene Dezimalbruchdarstellungen die gleiche Zahl
darstellen können.
Man kann die reellen Zahlen durch einen systematischen Prozess ausgehend von den rationalen Zahlen konstruieren. Die erste “wasserdichte” Definition der reellen Zahlen wurde 1871 von
G. Cantor gegeben.
Wir können die reellen Zahlen mit den Punkten auf dem “Zahlenstrahl” identifizieren. Die meisten dieser Punkte sind nicht als
Bruchzahl darstellbar. Auch ausgehend von rationalen Zahlen
lassen sich leicht Fragestellungen formulieren, die innerhalb der
rationalen Zahlen nicht behandelt werden können — zum Beispiel ist die Länge
der Diagonale eines Quadrats mit Seitenlän√
ge 1 gerade 2 — die Quadratwurzel von 2, und diese ist keine
rationale Zahl.
Jedes Polynom X n + an−1X n−1 +
· · · + a1X + a0 (mit n ≥ 1) besitzt
eine Nullstelle in C. Man sagt, der
Körper der komplexen Zahlen sei
algebraisch abgeschlossen.
Die komplexe Zahlenebene
Betrachten wir die komplexen Zahlen wie in der Definition als Paare reeller Zahlen, so können wir sie
als Punkte in der Ebene —gegeben durch x- und y-Koordinate— ansehen. Zum Beispiel entspricht
die Zahl −2 + 2i dann dem Punkt mit Koordinaten (−2, 2) im linken oberen Quadranten. Der reelle
“Zahlenstrahl” ist als die x-Achse in die komplexe Ebene eingebettet.
−2 + 2i = (1 + i)3
2i = (1 + i)2
i
1+i
1
2 ist nicht rational. Gäbe es nämlich eine Bruchzahl ba mit teilerfremden ganzen Zahlen a und b und
2
a
2 = 2b 2. Also ist a2 und damit auch a gerade. Also ist a2 sogar durch 4 teilbar, so
=
2,
so
hätten
wir
a
b
dass auch b gerade sein muss. Dann sind aber a und b doch nicht teilerfremd — ein Widerspruch!
Die reellen Zahlen R
für alle x, y ∈ R,
−2 − i
Gibt es noch größere Zahlbereiche?
Den Übergang von R zu C kann man etwas verkürzt auch so beschreiben: Man führt ein zusätzliches
Symbol i ein mit i 2 = −1 und rechnet ansonsten mit den üblichen Rechenregeln. Insofern ist es eine
naheliegende Frage, ob man die kompexen Zahlen ihrerseits durch die Hinzunahme endlich vieler
zusätzlicher Symbole zu noch größeren Zahlbereichen erweitern kann.
Man kann zeigen, dass das nicht möglich ist, wenn man festlegt, dass die “üblichen Rechenregeln”
weiterhin gelten sollen.
Verzichtet man aber auf einzelne Rechenregeln, so kann man tatsächlich noch größere Zahlbereiche
definieren. Zum Beispiel die Quaternionen (erstmals gefunden 1843 von W. Hamilton), in denen aber
die Produkte xy und yx nicht unbedingt gleich sind.
Ein noch größerer Zahlbereich sind die Oktonionen, in denen im allgemeinen (xy )z und x(yz) verschieden sind.
Neben diesen Erweiterungen der rationalen Zahlen spielen, besonders in der Zahlentheorie, noch
andere “Körper” eine Rolle, also Mengen von Zahlen, für die die Rechenoperationen Addition, Subtraktion, Multiplikation und Division (durch Zahlen 6= 0) definiert sind. Ein Beispiel ist (für eine Primzahl p) der endliche Körper mit p Elementen: Als Menge ist er gegeben als {0, 1, ... , p − 1}. Die
Summe zweier Elemente x und y wird wie folgt gebildet: Zuerst addiert man x und y als ganze Zahlen, dann bildet man den Rest bei Division durch p. Ist zum Beispiel p = 7, so ist 5 + 6 = 4, denn 4
ist der Rest von 11 bei Division durch 7. Analog erfolgen Subtraktion und Multiplikation (im Beispiel:
5 − 6 = 6, 5 · 6 = 2). Die Division ist nicht so leicht zu beschreiben, ist aber immer möglich.
LATEX Tik Zposter