Zahlen in der Stellenwerttafel

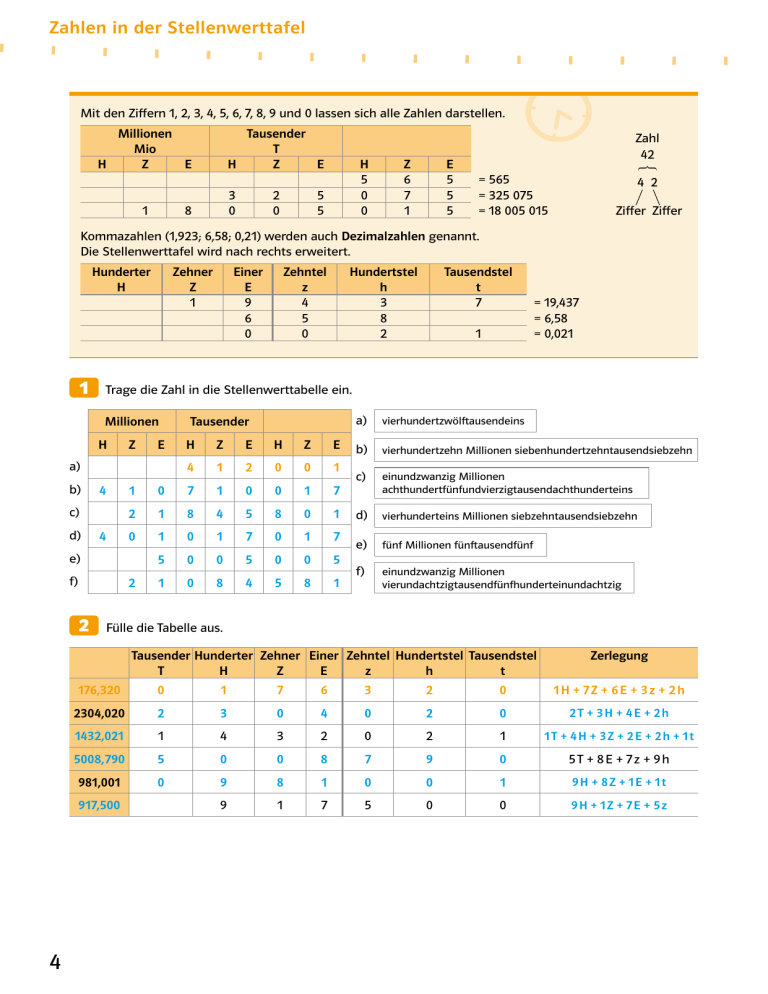
Zahlen in der Stellenwerttafel
Mit den Ziffern 1, 2, 3, 4, 5, 6, 7, 8, 9 und 0 lassen sich alle Zahlen darstellen.
Millionen
Mio
H
Z
E
1
Tausender
T
H
Z
E
3
0
8
2
0
H
5
0
0
5
5
Z
6
7
1
E
5
5
5
Zahl
42
64870
4 2
= 565
= 325 075
= 18 005 015
Ziffer Ziffer
Kommazahlen (1,923; 6,58; 0,21) werden auch Dezimalzahlen genannt.
Die Stellenwerttafel wird nach rechts erweitert.
Hunderter
H
1
Zehner
Z
1
H
Z
E
a)
4
c)
d)
Hundertstel
h
3
8
2
4
f)
Tausender
H
Z
E
H
Z
E
4
1
2
0
0
1
1
0
7
1
0
0
1
7
2
1
8
4
5
8
0
1
0
1
0
1
7
0
1
7
5
0
0
5
0
0
5
1
0
8
4
5
8
1
e)
2
2
Zehntel
z
4
5
0
Tausendstel
t
7
1
= 19,437
= 6,58
= 0,021
Trage die Zahl in die Stellenwerttabelle ein.
Millionen
b)
Einer
E
9
6
0
a)
vierhundertzwölftausendeins
b)
vierhundertzehn Millionen siebenhundertzehntausendsiebzehn
c)
einundzwanzig Millionen
achthundertfünfundvierzigtausendachthunderteins
d)
vierhunderteins Millionen siebzehntausendsiebzehn
e)
fünf Millionen fünftausendfünf
f)
einundzwanzig Millionen
vierundachtzigtausendfünfhunderteinundachtzig
Fülle die Tabelle aus.
Tausender Hunderter Zehner Einer Zehntel Hundertstel Tausendstel
T
H
Z
E
z
h
t
176,320
0
1
7
6
3
2
0
1 H + 7 Z + 6 E + 3 z + 2 h
2304,020
2
3
0
4
0
2
0
2 T + 3 H + 4 E + 2 h
1432,021
1
4
3
2
0
2
1
1 T + 4 H + 3 Z + 2 E + 2 h + 1 t
5008,790
5
0
0
8
7
9
0
5 T + 8 E + 7 z + 9 h
981,001
0
9
8
1
0
0
1
9 H + 8 Z + 1 E + 1 t
9
1
7
5
0
0
9 H + 1 Z + 7 E + 5 z
917,500
4
Zerlegung z
Zahlen auf dem Zahlenstrahl
Auf einem Zahlenstrahl werden die Zahlen der Größe nach angeordnet.
–6
–5
–4
–3
–2
–1
negative Zahlen
0
+1
+2
+3
positive Zahlen
+4
+5
+6
Auf dem Zahlenstrahl werden
die Zahlen von links nach
rechts immer größer:
Auch Dezimalzahlen lassen sich darstellen. Dazu muss der Zahlenstrahl
in weitere Einheiten unterteilt werden.
–4
–6
–5
1
–4
– 2,5
–3
– 0,7
–2
+ 0,5
–1
0
+ 2,4
+1
+2
+ 4,5
+3
+4
+5
+6
– 80
– 40
– 100 10
40
0 – 50 b) –1,1
– 0,8
85
50
– 0,4
– 1 2
– 20
0,1
100
0,5
2. Zahlenstrahl zeichnen.
chnen.
3. Markierungen einzei
4. Zahlen eintragen.
0,95
0 – 1 steht rechts von – 6,
also – 1 > – 6 („ist größer als“).
Zahlenstrahl zeichnen
ahls
1. Länge des Zahlenstr
ten
hei
Ein
und Länge der
B.
z.
n,
me
bestim
1 Einheit š 1 cm
1 Einheit š 5 cm …
Auf welche Zahlen zeigen die Pfeile?
a)
– 3 steht links von + 2,
also – 3 < + 2 („ist kleiner als“).
1
Vergleiche die Zahlen. Schreibe < oder > in das Kästchen.
a) – 6
<
–4
b) 7
>
–3
c)
–5
d) – 1,5 <
– 0,5
e) 0,7
<
2,4
f) – 5,7
>
– 7,5
g) 1,3 > – 3,1
h) – 0,1 >
0,01
2 >
> bedeutet: ist größer als
< bedeutet: ist kleiner als
3
a)
Zeichne einen Zahlenstrahl und trage die vorgegebenen Zahlen ein.
–7
– 7
– 7
b)
2
– 5,5
– 4
– 3
– 4
– 3
– 6
25
– 5
– 30
– 30
– 30
20
– 15
– 20
–4
–3
4,5
– 1,5
– 2
0
– 1
0
5
– 15
– 10
0
– 10
0
– 5,5
–1,5
0
3
2
1
0
5
10
4,5
2
3
4
20
25
5
– 10
20
30
5
z
Runden von Zahlen
1
Entscheide, ob das Runden hier
sinnvoll ist.
ja
nein
Das Auto kostet 20 199 Euro.


Das Haus hat die Hausnummer 199.


Island hat 293 292 Einwohner.


Jesus Christus hatte 12 Apostel.


Der Weltrekord für 100 m Sprint der
Herren beträgt 9,77 Sekunden.


Der Kleinwagen wiegt 815,9 kg.


Die Ziffer rechts von der Rundungsstelle
ist entscheidend.
• bei 0, 1, 2, 3 oder 4, wird abgerundet.
• bei 5, 6, 7, 8 oder 9, wird aufgerundet.
auf Zehner:
auf Hunderter:
auf Tausender:
Beim Runden von Dezimalzahlen gelten die
gleichen Regeln:
auf Zehntel:
36,472 ≈ 36,5 (aufgerundet)
auf Hundertstel:
36,472 ≈ 36,47 (abgerundet)
Das Zeichen
2
≈ bedeutet „ist ungefähr“.
Runde.
a)
6 546
21 496
3 458
96 437
auf Zehner
6 550
21 500
3 460
96 440
auf Hunderter
6 500
21 500
3 500
96 400
auf Tausender
7 000
21 000
3 000
96 000
658 725
94 800
209 500
49 957
auf Tausender
659 000
95 000
210 000
50 000
auf Zehntausender
660 000
90 000
210 000
50 000
auf Hunderttausenderer
700 000
100 000
200 000
0
b)
3 Runde die Einwohnerzahlen auf Millionen
mit zwei Nachkommastellen und sortiere die
Städte nach ihrer Größe.
Hamburg
6
21 235 ≈ 21 240 (aufgerundet)
21 235 ≈ 21 200 (abgerundet)
21 235 ≈ 21 000 (abgerundet)
Einwohnerzahl gerunde
t
Rang
Stadt
Einwohner in Mio.
1
Berlin
3,39
2
Hamburg
1,73
3
München
1,25
4
Köln
0,97
1 734 830
Berlin
1,73
3 387 828
Dortmund
3,39
588 680
Stuttgart
0,59
591 657
5
Stuttgart
0,59
München
0,59
1 249 176
Dresden
1,25
6
Dortmund
0,59
487 421
Köln
0,49
969 709
7
Leipzig
0,50
Leipzig
0,97
498 491
0,50
8
Dresden
0,49
z
Schätzen und überschlagen
1
Nicht immer ist es möglich, eine
Größe genau anzugeben. Eine ungefähre
Vorstellung erhält man durch schätzen.
Schätze das Gewicht der Tiere und ordne die
passenden Gewichte zu.
Elefant
750 kg
Blaumeise
5t
Kuh
60 kg
Katze
10 g
Schaf
8 kg
z
2
Welche orange Strecke ist länger, die obere
oder die untere? Schätze zunächst und miss dann.
a)
b)
Beide Strecken sind gleich lang.
Eine Rechnung mit gerundeten Zahlen heißt Überschlagsrechnung.
Gerundete Zahlen geben nur ein ungefähres Ergebnis, lassen sich aber leichter
im Kopf zusammenrechnen.
Aufgabe: 1 376 + 712 = 2088
713 – 89 = 624
Überschlag: 1 400 + 700 ≈ 2 100
700 – 100 ≈ 600
3
Führe eine Überschlagsrechnung durch.
b) 811 – 385 ≈ 800 – 400 ≈ 400
c) 87 + 52 + 79 ≈ 90 + 50 + 80 ≈ 220
d) 471 + 288 ≈ 500 + 300 ≈ 800
e) 2 783 – 219 ≈ 2 800 – 200 ≈ 2 600
f) 7 078 – 4 139 ≈ 7 000 – 4 000 ≈ 3 000
g) 82 + 58 + 71 ≈ 80 + 60 + 70 ≈ 210
h) 72 652 + 21 675 ≈ 73 000 + 22 000 ≈ 95 000
a) 83 + 47
4
≈ 80 + 50 ≈ 130
Kontrolliere mit einer Überschlagsrechnung, ob das Ergebnis stimmen kann oder eindeutig falsch ist.
Aufgabe
Überschlagsrechnung
kann stimmen/falsch
a) 729 + 582 + 433 = 1 744
700 + 600 + 400 = 1 700
kann stimmen
b) 8 971 – 1 893 = 8 078
9 000 – 2 000 = 7 000
falsch
c) 95 + 634 + 178 = 907
100 + 600 + 200 = 900
kann stimmen
d) 827 + 386 + 507 = 1 720
800 + 400 + 500 = 1 700
kann stimmen
e) 7 856 – 5 972 = 3 884
8 000 – 6 000 = 2 000
falsch
f) 8 329 – 718 = 7 611
8 000 – 1 000 = 7 000
kann stimmen
7
Kopfrechnen: Addieren und subtrahieren
Addieren (+)
Subtrahieren (–)
Summand plus Summand = Summe
1222223444445 12325 1222223444445 12222344445
48
+
37
= 85
Minuend minus Subtrahend = Differenz
122222344445 1223245 122222234444445 12222344445
85
–
37
= 48
1 Zerlege die Aufgabe so, dass du im Kopf
rechnen kannst. Hinweis: Hier gibt es unterschiedliche Lösungswege!
a) 78 + 33
2
Rechne von außen nach innen.
+ 17
= 78 + 2 + 31 = 111
= 91 – 1 – 26 = 64
b) 91 – 27
– 9
423
b) 618 + 33 = 618 + 2 + 31 = 651
288
– 249
32
146
– 23
55
+ 23
– 212
286
Berechne im Kopf.
498
a) 75 + 28
=
103
b) 67 + 25
=
92
c) 49 + 43
=
92
d) 87 – 34
=
53
e) 154 + 38
=
192
f) 237 – 52
=
185
g) 486 + 52
=
538
h) 795 – 67
=
728
i) 89 + 56
=
145
j) 67 + 48
=
115
k) 91 + 75
=
166
l) 143 – 72
=
71
m)347 + 74
=
421
n) 831 + 87
=
918
o) 347 – 76
=
271
p) 671 – 88
=
583
q) 433 + 106 =
539
r) 788 + 203 =
991
s) 522 – 104 =
418
t) 677 – 102 =
575
u) 844 – 295 =
549
4
Knacke die Zahlenmauern. Zwei benachbarte Steine addiert ergeben das Ergebnis darüber.
200
211
121
71
49
8
+ 67
+ 16
– 46
e) 553 + 26 = 553 + 20 + 6 = 579
3
39
100
309
d) 243 – 29 = 243 – 23 – 6 = 214
431
+ 114
– 21
c) 227 + 54 = 227 + 3 + 51 = 281
440
50
22
143
90
40
28
123
12
108
147
20
15
42
37
5
65
82
57
32
13
25
40
29
11
14
Schriftliches Addieren (+)
Beispiel: 6147 + 909
6
1. Schritt: Zahlen stellengerecht untereinander
schreiben.
2. Schritt: Stellenweise berechnen (in der rechten Spalte
beginnen) und Übertrag notieren.
3. Schritt: Das Ergebnis doppelt unterstreichen.
+
3 4 5
+ 4 5 2
7 8 1 2 1 6
b)
9
0
5
Übertrag
1
6
Ü: 6 000 + 1 000 = 7 000
Ergebnis kann stimmen.
+
7 8 3 5 2 7
c)
+
1
Ü:
7 8 3
4 4 9
d)
+
1
1
1
7 9 7
9 9 7
1 3 1 0
1 2 3 2
8 0 0
Ü: 1 0 0 0
Ü: 1 3 0 0
Ü: 1 2 0 0
4 0 7 4 +
8 5
8 9 4 7 6 5 1 8
f)
+
1
2
7
0
Löse die Aufgaben der Reihe nach. Berechne zur Kontrolle den Überschlag.
a)
e)
4
1
7
Mit einer Überschlagsrechnung kannst du das Ergebnis kontrollieren.
1
1
9
1
g)
1
5 4 9 3 +
8 3 7
1
1
h)
1
6 4 0 8
+ 2 7 7 6
1
1
4 1 5 9
1 5 4 6 5
6 3 3 0
9 1 8 4
Ü: 4 2 0 0
Ü: 1 5 5 0 0
Ü: 6 3 0 0
Ü: 9 2 0 0
Schreibe die Aufgaben stellengerecht untereinander und berechne.
a) 7 076 + 5 673 + 113
b) 860 + 5 071 + 1 405
c) 809 + 4 826 + 1 435
d) 7 210 + 847 + 3 528
7 2 1 0 8 0 9 7 0 7 6 8 6 0 + 5 6 7 3
+
1 1 3
1
1
1
2
1
1
2
1
1 1 5 8 5
7 0 7 0
7 3 3 6
1 2 8 6 2
+
8 4 7
+ 3 5 2 8
+ 4 8 2 6
+ 1 4 3 5
+ 5 0 7 1
+ 1 4 0 5
e) 8 973 + 3 142 + 12
f) 9 002 + 4 890 + 422
g) 7 166 + 1 465 + 2 976
h) 9 678 + 2 374 + 173
7 1 6 6
8 9 7 3
9 0 0 2
9 6 7 8
+ 1 4 6 5
+ 3 1 4 2
+ 4 8 9 0
+ 2 3 7 4
+ 2 9 7 6
+
1 2
+
4 2 2
+
1 7 3
1
1
1
1 2 1 2 7
3
a)
1
1
2
1
1
1 1 6 0 7
1 4 3 1 4
2
1
1 2 2 2 5
Welche Zahlen musst du in die Felder einsetzen?
6 7 8
+ 2 1 3 2
+ 1 3 0 0
1
1
1
4 1 1 0
b)
3 6 4
+ 1 7 5 9
1
1
1
2 1 2 3
c)
7 9 8
+ 1 3 0 4
+ 4 1 2 1
1
1
1
6 2 2 3
d)
8 6 8
+ 1 3 0 9
+ 4 4 2 1
1
1
6 5 9 8
9
Schriftliches Subtrahieren (–)
1. Schritt: Zahlen stellengerecht untereinander
schreiben.
2. Schritt: Stellenweise ergänzen, zuerst die Einer,
dann die Zehner, Hunderter…
Übertrag notieren.
3. Schritt: Das Ergebnis doppelt unterstreichen.
Beispiel: 7219 – 587
Mit der Überschlagsrechnung kannst du dein
Ergebnis kontrollieren.
Ü: 7 200 – 600 = 6 600
Ergebnis kann stimmen.
1
a)
–
1
2
1
9
5
8
7
3
2
Beispiel: 778 – 623 – 176
1
6
6
9
7
8
–
6
2
3
–
1
7
6
1
1
1
7
Ü: 1 000 – 600 – 200 = 200
Ergebnis kann stimmen.
Berechne und kontrolliere mit dem Überschlag.
8 7 5 – 2 4 3
9 4 7 – 7 3 6
b)
c)
8 7 4 9 – 5 9 3 8
d)
9 4 3 6 7
– 9 3 4 3 7
1
6 3 2
2 1 1
2 8 1 1
Ü: 7 0 0
Ü: 2 0 0
Ü: 3 0 0 0
b) 903 – 485
9 4 9 – 5 4 7
4 0 2
f) 8 756 – 2 142 – 3 513
c) 7 563 – 3 841
9 0 3 – 4 8 5
1
4 1 8
1
1
3 7 2 2
g) 7 865 – 2 973 – 1 094
2
e) 86 732 – 12 906
8 6 7 3 2
– 1 2 9 0 6
1
1
1
6 8 8
7 3 8 2 6
h) 8 087 – 2 308 – 3 670
i) 7 564 – 658 – 1 056
7 8 6 5 – 2 9 7 3
– 1 0 9 4
1
8 0 8 7 – 2 3 0 8
– 3 6 7 0
1
1
3 7 9 8
7 5 6 4
–
6 5 8
– 1 0 5 6
1
1
1
1
2 1 0 9
5 8 5 0
1 3 9 5 6 7
– 1 0 1 0 1 0
–
5 3 7 0
8 9 7 5 3 3
– 1 2 0 1 5 9
– 7 6 0 2 3 1
Berechne und runde das Ergebnis.
Berechnung:
Runde das
Ergebnis
I. auf 100er
II. auf 1 000er
III. auf 10 000er
10
8 1 2 6
– 7 4 3 8
1
3 1 0 1
3
1 0 0 0
Ü:
d) 8 126 – 7 438
7 5 6 3
– 3 8 4 1
1
8 7 5 6 – 2 1 4 2
– 3 5 1 3
9 3 0
Schreibe die Aufgaben stellengerecht untereinander und berechne.
a) 949 – 547
im Kopf stellenweise addieren
und zur oberen
Zahl ergänzen
9
1
2
1222223422245
7
2 3 7 6 6
– 1 2 4 8 7
–
6 5 7 8
1
1
1
1
4 7 0 1
4 7 0 0
5 0 0 0
0
1
3
3
3
3
3
3
3
0
1
2
0
0
8
0
0
0
7
0
0
0
1
1
1
2
7
7
7
0
1
1
1
1
0
0
4
0
0
0
3
0
0
0
z
Dezimalzahlen schriftlich addieren und subtrahieren
Dezimalzahlen (Kommazahlen) müssen beim
schriftlichen Rechnen stellengerecht untereinander
geschrieben werden.
• Komma steht unter Komma.
• Wenn notwendig, Nullen ergänzen.
• Stellenweise berechnen, Überträge notieren.
0, 9
7
0
+
2 3, 4
0
0
+
5, 0
4
6
1 Schreibe stellengerecht untereinander
und berechne.
+ 2 9, 3
1
1
4 6, 5
1
1
0
–
1, 0
8
5
–
4, 7
0
0
1
1
1
8
8
5
d) 0,7653 – 0,275
0, 7 6 5 3
– 0, 2 7 5 0
1
1
7
7,
6
c) 0,932 + 0,76
0, 9 3 2
+ 0, 7 6 0
1
1, 6 9 2
4, 0 9
3, 6
1
1
2 9, 4
b) 21,91 – 17,82
2 1, 9 1
– 1 7, 8 2
13,67 – 1,085 – 4,7
0,97 + 23,4 + 5,046
1
a) 17,2 + 29,3
1 7, 2
Beispiel Subtraktion
Beispiel Addition
0, 4 9 0 3
e) 36,78 + 17,29 + 6,935
f) 0,073 + 0,107 + 2,377
g) 372,6 + 69,58 + 208,4
h) 78,96 – 12,23 – 23,61
3 7 2, 6 0 3 6, 7 8 0 0, 0 7 3
7 8, 9 6
+
6 9, 5 8
+ 1 7, 2 9 0
+ 0, 1 0 7
– 1 2, 2 3
+ 2 0 8, 4 0
+
6, 9 3 5
+ 2, 3 7 7
– 2 3, 6 1
2
2
2
1
6 3, 0 0 5
2
a)
2
1
6 5 0, 5 8
2, 5 5 7
4 3, 1 2
Welche Ziffern fehlen in den Berechnungen?
5 3 6, 2 9 + 2 7 1, 9 6
1
1
b)
1
7 0, 9 2 1 – 2 6, 8 7 3
1
8 0 8, 2 5
h
1
1
1
c)
0, 7 3 0 4 + 0, 6 1 9 7
1
1
1
1
1, 3 5 0 1
4 4, 0 4 8
d)
0, 5 4 6 9
– 0, 2 8 7 7
1
1
0, 2 5 9 2
3 Berechne den Rechnungsbetrag auf dem Kassenzettel.
Wie viel Euro muss der Kunde bezahlen, wie viel Geld bekommt er zurück?
4
Sarah hat einen Fahrradcomputer, der die gefahrenen Kilometer anzeigt.
a) Berechne die Länge der gefahrenen Strecken.
1. Strecke: Start:
2. Strecke:
3 9 8, 6
– 3 0 7, 9
=
9 0, 7 km
4 2 3, 1
– 3 9 8, 6
=
2 4, 5 km
43,17
6,83
b) Wie viel Kilometer muss Sarah noch fahren, bis der Computer 500 km anzeigt?
Rechnung: 500 km – 423,1 km = 76,9 km
Antwort:
Sie muss noch 76,9 km fahren.
11
Zunahmen und Abnahmen
z
Beispiel
Zunahmen lassen sich mit einem Plus-Zeichen
ausdrücken, Abnahmen mit einem Minus-Zeichen.
– 3 °C
+ 6 °C
+ 4 °C
– 11 °C
+ 3 °C (Zunahme)
– 7 °C (Abnahme)
1 Finde zu den Sätzen eine passende Aufgabe. Markiere die Wörter,
die dir Auskunft über die Rechnung geben. Überlege, ob es sich um eine Zunahme oder um eine Abnahme
handelt.
a) Morgens stand das Thermometer bei – 12 °C , bis
zum Mittag stieg die Temperatur um 8 °C . Wie viel
Grad hat es mittags?
b) Peter hat am Strand ein 50 cm tiefes Loch gegraben. Nun gräbt er noch 35 cm tiefer. Wie tief ist das
Loch jetzt?
+ 8 °C
– 35 cm
– 12 °C
– 4 °C
c) Sven hat 7 € Schulden und bekommt 20 € von
­seiner Tante. Wie viel Geld hat Sven jetzt?
– 50 cm
– 85 cm
d) In München ist es – 7 °C kalt, in Hamburg ist es
11 °C wärmer. Wie viel Grad hat es in Hamburg?
+ 20 €
+ 11 °C
– 7 €
13 €
e) Ein mit 80 km/h fahrendes Auto verringert seine
Geschwindigkeit um 30 km/h. Wie schnell fährt das
Auto?
– 7 °C
4 °C
f) Herr Engel fährt mit dem Aufzug vom
13. Stockwerk 8 Etagen nach unten. In welcher Etage
ist Herr Engel?
– 30 km/h
– 8 E
80 km/h
50 km/h
g) Thomas hat 50 Euro Schulden und leiht sich noch
einmal 30 Euro. Wie viel Euro Schulden hat Thomas?
– 30 €
– 50 €
13 E
h) Ein Bergsteiger steigt vom 8 400 m hohen Gipfel
2 500 m ab. Auf wie viel Meter ist der Bergsteiger
nun?
– 80 €
– 2 500 m
8 400 m
2
5 E
5 900 m
Die Karte zeigt die durchschnittlichen Tages– und Nachttemperaturen deutscher Städte.
Berechne den Temperatur–Unterschied für jede Stadt.
­
12
Stadt
Temperatur-Unterschied
Hamburg
8,3 °C
Rostock
9,6 °C
Berlin
9,6 °C
Leipzig
7,9 °C
Köln
11 °C
Frankfurt
9,2 °C
Stuttgart
10,2 °C
München
9,3 °C
Textaufgaben lesen und verstehen
Schritte beim Lösen von Textaufgaben:
Beispiel
1. Die Aufgabe genau durchlesen.
2. Markieren: Was ist gegeben?
3. Markieren: Was ist gesucht?
4. Rechenweg suchen und berechnen.
5. Antwortsatz formulieren.
Für eine Theaterveranstaltung wurden 1 187 Karten
verkauft . Das Theater hat insgesamt 1 312 Plätze .
Wie viele Plätze waren noch frei?
1. Lesen
2. Gegebenes markieren (hier orange).
3. Gesuchtes markieren (hier grau).
4. Rechenweg: 1 312 – 1 187 = 125
5. Antwortsatz: Im Theater waren noch 125 Plätze frei.
1 Miriam hat einen Nebenjob: Sie trägt an 5 Tagen in der Woche Zeitungen aus. Pro Zeitung bekommt
sie 15 Cent. Insgesamt muss sie jeden Tag 84 Zeitungen verteilen. Wie viel verdient sie in 4 Wochen?
a) Gegebene Größen sind:
Verdienst pro Zeitung:
15 Cent
Anzahl der Zeitungen:
84
Anzahl der Arbeitstage pro Woche:
5
Anzahl der Wochen im Monat:
4
b) Schreibe zu jedem Rechenschritt auf, was Miriam berechnet.
1
84 ∙ 0,15 € = 12,60 €
2
4 ∙ 5 = 20
3
20 ∙ 12,60 € = 252,00 €
1
84 Zeitungen mal 15 Cent macht 12,60 € pro Tag.
2
4 Wochen mal 5 Arbeitstage = insgesamt 20 Arbeitstage.
3
20 Tage mal 12,60 € = 252,00 € Verdienst pro Monat.
c) Schreibe nun einen passenden Lösungssatz auf.
Miriam verdient 252,00 € im Monat.
2 Lies den Artikel über das Wunder von Lengede durch
und beantworte die Fragen zum Text:
a) Am wievielten Tag konnten die letzten eingeschlossenen
Männer gerettet werden?
Am 15. Tag konnten die letzten Männer gerettet werden.
b) Für wie viele Männer kam die Rettung zu spät?
Für 35 Personen kam die Hilfe zu spät.
(Rechnung: 128 – 79 – 3 – 11 = 35)
c) Wie viele Tage waren die drei Bergleute, die am ersten
November gerettet wurden, eingeschlossen?
Sie waren 8 Tage eingeschlossen.
e
Das Wunder von Lenged
ch der Klärteich 12
Am 24. Oktober 1963 bra
e-Broistedt ein.
der Eisenerzgrube Lenged
Kubikmeter
Rund eine halbe Million
die Grube ein
in
Schlammwasser drang
(das sind die
llen
Sto
die
und überflutete
Bergleute und
Gänge im Bergwerk). 128
sich zu jener Zeit
ein Monteur befanden
Stunden nach
ten
unter Tage. In den ers
79 von ihnen in
h
sic
n
nte
dem Unglück kon
die übrigen schien
Sicherheit bringen. Für
zu geben. Drei
es keine Hoffnung mehr
November nach
1.
Bergleute konnten am
tion geborgen
hak
Suc
einer fieberhaften
e später gelang
werden. Weitere zwei Tag
Kontakt mit weies den Bergungsteams,
n aufzunehmen.
ene
teren elf Eingeschloss
Tage und 22
hn
rze
vie
,
Am 7. November
ck, wurden sie
Stunden nach dem Unglü
gerettet.
13
Textaufgaben
1 Thomas fährt mit dem Auto in den Urlaub. Der Kilometerzähler zeigt zu
Beginn 36 948 km an, bei der Rückkehr 41 109 km. Wie viel Kilometer hat er
zurückgelegt?
Raum für Nebenrechnungen:
Rechnung: 41 109 km – 36 948 km = 4 161 km
Antwort:
Er hat 4 161 km zurückgelegt.
2
Ein Parkhaus hat 1 875 Plätze. Im Laufe des
Vormittags fuhren 1 739 Autos hinein und 617 heraus.
Wie viele Plätze sind zurzeit noch frei?
Trage die Lösung in die Anzeigentafel ein.
P
Parkhaus
Freie Plätze:
7
5
3
Rechnung: 1 875 – 1 739 + 617 = 753
Antwort:
Zurzeit sind noch 753 Plätze frei.
3
Für das Fußballspiel München - Hamburg wurden 41 142
Sitzplatzkarten und 18 448 Stehplatzkarten verkauft. Das Stadion fasst 69 000 Zuschauer. Wie viele Plätze waren noch frei?
Rechnung: 69 000 - (41 142 + 18 448) = 69 000 – 59 590 = 9 410
Antwort:
Es waren noch 9 410 Plätze frei.
4 Der Mount Everest ist mit 8 848 Metern der höchste Berg der Erde.
Der Montblanc mit 4 807 Metern der höchste Berg in Europa.
a) Wie groß ist der Höhenunterschied der beiden Berge?
Rechnung: 8848 – 4807 = 4041
Antwort:
Der Höhenunterschied beträgt 4 041 m.
b) Die Zugspitze ist 2 963 m hoch. Berechne den Höhenunterschied
– zum Mount Everest:
5 885 m
– zum Montblanc:
1 844 m
5
Cems Girokonto hat einen Kontostand von 238,40 €.
a) Zum Geburtstag bekommt Cem von seiner Tante 50 € überwiesen. Von seinem
Geld kauft er sich einen DVD-Player für 79,95 €. Wie viel Geld ist nun auf seinem
Konto? Fülle Cems Kontoauszug aus.
b) Cem hat sein Motorrad in die Werkstatt gebracht. Da einige Teile ausgetauscht
werden müssen, wird die Reparatur 250 € kosten. Kann Cem die
Reparatur bezahlen, ohne sein Konto zu überziehen?
Sparbank
Antwort: ja
nein
alter Kontostand:
+ 50,00 €
Überweisung
Lastschrift DVD-Player
neuer Kontostand:
14
238,40 €
– 79,95 €
208,45 €
Test: Grundrechenarten 1
1
Auf welche Zahlen zeigen die Pfeile?
150
300
50
0 100
60 489 + 40 614
2 6 4 5
+ 6 2 3 2
8 8 7 7

8 749 – 2 635
1
9 6 0 8 0 7
+ 6 3 4 4 1 9 3
1
1
1 0 1 1 0 3

40 382 – 29 691
6 1 1 4
1 0 6 9 1
1

53,21 + 31,4 + 14,53
1
1
1

1
1
1
1
2
1
1
7 3 0 5 0 0 0

1
1

1
9 6 0 9 0 9

3 849,073 – 184,652 – 2 364,416
6 3, 4 2 1
+
8, 7 9 4
+ 2 7 3, 6 8 7
9 9, 1 4
1
2 0 0 9 8 2 4
– 1 0 4 8 9 1 5
63,421 + 8,794 + 273,687
5 3, 2 1
+ 3 1, 4 0
+ 1 4, 5 3
1
2 009 824 – 1 048 915
4 0 3 8 2
– 2 9 6 9 1
3

960 807 + 6 344 193
8 7 4 9
– 2 6 3 5
0
6 0 4 8 9
+ 4 0 6 1 4
1
– 100

125
Berechne schriftlich.
2 645 + 6 232
– 200
100 200

2
225
3 8 4 9, 0 7 3
–
1 8 4, 6 5 2
– 2 3 6 4, 4 1 6
1
1
3 4 5, 9 0 2

1
1
1 3 0 0, 0 0 5

Berechne die Temperaturdifferenz.
7 : 00 Uhr: + 2 °C
Differenz:
7 : 00 Uhr: – 2 °C
Differenz:
13 °C
12 : 00 Uhr: + 8 °C
10 °C
12 : 00 Uhr: + 15 °C

7 : 00 Uhr: – 5,4 °C
12 : 00 Uhr: + 12,8 °C

Differenz:
18,2 °C

4 Johanna kauft sich neue
Möbel für ihr Zimmer: Ein Bett für
398 €, einen Schreibtisch für
275 € und einen Schrank für
199 €. Wie viel muss sie insgesamt bezahlen?
Herr Reiche kauft ein neues Auto
für 28 950 € und gibt sein altes
Auto für 12 500 € in Zahlung. Wie
viel Euro muss Herr Reiche
zuzahlen?
Frau Lange verdient monatlich
1 876 €. Davon werden für Steuern
317,85 € und für Versicherungen
196,15 € abgezogen. Was
bekommt sie überwiesen?
398 € + 275 € + 199 €
= 872 €

28 950 € – 12 500 €
= 16 450
1 876 € – 317,85 € – 196,15 €
= 1 362 €
Bronze:
Gold:
Silber:


(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 77.)
15
Kopfrechnen: Multiplizieren und dividieren
Multiplizieren (malnehmen)
Dividieren (teilen)
Faktor mal Faktor = Produkt
124234445 14345 124234445 12222344245
12
∙
6 = 72
Dividend geteilt durch Divisor = Quotient
12224423444445 12222222322222245 1224234245 12222344445
72
:
6 = 12
1
a) 7 ∙ 9 =
63 8 ∙ 6 =
48 11 ∙ 11 =
121 49 : 7 =
5 ∙ 4 =
20 17 ∙ 10 =
170 48 : 12 =
2
h
Berechne im Kopf.
b) 4 ∙ 12 =
48 c) 30 : 5 =
6
7
39 :
5
4
d) 9 ∙ 8
= 72
3
= 13
∙ 15 = 75
Fülle die Tabellen aus.
Die Zahl
35
75
90
125
350
200
600
Das Doppelte
70
150
180
250
700
400
1 200
Die Zahl
60
90
104
260
340
160
840
Die Hälfte
30
45
52
130
170
80
420
Die Zahl
25
70
95
120
25
40
80
Das Dreifache
75
210
285
360
75
120
240
3 Zahlenketten: Setze als Startzahl nacheinander die Zahlen aus der Tabelle ein und notiere das Ergebnis
in der Tabelle.
Startzahl
h
· 2
· 5
· 10
: 2
Startzahl
5
10
15
20
50
2
40
Zielzahl
50
100
150
200
500
20
400
4
Fülle die Zahlenmauern aus. Achtung, hier wird von unten nach oben multipliziert.
10 000
4 000
40
100
10
10
2
16
Zielzahl
: 5
5
4
2
250
40
10
4
2
2
2
25
5
5
Schriftliches Multiplizieren (·)
Beispiel: 4902 · 35
4
1. Schritt: Stellenweise malnehmen.
2. Schritt: Die Zwischenrechnungen addieren.
3. Schritt: Das Ergebnis doppelt unterstreichen.
9
0
2
∙
3
1
4
7
0
6
2
4
5
1
0
1
5
7
0
1
1
Mit dem Überschlag kannst du das Ergebnis kontrollieren.
1
b) 7 9 ∙ 1 2 5 7 9
1 5 8
3 9 5
1
1
2 2 0 8
Ü: 5 000 ∙ 40 = 200 000
Ergebnis kann stimmen.
1
c) 6 8 ∙ 1 2 3 6 8
1 3 6
2 0 4
1
d) 1 2 ∙ 7 8 9
8 4
9 6
1 0 8
1
9 8 7 5
1
8 3 6 4
9 4 6 8
Berechne und kontrolliere mit einer Überschlagsrechnung.
a) 397 ∙ 6
b) 708 ∙ 7
c) 904 ∙ 5
d) 870 ∙ 8
3 9 7 ∙ 6
2 3 8 2
7 0 8 ∙ 7
4 9 5 6
9 0 4 ∙ 5
4 5 2 0
8 7 0 ∙ 8
6 9 6 0
Ü: 400 ∙ 6 = 2 400
Ü: 700 ∙ 7 = 4 900
Ü: 900 ∙ 5 = 4 500
Ü: 900 ∙ 8 = 7 200
e) 4 329 ∙ 24
f) 6 153 ∙ 72
4 3 2 9 ∙ 2 4
8 6 5 8
1 7 3 1 6
g) 4 137 ∙ 32
6 1 5 3 ∙ 7 2
4 3 0 7 1
1 2 3 0 6
1
h) 7 138 ∙ 484
Ü: 6 000 ∙ 70 = 420 000
i) 4 847 ∙ 702
7 1 3 8
2 8 5
5 7
2
1
4 4 3 0 1 6
Ü: 4 000 ∙ 25 = 100 000
4 8 4 7 ∙ 7 0 2
3 3 9 2 9
0 0 0 0 0
9 6 9 4
3 4 5 4 7 9 2
3 4 0 2 5 9 4
1
∙
5
1
8
1
1
Ü: 7 000 ∙ 500 = 3 500 000
1 3 2 3 8 4
Ü: 4 000 ∙ 30 = 120 000
j) 3 076 ∙ 816
4 8 4
2
0 4
5 5 2
1
4 1 3 7 ∙ 3 2
1 2 4 1 1
8 2 7 4
1
1 0 3 8 9 6
h
7
Was gehört in die Felder?
a) 9 2 ∙ 2 4 1 8 4
3 6 8
2
5
1
3 0 7 6
2 4 6
3
1
1
Ü: 5 000 ∙ 700 = 3 500 000
1
1
∙
0
0
8
2
8 1 6
8
7 6
4 5 6
1
2 5 1 0 0 1 6
Ü: 3 000 ∙ 800 = 2 400 000
3 Ein Mountain-Bike wird zum Barpreis von 624 € angeboten. In einem anderen Geschäft bekommt man
das gleiche Fahrrad für 12 Monatsraten zu je 56 €.
5 6 ∙ 1 2
Welches Angebot ist günstiger?
Barpreis: 624 €
Ratenpreis: 672 €
günstiger: Barpreis
5 6
1 1 2
6 7 2
17
Schriftliches Dividieren (:)
Beispiel: 2 142 : 7
2
2
1. Schritt: Stellenweise teilen (links beginnen).
2. Schritt: Ergebnis doppelt unterstreichen.
1
4
2
1
0
4
:
7
:
7
:
7
:
7
=
3
0
6
Ü: 2 100 : 7 = 300
Ergebnis kann
stimmen.
0
Mit dem Überschlag kontrollieren.
4
2
4
2
0
1
Was gehört in die Felder?
a) 392 : 7
b) 979 : 11
3 9 2 : 7 = 5 6
3 5
4 2
4 2
0
Ü: 350 : 7 = 50
2
9 7 9 :
8 8
9 9
9 9
0
1 2 = 6 5 7
Ü: 7 200 : 12 = 600
b) 52 192 : 8 = 6 524
c) 15 696 : 24 = 654
Ü: 56 000 : 8 = 7000
Ü: 15 000 : 25 = 600
Berechne die Aufgaben auf einem Extrablatt. Die Lösungen findest du auf den orangen Kärtchen.
a) 5 940 : 12 =
495
3 254
3 258
e) 6 764 : 89 =
b) 117 144 : 36 = 3 254
75
76
18
7 8 8 4 :
7 2
6 8
6 0
8 4
8 4
0
Berechne die Aufgaben. Denke an den Überschlag.
Ü: 2 800 : 7 = 400
3
1 1 = 8 9
Ü: 990 : 11 = 90
a) 2 555 : 7 = 365
h
c) 7 884 : 12
76
495
c) 59 964 : 76 =
f) 17 145 : 5 = 3 429
d) 8 768 : 137 =
30
3429
3 424
789
789
g) 14 656 : 458 =
54
32
799
49
32
64
64
h) 2 793 : 57 =
49
Verbindung der vier Grundrechenarten
Klammer zuerst
Punkt-vor-Strich
Was in der Klammer steht, wird zuerst berechnet. Zuerst Punktrechnung (∙/:),
dann Strichrechnung (+/–).
Beispiel
Beispiel
Klammerrechnung:
5 ∙ (10 – 7)
= 5 ∙
1
1443445
3
144434445
= 15
= 70
= 100 – 60 = 40
= 81 : 3 = 27
1443445
= 49 + 3
= 52
= 84 : 7 = 12
m)50 – (20 – 5 ∙ 4)
= 50 – 0 = 50
= 54 – 24 = 30
= 40 : 4 – 8 = 2
= 80 : 10 = 8
= 11 ∙ 8 = 88
=5–5=0
= 72 : 3 = 24
= 20 ∙ 25 = 500
= 12 ∙ 5 = 60
l) 24 + 3 ∙ 4 – 10
o) (12 ∙ 6) : 3
h) (48 : 4) ∙ 5
k) 25 : 5 – 5
n) (60 – 20) : 4 – 8
d) (24 – 4) ∙ 25
g) 11 ∙ (17 – 9)
j) 54 – 8 ∙ 3
= 28 + 6 = 34
2
= 43
c) 80 : (2 + 8)
f) (28 + 56) : 7
i) 28 + 42 : 7
= 50 – 7
b) (72 + 9) : 3
e) 100 – (80 – 20)
1443445
: 7 = 10
Berechne.
a) 8 ∙ (6 + 9)
1443445
= 8 ∙ 15 = 120
Punkt-vor-Strichrechnung:
5 ∙ 10 – 7
49 + 21 : 7
(49 + 21) : 7
= 24 + 12 – 10 = 26
p) 12 ∙ (60 : 6)
= 12 ∙ 10 = 120
Berechne.
a) 17 + 8 ∙ 3
= 17 + 24 = 41
(17 + 8) ∙ 3 = 25 · 3 = 75
8 ∙ 3 + 17
b) 50 + 12 : 2 = 50 + 6 = 56
(50 + 12) : 2 = 62 : 2 = 31
= 24 + 17 = 41
12 : 2 + 50 = 6 + 50 = 56
8 ∙ (3 + 17) = 8 · 20 = 160
12 : (2 + 50) = 12 : 52 ≈ 0,23
c) Vergleiche die Lösungen.
Welche Lösung ist bei a) die kleinste Lösung? 41 Welche Lösung bei b)? 0,23
Welche Lösung ist bei a) die größte? 160 Welche bei b)? 56
Was haben alle Aufgaben bei a) und b) jeweils gemeinsam?
Sie bestehen aus den gleichen Zahlen.
19
Textaufgaben
1 Ein Sportverein hat als Mitglieder 782 Jugend-
liche und 1 205 Erwachsene. Wie viel Euro nimmt der Verein im Monat an Beiträgen ein?
Monatsbeitrag:
Jugendliche
6 €
Erwachsene
12 €
Rechnung: 782 · 6 + 1 205 · 12 = 4 692 + 14 460 = 19 152 €
Antwort:
Der Verein nimmt im Monat 19 152 € ein.
2 In einem Automobilwerk werden 736 Autos eines Typs auf Waggons verladen. Auf einen Waggon passen 8 Autos. Wie viele Waggons muss der Güterzug
haben, damit alle Autos verladen werden können?
Rechnung: 736 : 8 = 92
Antwort:
Der Güterzug hat 92 Waggons.
3 Vor einer Fähre stehen 294 Autos im Stau. Bei jeder Fahrt – ungefähr alle
10 Minuten – kann eine Fähre 42 Autos übersetzen.
a) Wie häufig muss die Fähre fahren, um alle wartenden Autos überzusetzen?
Rechnung: 294 : 42 = 7
Antwort:
Die Fähre muss 7-mal fahren.
b) Wie lange muss das letzte Auto der wartenden Schlange noch auf die Überfahrt warten? Rechnung: 6 · 10 Minuten = 60 Minuten
Antwort:
Das letzte Auto muss 60 Minuten (1 Stunde) warten.
4 Silvio kauft einen Kasten Mineralwasser. Jede der 12 Flaschen kostet 0,40 € zuzüglich 0,15 € Pfand. Für den Kasten muss er 1,50 € Pfand bezahlen.
a) Was kostet der Kasten Mineralwasser insgesamt?
12 ∙ (0,4 + 0,15) + 1,5 = 8,10 €
Wasser:
8,10 €
b) Schreibe die gesamte Rechnung in einem einzigen Rechenausdruck (mit Klammern).
12 ∙ (0,4 + 0,15) + 1,5 = 8,10 €
5 a) Wie viel spart man pro Schwimmbadbesuch wenn man eine Zehnerkarte kauft?
Schwimmbad
Eintrittspreise:
Tageskarte
1,40 €
10er-Karte
10,00 €
Rechnung: 10 ∙ 1,40 € = 14,00 € 4 € : 10 = 0,40 €
Antwort:
Man spart 0,40 €.
b) Wie oft muss man mindestens ins Schwimmbad gehen, damit sich eine Zehnerkarte lohnt?
Man muss 8 -mal ins Schwimmbad gehen.
20
Raum für Nebenrechnungen
Test: Grundrechenarten 2
1
Berechne im Kopf.
200 – 50 : 5 = 190
2

27 + 3 ∙ 10 – 5 = 52


70 + (30 – 7 ∙ 4) = 72
Berechne schriftlich.
4 125 ∙ 7
6 808 ∙ 74
4 1 2 5 ∙ 7
2 8 8 7 5
70 193 ∙ 806
6 8 0 8 ∙ 7 4
4 7 6 5 6
2 7 2 3 2
1
7 0 1 9
5 6 1
0 0
4
5 6 5
1
5 0 3 7 9 2

948 : 4

1 330 : 7
9 4 8 : 4 = 2 3 7
8
1 4
1 2
2 8
2 8
0

5 ∙ 3 147 m = 15 735 m
Die Strecke ist 15 735 Meter lang.

546 Seiten : 7 Tage = 78
Pia muss pro Tag 78 Seiten lesen.

Gold:
0 6
0
5 8
5 8

9
7
1
1
Pia möchte ein Buch mit 546 Seiten in einer Woche durchlesen.
Wie viele Seiten muss sie täglich
lesen?
Silber:
8
4
0
1
5
9 555 : 39
3 Bei einem Radrennen ist
ein Rundkurs von 3 147 m fünfmal
zu durchfahren. Wie lang ist die
Gesamtstrecke?
Bronze:
∙
4
0
1
5
1 3 3 0 : 7 = 1 9 0
7
6 3
6 3
0 0
0 0
0

3
5
0
2
7
5
8
7
5
1
1
5 5 : 3 9 = 2 4 5
5
6
9 5
9 5
0

Ein Handy kostet bei Barzahlung
340 €. Man kann das Handy aber
auch ein Jahr lang mit einer
monatlichen Rate von 30 €
bezahlen. Um wie viel Euro ist
der Barpreis günstiger?
12 ∙ 30 € = 360 €
360 – 340 = 20
Der Barpreis ist 20 € günstiger.

(Richtig gelöste Aufgaben ankreuzen. Die Lösungen findest du auf Seite 77.)
21
Längen umrechnen
1. Schritt:Grundbeziehungbestimmen:
VonwelcherGrößewirdin
welcheGrößeumgerechnet?
(Pfeilrichtungbeachten!)
2. Schritt:Umrechnungbestimmen.
3. Schritt:Berechnen.
Beispiel: 2 600 cm in m
4. Schritt:Notieren.
Maßzahl
1Millimeter(mm)
10Millimeter(mm)=1Zentimeter(cm)
10Zentimeter(cm)=1Dezimeter(dm)
10Dezimeter(dm) =1Meter(m)
1000Meter(m)
=1Kilometer(km)
gemessen
HöheeinerTür
Durchmessereiner
1-€-Münze
Längedieses
Arbeitsheftes
cm
∙10
dm
∙10
m
in
∙10
∙
dm =
a) 8m
=
80
dm
b) 7000m
=
7
km
c) 3dm
=
30
cm
d)80mm
=
8
cm
e) 9km
=
9 000
m
f)40cm
=
4
dm
Höhedes
Schultisches
g) 22m
=
2 200
cm
Breitedieses
Arbeitsheftes
h) 40m
=
40 000
mm
Längedes
Klassenzimmers
i) 4km
=
40 000
dm
2,2
km
3
BerechnewieimBeispiel.
Beispiel: 15,2 km + 2 960 m = 15 200 m + 2 960 m = 18 160 m = 18,16 km
a) 16,3m+780cm
= 1 630 cm + 780 cm = 2 410 cm = 24,1 m
b) 3,2km+560m
= 3 200 m + 560 m = 3 760 m = 3,76 km
c) 616cm+2,54m
= 616 cm + 254 cm = 870 cm = 8,7 m
d) 3,5m–28dm
= 35 dm – 28 dm = 7 dm = 0,7 m
e) 6,5m–385cm
= 650 cm – 385 cm = 265 cm = 2,65 m
:1000
km
∙1000
RechneindieangegebeneEinheitum.
j) 220000cm =
f) 3,5dm+295mm = 350 mm + 295 mm = 645 mm = 6,45 dm
22
=:
10
:10
10
mm
= : 1 0 : 10
0
SchätzediefolgendenGrößen.
Missdannnach.
geschätzt
:10
2
1
in m
cm
:10
m
1. mindm:
2.Umrechnung=∙10
3.12∙10=120
4.12m=120dm
Maßeinheit
Grundbeziehungen bei Längen:
1. cminm:
2.Umrechnung=:100
3. 2600:100=26
4. 2600cm=26m
Beispiel: 12 m in dm
7m
EineGrößebestehtaus
MaßzahlundMaßeinheit.
Achtung!Längenkannmannur
zusammenrechnen,wennsieinde
r
gleichenEinheitangegebensind!
Flächen umrechnen
Erinnerung
1. Grundbeziehungbestimmen.
2. Umrechnungbestimmen.
3. Berechnen.
4. Notieren.
Grundbeziehungen bei Flächen:
1Quadratmillimeter(mm2 )
=1Quadratzentimeter(cm2 )
=1Quadratdezimeter(dm2 )
=1Quadratmeter(m2 )
=1Ar(a)
=1Hektar(ha)
=1Quadratkilometer(km2 )
2
100Quadratmillimeter(mm )
100Quadratzentimeter(cm2 )
100Quadratdezimeter(dm2 )
100Quadratmeter(m2 ) 100Ar(a)
100Hektar(ha)
Beispiel: 5 800 m2 in a
:100
:100
in
a = : 10
0
:100
Beispiel: 13 m2 in cm2
m
2
1.m2 ina:
2.Umrechnung=:100
3.5800:100=58
4.5800m2 =58a
:100
:100
:100
2
∙100
dm2
∙100
m2 ∙100
2
1
2
= ∙ 1 ∙ 100
00
b) 37dm2 = 3 700 cm2
d) 682cm2 = 68 200 mm2
e) 173m2 g) 7033ha = 703 300 a
h) 1,5m2 = 3 800 ha
∙100
∙100
=
= 5 800 a
c) 58ha
= 17 300 dm2
f) 124km2 = 12 400 ha
= 150 dm2
i) 0,75cm2 = 75 mm2
RechneindienächstgrößereEinheitum.
a) 2300cm2 = 23 dm2
d) 5900a
= 59 ha
g) 8000ha = 80 km2
3
∙100
km2
ha
RechneindienächstkleinereEinheitum.
a) 38km2
2
a
∙1
in
cm
00
cm2 00
mm2 m
1.m2 incm :
2.Umrechnung=∙10000
3.13∙10000=130000
4. 13m2=130000cm2
b) 6900mm2= 69 cm2
c) 500dm2 = 5 m2
e) 1200dm2 = 12 m2
f) 1500m2 = 15 a
h) 750dm2
= 7,5 m2
i) 90mm2 = 0,9 cm2
RechneindieangegebeneEinheitum.
a) 8m2
= 80 000
cm2
b) 2600ha= 26
d) 5600m2 = 56
a
e) 129a
g) 67ha
= 6 700
a
h) 300cm2 = 3
j) 591000m2 = 5 910
a
k) 575ha
= 5,75
dm2
n) 2km2
= 20 000 a
m)740000mm2 = 74
= 12 900
km2
c) 7cm2
m2
f) 9700a = 97
dm2 i) 238km2 = 23 800 ha
km2
l) 6,25cm = 625
= 700
2
mm2
ha
mm2
2
o) 42,5dm = 425 000 mm2
23
Gewichte umrechnen
1. mging:
2.Umrechnung=:1000
3.15000:1000=15
4.15000mg=15g
Grundbeziehungen bei Gewichten:
1Milligramm(mg)
1000Milligramm(mg) =1Gramm(g)
1000Gramm(g)
=1Kilogramm(kg)
1000Kilogramm(kg) =1Tonne(t)
Beispiel: 34 t in kg
1. tinkg:
2.Umrechnung=∙1000
3. 34∙1000=34000
4. 34t=34000kg
m
gi
n g = : 1 000
:1000
mg
:1000
g
:1000
kg
∙1000
t
∙1000
∙1000
t
in
1 SchätzedasGewichtderfolgendenGegenstände.Wiegedann.
geschätzt
gemessen
2
0
0
Beispiel: 15 000 mg in g
kg = ∙ 1 0
RechneindieangegebeneEinheitum.
a) 18t = 18 000 kg
b) 8000g =
8
kg
c) 7kg = 7 000 g
d) 3000mg=
3
g
f) 9000kg =
9
t
10
kg
MeinMäppchen
e) 6g
2-€-Münze
g) 30kg= 30 000 g
h) 10000g =
DiesesArbeitsheft
i) 3,4t = 3 400 kg
j) 67,5kg = 67 500 g
MeineSchultasche
k) 0,5t = 500 kg
l) 500g
3
4
RechneindienächstkleinereEinheitum.
= 6 000 mg
= 0,5 kg
RechneindienächstgrößereEinheitum.
a) 3kg = 3 000 g
b) 62g = 62 000 mg
a) 5000g = 5 kg
c) 12000kg = 12 t
c) 25t = 25 000 kg
d) 14kg = 14 000 g
b) 4200mg= 4,2 g
d) 124000g = 124 kg
e) 1,5t = 1 500 kg
f) 2,5kg = 2 500 g
e) 4500kg = 4,5 t
h) 28000mg= 28 g
g) 0,5g= 500 mg
h) 1,4kg = 1 400 g
g) 4650g = 4,65 kg 5
BerechnewieimBeispiel.
Beispiel: 2,3 kg + 800 g = 2 300 g + 800 g = 3 100 g = 3,1 kg
a) 9,8kg+749g
= 9 800 g + 749 g = 10 549 g = 10,549 kg
b) 6,43t+880kg
= 6 430 kg + 880 kg = 7 310 kg = 7,31 t
c) 20,92g+164mg = 20 920 mg + 164 mg = 21 084 mg = 21,084 g
d) 55,125kg–625g = 55 125 g – 625 g = 54 500 g = 54,5 kg
e) 5,94g–385mg = 5 940 mg – 385 mg = 5 555 mg = 5,555 g
24
f) 500g
= 0,5 kg
Zeitpunkte und Zeitspannen
Grundbeziehungen beim Rechnen
mit Zeit
1 Tag (d)
= 24 Stunden (h)
1 Stunde (h) = 60 Minuten (min)
1 Minute (min) = 60 Sekunden (s)
: 60
: 60
s
min
· 60
d
· 24
1. s in min:
2. Umrechnung = : 60
3. 240 : 60 = 4
4. 240 min = 4 h
3 Für eine Fahrt von Stuttgart nach Berlin gibt
es die folgenden Verbindungen:
Rechne in die angegebene Einheit um.
a) 4 min =
240
s
b) 72 h
=
3
d
c) 3 h
=
180
min
d) 480 min =
8
h
e) 5 d
=
120
h
f) 540 s
=
9
min
min
h) 7 d
=
168
g) 300 s =
2
1. h in min:
2. Umrechnung = · 60
3. 3 · 60 = 180
4. 3 h = 180 min
5
h
Ergänze die Tabelle.
Abfahrt
11:35 Uhr
22:47 Uhr
Fahrtdauer
2 Stunden
12 Minuten
1 Stunde
7 Minuten
Ankunft
13:47 Uhr
23:54 Uhr
7:55 Uhr
4 h 17 min
12:12 Uhr
22:44 Uhr
1,5 Stunden
0:14 Uhr
3:05 Uhr
1 Stunde
5 Minuten
7h 30 min
9
Verbindung 1: 5 Stunden 26 Minuten
Verbindung 2: 5 Stunden 58 Minuten
Verbindung 3: 5 Stunden 26 Minuten
Verbindung 4: 5 Stunden 35 Minuten
12
2:55 Uhr
a) Wie lange dauern die Fahrten? Markiere die
schnellste Verbindung.
3
6
10:35 Uhr
Thema: Zeitzonen
Die Karte zeigt die Zeitzonen der Erde. Jeder Ort
innerhalb einer Zeitzone hat dieselbe Uhrzeit. Bei
uns in Mitteleuropa gilt die Mitteleuropäische Zeit
(MEZ).
Erkläre, warum Vorzeichen bei den Zeitangaben verwendet werden.
1
2 Gib drei europäische Städte an, die außerhalb
der MEZ-Zone liegen. Wie viel Zeitunterschied
herrscht jeweils?
3 Wann würde man von Deutschland aus in den
USA anrufen, ohne jemanden nachts zu wecken?
b) Frau Reiser will frühestens um 12:00 Uhr in Stuttgart abfahren und spätestens um 18:30 Uhr in Berlin
sein. Welche Verbindungen kann sie auswählen?
Verbindungen 2 und 3
Anchorage
Nuuk
London
Denver
New York
San
Francisco
MexicoCity
Kairo
Dakar
Yakutsk
Helsinki
Moskau
Berlin
Peking
Neu Delhi Tokio
Bangkok
Lagos
Mombasa
Lima
Rio de
Janeiro
Kapstadt
Datumsgrenze
1
Beispiel: 240 s in min
: 24
h
· 60
Beispiel: 3 h in min
Perth Sydney
–12 –11 –10 –9 –8 –7 –6 –5 –4 –3 –2 –1 MEZ +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12
25
Test: Größen
1
Rechne in die angegebene Einheit um.
4 min
=
6 m
=
4 kg
=
240
600
4 000
2 500 d​m2​ ​ =
2
25
s
2 d
=

7 km
=

=

12,5 ​m2​ ​

4 000 mm=
cm
g
m
7 000
1250
40
2,5 kg =
2 500

90 min=
1,5


2 k​m2​ ​ = 20 000 a

2 ​ _4 ​ h =
h
m
d​m2​ ​
1
dm
g

h

135

min

Berechne.
12 km + 980 m =
8,54 kg – 763 g =
5 min 12 s – 127 s =
12 000 m + 980 m
8 540 g – 763 g
312 s – 127 s
= 12 980 m
= 7 777 g
= 185 s
= 12,98 km

= 7,777 kg

= 3 min 5 s
5,25 kg – 790 g =
0,5 min + 45 s =
12 m – 74 mm =
5 250 g – 790 g
30 s + 45 s
12 000 mm – 74 mm
= 4 460 g
= 75 s
= 11 926 mm
= 4,46 kg
= 1 min 15 s
= 1,1926 m

3 Ein Flugzeug startet um
8:39 Uhr. Die Flugzeit beträgt 2 h
24 min. Wann landet das
Flugzeug?
Ein Flugzeug startet um 8:39 Uhr.
Es landet um 13:24 Uhr. Wie lange
war es in der Luft?
Bronze:



Welche Zugverbindung ist
schneller?
ab Hamburg
an Hannover
1
12:01
13:23
2
13:24
14:49
4 h 45 min
11:03 Uhr
26
48

Silber:
Gold:

Verbindung 1: 1 h 22 min
Verbindung 2: 1 h 25 min
Die erste Verbindung ist
schneller.
(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 77.)

Bruchteile bestimmen
Beispiel
1. Schritt: Nenner bestimmen:
In wie viele gleich große
Teile ist das Ganze zerlegt?
2. Schritt: Zähler bestimmen:
Wie viele der gleich großen
Teile bilden den Anteil?
3. Schritt: Bruch notieren.
1
1. Der Kreis ist in 5 gleich große Teile
zerlegt. Der Nenner ist 5.
2. Die Anzahl der gefärbten Teile ist 4.
Der Zähler ist 4.
3. Der Bruch heißt: _45
Zähler
Bruchstrich
Nenner
4
_
5
Ergänze die Sätze.
a) Die Pizza ist in
5
gleich große Stücke zerlegt.
c) 3 Stücke sind
1
___
b) Jedes Stück der Pizza ist 5
der Pizza.
3
___ der Pizza.
5
2
d) Färbe _5 der Pizza ein.
2
Schreibe als Bruch, welche Anteile hier markiert worden sind.
1
____
4
1
____
8
3
4
____
6
3
____
8
3
____
6
3
____
8
8
____
12
4
____
10
8
____
16
2
____
6
2
____
8
2
____
9
6
____
8
2
____
10
Färbe beim Rechteck den angegebenen Bruchteil.
a) _45
4
3
____
6
1
b) __
10
7
c) __
20
Durch Falten eines Blattes kannst du Brüche darstellen.
a) Falte ein Blatt Papier so zusammen und wieder auseinander, dass du zwei
gleich große Teile erhältst. Beschrifte die Bruchteile des Blattes.
1
b) Nimm jedes Mal ein neues Blatt Papier und stelle die Brüche _41 , _81 und __
16 dar.
Beschrifte auch hier die Bruchteile auf dem Blatt.
1
c) Versuche den Bruch _3 darzustellen.
27
Brüche und gemischte Zahlen
1
Ist bei einem Bruch der Zähler größer
als der Nenner, kann er in eine
gemischte Zahl umgewandelt werden.
Welche gemischte Zahl ist dargestellt?
a)
17
Beispiel: __
​ 3  ​
Umwandlung Bruch
Zahl
1. Schritt: Zähler durch den Nenner
teilen, Rest bestimmen.
2. Schritt: Ergebnis als gemischte Zahl
notieren.
17
1.​ __
3  ​= 17 : 3
= 5 Rest 2
17
2
14
1. 2 = 2 · ​ _7 ​= __
​ 7  ​
15
1
_ __
2.​ __
7  ​+ ​ 7 ​= ​ 7  ​
1
5 3
_
​ 5 ​+ _​ 5 ​
=
1 + _​ 5 ​= 1 ​ _5 ​
4 3
_
​ 4 ​+ _​ 4 ​
=
1 + _​ 4 ​= 1 ​ _4 ​
2
2
3
3
3
3
1
14
1 + _​ 3 ​= 1 ​ _3 ​
b)
Beispiel: 2 _​ 7 ​
7
=
2
_
_
2.​ __
3  ​= 5 + ​ 3 ​= 5 ​ 3 ​
Umwandlung Zahl
Bruch
1. Schritt: Ganze in Bruch umwandeln.
2. Schritt: Zähler bestimmen.
3. Schritt: Notieren.
3 2
_
​ 3 ​+ _​ 3 ​
15
3. 2 ​ _7 ​= __
​ 7  ​
c)
2
Ergänze die fehlenden Brüche, die Zeichnungen und die gemischten Zahlen.
14
____
​ 
 
 ​=
5
2
4
22
5
9
____ 
​ ____ 
 ​​ 
 ​=
11
3
8
____
​ 
  
​= 1 ​ _8 ​​ _3 ​=
8
3
7
3
9
1
​ ____ 
 ​
b) ​ _5 ​=
17
2
​ ____  
​
5
d) __
​ 7  ​=
28
2
4
6
12
1
1
4
19
9
6
____ 
​ ____ 
 ​​ 
 ​=
2
7
____
​ 
  
​​ _4 ​=
3
4
Wandle in eine gemischte Zahl um.
a) _​ 4 ​=
c) __
​ 6  ​=
2
4
3
15
a) 3 ​ _4 ​= ____
​ 
 
 ​
5
c) 3 ​ _5 ​= ____
​ 
  
​
​ ____ 
 ​
7
4
2
1
1
​ ____ 
 ​
6
3
​ ____  
​
4
Wandle in einen Bruch um.
​ ____ 
 ​
5
3
17
5
3
31
b) 4 ​ _7 ​= ____
​ 
 
 ​
7
5
11
d) 1 ​ _6 ​= ____
​ 
 
 ​
6
Bruchteile berechnen
1. Schritt: Das Ganze durch den Nenner teilen.
2. Schritt: Das Zwischenergebnis mit dem Zähler
multiplizieren.
3. Schritt: Notieren.
3
Beispiel: Wie viel sind _5 von 10 Eiern?
1. Schritt 2. Schritt
67999899990 67999899990
10 Eier
:5
2 Eier
·3
6 Eier
3
3. Schritt: _5 von 10 Eiern sind 6 Eier.
1
Berechne den Bruchteil:
2
a) _6 von 6 Flaschen (F)
3
b) _4 von 12 Flaschen
2
c) _3 von 18 m
3
d) _5 von 60 kg
2
e) _7 von 56 ø
5
f) __
12 von 84 min
6
g) _9 von 126 g
3
h) _7 von 105 km
2
:6
6F
·2
1F
:4
12 F
:3
:7
36 kg
: 12
56 ø · _7 = 16 ø
16 ø
5
84 min · __
12 = 35 min
·5
7 min
:9
126 g
2
·2
8ø
84 min
3
60 kg · _5 = 36 kg
·3
35 min
6
126 g · _9 = 84 g
·6
14 g
:7
84 g
3
105 km · _7 = 45 km
·3
15 km
45 km
In der Sprache tauchen häufig Brüche auf. Ordne die Angaben den Sätzen zu.
1 Das Wasser ist nur ei-
nen halben Meter tief.
50 cm
2 Du bist eine Viertelstunde zu spät.
15 min
ren ein Drittel schlecht.
50 cm
500 g
250 mø
1 kg
15 min
Welche Angabe bleibt übrig? 250 mø
3 Von 3 kg Kirschen wa-
1 kg
12 m
12 kg
56 ø
2
18 m · _3 = 12 m
·2
:5
105 km
9F
6m
60 kg
3
12 F · _4 = 9 F
·3
3F
18 m
2
6 F · _6 = 2 F
2F
4 Bitte ein halbes Kilo
Hackfleisch.
500 g
Bilde dazu eine eigene Aussage.
Man nehme einen Viertelliter Milch. (Beispiel)
29
Erweitern und kürzen
2
Beispiel: _3 erweitern mit 2
Beim Erweitern werden Zähler und Nenner mit derselben Zahl multipliziert,
der Wert des Bruchs bleibt gleich.
1. Schritt: Zähler und Nenner mit der gleichen Zahl multiplizieren
2. Schritt: Notieren
Beim Kürzen werden Zähler und Nenner durch dieselbe Zahl geteilt.
Auch hier bleibt der Wert des Bruchs gleich.
1. Schritt: Zähler und Nenner durch die gleiche Zahl teilen
2. Schritt: Notieren
2·2
___
4
= _6
3·2
2
_
4
= _6
3
6
Beispiel: _9 kürzen mit 3
6:3
___
2
= _3
9:3
6
_
2
= _3
9
1
Bestimme die Zahl, mit der erweitert wurde.
4· 3
12
______
= __
15
5· 3
7· 5
35
______
= __
15
3· 5
9· 9
81
______
= __
99
11 · 9
3 · 10
30
______
= __
80
8 · 10
12 · 4
48
______
= __
60
15 · 4
17 · 5
85
_______
= __
110
22 · 5
3 · 12
36
______
= __
96
8 · 12
7 · 12
84
______
= ___
108
9 · 12
2 · 30
60
______
= ___
210
7 · 30
31 · 5
155
______
= ___
55
11 · 5
121 : 11
11
_______
= __
12
132 : 11
2
Mit welcher Zahl wurde gekürzt?
18 : 6
3
_______
= _4
24 : 6
36 : 2
18
_______
= __
20
40 : 2
50 : 10
5
_______
= _7
70 : 10
49 : 7
7
_______
= _8
56 : 7
56 : 4
14
_______
= __
19
76 : 4
49 : 7
7
_______
= __
12
84 : 7
54 : 9
6
_______
= _9
81 : 9
90 : 45
2
_______
= _5
225 : 45
3
Du kannst auch
schrittweise kürzen:
:2
54
__
96
Erweitere mit den angegebenen Zahlen.
=
:3
27
__
48
:2
7
_
8
5
_
9
mit 3
mit 5
mit 8
7 · 3 __
21
___
=
35
__
56
__
8·3
15
__
27
24
40
25
__
45
64
40
__
4
Kürze so weit wie möglich.
36
a) __
48 =
36 : 12 _
3
____
=
72
b) __
90 =
72 : 18 _
4
____
=
48 : 12
90 : 18
4
5
72
216
9
216 : 24 __
_____
c) ___
=
240 =
2
__
11
6
__
33
10
__
55
240 : 24
16
__
88
210
d) ___
330 =
6
__
13
25
__
31
30
18
__
39
75
__
93
30
__
65
125
___
155
10
210 : 30 __
7
_____
=
330 : 30
11
48
___
104
200
___
248
90
90 : 15
6
_____
__
e) ___
165 = 165 : 15 = 11
147
147 : 21 _
7
_____
f) ___
189 = 189 : 21 = 9
=
:3
9
__
16
Test: Brüche 1
1
Berechne den Anteil.
2
_
​ 3 ​von 21 Autos
11
__
​ 12 ​ von 96 Autos
25
__
​ 27 ​ von 108 Autos
14 Autos
88 Autos
100 Autos

3
_
​ 4 ​von 12 kg = 9 kg


Gib in Minuten an.
2
_
​ 3 ​ h = 40 min
7
__
​ 10  ​ h = 42 min

3
11
​ __
15 ​  h = 44 min


Schreibe als gemischte Zahl.
3
4
25
__
​ 7  ​= 3 ​ _7 ​
= 2 ​ _4 ​
4
2


8
__
​ 13  ​von 52 Stunden = 32 h
14
__
​ 15 ​von 60 Litern = 56 ø
2


169
4
___
​ 33  ​= 5 ​ __
33  ​ 


Schreibe als Bruch.
14
5
4 ​ _3 ​= __
​ 3  ​

5
12
257
7 __
​ 35 ​ = ___
​ 35  ​


Erweitere.
105
35
__
​ 48 ​ mit 3: ___
​ 144  ​
20
4
__
​ 12  ​mit 5: __
​ 60 ​ 
3
12
_
​ 8 ​mit 4: __
​ 32 ​ 

6
53
6 ​ _8 ​= __
​ 8  ​


Kürze so weit wie möglich.
12 3
__
​ 8  ​= _​ 2 ​
32 2
__
​ 48 ​ = _​ 3 ​

Bronze:
Silber:
Gold:
2
48
___
​ 120  ​ = _​ 5 ​


(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 77.)
31
Gleichnamige Brüche addieren und subtrahieren
Beispiel
1. Schritt: Zähler addieren (+) oder subtrahieren (–) und
den Nenner beibehalten
2. Schritt: wenn möglich, kürzen
3. Schritt: wenn möglich, in eine gemischte Zahl verwandeln
4. Schritt: Notieren
Brüche sind gleichnamig,
wenn sie den gleichen
Nenner haben.
1
12
12
16
1.
11 + 5
____
12
2.
16 : 4 _
4
____
=
3.
4
_
3
4.
5
11 __
1
__
+ = 1_
= __
12
12 : 4
3
1
= 1 _3
12
12
3
Notiere die dargestellte Additionsaufgabe.
a)
b)
9
5
4
__
+ __ = __
10
2
10
c)
3
2 _
_1 + _
=
4
10
4
d)
13
6
7
__
+ __ = __
4
16
16
3 5
2 _
_
+ =_
16
6
6
6
Notiere die dargestellte Subtraktionsaufgabe.
a)
b)
8
4
4
1
__
– __ = __ = _
12
3
5
11 __
__
+
12
12
3
c)
5 _
2 3 1
_
– =_=_
6
6
6
d)
7 _
1 6 2
_
– =_=_
2
9
9
9
6 _
2 4 1
_
– =_=_
3
8
8
8
2
Berechne. Kürze, wenn möglich, und schreibe als gemischte Zahl.
7
__
_1
9
__
7
2
__
11
a) __
+
=
11 11
3 4
b) _5 + _5
= 5 =15
6
13 __
c) __
14 – 14
= 14 = 2
25 __
5
30 __
15
7
__
_
d) __
16 + 16 = 16 = 8 = 1 8
16
24 __
e) __
11 – 11
8
= __
15
41 __
f) __
16 – 16
13
5
26 __
_
= __
16 = 8 = 1 8
17 _
4
g) __
5 –5
5
3
7
15
1
__
__
__
__
h) __
14 + 14 + 14 = 14 = 1 14
23 __
3 __
7
13
2
__
__
i) __
11 – 11 – 11 = 11 = 1 11
36
24 __
k) __
25 + 25
53 __
27
l) __
24 – 24
13
3
_
= __
5 = 25
37 __
18
55 __
3
11
__
_
j) __
40 + 40 = 40 = 8 = 1 8
4
2
_
11
60 __
12
2
_
= __
25 = 5 = 2 5
13
26 __
1
__
= __
24 = 12 = 1 12
Ergänze.
4
3
7
_
a) _8 + ____
8 =8
32
7
_
5
6
11 __
____
b) __
12 – 12 = 12
6
8
2 _
_
c) ____
9 +9=9
14
3
11
__
____
d) ____
13 – 13 =
13
Brüche gleichnamig machen
Brüche kann man nur addieren (+)
oder subtrahieren (–), wenn sie
den gleichen Nenner haben.
1. Schritt:Vielfaches des ersten Nenners suchen
2. Schritt:Vielfaches des zweiten Nenners suchen
3. Schritt:kleinstes gemeinsames Vielfaches (kgV)
bestimmen
4. Schritt:Brüche auf den gleichen Nenner bringen
2
1
Beispiel: _​ 8 ​und _​ 6 ​gleichnamig machen
1.Vielfaches von 8: 8, 16, 24, 32, …
2. Vielfaches von 6: 6, 12, 18, 24, 30, …
3. kgV = 24
2
6
1
4
4.​ _8 ​= __
​ 24  ​;  _​ 6 ​= __
​ 24  ​ 
1
Mache die Brüche gleichnamig.
3
4
a)​ _8 ​und _​ 6 ​
3
3
b)​ _5 ​und _​ 4 ​
1.
Vielfaches des 1. Nenners
8, 16, 24, 32
5, 10, 15, 20
2.
Vielfaches des 2. Nenners
6, 12, 18, 24
8, 8, 12, 16, 20
3.
KgV bestimmen
24
20
4.
Brüche auf den gleichen Nenner
bringen.
9 4 16
3
_
​ 8 ​= __
​ 24  ​;  _​ 6 ​= __
​ 24 ​ 
3 12 _
3 15
_
​ 5 ​= __
​ 20 ​;  ​ 4 ​= __
​ 20 ​ 
5
7
c)​ _8 ​und __
​ 12  ​
7
3
_
d)​ __
10  ​und ​ 4 ​
3
5
e)​ _7 ​und _​ 8 ​
1.
8, 16, 24, 32
10, 20, 30
7, 14, 21, 28, 35, 42, 49, 56
2.
12, 24
4, 8, 12, 16, 20
8, 16, 24, 32, 40, 48, 56
3.
24
20
56
4.
5 15 __
7
14
_
​ 8 ​= __
​ 24 ​;  ​ 12  ​= __
​ 24 ​ 
7
14 3 15
__
​ 10  ​= __
​ 20 ​;  _​ 4 ​= __
​ 20  ​
3 24 _
5 35
_
​ 7 ​= __
​ 56 ​;  ​ 8 ​= __
​ 56  ​
2 Brüche kann man am besten vergleichen, wenn sie gleichnamig sind. Vergleiche die Brüche.
Setze passend < oder > ein.
2
4
a)​ _3 ​ > _​ 7 ​ , weil
2
14
4
12
​ _3 ​= __
​ 21 ​> _​ 7 ​= __
​ 21 ​
5
7
< __
d)​ __
​ 20  ​  , weil
18  ​
5
50
63
7
__
​ 18  ​= ___
​ 180  ​ < __
​ 20  ​ = ___
​ 180  ​ 
9
5
> _
b)​ __
​ 8 ​ , weil
11  ​
5
7
c)​ _6 ​ > __
​ 10  ​ , weil
9
72 5 55
__
​ 88 ​> _​ 8 ​= __
​ 88 ​ 
​ 11  ​= __
5 25 __
7
21
_
​ 30 ​ > ​ 10  ​= __
​ 30 ​ 
​ 6 ​= __
3
5
e)​ _7 ​ < __
​ 11  ​ , weil
15
10
= __
f)​ __
​ 8  ​ , weil
12 ​
3 33 __
5
35
_
​ 7 ​= __
​ 77 ​ < ​ 11  ​= __
​ 77 ​ 
10 30
15 30 __
__
​ 12 ​= __
​ 24 ​ = ​ 8  ​= __
​ 24 ​ 
33
Ungleichnamige Brüche addieren und subtrahieren
Beispiel
5
1. Schritt:Brüche gleichnamig machen
2. Schritt:Zähler addieren (+) oder subtrahieren (–), Nenner beibehalten
3. Schritt:wenn möglich kürzen und in eine gemischte Zahl verwandeln
1
5
5
10
3
1
2
3
10
b)​ _5 ​+ _​ 3 ​
15
1.
= __
​ 18 ​+ __
​ 18 ​
2.
= __
​ 18 ​ 
3.
= 1 ​ __
18  ​
14 2
__
​ 9  ​– _​ 6 ​
1.
10 11
__
​ 14 ​+ __
​ 14 ​ 
6
28
__
​ 18  ​– __
​ 18  ​
2.
10 + 11 __
21
____
​  14   
 
​= ​ 14 ​
28 – 6 __
22
____
​  18   
​ = ​ 18 ​ 
3.
21 3
1
__
​ 14 ​= _​ 2 ​= 1 ​ _2 ​
22 11
2
__
​ 18 ​ = __
​ 9  ​= 1 ​ _9 ​
6
13
13
26
5
5
15
= __
​ 30 ​ – __
​ 30 ​ 
2.
= ​ __
30 ​ 
40
1
= ​ _5 ​
21
3
5
= ​ __
30  ​ 
11
1
9
14
​ 30  ​ 
= __
​ 30 ​ – __
= ​ __
36 ​
= 1 ​ __
36 ​ 
= 1 ​ __
72  ​
3.
21
47
= __
​ 72 ​
3
7
__
h)​ __
15  ​– ​ 10  ​
__
= ​ __
36 ​ + ​ 36 ​ 
73
11
7
26
33
9
= __
​ 35 ​ 
__
g)​ __
18 ​+ ​ 12  ​
= __
​ 72 ​ + __
​ 72 ​ 
30
4
13
11
f)​ _9 ​+ __
​ 24 ​ 
9
__
= ​ __
35 ​ – ​ 35  ​ 
= _​ 2 ​
1.
2
2
= ​ _8 ​
7
6
d)​ _7 ​– __
​ 35  ​ 
= _​ 8 ​– _​ 8 ​
= __
​ 15 ​
25
2
c)​ _4 ​– _​ 8 ​
__
= ​ __
15  ​+ ​ 15 ​
__
e)​ __
15 ​– ​ 10  ​
1
= ​ _6 ​
Addiere zwei benachbarte Zahlen und trage das Ergebnis in das Feld darüber ein.
a)
1
10 ​ _4 ​
29
__
​ 12 ​ 
15
__
​ 4  ​
7
_
​ 3 ​
1
_
​ 1 ​
17
__
​ 12 ​
5
_
​ 6 ​
3
_
​ 2 ​
1
_
​ 2 ​
3
1
_
​ 1 ​
3
_
​ 4 ​
1
3
_
​ 8 ​
2
_
​ 3 ​
5
__
​ 12  ​
​ _4 ​
3
_
​ 2 ​
3
_
​ 2 ​
5
_
​ 3 ​
7
__
​ 12  ​
1
_
​ 3 ​
b)
49
__
​ 12 ​ 
74
__
​ 12 ​
34
11
Berechne. Kürze, wenn möglich und schreibe als gemischte Zahl.
a)​ _9 ​+ _​ 6 ​
h
​ _7 ​+ __
​ 14 ​ 
3
__
​ 16  ​
1
_
​ 4 ​
1
​ _6 ​
1
__
​ 12  ​
1
_
​ 8 ​
3
_
​ 8 ​
3
__
​ 16  ​
1
__
​ 16  ​
3
3
_
​ 4 ​
​ _4 ​
3
__
​ 16  ​
3
__
​ 16  ​
1
_
​ 8 ​
3
_
​ 8 ​
3
_
​ 8 ​
1
​ __
16  ​
3
__
​ 16  ​
1
_
​ 8 ​
1
__
​ 16  ​
Brüche mit ganzen Zahlen multiplizieren (vervielfachen)
1. Schritt:Zähler mal ganze Zahl, Nenner beibehalten
2. Schritt:wenn möglich, kürzen
3. Schritt:Berechnen
4. Schritt:wenn möglich, in eine gemischte Zahl verwandeln
1
2
2
=
4
·​ _5 ​
=​ _5 ​
c)
7 · 6
= ____
​  8   
​ 
7 · 6 3
= ____
​  8   
​ 
= ___
​  4   ​ 
2.
= ___
​  4    ​
3.
= __
​ 2  ​
4.
= 10 ​ _2 ​
2
10 · 3
5
10 · 3
4
15
21
= __
​ 4  ​
1
3
= 3 ​ _4 ​
5
1
5 ·​ _6 ​
10 · ​ _8 ​
1.
b)
=
3
7
​ _4 ​ · 6
Notiere unter jeder Abbildung die passende Aufgabe.
a)
Beispiel
=​ _6 ​
d)
3
4 · ​ _5 ​
2
2
2 ​ _5 ​
=
3
3 · ​ _8 ​
=
1
1 ​ _8 ​
Berechne. Kürze, wenn möglich, und schreibe das Ergebnis als gemischte Zahl.
2
a) _​ 5 ​ · 7 =
2 · 7
14
4
​ ___
​ = __
​ 5  ​= 2 ​ _5 ​
5   
10
5
7 · 10 __
70
___
d) 7 · ​ __
​ = ​ 13 ​ = 5 ​ __
13 ​ = ​  13   
13  ​
3
4
b) _​ 7 ​ · 8 =
4 · 8 32
4
___
​  7    ​= __
​ 7  ​= 4 ​ _7 ​
3
e) _​ 4 ​ · 6 =
3 · 6 9
1
___
​  4    ​= _​ 2 ​= 4 ​ _2 ​
3
2
5
c) 3 · ​ _8 ​ =
4
f) 6 · ​ _9 ​ =
3 · 5 15
7
___
​  8    ​= __
​ 8  ​= 1 ​ _8 ​
2
6 · 4 8
2
___
​  9   ​ = _​ 3 ​= 2 ​ _3 ​
3
Wie viel der Zutaten braucht man, um die dreifache Menge des Cocktails zuzubereiten?
3
9
1
3
2
6
1
Ananassaft:
3 ·​ _4 ​= _​ 4 ​= 2 ​ _4 ​ ø
Kirschsaft:
3 · ​ _4 ​= _​ 4 ​ ø
1
Zitronensaft: 3 ·​ _5 ​= _​ 5 ​= 1 ​ _5 ​ ø
35
Brüche mit Brüchen multiplizieren
1. Schritt:Zähler mal Zähler, Nenner mal Nenner
2. Schritt:wenn möglich, kürzen
3. Schritt:Berechnen
4. Schritt:wenn möglich, in eine gemischte Zahl verwandeln
Beispiel
1
Berechne. Kürze, wenn möglich, und schreibe das Ergebnis als
gemischte Zahl.
5 3
5 · 3 1 5
a) ​ _9 ​ · ​ _8 ​ = ___
​ 9 · 8  ​= __
​ 24  ​ 
3
4 5
b) ​ _7 ​ · ​ _8 ​ =
1
4 9
c) ​ _3 ​ · ​ _8 ​ =
1
24 15
e) __
​ 5  ​ · ​ __
32  ​ =
2
5
8
4 5
_
​ 5 ​ ·_​ 6 ​
​ _7 ​ · ​ _4 ​
8 · 5
= ___
​ 5 ·6  ​
= ___
​ 7 · 4  ​
8 · 5
= ___
​ 5 ·6  ​
10
__
​ 7  ​
2
_
​ 3 ​
1.
= ___
​ 7 · 4  ​
2.
3.
=
4.
= 1 ​ _7 ​
2
4 · 5
24 · 5 1
1
1
=
3
3
5
4 · 5
___
​ 7 · 8  ​= __
​ 14  ​
2
1
4 · 9
3
3
35 18
d) __
​ 12 ​  · ​ __
25 ​  =
1
_
_
​ ___
 ​= ​ 2 ​= 1 ​ 2 ​
3 · 8 
2
3
1
9
24 · 15 3 _
1
____
​ 5 · 32  
​= ​ 4 ​= 2 ​ _4 ​
7
35 · 18 3 __
21
1
__
____
​ 
 
 ​= ​ 10 ​= 2 ​ 10  ​
212 · 25 5
2 9
9 1___
5 · 9 3 _
5 __
3
1
_
f) 1 ​ _3 ​ · ​ __
= ​   ​= 1 ​ _2 ​
10  ​ = ​ 3 ​ · ​ 10  ​=1 ​ 3 · 10  ​ 
2 2
4
Berechne die Anteile der Größen.
1
2 1
2 · 1
1
_
​ 3 ​ ∙ ​ _4 ​Stunde = ___
​ 3 · 4  ​ Stunde = _​ 6 ​Stunde = 10 Minuten
a) Zwei Drittel von einer Viertelstunde:
2
1
3
b) Ein Sechstel von einem _​ 4 ​Meter:
2
1 1
1
_
​ 4 ​ · ​ _2 ​ kg = _​ 8 ​ kg = 125 g
c) Ein Viertel von einem halben Kilogramm:
2
d) Vier Fünftel von einem halben Liter:
h
3
1 3
1
_
​ 6 ​ ∙ ​ _4 ​m = _​ 8 ​ m = 12,5 cm
4 1
2
_
​ 5 ​ ∙ ​ _2 ​ ø = _​ 5 ​ø = 200 mø
1
Ergänze die Rechenschlange. Kürze, wenn dies möglich ist.
5
_
​ 6 ​
· 3
1
5
_
​ 2 ​
· ​ _6 ​
5
__
​ 12  ​
· 4
1
5
_
​ 3 ​
· ​ _5 ​
1
_
​ 3 ​
· 7
8
__
​ 45  ​ 
36
4
· ​ _9 ​
2
_
​ 5 ​
5
· ​ _7 ​
42
__
​ 75 ​ 
3
· ​ _5 ​
14
__
​ 15 ​
2
· ​ _5 ​
7
_
​ 3 ​
Brüche dividieren
1. Schritt: 1. Bruch notieren, dann mit dem Kehrwert
des 2. Bruchs malnehmen
2. Schritt: wenn möglich, kürzen
3. Schritt: Berechnen
4. Schritt: wenn möglich, in eine gemischte Zahl verwandeln
Beispiel
32 __
16
__
:
15
1
Berechne. Kürze, wenn möglich, und schreibe das Ergebnis als
gemischte Zahl.
5 8
a) _9 : _3
6 9
b) _5 : __
10
5 · 3 1 __
5
= _5 · _3 = ___
9 8 3 9 · 8 = 24
35 __
55
35 __
35 · 18 3 __
18 7____
21
__
c) __
12 : 18 = 12 · 55 = 12 · 55 11= 22
2
4 _
2
_
:
11
32
5
11
7
4
7
1.
__
= __
15 · 16
= _5 · _2
2.
= ____
15 · 16
2 32 · 11
= ___
5·2
3.
22
= __
15
4.
= 1 __
15
2
1
4·7
1
14
= __
5
7
4
= 2 _5
10 2___
6 ·10 2 _
4
_1
= _6 · __
5 9 =1 5 · 9 3= 3 = 1 3
Der Kehrwert ergibt sich
durch Vertauschen von
Zähler und Nenner.
5 __
15
5 __
32 1____
5 · 32 4 _
4
__
d) __
24 : 32 = 24 · 15 =3 24 · 15 3= 9
2
2
4
5
9
5·9
7
12
1
3
15
3
_
e) 1 _3 : _9 = _3 · _4 = ___
= __
4 = 34
1 3·4
7 · 12 3 3
_ · __ = ___ = _ = 3
3 7
g) 1 _4 : __
12 = 4 7 1 4 · 7 1 1
2
1
9
3
8
3
9·8
2
6
f) 2 _4 : _8 = _4 · _3 = ___
=_=6
1 4·3 1 1
1
1
4 _
4
_
4·4
___
16
__
1
__
f) 1 _3 : 1 _4 = 3 · 5 = 3 · 5 = 15 = 1 15
Schreibe jeweils eine Divisionsaufgabe und berechne.
1
a) 1 _2 ø Orangensaft sollen auf 4 Gläser verteilt werden. Wie viel Saft ist in einem Glas?
2
4
3
1
3
3 1 3
_
: 4 = _·_ = _
2
1
b) 5 Pizzen werden in _3 –Stücke aufgeteilt.
Wie viele Stücke gibt das?
5·3
5 : _3 = 5 · _1 = ___
1 = 15
8
3
Antwort: Es sind _8 ø pro Glas.
Antwort: Es sind 15 Stücke.
c) In einer Bäckerei werden in 2 _21 Stunden 240 Brezeln hergestellt. Wie viele Brezeln sind das pro
Stunde?
d) 2 _2 kg Wurst wird in Packungen zu je _4 kg abgepackt. Wie viele Packungen ergibt das?
5
2
48
240 · 2
240 : _2 = 240 · _5 = ____
= 96
5
1
Antwort: Es sind 96 Stück pro Stunde.
1
1
1
1
5 4
2 _2 : _4 = _2 · _1 = 10
Antwort: Es sind insgesamt 10 Packungen.
37
Textaufgaben
1 Für einen Kuchen benötigt man: Die Hälfte des Mehls, die Hälfte des
Zuckers, ein Viertel der Haselnüsse, ein Zehntel der Speisestärke.
Gib die Zutaten in Gramm an.
500 g
Zucker:
Haselnüsse: 100 g
Speisestärke: 60 g
Mehl:
250 g
Raum für Nebenrechnungen:
2
2
a) An einem Marathon nehmen 650 Läuferinnen und Läufer teil. _​ 5 ​davon
1
schaffen den Marathon in unter 3 ​ _2 ​Stunden.
Das sind insgesamt 260
Läufer/-innen.
3
b) Die Strecke ist 42 Kilometer lang, __
​ 10  ​davon gehen durch den Wald.
Die Länge der Waldstrecke beträgt 12,6
Kilometer.
c) Der Marathon beginnt um 10:45 Uhr. Der schnellste Läufer kommt nach
1
1
2 ​ _4 ​Stunden ins Ziel, der letzte nach 5 ​ _2 ​Stunden.
13:00 Uhr
Ankunftszeit 1. Läufer:
Ankunftszeit letzter Läufer: 16:15 Uhr
3
1
2
2
1
Niklas isst _​ 5 ​Pizza Salami, _​ 7 ​Pizza Sizilia, _​ 5 ​Pizza Diabolo und _​ 7 ​Pizza Spinat.
a) Hat er mehr oder weniger als eine ganze Pizza gegessen?
3 3
1
Rechnung: _​ 5 ​+ _​ 7 ​= 1 ​ __
35  ​ 
Antwort:
Er hat mehr als eine ganze Pizza gegessen.
1
1
b) 4 ​ _2 ​Pizzen werden in _​ 4 ​ -Stücken verkauft. Ein Stück kostet 1,50 €.
Wie viel Umsatz macht die Pizzeria, wenn alle Stücke verkauft werden?
Rechnung: 18 Stücke à 1,50 € = 27 €
Antwort:
Die Pizzeria macht 27 € Umsatz.
4 Manuela übt fünfmal
in der Woche eine halbe Stunde Englisch. Cem übt
1
zweimal in der Woche 1 ​ _2 ​Stunden.
a) Wer übt mehr?
Rechnung: Manuela: 2,5 Std., Cem 3 Std.
Antwort:
Cem übt mehr.
1
b) Karin will in der Woche 2 ​ _2 ​Stunden lernen und die Zeit auf drei Tage verteilen,
an denen sie gleich lang übt. Wie viel Zeit muss sie an den drei Tagen jeweils
einplanen?
1
5
1
5
Rechnung: 2 _​ 2 ​: 3 = _​ 2 ​ · ​ _3 ​= _​ 6 ​
Antwort:
38
5
Sie muss 3-mal _​ 6 ​einer Stunde (= 50 Minuten) üben.
Test: Brüche 2
1
Berechne. Kürze, wenn möglich und schreibe als gemischte Zahl.
13 8
__
​ 15 ​+ _​ 5 ​=
5 5
_
​ 6 ​+ _​ 9 ​=
13 24 __
37
7
__
​   ​+ __
​   ​ = ​   ​= 2 ​ __  ​
15
15
7
15
15

4
13
12
6
4

7
1
__
​ 12  ​– _​ 4 ​=
1
12
3
1
12 3 3

4
2
4
4
4



4
8 · 4
8
6
8
24
24

2

1
1
2 · 3
1

3

3
1
1 3
1 · 3
1
Silber:
5
3 · 5

1
24
48
16
48
48
48

7
5
35

218 · 13
26
26

15
21
7
1
2
3 15 ·21 3
9
9

3 ​ _4 ​ · 4 ​ _3 ​=
3
91
13 14 13 · 14 7 __
1
__
​    ​ · ​ __  ​= ____
​ 
  
​= ​    ​= 15 ​ _ ​
1
3

1
Gold:

2
3
2
42
5
14 35 14 · 35 __
14
__
​   ​ · ​ __ ​ = ____
​ 
  
​= ​    ​= 1 ​ _ ​
4 12 ·10 2 8
4
3
4
2
4 · 3
6
6

1
2 ​ _5 ​: 2 ​ _3 ​=
2
23 1 23 _
46
2 23 · 2 __
1
__
​    ​: _​   ​= __
​    ​ · ​   ​= ____
​    
​= ​    ​= 9 ​ _ ​

42
14 21
__
​ 15 ​: __
​ 35 ​ =
4 ​ _5 ​: _​ 2 ​=
3 3 3 4 3 · 4
_
​   ​: _​   ​= _​   ​ ·_​   ​= ___
​    ​= 4
Bronze:
42
3
1
3 : _​ 4 ​=
4
10
5

51
25
17 · 27 __
____
​ 
  
​= ​   ​ = 1 ​ __ ​
5 8 5 · 8 _
8
2
_
​   ​ · ​ _ ​= ___
​    ​= ​   ​= 2 ​ _ ​
3
12
17 27
__
​ 18 ​ · ​ __
13 ​ =
1 ​ _3 ​ · 1 ​ _5 ​=
1
12
6 1
6
_
​   ​ · ​ _ ​= __
​    ​
1
1
2
12
6
_
​ 7 ​: 5 =
12
79
65 17 ___
130 51 __
31
__
​   ​– __
​   ​= ​    ​– __
​   ​ = ​   ​= 1 ​ __ ​ 
24
1

4
3
17
11 · 12 3 33
12

__
2 ​ __
24 ​ – 1 ​ 16  ​=
5 21
5 · 21 7 _
7
__
​    ​ · ​ __ ​= ____
​ 
 
 ​ 
= ​   ​
32
3 2 3 · 2
_
​   ​ · ​ _ ​= ___
​    ​= 1
1
3

5 10
__
​ 12  ​: __
​ 21 ​=
1 ​ _2 ​ · ​ _3 ​=
1
8 · 7
14
____
​    ​ = __
​   ​ 
3 7 3 · 7 __
21
_
​   ​ · ​ _ ​= ___
​    ​= ​   ​ 
60
3
60
19
39 20 __
__
​   ​= ​   ​ 
​   ​– __
60 12 12
60
2
60
13 10
__
​ 14 ​– __
​ 21 ​=
2
3 4
_
​ 8 ​: _​ 7 ​=
3

2
63
2
18
8 7
__
​ 11  ​ · ​ __
12  ​=
9 · 7
1
18
3 · 16 _
6
___
​     
​ = ​   ​= 6
11
4 · 5 20
___
​    ​= __
​   ​
18
3
4 5
_
​ 9 ​ · ​ _7 ​=
8
9
60
5
68 93 __
161
17 31 __
__
​    ​+ __
​    ​= ​   ​ + __
​   ​ = ​    ​= 13 ​ __  ​
43 28 __
43 14 __
71
17
__
​    ​= ​   ​ + __
​ 18 ​ = ​   ​= 3 ​ __ ​
​   ​ + __
18
60
5 ​ _3 ​+ 7 ​ _4 ​=
​ _8 ​ · 16 =
3 ·2
6
___
​     ​= __
​    ​
5
19
13 11 __
52 33 __
__
​    ​– __
​    ​= ​   ​– __
​   ​= ​   ​ 
3
__
​ 11  ​ · 2 =
11

2 ​ _6 ​– 1 ​ _8 ​=
15 3 15 _
6 9
1
__
​    ​– _​   ​= __
​    ​– ​   ​= _​   ​= 2 ​ _ ​
25 5 5
33
8
__
​   ​– __
​    ​= __
​   ​= __
​    ​
3 ​ _4 ​– 1 ​ _2 ​=
4
18
11
2
__
​ 20 ​ – __
​ 15  ​=
3
4
1
7
__
​    ​= __
​    ​= _​   ​
​    ​– __
12
18
_
2 ​ __
18  ​+ 1 ​ 9 ​=
19 10 __
19 20 __
39
1
__
​   ​+ __
​    ​= ​   ​+ __
​ 12 ​ = ​ 12 ​ = 3 ​ _4 ​
12
79
19
44 35 __
__
​   ​+ __
​   ​= ​   ​= 1 ​ __ ​ 
15 10
7
__
​ 18 ​= 1 ​ __  ​
​   ​+ __
7
_
1 ​ __
12  ​+ 1 ​ 6 ​=
11
7
__
​ 15 ​ + __
​ 12  ​=
5
1
5 · 1
5
5
3 14 · 3 _
6
14 7 14 _
1
__
​    ​: _​   ​= __
​    ​ · ​   ​= ____
​    
​= ​   ​= 1 ​ _ ​

5
3
5
7
5 · 7 1
5
5

(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 77.)
39
Darstellung von Zuordnungen
Bei einer Zuordnung wird einer Größe oder Zahl
eine zweite Größe oder Zahl zugeordnet.
Die Zuordnung kann durch eine Tabelle oder
ein Koordinatensystem dargestellt werden.
Beispiel
Temperaturverlauf
Uhrzeit (h)
Temperatur (°C)
1222222222222223222222222222225
Zahlen im Koordinatensystem darstellen
1. Schritt:Koordinatensystem mit x- und y-Achse
zeichnen, Achsen beschriften
2. Schritt:Wertepaare eintragen
8
14
9
15
10
17
11
20
12
24
13
25
Hochachse
oder
y-Achse
Zahlen ablesen
1. Schritt:Wert der x-Achse ablesen und notieren
2. Schritt:Wert der y-Achse ablesen und notieren
1222222222222223222222222222225
Rechtsachse oder x-Achse
1
Die Bevölkerungsentwicklung in Deutschland:
Ergänze die Tabelle.
83
2
Berechne. Zeichne zu der Tabelle ein
passendes Schaubild.
Preise für Kartoffeln
Bevölkerung in Mio.
82
Gewicht
1 kg
2 kg
2,5 kg
4 kg
81
Preis
1,20 €
2,40 €
3 €
4,8 €
80
79
78
5
77
Preis in Euro
76
4
75
74
73
Jahr
1960
1980
2000
2020
2040
3
2060
2
Jahr
1960 1970 1990 2000 2040 2050
Bevölkerung
73,1
in Mio.
78
79,8
82
1
75
78,5
Gewicht in kg
1
3 Ein Tretbootverleih verlangt für jede
angefangene halbe Stunde 1 €.
4
Berechne die Gebühren zu den vorgegebenen
Zeiten und übertrage die Werte in das
Koordinatensystem.
2
3
4
5
Preis in €
3
2
Zeit in min
20
30
40
70
100
Preis in €
1
1
2
3
4
1
Zeit in Min
20
40
40
60
80
100
Darstellung von Zahlen in Diagrammen
Mit Hilfe von Diagrammen lassen sich Zahlen,
Zeit- und Größenangaben veranschaulichen.
3
2
1
PreisPreis
(€) (€)
3
2
Gewicht
Gewicht
(g) (g)
1
O
O200 600
200 1000
600 1000
Säulendiagramm
Säulendiagramm Balkendiagramm
BalkendiagrammKreisdiagramm
KreisdiagrammStreifendiagramm
Streifendiagramm Koordinatensystem
Koordinatensystem
Die Angaben sind
durch senkrechte
Balken dargestellt.
Die Werte werden an
der y-Achse abgelesen.
Die Angaben sind durch
waagerechte Balken
dargestellt. Die Werte
werden an der x-Achse
abgelesen.
1 Bei den Olympischen Spielen in Turin wurden die Medaillen gezählt. Lies aus dem Schaubild die Anzahl
der Medaillen der einzelnen Nationen ab und berechne die Summe aller Medaillen.
Nation
Gold
Silber
Bronze
Summe
Kanada
7
10
7
24
USA
9
9
7
25
Deutschland
11
12
6
29
Russland
8
6
8
22
Österreich
9
7
7
23
2
Anzahl Medaillen
12
10
8
6
4
2
0
Kanada
USA
Deutschland
Russland
Gold
In einer Schule wurden Taschen gewogen.
Österreich
Silber
Bronze
Anzahl Taschen
70
a) Lies aus der Grafik die ermittelten Werte ab
und trage alle in die Tabelle ein.
60
b) Es wurden insgesamt 150
40
Taschen gewogen.
50
30
Gewicht der
Tasche in kg
Anzahl
3
unter
3,0
15
3,0 bis
3,5
3,5 bis
4,0
60
55
über
4,0
20
20
0
Gewicht
in kg
10
unter 3,0 3,0 bis 3,5 3,5 bis 4,0
über 4,0
Veranschauliche die Längen der folgenden Flüsse im Diagramm. Runde die Längen auf Tausender.
Amazonas: 6 437 km ≈ 6 000 km
Elbe:
1 165 km ≈ 1 000 km
Indus:
2 847 km ≈ 3 000 km
Wolga:
3 685 km ≈ 4 000 km
Amazonas
Elbe
Indus
Wolga
0
1000
5000
km
41
Darstellung von Zahlen in Diagrammen
1
Runde und fertige ein Diagramm für alle Daten an.
970 000 000 Menschen sprechen Mandarin (China), 456 000 000 Menschen
­sprechen Englisch, 383 000 000 Menschen Hindi (Indien), 362 000 000 Menschen
Spanisch, 293 000 000 Menschen sprechen Russisch und 208 000 000 Menschen
Arabisch. Trage auch ein, dass im Vergleich dazu 119 000 000 Menschen Deutsch
sprechen.
2
Betrachte das Diagramm. Entscheide, ob alle Aussagen durch das Diagramm belegt werden.
wahr
falsch
??
a) Insgesamt wurden 110
Arbeitnehmer befragt.



b) Weniger als 10 Arbeitnehmer
wohnen höchstens 500 m weit
von der Arbeitsstelle entfernt.



c) Mehr als die Hälfte der
Arbeitnehmer wohnt weiter als
2,5 km von der Arbeitsstelle
entfernt.



d) Mehr als 25 Arbeitnehmer
kommen mit dem Fahrrad.



e) Weniger als _​ 3 ​der Arbeitnehmer wohnt weiter als 4 km von
der Arbeitsstelle entfernt.



f) Mindestens 40 Arbeitnehmer wohnen in einer Entfernung zwischen 2,5 km und 7 km.



g) 5 Arbeitnehmer wohnen
weiter als 7 km entfernt.






1
3
h)​ _4 ​aller Arbeitnehmer wohnen außerhalb eines Radius
von 1 km.
42
Anzahl
Arbeitnehmer
0
10
über 7 km
4 – 7 km
20
30
2,5 – 4 km
1 bis 2,5 km
40
0 bis 1 km
Dreisatz mit geradem/proportionalem Verhältnis
Beispiel
Gilt für ein Verhältnis von zwei Größen:
„je mehr – desto mehr“ oder „je weniger –
desto weniger, so nennt man dies ein
gerades Verhältnis oder proportionales Verhältnis.
3 Kiwis kosten 1,20 €. Wie viel kosten 5 Kiwis?
Preis:
Zuordnung Stück
1. 3 Kiwis kosten 1, 20 €
2. 1 Kiwi kostet 0,40 €
3. 5 Kiwis kosten 2,00 €
Die gesuchte Größe kann mit dem Dreisatz
berechnet werden.
1. Schritt: Zuordnung in eine Tabelle eintragen
2. Schritt: Anteil „1“ ausrechnen
3. Schritt: gewünschte Menge ausrechnen
ja
Benzinmenge in Liter
Preis pro Liter in €
x
Geldwert in €
Geldwert in Britische Pfund
x
x
Gewicht eines Briefes
Portogebühr in €
x
kW-Wert eines Autos
Geschwindigkeit des Autos
2
5 m Stoff kosten 80 €. Wie
viel kosten 3 m vom gleichen
Stoff?
:5
·3
Länge
5m
1m
3m
Preis
80 €
16 €
48 €
:5
·7
Stück
5
1
7
Preis
20 €
4€
28 €
3
Aus einem Wasserhahn
strömen 8 ø Wasser in 24 Sekunden aus. Wie lange dauert es, bis
ein 15-ø-Eimer gefüllt ist?
:8
·3
· 15
5 Knäuel Wolle kosten 20 €.
Für einen Pullover werden
7 Knäuel gebraucht. Wie viel
kostet die Wolle für den Pullover?
1,20
0,40
2,00
·5
:3
·5
x
:5
5
3
1
5
:3
Zuordnungsaufgaben können auf unterschiedliche
Arten gelöst werden. Notiere hier, wie du die Lösung
der Beispielaufgabe gelernt hast.
nein
Alter eines Menschen in Jahren
Körpergröße in cm
Preis
in €
Auf beiden Seiten wird entweder
malgenommen oder geteilt!
1 Entscheide, welche Zuordnungen ein gerades
Verhältnis haben.
Gerades Verhältnis?
Stück
Füllmenge
8ø
1ø
15 ø
6
Zeit
24 s
3s
45 s
: 10
· 15
· 25
2
:5
: 12
·7
·5
2
12 m
2
1m
2
5m
Anzahl
Fliesen
540
45
225
Für 10 Euro bekommt man
13 US-Dollar. Wie viel US-Dollar
bekommt man für 25 €?
:8
Für 12 m Wandfläche werden 540 Fliesen gebraucht. Wie
2
viele Fliesen werden für 5 m
benötigt?
Fläche
4
Euro
10
1
25
Dollar
13
1,3
32,50
: 10
· 25
7 20 Bonbons wiegen 160 g.
Wie viel wiegen 7 Bonbons?
: 12
: 20
·5
·7
Anzahl
Bonbons
20
1
7
Gewicht
160
8
56
: 20
·7
43
Dreisatz mit ungeradem/umgekehrt proportionalem Verhältnis
z
Gilt für ein Verhältnis von zwei Größen: „je mehr
– desto weniger“ oder „je weniger – desto mehr“,
so nennt man dies ein ungerades Verhältnis
oder umgekehrt proportionales Verhältnis.
Auch hier kann die gesuchte Größe mit dem
Dreisatz berechnet werden.
Beispiel
4 Arbeiter schaffen einen Umzug in 3 Stunden.
Wie viele Stunden brauchen 6 Arbeiter?
Zuordnung Arbeiter
Zeit:
1. 4 Arbeiter brauchen 3 h
2. 1 Arbeiter braucht 12 h
3. 6 Arbeiter brauchen 2 h
1. Schritt: Zuordnung in eine Tabelle eintragen
2. Schritt: Anteil „1“ ausrechnen
3. Schritt: gewünschte Menge ausrechnen
ja
Größe eines Kekses
Kekse aus einem Teig
Anzahl der
Größe eines Glases
mögen eines Glases
Fassungsver-
Brenndauer einer Kerze
einer Kerze
Geldbetrag
Münzen
t
Zeit
4
1
6
3
12
2
:4
·6
·4
:6
Wird auf der einen Seite malgenommen,
dann wird auf der anderen Seite geteilt!
1 Entscheide, welche Zuordnungen ein
ungerades Verhältnis haben.
Ungerades Verhältnis?
Anzahl
Arbeiter
Notiere hier, wie du die Lösung der
Beispielaufgabe gelernt hast:
nein
x
x
Länge
x
Anzahl der benötigen
x
2 Ein Lottogewinn von 120 000 € soll auf eine Tippgemeinschaft aufgeteilt werden. Wie viel Euro erhält
jedes Mitglied der Tippgemeinschaft bei der angegebenen Gruppengröße?
Anzahl der
Personen
Gewinn
(in €)
1
2
3
4
5
6
8
120 000
60 000
40 000
30 000
24 000
20 000
15 000
3 2 Maler brauchen für das
Streichen eines Schulgebäudes
12 Arbeitstage. Wie lange brauchen
3 Maler?
8 Tage
44
4 Ein Florist bindet
8 Sträuße mit jeweils 15 Tulpen.
Wie viele Sträuße kann er binden, wenn nur 10 Tulpen in
einem Strauß sind?
12 Sträuße
5 Der Futtervorrat reicht bei
12 Kühen für 28 Tage. Wie lange
reicht er bei 7 Kühen?
48 Tage
Gerader und ungerader Dreisatz
1 Lassen sich die Aufgaben mit dem Dreisatz lösen? Kreuze die Aufgaben an, bei denen eine Lösung mit
dem Dreisatz möglich ist. Berechne danach für zwei der Aufgaben die Lösungen.
a) Eike ist 16 Jahre alt und
1,74 m groß. Seine Schwester
ist 19 Jahre alt. Wie groß ist sie?
ssen 150 g
b) In eine Tasse pa
m sind es,
Reis. Wie viel Gram _1 ssen
e 2 Ta
wenn mit der Tass 2
werden?
n
se
Reis abgemes
papier ergec) 500 Blatt Kopier
hen Papierben einen 5 cm ho
elen Blättern
stapel. Aus wie vi
, der 3,5 cm
besteht ein Stapel
hoch ist?
Individuelle
Lösung
d) Ein Freibadbec
ken wird mit
Wasser befüllt. Na
ch 4 Stunden
sind 80 000 Liter W
asser im
Becken. Wie viel Li
ter sind es
nach 5 Stunden?
e) Ein Langstreck
enläufer benötigt
für 3 000 m etwa 9
Wie lange brauch
Minuten.
t er für 10 000 m?
2
Handelt es sich bei den Aufgaben um gerade oder ungerade Verhältnisse? Berechne die Lösung.
a) Aus 9 kg Hartweizen werden
3 000 Spaghetti hergestellt.
Wie viel Hartweizen braucht man
für 4 000 Spaghetti?
gerade
 ungerade
Antwort: 12
:3
·4
3
Kg
9
3
12
c) Die Spaghetti-Fabrik produziert
560 Packungen mit je 250 g Inhalt.
Wie viele Packungen mit 1 kg können stattdessen hergestellt
werden?
 gerade
 gerade
ungerade
Antwort: 1 800
kg
Stück
3 000
1 000
4 000
b) Die 3 000 produzierten
Spaghetti haben eine Länge von
30 cm. Wie viele 50 cm lange
Spaghetti können produziert
werden?
:3
·3
·4
:5
Stück
3 000
9 000
1 800
Stück
Länge
30
10
50
:3
:4
Pck.
560
140
Pakete
Inhalt
250 g
1 000 g
·4
Malermeister Kuhn sagt: „Mit 2 Litern Farbe können 10 m2 Wandfläche gestrichen werden.“
m2
Antwort: 25
·5
Antwort: 140
·5
a) In einem Farbeimer sind 5 Liter b) Wie viel Liter Farbe benötigt
Wandfarbe. Welche Fläche kann
man für eine Fläche von 35 m2?
damit gestrichen werden?
:2
ungerade
ø
2
1
5
m2
10
5
25
Antwort: 7
:2
: 10
·5
· 35
ø
2
0,2
7
Antwort: nein
ø
m2
10
1
35
c) Von einem 10-Liter-Eimer sind
bereits 6 Liter verbraucht. Reicht die
Farbe noch für die restlichen 25 m2?
: 10
:2
· 35
·4
ø
2
1
4
m2
10
5
20
:2
·4
45
Dreisatz mit geradem und ungeradem Verhältnis
1 Ein Arbeitnehmer verdient in 7 Stunden
63,00 €. Wie viel verdient er in einem Monat mit
21 Arbeitstagen und einer täglichen Arbeitszeit
von 8 Stunden?
21 · 8 = 168
: 7
· 168
Stunden
7
1
168
€
63
9
1512
: 7
z
Lösen von Textaufgaben mit dem Dreisatz:
1. Schritt: Zuordnung notieren
2. Schritt:Welche Zuordnung liegt vor: ein gerades oder ein ungerades Verhältnis?
3. Schritt:Berechnen
4. Schritt:Antwort notieren
· 168
Antwort: Er verdient 1 512 ¤.
2 Eine Reisegruppe kommt mit 4 vollbesetzten
Bussen mit jeweils 48 Sitzplätzen in einen Safaripark.
Dort muss sie in Busse mit 12 Sitzplätzen umsteigen.
Wie viele Busse muss der Reiseveranstalter
bereitstellen?
· 4
Busse
4
16
Plätze
48
12
· 22
4
Um ein Brückengeländer zu streichen, benötigen 9 Arbeiter 16 Tage. Vor Beginn der Arbeit wird
eine Person krank und fällt aus. Um wie viele Tage
verzögert sich die Arbeit?
: 9
· 8
Tage
16
144
18
· 9
: 8
Antwort: Die Arbeit verzögert sich um 2 Tage.
h
: 3
: 4
Antwort: Er muss 16 Busse bereitstellen.
Arbeiter
9
1
8
3 Der Computer-Raum einer Schule muss mit
optischen Mäusen ausgestattet werden. Drei Stück
gibt es schon, diese kosteten 50,85 €. Insgesamt werden 22 Stück benötigt.
Stück
3
1
22
€
50,85
16,95
372,90
: 3
· 22
Gesamtkosten: 372,90 €
5
Familie Meier zahlt für ihre 70 ​m2​​ ​-Wohnung
315 € Miete. Wie viel zahlen die Nachbarn bei gleichem Quadratmeterpreis für ihre 88 m​​​2​-Wohnung?
: 70
· 88
​ 2​ ​
m
70
1
88
€
315
4,5
396
: 70
· 88
Antwort: Die Nachbarn müssen 396 € bezahlen.
6
Zwei Zahnräder mit unterschiedlicher Anzahl an Zähnen greifen ineinander.
Das kleine Zahnrad hat 24 Zähne, das große hat 68 Zähne.
a) Das kleine Zahnrad dreht sich in einer Minute 17-mal. Wie oft dreht sich das große Zahnrad?
SE84746371_G_K03_067_02.eps
Antwort: Das große Zahnrad dreht sich 6-mal.
b) Wie viele Zähne müsste das Zahnrad haben, wenn es sich nur 4-mal drehen soll?
Antwort: Das Zahnrad müsste 102 Zähne haben.
46
Test: Dreisatz
1
Berechne mit dem Dreisatz.
10 kg Kartoffeln kosten 3,50 €.
Wie viel Euro kosten 30 kg?
10,50 €
10 kg Äpfel kosten 14 Euro.
Wie viel kosten 7 kg?

9,80 € 1 kg Aufschnitt kostet 9,80 €.
Wie viel kosten 450 g Aufschnitt?

4,41 €

5 LKWs fahren einen Schuttberg
in 12 Tagen ab. Wie viele Tage
benötigen 6 LKWs?
Eine Busfahrt kostet bei 21 Schülern für jeden Schüler 24,00 €.
Wie viel Euro muss jeder bezahlen, wenn nur 20 Schüler
mitfahren?
Die Vorräte im Basislager reichen
12 Bergsteigern 36 Tage. Wie viele
Tage können 18 Bergsteiger von
den Vorräten leben?
10 Tage
25,20 €
24 Tage

Aus einem Rohr laufen in 15
Minuten 3 600 Liter Öl. Wie viel
Liter laufen in 25 Minuten aus
dem Rohr?
6 000 Liter
Bronze:

Silber:


In einer Abfüllanlage werden in
1
1 ​ _2 ​Minuten 45 ø Fruchtsaft abgefüllt. Wie viel Liter Fruchtsaft werden in 7 Minuten abgefüllt?
Ein Gewinn wird an 12 Personen
verteilt, jede Person erhält
5 928 €. Wie viel Euro erhält jeder
bei einer Verteilung an 13
Personen?
210 Liter
5 472 €
Gold:


(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 77.)
47
z
Prozentrechnen: Grundbegriffe
Beim Prozentrechnen werden die folgenden Begriffe verwendet:
Prozentsatz
50%
30%
20% ➔ der Anteil vom Ganzen in Prozent (kurz: p %)
Prozentwert
150 €
90 €
60 € ➔ der Anteil vom Ganzen in der Einheit (kurz: W)
➔ das Ganze (kurz: G)
300 €
Grundwert
Der Grundwert entspricht immer 100 %.
1 Bestimme in den folgenden Aufgaben den Prozentsatz (p %), den Prozentwert (W) und den
Grundwert (G).
von 30 Schülern G
b) 6 W
o in die
einer Klasse kommen mit dem Aut
.
p%
%
20
au
gen
Schule. Das entspricht
a) Von 20 Aufgaben G
wurden 80 %
p%
richtig gelöst. Das sind genau
16 Aufgaben W
.
ihrer gesparten 200 €
d) 25 % p %
hat Susanne ausgegeben, nämG
.
lich genau 50 € W
G
c) Von den angelieferten 60 Handys
wurden 24 Handys W
– sofort verkauft.
– also 40 % p %
e) Die Stiftung Warentest hat insgesamt 658 Tests G
bei Weintrauben
durchgeführt. Bei 15 Prozent p %
der Proben und damit in 100 Fällen
W
wurden zu viele Schadstoffe gefunden.
2
Was soll hier berechnet werden? Kreuze an.
Prozentsatz
a) 20 % von 3 000 t.

b) 12,5 % sind 80 €.

Prozentwert


c) 45 kg von 360 kg.

d) 40 % sind 1 500 Stück.
Grundwert



3 Lies den nebenstehenden Text genau durch. Ermittle danach die genauen Anzahlen der Schülerinnen
und Schüler. Entscheide bei jeder berechneten Zahl, ob es sich um den Grundwert, Prozentwert oder Prozentsatz handelt.
a) Gesammtzahl der befragten Personen: 960
Grundwert
Prozentwert
Prozentsatz
b) Beleidigungen oder Bedrohungen: 480
Grundwert
Prozentwert
Prozentsatz
c) Bedrohung: 25 %
Grundwert
48
Prozentwert
Zum Thema „Mobbing“ wurden 960 Schülerinnen und
Schüler befragt. 480 davon sind beleidigt oder bedroht
worden. 40 Prozent waren Ziel von massiven verbalen Angriffen, 25 Prozent Opfer einer Bedrohung.
Eine andere Befragung ergab, dass 10 Prozent gelegentlich
unter Kopf- oder Bauchschmerzen bei Klassenarbeiten leiden.
d) Kopf- und Bauchschmerzen: 10 %
Prozentsatz
Grundwert
Prozentwert
Prozentsatz
Prozentwert berechnen
z
Beispiel
Wie viel sind 60 % von 250 Metern?
1. Schritt: gegebene Werte bestimmen
2. Schritt: gegebene Werte in die Prozentformel
einsetzen
3. Schritt: Prozentwert berechnen
4. Schritt: Antwort notieren
1
2¤
b) 4 % von 200 kg =
8 kg
c) 80 % von 200 ¤ =
160 ¤
p % = 60 %
also p = 60
2.
3.
mit Dezimalzahlen:
250 m · 60 : 100
= 250 m · 0,6 = 150 m
p
W = G · ___
100
100
mit Brüchen:
60 3
250 · ___
100 = 150 m
5
Antwort: 60 % von 250 m sind 150 m.
Du kannst den
Prozentwert auch
mit dem Dreisatz
berechnen:
: 100
250 m = 100 %
2,5 m = 1 %
· 60
150 m = 60 %
12 km
b) 25 % von 220 kg =
55 kg
c) 70 % von 920 cm =
25
24
· 60
644 cm
70
50 · ___
100 = 12
220 · ___
100 = 55
920 · ___
100 = 644
(Rechenbeispiel)
(Rechenbeispiel)
(Rechenbeispiel)
3
: 100
Bestimme den Prozentwert W. Notiere deinen Lösungsweg.
a) 24 % von 50 km =
t
G = 250 m
60
250 m · ___
4.
Bestimme den Prozentwert im Kopf.
a) 1 % von 200 € =
2
1.
Bestimme den Prozentwert W.
a) 45 % von 320 m =
144 m
b) 85 % von 180 ø =
c) 30 % von 330 g =
99 g
d) 125 % von 321 m = 401,25 m
e) 130 % von 1 700 € =
2 210 €
f) 20 % von 70 ø =
14 ø
g) 15 % von 250 € =
37,5 €
h) 2 % von 420 t =
8,4 t = 8 400 kg
4 Kartoffeln bestehen zu 76 %
aus Wasser. Wie viel Gramm Wasser
sind in 750 kg Kartoffeln enthalten?
153 ø
76
750 · ___
100 = 570
(Rechenbeispiel)
G=
750 g
p% =
76 %
Antwort: Es sind 570 g Wasser enthalten.
5
Eine Kücheneinrichtung kostet 6 000 €.
Bei Barzahlung bekommt Herr Krause 3 % des Kaufpreises abgezogen. Wie viel zahlt er weniger?
G=
6 000 €
p% =
3%
3
6 000 · ___
100 = 180
(Rechenbeispiel)
Antwort: Herr Krause zahlt 180,00 € weniger
49
Prozentsatz berechnen
z
Beispiel
Beispiel: Wie viel Prozent sind 25 von 250 Schülern?
1. Schritt: gegebene Werte bestimmen
2. Schritt: gegebene Werte in die Prozentformel
einsetzen
3. Schritt: Prozentsatz p % berechnen
4. Schritt: Antwort notieren
Berechnung mit
dem Dreisatz:
250 Schüler = 100 %
: 250
· 25
1
G = 250
2.
100·25
p = _____
3.
mit Dezimalzahlen:
p = 100 · 25 : 250
= 2 500 : 250
= 10
: 250
1 Schüler = 0,4 %
W = 25
100·W
p = ______
G
250
mit Brüchen:
100 · 25 1 ___
100 10
p = _____
250 = 10 1= 10
10
p = 10 also p % = 10 %
· 25
25 Schüler = 10 %
4.
25 von 250 Schülern sind 10 %.
Bestimme den Prozentsatz p %. Notiere deinen Lösungsweg.
a) 15 cm von 60 cm
b) 36 kg von 80 kg
c) 36 cm von 48 cm
100 · 15
_____
= 25
100 · 36
_____
= 45
100 · 36
_____
= 75
(Rechenbeispiel)
(Rechenbeispiel)
(Rechenbeispiel)
80
60
p% =
t
1.
2
25 %
p% =
48
45 %
75 %
p% =
Bestimme den Prozentsatz p % .
a) 15 m von 20 m
p% =
75 %
b) 360 ø von 400 ø
p% =
90 %
c) 17 € von 85 €
p% =
20 %
d) 84 kg von 150 kg
p% =
56 %
e) 13 m von 55 m
p% =
24 %
f) 4 km von 44 km
p% =
9%
g) 13 kg von 65 kg
p% =
20 %
h) 90 cm von 125 cm
p% =
72 %
3 Bei einer Radarkontrolle von 350 Autos fuhren 42 Autos zu schnell.
Wie viel Prozent der Autos fuhren zu schnell?
G=
350 Autos
P=
100 · 42
_____
= 12
42 Autos
350
(Rechenbeispiel)
Antwort: Es fuhren 12 % aller Autos zu schnell.
4
Herr Schulte hat 1 500 € auf seinem Konto. Am Jahresende
bekommt er 60 € Zinsen. Wie viel Prozent Zinsen hat er bekommen?
100 · 60
_____
=4
1 500
G=
1 500 €
P=
60 €
(Rechenbeispiel)
Antwort: Herr Schulte hat 4 % Zinsen bekommen.
t
5 In 500 g weißen Bohnen sind 10 g Fett, 105 g
Eiweiß und 285 g Kohlenhydrate enthalten.
Berechne den jeweiligen Prozentsatz und trage
das Ergebnis in die Tabelle ein.
50
500 g
Bohnen
enthalten
Fett
Eiweiß
Kohlehydrate
2%
21 %
57 %
Grundwert berechnen
z
Beispiel
Eine Jeans wurde um 25 % reduziert. Das sind 15 €.
1. Schritt: gegebene Werte bestimmen
2. Schritt: gegebene Werte in die Prozentformel
einsetzen
3. Schritt: Grundwert G berechnen
4. Schritt: Antwort notieren
Berechnung mit
dem Dreisatz:
25 % = 15 €
: 25
· 100
100 % = 60 €
20
300 €
G=
4
100·15
G = ____
25 = 60
1
100 · 72
_____
= 480
(Rechenbeispiel)
(Rechenbeispiel)
15
60 kg
100 · 150
_____
= 500
(Rechenbeispiel)
27
(Rechenbeispiel)
300 €
(Rechenbeispiel)
500 cm
G=
e) 27 % von G sind 108 m.
100 · 108
_____
= 400
30
16
480 m
G=
d) 30 % von G sind 150 cm.
100 · 48
_____
= 300
c) 15 % von G sind 72 m.
100 · 36
_____
= 60
G=
c) 16 % von G sind 48 €.
t
mit Brüchen:
Die Jeans kostete vorher 60 €.
60
(Rechenbeispiel)
2
3.
mit Dezimalzahlen:
G = 100 ·15 : 25
= 1 500 : 25
= 60
4.
100 · W
G = _______
p
100·15
G = ____
25
b) 60 % von G sind 36 kg.
100 · 60
_____
= 300
t
p % = 25 %
also p = 25
Bestimme den Grundwert G.
a) 20 % von G sind 60 €.
G=
W = 15 €
2.
1 % = 0,6 €
· 60
1
: 25
1.
G=
400 m
Bestimme den Grundwert G.
a) 10 % von G sind 69 m
G=
690 m
b) 40 % von G sind 60 €
G=
150 €
c) 40 % von G sind 24 l
G=
60 ø
d) 25 % von G sind 4 kg
G=
16 kg
e) 9 % von G sind 117 km
G=
1 300 km
f) 2 % sind 26 m
G=
1 300 m
g) 5 % von G sind 37,50 €
G=
750 €
h) 8 % von G sind 92,80 €
G=
1 160 €
3 Für die Autohaftpflicht zahlt Frau Pflug 450 €. Das sind 60%
der vollen Prämie. Wie viel Euro beträgt die volle Prämie?
Gegebene Werte: P = 450 €, p % = 60 %
Antwort: Die volle Prämie beträgt 750 €.
51
Verminderter oder vermehrter Grundwert
Beim Prozentrechnen ist es wichtig zu beachten, ob der Prozentwert vom Grundwert
abgezogen wird oder ob der Prozentwert zum Grundwert hinzugezählt wird.
Beispiel: Verminderter Grundwert
Beispiel: Vermehrter Grundwert
Im Sommerschlussverkauf wird ein Pullover für 40 €
um 10 % reduziert.
Eine Monatskarte für den Bus kostet 40 €. Zum neuen
Jahr erhöhen die Verkehrsbetriebe den Preis um 10 %.
➔ Vom Grundwert werden 10 % abgezogen.
➔ Zum Grundwert werden 10 % hinzugezählt.
Neuer Prozentsatz: 100 % – 10 % = 90 %
Neuer Prozentsatz: 100 % + 10 % = 110 %
90
Rechnung: 90 % von 40 €: 40 · __
100 = 36 €
110
Rechnung: 110 % von 40 €: 40 · __
100 = 44 €
Antwort: Der Pullover kostet nun 36 €.
Antwort: Die Fahrkarte kostet nun 44 €.
+ 10 %
– 10 %
40 €
100 %
t
1
40 €
100 %
36 €
90 %
44 €
110 %
Bestimme den neuen Grundwert.
a)
b)
c)
d)
Anfangswert
700 €
500 €
420 €
325 €
Veränderung
+3%
–7%
– 11 %
+ 15 %
Neuer Prozentsatz
103 %
93 %
89 %
115 %
721
465
373,8
373,75
Ergebnis
2
Laut Katalog soll ein Computer komplett 980 € kosten. Es kommen noch 19 % dieses Preises als Mehrwertsteuer hinzu. 2 % des Gesamtpreises können bei Barzahlung wieder abgezogen werden.
a) Berechne den Endpreis
bei Kartenzahlung.
980 € · 1,19
= 1 166,20 €
b) Berechne den Endpreis
bei Barzahlung.
11 66,20 € · 0,98
= 1 142,88
3
Nach einer Mieterhöhung um 3,5 % zahlt Familie Müller 724,50 € Miete.
Wie viel hat die Familie vor der Mieterhöhung bezahlt?
Antwort: Familie Müller hat vor der Erhöhung 700 € Miete bezahlt.
52
Textaufgaben: Grundwert, Prozentwert und Prozentsatz
1
Ein Mountainbike kostet 480 €. Im Sonderverkauf zahlt man nur 75 %.
Gegebene Werte: G = 480 €, p %= 75 %
Formel:
Prozentrechnung:
Gesuchter Wert: W
W
p
G·p
W = ____
100
Rechnung:
W = 480 · (75 : 100) = 360
G
G·p
= ____
100
100
·__
W
___
=
G
100 ·__
W
= ___
p
Antwortsatz: Das Fahrrad kostet im Sonderverkauf 360,00 €.
2 Beim Kauf seines Autos macht Herr Seifer eine Anzahlung von 4 500 €. Das sind 25 % des Kaufpreises.
Wie viel kostet das Auto insgesamt?
Gegebene Werte: W = 4 500 €, p % = 25 %
Formel:
Gesuchter Wert: G
100 · W
G = _____
p
Rechnung:
G = (100 · 4 500) : 25 = 18 000
Antwortsatz: Das Auto kostet insgesamt 18 000 €.
3
Im Astoria-Kino kostet die Eintrittskarte normalerweise 4 €. Wegen Überlänge des Films wird ein
Zuschlag von 25% erhoben. Wie viel Euro kostet der Eintritt bei Überlänge?
Gegebene Werte: G = 4 €, p % = 125 %
Formel:
Gesuchter Wert: W
G·p
W = ___
100
Rechnung:
W = (4 · 125) : 100 = 5
Antwortsatz: Der Eintritt kostet bei Überlänge 5 €.
t
4 Ulrike sucht sich in der Secondhand-Buchhandlung LESEBAR zwei Taschenbücher für je 3,95 €, je eines für 6,95 € bzw. 7,95 € und eines für 13,00 € aus.
35,80 €
a) Was bezahlt Ulrike ohne Rabatt?
b) Mit dem Rabatt muss sie nur noch
t
30,43 €
bezahlen.
5
Ein Händler hat zu Ferienbeginn alle Preise um 10 % reduziert. Zu Schuljahresbeginn werden die Preise
um 10 % erhöht. Gelten jetzt die alten Preise?
– 10 %
24 €
+ 10 %
21,60
Alter Preis?
23,76
ja
nein
– 10 %
50,00 €
+ 10 %
45,00
Alter Preis?
49,50
ja
nein
53
Textaufgaben: Brutto, Netto, Tara
1 Frau Burger erhält einen Bruttolohn von 3 100 €.
Berechne die Abgaben und den Nettolohn.
Bruttolohn
3 100,00 €
Lohnsteuer:
11 % des Bruttolohns
341,00 €
Solidaritätszuschlag:
5,5 % der Lohnsteuer
18,76 €
Bruttolohn: gesamter Lohn
Abzüge:
Steuer und Abgaben, z.B. Lohnsteu
er,
Arbeitslosenversicherung, Krankenversicherung, Kirchensteuer
Nettolohn: Lohn nach allen Abzü
gen
Bruttolohn
Nettolohn
Kirchensteuer:
8 % der Lohnsteuer
27,28 €
Krankenversicherung:
15,5 % des Bruttolohns
480,50 €
Rentenversicherung:
9,75 % des Bruttolohns
302,25 €
Arbeitslosenversicherung:
3,25 % des Bruttolohns
100,75 €
Pflegeversicherung:
0,85 % des Bruttolohns
26,35 €
Nettolohn
1 803,11 €
2
Lohn und Gehalt
Abzüge
Frau Stahl hat ihre Lohnabrechnung erhalten.
a) Wie viel Prozent ihres Bruttolohns bekommt Frau
Stahl ausbezahlt? Runde sinnvoll.
Rechnung:
p = 100 · 1 147,21 : 1 705,6 = 67,26
Antwort: Frau Stahl bekommt 67 % ausbezahlt.
t
t
b) Die Höhe der Kirchensteuer ist in den Bundesländern unterschiedlich.
Manche verlangen 8 %, andere 9 % von der Lohnsteuer.
Welcher Prozentsatz ist es bei Frau Stahl?
8 %
9 %
c) Berechne die Prozentsätze der einzelnen Sozialversicherungen. Bedenke, dass die Sozialversicherungen
vom Bruttolohn ausgehend berechnet werden.
Rentenversicherung:
9,75
%
Krankenversicherung:
6,7
%
Arbeitslosenversicherung:
3,25
%
Pflegeversicherung:
0,85
%
3 Das Bruttogewicht einer Kiste mit Kartoffeln beträgt
94 Kilo. Die Verpackung wiegt 14,1 kg.
a) Wie viel Prozent des Gewichts macht
die Verpackung aus?
b) Wie groß ist das Nettogewicht?
c) Wie viel Prozent vom Bruttogewicht
ist das Nettogewicht?
54
15
%
79,9
kg
85
%
Gewicht
Bruttogewicht: Gesamtgewicht
Tara: Gewicht der Verpackung
Nettogewicht: Gewicht ohne Verpacku
ng
Bruttogewicht
Nettogewicht
Tara
Test: Prozente
1
Berechne den Prozentwert W.
75 % von 120 ø = 90 ø
2
39 % von 250 kg = 97,5 kg

16 € von 80 € = 20 %


8 € von 125 € = 6,4 %


Berechne den Grundwert G.
20 % von G sind 30 cm.
150 cm
4

Berechne den Prozentsatz p%.
88 € von 400 € = 22 %
3
83 % von 82,4 cm = 68,39 cm
62 % von G sind 80 €.
129,03 €

15 % von G sind 125 €.
833,33 €


Berechne den fehlenden Wert.
Anfangswert: 550 €
Veränderung: + 6 %
Ergebnis: 583,00 €
Anfangswert: 345 kg
Veränderung: – 11 %
Ergebnis: 307,05 kg
Anfangswert: 36,40 €
Veränderung: – 32,5 %
Ergebnis: 24,57 €



Das Holz für ein Regalsystem
kostet 650 €. Für das Zuschneiden
wird ein Zuschlag von 20 % erhoben. Wie viel Euro sind zu zahlen?
In einer Regentonne sind 91 Liter.
Damit ist sie 65 % gefüllt. Wie
groß ist das Fassungsvermögen
der Regentonne?
Auf den Netto-Rechnungsbetrag
einer Stromrechnung von
1 600 € werden 19 % Mehrwertsteuer aufgeschlagen. Der
Stromanbieter gewährt bei Einzug vom Konto 3 % Rabatt.
Berechne den Gesamtpreis.
780 €
140 Liter
1 846,88 €
5
Bronze:

Silber:
Gold:


(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 78.)
55
z
Zinsrechnen - Grundbegriffe
Zinsen:
Die Zinsrechnung ist die Anwendung der Prozentrechnung bei
Geldgeschäften.
Prozentrechnung
Grundwert
G
Prozentsatz
p%
Prozentwert
W
Zinsrechnung
Kapital
K
Zinssatz
p%
Jahreszinsen
Z
Habenzinsen erhält man für Guthaben auf Konten.
Sollzinsen muss man für Darlehen
oder Kredite bezahlen.
1 Bestimme Kapital, Zinssatz und Jahreszinsen.
a) Jenny hat auf ihrem Sparbuch 600 €. Das Geld wird zu 6 % verzinst. Sie erhält nach einem Jahr 36 €
Jahreszinsen.
Kapital:
K = 600 €
Zinssatz:
p% = 6%
Jahreszinsen:
Z = 36 €
b) Bei der Bank kann man Sparbriefe kaufen. Sie erbringen im Jahr 7 % Zinsen. Nach einem Jahr bekommt
man 350 € für 5 000 € ausbezahlt.
Kapital:
K = 5 000 €
Zinssatz:
p% = 7%
Jahreszinsen:
Z = 350 €
c) Frau Kapell will ein Auto kaufen. Sie nimmt bei der Bank ein Darlehen über 15 000 € auf. Sie muss 1 200 €
Jahreszinsen zahlen. Das sind 8 %.
Kapital:
K = 15 000
Zinssatz:
p% = 8%
Jahreszinsen:
Z = 1 200 €
d) Frau Schröder hat 600 000 € geerbt. Wenn sie diese zu 8 % anlegen kann, erhält sie jährlich 48 000 €.
Kapital:
K = 600 000 €
Zinssatz:
p% = 8%
Jahreszinsen:
Z = 48 000
e) Herr Masch hat 9 000 € zu 9% an einen Freund verliehen. Nach einem Jahr bekommt er 9 810 € zurück.
Kapital:
K = 9 000
Zinssatz:
p% = 9%
Jahreszinsen:
Z = 810
f) Frau Brehm träumt: Sie möchte so viel Geld gewinnen, dass sie jeden Monat 3 000 € aus Zinsen zu Verfügung hätte. Das wären 36 000 € im Jahr. Bei einem Zinssatz von 6 % müsste sie 600 000 € gewinnen.
Kapital:
2
K = 600 000
Zinssatz:
p% = 6%
Z = 36 000
Was soll hier berechnet werden? Kreuze an.
Zinssatz
a) 2,5 % von 3 000 €.

b) 8 % sind 80 €.

d) 40 % sind 500 €.


Kapital





e) 45 € von 350 €.
f) 7 % von 350 €.
Jahreszinsen

c) 60 Euro von 800 €.
56
Jahreszinsen:


Jahreszinsen berechnen
z
1. Schritt: gegebene Werte bestimmen
2. Schritt: gegebene Werte in die Zinsformel
einsetzen
3. Schritt: Jahreszinsen Z berechnen
4. Schritt: Antwort notieren
Beispiel
Wie viel Jahreszinsen erhält man bei einem Kapital
von 600 € bei einer Verzinsung von 7 %?
1. K = 600 €
p% = 7%
also p = 7
7
2. 600 € · ___
100
p
Z = K · ___
100
3. 600 € · 0,07 = 42 €
4. Man erhält 42 € Jahreszinsen.
1
Für ein Darlehen von 3 500 € muss Frau Schulz
12 % vom Kapital zahlen. Wie viel Euro sind das?
Gegebene Werte: K = 9 000 €, p % = 4 %
Gegebene Werte: K = 3 500 €, p % = 12 %
Rechnung:
4
9 000 € · ___
100 = 360 €
Rechnung:
12
3 500 € · ___
100 = 420 €
Antwort: Er erhält 360 € Jahreszinsen.
Antwort: Sie muss 420 € Zinsen bezahlen.
3 Ein Sparguthaben von 3 400 € wird mit 3 % verzinst. Berechne die Jahreszinsen.
4 Zum Autokauf fehlen 11 000 €. Es wird ein Kredit zu 6,2 % gewährt. Berechne die Jahreszinsen.
Gegebene Werte: K = 3 400 €, p % = 3 %
Gegebene Werte: K = 11 000 €, p % = 6,2 %
Rechnung:
3
3 400 € · ___
100 = 102 €
Rechnung:
Antwort: Die Jahreszinsen betragen 102 €.
t
2
Herr Schmidt hat 9 000 € in Sparbriefen angelegt. Der Zinssatz beträgt 4 % . Wie viel Euro Zinsen
erhält er nach einem Jahr?
5
11 000 € · 0,062 = 682 €
Antwort: Die Jahreszinsen betragen 682 €.
Berechne die Jahreszinsen und trage das Ergebnis ein.
Kapital K
2 250 €
343 €
19 250
21 540 €
Zinssatz p%
11 %
4%
16 %
12 %
Jahreszinsen Z
247,50 €
13,72 €
3 080 €
2 584,80 €
6
Welches Kreditangebot ist günstiger? Kreuze an.
Sofortkredit:
Barkredit:
9
Jahreszinsen: 2 000 € · ___
100 = 180 €
Gesamtkosten = Jahreszins + Bearbeitungsgebühr
180 € + 25 € = 205 €
Sofortkredit!
2 000 €
Zinssatz: 9 %; Bearbeitung 25,00 €
Rückzahlung nach einem Jahr
9,5
Jahreszinsen: 2 000 € · ___
100 = 190 €
2 000 € Barkredit!
Zinssatz: 9,5 %;
keine Bearbeitungsgebühr!
Rückzahlung nach einem Jahr
57
Senkrechte und parallele Linien
z
Die Linien g und h verlaufen senkrecht.
Der Winkel zwischen den Geraden ist ein rechter
Winkel ¾
Die Linien a und b sind immer gleich weit
voneinander entfernt. Dann verlaufen sie
parallel.
1
Parallele Linien (Parallelen) mit dem
Geodreieck zeichnen:
Welche Geraden sind senkrecht zu h?
f
e
d
c
b
a
7
6
10 0
17
5
20
160
4
2
40
140
70
110
8
10 0
0
9
3
160
20
150
30
50
130
3
-D
2
4
6
7
140
40
110
70
120
60
130
50
0
10
80
0
9
0
a, b und e
h
7
6
5
4
170
10
3
2
1
160
20
b
150
30
140
40
0
1
2
- DREIE
CK
3
4
1
3
2
0
13 0
5
g
1
GEO
2
12
60 0
a
3
11
70 0
100
80
9
0
9
0
80
100
70
110
60
120
5
10
170
c
6
7
2
16 0
0
d
Senkrechte Linien (Senkrechten) mit dem
Geodreieck zeichnen:
g
3
15 0
0
Welche Geraden sind parallel zu g?
Parallel zu g sind die Geraden:
EO
60
120
G
1
3
5 170
10
2
CK
IE
RE
1
2
1
1
0
2
Senkrecht zu h sind die Geraden:
30
150
3
h
50
130
40 0
14
a und c
3 Zeichne vier senkrechte Linien zu g
durch die Punkte P, Q, A und R.
4 Zeichne die Parallelen zu h, die durch die
Punkte Q, P, R und S verlaufen.
R
A
P
h
g
R
Q
58
S
Q
P
Längen und Abstände messen
1
Miss die Längen der Strecken mit einem Geodreieck. Gib die Längen in cm an.
C
Q
D
Beim Messen von Längen
muss das Lineal oder das Geo­
dreieck immer an der einen
Seite mit der 0 angelegt
werden.
H
L
G
K
7
6
3
2
1
0
3 cm
Länge:
___
EF
5,5 cm
__
3
50 0
QP
3
2,3 cm
110
70
100
80
9
0
9
0
80
100
70
110
60
120
Bestimme die kürzesten Abstände der Punkte A, B, C, D, und E zur Gerade g.
Abstand der
Punkte zu g
B
C
g
A
A:
2 cm
B: 3,1 cm
E
C: 1,6 cm
Um den kürzesten Abstand
zwischen einem Punkt und einer
Gerade zu messen, muss man eine
Senkrechte zu der Geraden durch
den Punkt zeichnen.
h
7
6
5
17
10 0
d
160
20
an
2
140
40
1
130
50
GE
st
1
2
3
0
O
-D
120
60
1
RE
IEC
K
2
1
110
70
3 Bestimme die kürzesten Abstände der Geraden a
und c zur Gerade g.
Abstand der
Gerade zu
c
a: 0,6 cm
g
a
0
9
3
4
2
0
10 0
8
E: 0,7 cm
Ab
150
30
D: 1,7 cm
D
4
3
0
9
3
80
10
0
70
11 0
60
120
50
130
40
140
30
150
20
160
5
10 0
17
P
6
7
Um den kürzesten Abstand zwi­
schen zwei Parallelen zu messen,
misst man die Länge der
Senkrechten.
g
nd
c: 1,6 cm
4
2
12
60 0
5 cm
3 cm
3
1
__
3
KL1
GH
10,5 cm
2
2
0
14 0
4
CD
150
30
AB
__
1
E O - DREIECK
160
20
__
__
Strecke:
2
4
Länge der roten1 SteckeG: 4 cm
B
E
5
170
10
P F
4
14 0
0
A
Absta
h
59
50 0
13
Winkel erkennen und messen
z
Winkel messen:
1. Schritt: Geodreieck mit dem Sch
eitelpunkt bei
der Null am Geodreieck anlegen.
2. Schritt: Ablesen.
Winkel bestehen aus einem Scheitelpunkt (S)
und zwei Schenkeln.
ablesen:
Sie werden mit griechischen Buchstaben bezeich­
net: a (alpha), b (beta), c (gamma)…
S
1 Miss die Größen der Winkel und trage diese in
die erste Spalte der Tabelle ein.
Winkel
Größe
Winkelart
a1
90°
Rechter Winkel
a2
95°
Stumpfer Winkel
a3
74°
Spitzer Winkel
a4
111°
Stumpfer Winkel
b1
40°
Spitzer Winkel
b2
74°
Spitzer Winkel
b3
125°
Stumpfer Winkel
b4
121°
Stumpfer Winkel
b4
b3
b2
a3
b1
a4
a1
z
a2
Winkel werden je nach ihrer Größe unterschiedlich bezeichnet.
gestreckter Winkel
2
60
überstumpfer Winkel
Schreibe die Bezeichnung der Winkel aus Aufgabe 1 in die letzte Spalte der Tabelle.
z
Winkel zeichnen
Winkel zeichnen:
1. Schritt:
Ersten Schenkel
zeichnen.
2. Schritt:
3. Schritt:
Geodreieck mit der Null am Winkel
Scheitelpunkt S anlegen. anzeichnen.
4. Schritt:
Zweiten Schenkel
zeichnen.
5. Schritt:
Winkel
benennen.
Beispiel: a = 60°
1
Zeichne die Winkel in der angegebenen Größe.
a) a = 40°
b) b = 135°
b
a
2
c
a) Miss die Winkel in der Abbildung.
a=
3
c) c = 70°
125
° b =
63
b) Zeichne die Abbildung noch einmal.
° c =
67
° d =
106
°
Zeichne die Winkel.
a) a = 45°
a
b) b = 15°
b
c) c = 210°
c
61
Rechteck und Quadrat
z
Bei einem Rechteck
– sind alle gegenüberliegenden
Seiten parallel.
– sind alle Winkel rechte Winkel.
D
Bei einem Quadrat sind
zusätzlich alle Seiten gleich
lang.
C
D
Rechtecke zeichnen:
Länge = 6 cm, Breite = 4 cm
1. Erste Seite zeichnen.
C
2. Zweite Seite senkrecht zur ersten
zeichnen.
A
1
B
A
B
Welche Figuren sind Rechtecke, welche sind Quadrate?
C
B
A
3. Dritte Seite senkrecht zur zweiten
zeichnen.
D
G
E
H
F
4. Die Enden verbinden.
Rechtecke:
A, G
Quadrate:
B, E, F
2 Ergänze die Stecken jeweils zu einem Rechteck oder
einem Quadrat.
a)
3
b)
d)
e)
Zeichne
a) ein Rechteck:
Länge: 4 cm, Breite 2 cm
62
c)
b) ein Quadrat:
Seitenlängen: 3 cm
c) ein Rechteck:
Länge 2,5 cm, Breite: 1,5 cm
Weitere Vierecke
z
Bei einer Raute sind
zusätzlich alle Seiten
gleich lang.
Bei einem
Parallelogramm
sind alle gegenüber­
liegenden Seiten
parallel.
1
Ein Drachen ist ein
Viereck, bei dem
jeweils die Nachbarsei­
ten gleich lang sind.
Ein Viereck mit nur
zwei parallelen Seiten
nennt man Trapez.
Um welche Art Viereck handelt es sich?
A: Trapez
A
B: Raute, Parallelogramm
B
C
C: Parallelogramm
D
D: Parallelogramm
E: Trapez
E
G
F
F: Parallelogramm
G: Quadrat, Rechteck
2
Verbinde die Punkte A, B, C und D zu Vierecken.
a) Markiere parallele Seiten in der gleichen Farbe
b) Kennzeichne alle rechten Winkel mit ¾.
c) Schreibe in alle Rauten ein RA, in alle Parallelo­
gramme ein P, in alle Quadrate ein Q, in die Rechtecke
ein RE und in alle Trapeze ein TR. (Tipp: in einigen
Figuren werden mehrere Abkürzungen stehen!)
D
C
A
B
A
A
B
C
C
C
D
D
B
PB
D
D
RA
P
TR
B
B
A
B
C
D
D
B
B
A
B
A
3
TR
C
Q
RE
A
B
B
C
C
C
A P
A
C
C
D
DC
D
D
D
A
Jeweils ein Eckpunkt des Parallelogramms ist
verloren gegangen. Kannst du ihn finden und das
Parallelogramm zeichnen?
A
A
C
I
63
z
Umfang und Flächeninhalt von Rechtecken
Der Umfang (u) einer Figur ist die Länge der Randlinie.
Der Umfang (u) des Rechtecks:
plus
Summe aller Seitenlängen
u=a+b+a+b
plus
Flächeninhalt (A) des Rechtecks:
Länge mal Breite
A = a ∙ b
b
b
A
u = 2 ∙ a + 2 ∙ b
plus
t
a
a
Beispiel
mal
1 Zeichne die folgenden Rechtecke und
berechne Umfang und Flächeninhalt.
3 cm
t
Start
Gegebene Werte bestimmen:
a = 2 cm, b = 3 cm
Länge
Breite
Umfang
Inhalt
a)
4 cm
3 cm
14 cm
12 ​cm​ ​
b)
2,5 cm
2 cm
9 cm
5 ​cm​ ​
c)
1,5 cm
3,5 cm
10 cm
5,25 ​cm​ ​
d)
3 cm
2,5 cm
11 cm
7,5 ​cm​ ​
2
2
cm.
b) Unterteile die Figur so in Rechtecke, dass du
den Flächeninhalt berechnen kannst.
Der Flächeninhalt beträgt 14,35
Flächeninhalt berechnen:
Formel notieren:A = a ∙ b
2
Werte einsetzen:A = 2 cm ∙ 3 cm = 6​ cm​ ​
2
2 Die Figur ist aus mehreren Rechtecken
zusammengesetzt.
a) Der Umfang beträgt 26
Umfang berechnen:
2 cm
Formel notieren: u = 2 ∙ a + 2 ∙ b
Werte einsetzen: u = 2 ∙ 2 cm + 2 ∙ 3 cm = 10 cm
2
2
3
Ein Fußballfeld ist 105 m lang und 68 m breit.
a) Wie lang ist die Seitenlinie, die um das ganze
Spielfeld herumgeht?
Rechnung:
2 ∙ 105 m + 2 ∙ 68 m = 346 m
c​ m​ ​.
Die Seitenlinie ist 346 m
2
b) Wie viel ​m​ ​Rollrasen werden für das Spielfeld
benötigt?
1,5 m
2,5 m
1,5 m
lang.
Rechnung:
1,5 m
2
105 m ∙ 68 m = 7 140 ​m​ ​
7,5 m
64
2
Man benötigt 7 140 ​m​ ​
Rasen.
z
Umfang und Flächeninhalt von Quadraten
Beim Quadrat sind alle Seitenlinien gleich lang.
u= a+a+a+a
oder
u = 4∙a
plus
Umfang
a
A
Start
a
a
mal
Beispiel
Gegebene Werte bestimmen:
a = 2 cm
1 Berechne Umfang und Flächeninhalt der
folgenden Quadrate und zeichne diese.
a
Flächeninhalt (A) des Quadrats:
Länge mal Breite
A = a∙a
oder
2
A = a (sprich: a Quadrat)
a
plus
t
plus
2 cm
Umfang (u) des Quadrats:
Summe aller Seitenlängen
Umfang berechnen:
Formel notieren: u = 4 ∙ a
Werte einsetzen: u = 4 ∙ 2 cm = 8 cm
Inhalt
Flächeninhalt berechnen:
Formel notieren: A = a ∙ a oder
2
Einsetzen: A = 2 cm ∙ 2 cm = 4 cm
2
a)
4 cm
16 cm
16 cm
b)
2,5 cm
10 cm
6,25 cm
2 cm
2
A=a
2
2
A = (2cm) = 4 cm
2
Taschenrechner
2
2 ist eine so genannte Quadratzahl
. Man kann sie einfach
mit dem Taschenrechner ausrechn
en:
2
c)
1,5 cm
6 cm
2,25 cm
d)
3 cm
12 cm
12,25 cm
Papier
Die Größen von Papier werden in
Deutschland in so genannten DINFormaten angegeben. DIN A0 ist
ein Rechteck mit einem Flächenin2
halt von ca. 1 m .
Das nächst kleinere Format DIN A1
erhält man, indem man das Blatt
in der Mitte der längeren Seite
teilt.
2
- zuerst tippt man die Zahl ein (hie
r die 2)
- dann die Taste x2 .
1 Welche Seitenlängen hat ein
Blatt des Formates DIN A2 (DIN
A3, …)?
2 Wie viele DIN-A4-Blätter sind
so groß wie ein DIN-A0-Blatt?
3 Papier wird mit verschiedenen
Gewichtsangaben gehandelt. Normales Schreibpapier wiegt 80 g
2
pro m . Wie schwer ist ein übliches
DIN-A4-Blatt?
DIN ist eine Abkürzung für
Deutsche Industrie-Norm.
65
z
Umfang und Flächeninhalt von Parallelogrammen
Umfang (u) des Parallelogramms:
Summe aller Seitenlängen
a
A = a ∙ ha oder
A = b ∙ hb
hb
ha
Die Höhe
b
b
u=a+b+a+b
u = 2∙a + 2∙b
Flächeninhalt (A) des Parallelogramms:
Grundseite mal zugehörige Höhe
a
– ist der Abstand gegenüberliegen
der
Seiten.
– ist senkrecht zur Grundseite.
1
Berechne den Umfang und den Flächeninhalt
der Parallelogramme.
ha bedeutet: Höhe auf a.
hb bedeutet: Höhe auf b.
a)
b)
2 cm
4,8 dm
3 dm
4 cm
3,6 cm
Beispiel
3,6
dm
Gegebene Werte:
a = 8 cm, b = 6 cm, ha = 5 cm
Gegebene Werte:
a = 2,0 cm b = 4,0 cm
a = 3,6 dm b = 4,8 dm
ha = 3,6 cm
hb = 3,0 dm
Umfang berechnen:
Formel:
u = 2∙a + 2∙b
Einsetzen: u = 2 ∙ 8 cm + 2 ∙ 5 cm = 26 cm
Flächeninhalt berechnen:
Formel: A = a ∙ ha
2
Einsetzen: A = 8 cm ∙ 5 cm = 40 m
Umfang berechnen:
u = 2 ∙ 2 cm + 2 ∙ 4 cm
= 12 cm
u = 2 ∙ 3,6 dm + 2 ∙ 4,8 dm
= 16,8 dm
Jedes Parallelogramm lässt sich
leicht in ein Rechteck mit dem glei
chen Flächeninhalt verwandeln.
Flächeninhalt berechnen:
A = 2 cm ∙ 3,6 cm
2
2
= 14,4 dm
ha
a
a
Berechne Umfang und Flächeninhalt der Parallelogramme.
a)
b)
c)
d)
Werte:
a = 12 cm
b = 4 cm
h = 7 cm
a = 15 cm
b = 13 cm
h = 20 cm
a = 2,5 m
b = 3,4 m
h = 3,2 m
a = 12,5 dm
b = 8,4 dm
h = 20,2 dm
Umfang:
2 ∙ 12 + 2 ∙ 4
= 32 cm
2 ∙ 15 + 2 ∙ 13
= 56 cm
2 ∙ 2,5 + 2 ∙ 3,4
= 11,8 m
2 ∙ 12,5 + 2 ∙ 8,4
= 41,8 dm
12 cm ∙ 7 cm
2
= 84 cm
15 cm ∙ 20 cm
2
= 300 cm
2,5 m ∙ 3,2 m
2
= 8m
12,5 dm ∙ 20,2 dm
2
= 25,25 dm
Flächeninhalt:
66
ha
2
= 7,2 cm
t
A = 3,6 dm ∙ 4 dm
Umfang und Flächeninhalt von Dreiecken
Umfang des Dreiecks:
Summe aller Seitenlängen
z
Flächeninhalt des Dreiecks:
Grundseite mal zugehörige Höhe
geteilt durch 2
C
c ∙ hc
A = ____
2
a
b
U=a+b+c
hc
A
A = c ∙ hc : 2
oder
B
c
SE84103800_G_094_01.eps
1 Berechne den Umfang und den
Flächeninhalt der Dreiecke.
b)
27
6,2 cm
mm
34 mm
Beispiel
hc = 3,9 cm
ha = 27 mm
a = 4,3 cm
b = 31 mm
b = 5,9 cm
c = 34 mm
c
7,0
6,0 m
Gegebene Werte:
c = 6 cm, a = 3,6 cm, b = 7 cm, hb= 3,1 cm
Umfang berechnen:
u = 36 mm + 31 mm + 34 mm
= 101 mm
Umfang berechnen:
Formel: u = a + b + c
Einsetzen: u = 7 cm + 6 cm + 3,6 cm
= 16,6 cm
Flächeninhalt berechnen:
Formel:
2
= 12,09 cm
t
b ∙ hb
A = ____
2
7 cm ∙ 3,1 cm
Flächeninhalt berechnen:
A = 6,2 cm ∙ 3,9 cm : 2
m
m
a = 36 mm
3,1
c = 6,2 cm
= 16,4 cm
c
Beispiel:
Gegebene Werte:
u = 6,2 cm + 4,3 cm + 5,9 cm
hc
mm
3,9 cm
36
m
cm
4,3 cm
5,9
Setzt man zwei
Dreiecke zusammen,
erhält man ein
Parallelogramm:
3,6 m
a)
c
31 m
t
Der Bruchstrich steht für „geteilt durch“.
Einsetzen: A = _______
2
= 10,85 cm
A = 36 mm ∙ 27 mm : 2
2
2
= 486 mm
2 Berechne die Flächeninhalte der Dreiecke. Miss die fehlenden Längen mit dem Lineal und
beschrifte sie.
a) A = 4 cm ∙ 2,5 cm : 2
a)
b)
c)
2
= 5 cm
b) A = 3,5 cm ∙ 2 cm : 2
2
= 3,5 cm
67
Flächeninhalt von Vielecken
z
Den Flächeninhalt von Vielecken A1: Dreieck
kann man berechnen, indem man
sie in geeignete Teilflächen (Drei- A2: Rechteck
ecke, Rechtecke, Trapeze) zerlegt.
A3: Parallelogramm
Die Inhalte der Teilflächen werden dann zusammengezählt.
t
Vieleck
aufteilen in Teilflächen
1
Berechne den Flächeninhalt der Vielecke.
Teile das Vieleck in Teilflächen auf und miss die Längen
der benötigten Strecken.
a)
b)
A1
A2
Teilfläche 1:
Teilfläche 1:
Vieleck aufteilen in Teilflächen:
A1: Dreieck
A2: Parallelogramm
Art: Rechteck
Art: Dreieck
Flächeninhalt des Dreiecks A :
1
Gegebene Werte:
Gegebene Werte:
a = 1,5 cm
a = 1,5 cm
ha = 1,5 cm
Formel:
Formel:
A = a∙b
A = ___
2
2. Formel:
A = ___a
a∙h
2
Einsetzen:
Einsetzen:
A = 1,5 cm ∙ 1 cm
1,5 cm ∙ 1,5 cm
A = ________
2
A=
6___
cm ∙___
3 cm
=
2
Flächeninhalt des Parallelogramms
a ∙ ha
2
a = 6 cm, h = 3 cm
a
3. Einsetzen:
b = 1 cm
= 1,5 cm
1. Gegebene Werte:
9 cm2
A2:
1. Gegebene Werte:
a = 6 cm, h = 3 cm
a
2. Formel:
A = a∙h
a
2
= 1,125 cm
3. Einsetzen:
A = 6 cm ∙ 3 cm = 18 cm2
Flächeninhalte der Teilfiguren add
ieren:
A = A1 + A
Teilfläche 2:
Teilfläche 2:
Art: Dreieck
Art: Trapez
Gegebene Werte:
Gegebene Werte:
a = 2 cm
a = 4,5 cm, c = 1,5 cm
Summe der Teilflächen bei Figur a):
ha= 1 cm
h = 1,5 cm
1,5 cm + 1 cm = 2,5 cm
Formel:
Formel:
Summe der Teilflächen bei Figur b):
A=
a ∙ ha
___
2
A=
(a + c)
____
2 ∙h
Einsetzen:
2 cm ∙ 1 cm
A = ______
2
A = __________
∙ 1,5 cm
2
2
68
A = 9 cm + 18 cm2 = 27 cm2
2
Einsetzen:
= 1 cm
2
2
(4,5 cm + 1,5 cm)
2
= 4,5 cm
2
2
2
2
2
1,125 cm + 4,5 cm = 5,625 cm
Hinweis:
Es gibt jeweils mehrere
Lösungsmöglichkeiten.
Kreisumfang
z
M Mittelpunkt
d Durchmesser
r Radius
Der Kreisumfang lässt sich mit Hilfe der Kreiszahl π (Pi) berechnen.
d
u = π∙d
r
d
d
d
M
d
u
π hat den Wert 3,14159265…
Es reicht aber aus, mit dem gekürzten Wert 3,14 zu rechnen.
t
t
1
Beispiel
Berechne den Umfang der Kreise mit dem angegebenen
Durchmesser.
d = 1,5 cm
a)
b)
c)
d)
Durchmesser
8,0 cm
4,5 cm
14,5 cm
0,75 cm
Umfang
25,12 cm
14,13 cm
45,53 cm
2,355 cm
d
Formel: u = π ∙ d
Einsetzen: u = 3,14 ∙ 1,5 cm
= 4,71 cm
2
Bei einem Hochrad hat das Vorderrad einen Durchmesser von
1,40 m und das Hinterrad einen Durchmesser von 43 cm.
a) Bestimme die Umfänge in m.
Vorderrad: 4,396 m
Hinterrad: 1,35 m
b) Wie oft drehen sich die Räder auf einer Strecke von 1 Kilometer?
Runde auf ganze Umdrehungen.
Vorderrad: 227 mal
t
Hinterrad: 741 mal
3
Berechne zu den abgebildeten Kreisen zunächst den Umfang. Runde auf ganze Millimeter.
Zeichne dann eine Strecke, die so lang ist wie der berechnete Umfang des Kreises.
a)
b)
d = 20 mm
u ≈ _____
63 mm
c)
d = 30 mm
94 mm
u ≈ ______
d)
d = 40 mm
126 mm
u ≈ ______
d = 50 mm
157 mm
u ≈ ______
a)
b)
c)
d)
69
z
Kreisinhalt
Beispiel
d = 3 cm
Flächeninhalt des Kreises:
A = π ∙ r ∙ r oder
2
A = π∙r
Radius ausrechnen:
d
r = _2 = _32 cm = 1,5 cm
Der Durchmesser d ist doppelt
so groß wie der Radius.
r
d = 2∙r
d
r = __
2
t
t
t
1
d
d
r
2
Formel: A = π ∙ r ∙ r
A = π∙r
Einsetzen:
A = π ∙ 1,5 cm ∙ 1,5 cm
A = 3,14 ∙ 1,5 cm ∙ 1,5 cm
2
= 7,065 cm
A = π ∙ (1,5 cm)
2
A = 3,14 ∙ 2,25 cm
2
= 7,065 cm
2
Berechne den Flächeninhalt der Kreise mit dem angegebenen Radius.
a)
b)
c)
d)
e)
Radius
5,0 cm
3,4 cm
6,0 cm
3,2 cm
3,25 cm
Umfang
75,5 cm
2
36,3 cm
2
2
113,04 cm
2 Berechne den Flächeninhalt der Kreise mit
dem angegebenen Durchmesser.
a)
b)
Durchmesser
8,0 cm
9,8 cm
Radius
4 cm
4,9 cm
Umfang
50,24 cm
2
32,15 cm
2
2
33,17 cm
3 Wie groß ist die Fläche eines 10-ct-Stücks?
Schätze zunächst.
cm2
2
Miss den Durchmesser: ca. 19 mm
2
Berechne den Flächeninhalt. ca. 2,3 cm
2
75,39 cm
4 Wie groß ist die dunkelorange Fläche? Berechne zunächst den Flächeninhalt des großen Kreises und
dann den der kleinen Kreise.
Flächeninhalt des großen Kreises:
2
2
2
A = π ∙ (4 cm) = π ∙ 16 cm = 50,24 cm
2 cm
Flächeninhalt eines kleinen Kreises:
2
2
2
A = π ∙ (2 cm) = π ∙ 4 cm = 12,56 cm
Größe der dunkelorange Fläche:
2
2
2
2
50,24 cm – 12,56 cm – 12,56 cm = 25,12 cm
70
Test: Flächenberechnung
1
Berechne den Umfang und den Flächeninhalt der Rechtecke.
2 cm
u = 12 cm
2
A = 8 ​cm​​ ​
a = 4 dm b = 23 cm
u = 14,6 cm
u = 126 cm
2
2
A = 12 ​cm​​ ​
4 cm
2
a = 2,5 cm b = 4,8 cm

A = 920 c​m​​ ​


u = 12 cm A = 7,77 cm​ ​


A = 5 ​cm​​ ​
7 cm
32 c
4 cm
m
30 cm
m
Berechne den Umfang und den Flächeninhalt der Figuren.
40 cm
32 c

6c
m
40 cm
2
u = 144 cm A = 1 200 ​cm​ ​

m
5,2 cm
m
6c
6c
60 mm
6 cm
2
2
A = 900 ​mm​​ ​
4
2
Berechne den Flächeninhalt der Dreiecke.
30 mm
3
2
u = 26 cm A = 28 ​cm​ ​

A = 15,6 ​cm​​ ​
2

Berechne den Umfang und den Flächeninhalt der Kreise mit den angegebenen Maßen.
d = 5 cm
d = 6,8 cm
u = 15,7 cm
u = 21,35 cm
2
u = 52,75 cm
2
A = 19,625 ​cm​ ​
2
A = 36,3 ​cm​ ​
Bronze:
r = 8,4 cm

Silber:
Gold:
A = 221,56 ​cm​ ​


(Richtig gelöste Aufgaben ankreuzen. Die Lösungen
findest du auf Seite 78.)
71
Geometrische Körper
Fläche
Würfel
Quader
Pyramide
Ecke
Prisma
Kante
Zylinder
Kegel
Über eine Fläche streicht man
mit der Handfläche.
Kugel
SE84746491_G_K06_114_02.eps
An einer Kante fährt man mit
dem Finger entlang.
Eine Ecke berührt man nur mit
der Fingerspitze.
1
Welche Körper erkennst du in den Abbildungen?
2
1
3
Bild 1: Pyramide
Bild 2: Zylinder
Bild 3: Quader
Bild 4: Würfel
4
2
Fülle die Tabelle aus.
Anzahl der
Flächen
Anzahl der
Kanten
Anzahl der
Ecken
72
Bild 5: Kugel und Kegel
5
Pyramide
Quader
Kugel
Zylinder
Würfel
Kegel
5
6
1
3
6
2
8
12
0
2
12
1
5
8
0
0
8
0
Schrägbilder zeichnen
1
Ein Würfel ist ein Quader, bei dem alle Seiten
gleich lang sind. Vervollständige zu einem Schrägbild.
Schrägbild eines Quaders zeichnen:
Länge 4 cm, Breite 2 cm, Höhe 1,5 cm
1,5 cm
1. Vorderfläche zeichnen.
4 cm
2. Nach hinten laufende
Kanten schräg und verkürzt zeichnen. Für 1 cm
Seitenlänge zeichnet man
eine Kästchendiagonale.
2
Vervollständige die Schrägbilder.
3. Die Endpunkte verbinden. Die nicht sichtbaren
Kanten werden gestrichelt.
3 Zeichne das Schrägbild nach und trage alle
verdeckten Kanten ein.
4
Zeichne eine Pyramide mit der Höhe h = 2 cm.
Schrägbild einer Pyramide zeichne
n:
1. Grundfläche zeichnen.
2. Höhe auf die Mitte der
Grundfläche zeichnen.
3. Höchsten Punkt mit der
Grundfläche verbinden.
73
z
Rauminhalt (Volumen) von Quadern berechnen
Beispiel
1 cm
Gegebene Werte:
Formel: Einsetzen: a
a = 4 cm b = 2 cm,
c = 1 cm
V = a ∙ b ∙ c
3
V = 4 cm ∙ 2 cm ∙ 1 cm = 8 ​cm​ ​
4 cm
1
12,1 cm
9,5 dm
d)
m
5d
m
6,
6,
5,5 cmzusammengesetzten
5,5 cm
Berechne das Volumen der
Quader.
4 dm
dm
80
0,
20 dm
5 cm
m
2c
3,
3 cm11 cm
2,5 cm
5 cm
4,4 cm
5 cm
6
20 dm
80
m
11 cm
m
4,5 dm
dm
e)
3,
f)b)
f)
0,
8 dm
0,5 m
2c
m
5 cm
2,5 cm
3,4 dm
10
a)
e)
15 cm
2 dm
3
Quader 1: 75 ​cm​ ​
Quader 2: 108 ​dm​ ​
3
Quader 2: 330​ cm​ ​
3
Gesamt:
Quader 1: 160 ​dm​ ​
Gesamt:
74
268 ​dm​ ​
3
3
3
405 ​cm​ ​
80
0,
20 dm
5d
5d
2
3,4 dm
0,5 m
t
m
m
2,5 cm
= 209,95 d​m​ ​
m
3
= 326,7 c​m​ ​
11 cm
2c
3
f)
Ve)= 3,4 dm ∙ 6,5 dm ∙ 9,5 dm
3,
3
= 36 c​m​ ​
5 cm
6c
d)
V = 4,5 cm ∙ 6 cm ∙ 12,1 cm
0,5 m
d)
5,5 cm
3,4 dm
2,7 m
V = 4 cm ∙ 3 cm ∙ 3 cm
4,5 cm
9,5 dm
9,5 dm
4,5 cm
6c
c)
m
m
4 cm
c)
4,5 cm
6,
4 cm
c)
3c
3c
m
m
3 cm
3 cm
b)
2,7 m
b)
a)
2,7 m
a)
6c
m
Berechne das Volumen der Quader.
12,1 cm
t
b)
3 cm
Höhe
b
Breite
a)
c
67777899990 67777899990 67777899990
Länge
2 cm
4 cm
3c
m
V = a ∙ b ∙ c
12,1 cm
Der Rauminhalt (das Volumen) des Quaders:
Länge mal Breite mal Höhe
z
z
Rauminhalt (Volumen) von Würfeln berechnen
Der Rauminhalt (das Volumen) des Würfels:
Länge mal Breite mal Höhe
Da beim Würfel alle Seiten gleich lang sind, gilt:
V=a
67777899990
Länge
∙
a
677789990
∙
Breite
a
3
a = a
a
677789990
a
Höhe
Beispiel
14 dm
Taschenrechner
143 mit dem Taschenrechner berechne
n:
– 14 eintippen
– Taste x oder ^
– 3 eintippen
dm
y
14
14 dm
Gegebene Werte: a = 14 dm
3
Formel:
V = a∙a∙a
oder
V=a
3
Einsetzen: V = 14 dm ∙ 14 dm ∙ 14 dm
V = (14 dm)
3
3
= 2 744 dm
= 2 744 dm
t
1
Berechne das Volumen der Würfel.
a)
b)
c)
d)
e)
Kantenlänge
2,5 cm
1,4 dm
8,7 mm
24 cm
0,4 m
Volumen
15,625 cm3
2,744 dm3
658,503 mm3
13 824 cm3
0,064 m3
Schachteln falten
Nimm ein DIN A4-Blatt und falte es nach den Anweisungen. Du erhältst eine Schachtel, wie sie das
Foto zeigt. Miss die Kantenlängen und berechne die Rauminhalte.
Offener Quader
Offener Würfel
SE74746371_G_K06_122_schachtel_02.eps
Den oberen und unteren
SE74746371_G_K06_122_schachtel_07.eps
SE74746371_G_K06_122_schachtel_06.eps
Ein Papierquadrat mehrEinen Streifen abschneiden,
Die obere Hälfte auf die untere
SE74746371_G_K06_122_schachtel_10.eps
Rand zur Mitte falten.
fach falten.
die schrägen Linien falten
falten.
SE74746371_G_K06_122_schachtel_03.eps
Die vier Ecken nach
innen falten.
SE74746371_G_K06_122_schachtel_08.eps
SE74746371_G_K06_122_schachtel_11.eps
Die vier Ecken nach innen falten.
Den unteren Teil auf den SE74746371_G_K06_122_schachtel_12.eps
An der Markierung nach oben
oberen falten.
ziehen.
Ein DIN-A4-Blatt mehrSE74746371_G_K06_122_schachtel_01.eps
mals falten und wieder
öffnen.
SE74746371_G_K06_122_schachtel_04.eps
Die inneren Ränder nach außen
falten; anschließend nach oben
ziehen.
Wenn die dreieckigen Spitzen in den
„Taschen“ außen am Würfel stecken, ist
der Würfel fertig.
75
Netze zeichnen
Faltet man einen Quader auseinander, so erhält man
das Netz eines Quaders.
Br
ei
te
Höhe
Breite
Höhe
Länge
Länge
1
Die Abbildung rechts zeigt ein unvollständiges Quadernetz.
a) Welche Längen haben die Kanten?
Länge
Breite
Höhe
2 cm
1,5 cm
1 cm
b) Zeichne das vollständige Quadernetz.
c) Färbe gegenüber liegende Flächen
in der gleichen Farbe.
Zeichne die Netze des Quaders und des Würfels.
cm
2 cm
2
1 cm
0,5
3 cm
Tipp:
1 cm
3
Welche der folgenden Figuren stellt ein Quadernetz dar? Kreuze die richtige Figur an.

76
1c
m
Ein Würfel ist ein Quader, bei
dem alle Seiten gleich lang
sind.


