dspace cover page - ETH E

Research Collection
Doctoral Thesis
Über Kegelschnitte in der hyperbolischen Geometrie
Author(s):
Leutenegger, Emil
Publication Date:
1923
Permanent Link:
https://doi.org/10.3929/ethz-a-000103747
Rights / License:
In Copyright - Non-Commercial Use Permitted
This page was generated automatically upon download from the ETH Zurich Research Collection. For more
information please consult the Terms of use.
ETH Library
Über
Kegelschnitte
in der
hyperbolischen Geometrie
Von der
Technischen Hochschule in Zürich
Eidgenössischen
zur
Erlangung
der
Würde eines Doktors der Mathematik
genehmigte
Promotionsarbeit
vorgelegt
von
Emil Leutenegger
aus
Eschlikon und Braunau
Referent:
Herr Prof. Dr.
M. Großmann
Korreferent: Herr Prof. Dr. L. Kollros
336
»muH*-
Druck
von
Huber & Co. in Frauenfeld 1923
Meinen lieben Eltern
Einleitung.
In der
in
Arbeit sollen
vorliegenden
hyperbolischen Geometrie
der
fassung
der
Dadurch,
gebracht.
Allgemeinheit
ohne
sind
so
Kegelschnitt
ausgeführt,
durch ausschließliche
einem
zu
Zeichnen
von
einem Punkt
1
1
N. I.
D.
einen Kreis als
Lobatschefskij
H. Liebmann
deutschen
8
an
Schnittpunkte
:
:
Zwei
im
der Konstruktion des
zu
Wir nehmen auch an, daß die Instrumente
seien, womit auch die Möglichkeit
Tangenten
von
betrachten ist.*
geometrische Abhandlungen, deutsch
von
F.
Engel.
Die elementaren Konstruktionen der nichteuklidischen Geometrie.
Mathematikervereinigung. Bd. 20, S. 56—69.
Hubert: Neue Begründung der Bolyai-Lobatschefskij'schen
K. Dändliker : Darstellende
Ebene
Gebiet durch¬
gemeinschaftlichen
einer Geraden mit einem Kreis und der
gegeben
Abbildung
hyperbolischen
eigentlichen
Geometrie.
S. 137-150.
4
zur
Auf¬
Parallelenkonstruktionen,1 der Konstruk¬
Kreisen und Abstandslinien vorhanden
der Konstruktion der
projektive
beeinträchtigt.
sie auch in der
Operationen
gegebenen Parallelwinkel,2
Lotes zweier sich nicht schneidender Geraden.3
zum
daß
werden können auf Grund der bekannten
tion des Lotes
auf eine
Kegelschnitte
als Kreis angenommen wurde, wird die
der Sätze und Konstruktionen in keiner Weise
projektive Grundlage,
geführt
Gestützt
auf die Euklidische Ebene
ist dieselbe
daß der absolute
Alle Konstruktionen
'
und Konstruktionen der
untersucht werden.
Ebene
hyperbolischen
Eigenschaften
hyperbolische Geometrie.
Diss. Zürich 1919.
S. 256.
Jahresberichte der
Math. Annalen Bd. 57.
Leer
-
Vide
-
Empty
I.TEIL
Allgemeines
§
eigentliche
hyperbolischen Geometrie.
der
Hauptsätze
Definitionen und
1.
1. Jede.
Kegelschnitte
über
hyperbolischen
Gerade der
hyperbolischen Geometrie.
der
Ebene besitzt 2 unendlich ferne Punkte
„Enden."1
oder
2. Die Gesamtheit aller unendlich fernen Punkte der Ebene ist ein
Kegelschnitt,
fallender
reeller, nicht
zer¬
»Absolute Kegelschnitt" (A. K.).
der sog.
3. Die Punkte der Ebene, die im Innern des A. K. liegen, mögen als »eigentliche",
diejenigen außerhalb des A. K. dagegen als „uneigentliche* Punkte bezeichnet werden. Die
uneigentlichen Punkte sei das eigentliche, bezw. un¬
eigentliche „Gebiet" genannt. Die Grenze wird gebildet durch die Punkte des A. K., die
„absoluten" Punkte. Für ein Wesen des eigentlichen Gebietes der hyperbolischen Ebene
sind sowohl die absoluten, als auch die uneigentlichen Punkte unzugänglich.
Ebenso unterscheiden wir zwischen eigentlichen, uneigentlichen und „isotropen" Ge¬
raden, je nachdem dieselben den absoluten Kegelschnitt schneiden, nicht schneiden oder
Gesamtheit aller
bezw.
eigentlichen,
berühren.
in einem eigentlichen, einem un¬
Wesen ergeben sich
hyperbolisches
eigentlichen
in Bezug auf die gegenseitige Lage zweier Geraden die drei Möglichkeiten: zwei Gerade
schneiden sich, schneiden sich nicht oder sie sind parallel.
5. Jeder Geraden ist ein sog. „absoluter Pol" zugeordnet, der Schnittpunkt aller Lote
Ist die Geradev eigentlich, so ist ihr absoluter Pol un eigentlich und um¬
zur Geraden.
gekehrt. Ebenso besitzt jeder Punkt eine sog. „absolute Polare"; es ist diejenige Gerade,
welche alle Strahlen durch den Punkt rechtwinklig schneidet. Zwei sich nicht schneidende
Gerade besitzen infolgedessen ein „gemeinschaftliches Lot", das eine eigentliche Gerade
Zwei
4.
eigentliche
Gerade treffen sich
oder in einem absoluten Punkt.
entweder
Für ein
darstellt.
6. Der Abstand zweier Punkte
ä
wo
U, V die Enden
A,
=
B ist definiert durch die Formel
clg (ABUV),
der Geraden AB bedeuten und
Der Winkel zweier Geraden a, b ist
ep
wo
u,
reelle,
1
v
die
=
*
-
c' -lg
gegeben
(abiiv),
Tangenten vom Schnittpunkt
beliebige Konstante ist.
sonst aber
D. Hubert: siehe S. 1.
c
eine
beliebige,
reelle Konstante ist.
durch:
(i
=
V— 1)
der Geraden
an
den A. K. und c' eine
zweite
4
imaginär, je nachdem entweder beide
verschiedenartig sind.
Der Winkel zweier Geraden ist reell, wenn dieselben sich im Eigentlichen schneiden.
Er wird gleich 0, wenn die Geraden parallel sind.
Der Winkel zweier Geraden, die sich
reell
ist
oder
im Uneigentlichen schneiden,
imaginär, je nachdem die beiden Geraden ver¬
schiedenartig oder aber beide eigentlich oder beide uneigentlich sind.
Die Winkelfunktion ist im übrigen unendlich vieldeutig mit einer Periode gleich 2 7t.
Zwei nichtschneidende Gerade haben, wie schon erwähnt, einen gemeinschaftlichen
7. Der
Punkte
zweier Punkte
Abstand
oder
eigentlich
uneigentlich
reell oder
ist
oder aber
•
senkrechten Abstand.
Derselbe ist
ß
dem mit
gleich
Winkel der Geraden.
multiplizierten
-t—,
1G
8. Ist
Gleichung
die
des A. K. in
+ k2 x*
¥ x*
=
(äxx
—
xs*
=
0
Punktkoordinaten,
Qg^^ + y-^y^O
dieselbe in Linienkoordinaten, und setzen wir
,>
so
_
8">Xx
v
,
xy=^
0
.,
~dxTyi'
,
_
v
&=^
d%
"sir
^''
lassen sich die Formeln für den Abstand und den Winkel in die Form
(Jcä)
ch
*"
=
V U>XX
(jc^^l-^-^y + ^y^
sh
=,
V
tövy\yy
•
bringen:
y
(Ûxx
•
iäyy
V-"«-co)y + ^-
2
th
cos
<p
(ft.d)=
=
iÙXy
sin
=,
cp
—
'11
Hiezu tritt noch eine Formel für den senkrechten Abstand eines Punktes A
einer Geraden
von
a
sh
wo
Çx
=
5i
*i
-{- 5a
*2
H~ ?3 ^3
(*
und
d)
•
Çx
=
Gerade darstellt.
9. Ist
Qg,j
jeder
xs)
0
,
die
Bedingung
der
Inzidenz
von
Punkt und
i
=
Ist (axy
xv
i-Jc'^
=
0,
so
wird tp
7t
=
d. h. 2 Gerade stehen zueinander
-^-,
durch den absoluten Pol der andern hindurch
10.
(xv
(Ç1} £2, £.,):
=
0,
so
wird d
t
=
•
TC
—„—.
auf der absoluten Polaren des andern
normal,
wenn
Punkte,
von
jede
geht.
Wir bezeichnen zwei solche
liegt,
als
,orthogonale"
Punkte.
denen
5
§
Zusammenhang mit der Theorie der Polarsysteme.
2.
Irgend ein Kegelschnitt ist bestimmt als Pol- (und zugleich Polar-) -kegelschnitt eines
Polarsystems, d. h. einer involutorischen Reziprozität, einer linearen Zuordnung .von Punkten
und Geraden, die sich analytisch in die Form bringen läßt:
p
•
£/
h
p
wo
i
=
\, 2, 3 und
koordinaten
Die
««=«*/.
li
•
ZaiiXk,
=
=
=
k
1,2,
S am
=
x'k,
l,2,3
Gleichung
Kegelschnitts
des
lautet dann in Punkt¬
:
i, k
in Linienkoordinaten:
ts
wo
die Aik
selben
2.
sind.
Ordnung
gleich
;, k
adjungierten Unterdeterminanten der a«
folgt, daß jeder Kegelschnitt aufgefaßt
den
Daraus
in der Determinante der¬
werden
kann
als
Kurve
oder als Kurve 2. Klasse.
Der Polkegelschnitt ist
Reziprozität entsprechenden
geometrische Ort
der
der
Punkte, die mit den
ihnen in der
Geraden inzident sind.
Anderseits' ist durch die °o2 Geraden und ihre absoluten
zweites
Pole, bezw. durch die Postulate
Polarsystem bestimmt,
Bewegung
sog. absolute Polarsystem, dessen
im
der
Falle
absolute
Polkegelschnitt,
hyperbolischer Maßbestimmung reell ist
Kegelschnitt,"
und, bezogen auf eines seiner Polardreiecke, durch die Gleichung dargestellt werden kann :
ein
der
das
Wxx
=
Je2 '£\
+
&2
#22
—
#32
=
0
resp.
%
Die metrischen
infolgedessen
sich
Eigenschaften
ableiten
projektiven Eigenschaften
§
3.
=
aus
^ + ^_FC32=0.
Kegelschnitte in der hyperbolischen Geometrie lassen
Beziehungen der beiden Polarsysteme, d. h. aus den
Kegelschnitte w und ft.
der
den
der beiden
Mittelpunkte, Achsen, Asymptoten
Zwei
Kegelschnitte
gegebenen Kegelschnitt
besitzen stets ein
und
Brennpunkte
der
Kegelschnitte.
Für einen beliebig
Polardreieck.
Tripel orthogonaler Punkte, bezw.
ein solches normaler Geraden dar und der gegebene Kegelschnitt besitzt Symmetrieeigen¬
schaft in Bezug auf jeden dieser 3 Punkte, resp. auf jede der 3 Geraden.
Mit anderen
Worten: die Ecken des gemeinsamen Polardreiecks sind die 3 Mittelpunkte, die Seiten
dagegen die 3 Achsen des gegebenen Kegelschnittes. Von diesen 3 Mittelpunkten ist sicher
einer reell, während die beiden andern reell oder imaginär werden können, Dasselbe gilt
gemeinsames
und den A. K. stellt dasselbe ein
•
auch
von
den Achsen.
Von
des A. K. zusammenfallen.
den 3
Mittelpunkten
können 2 oder alle 3 in einem Punkt
6
Zwei
Kegelschnitte
haben
schnitt besitzt. 4 reelle oder
im
allgemeinen
4
paarweise imaginäre
gemeinsame Punkte,
absolute Punkte,
von
d. h.
jeder Kegel¬
denen aber auch 2
oder mehr zusammenfallen können.
Jede Verbindungsgerade zweier getrennter oder kon¬
Kegelschnittes bezeichnen wir als Asymptote desselben.
Der allgemeine Kegelschnitt besitzt somit in der hyperbolischen Geometrie 6 reelle oder
paarweise imaginäre Asymptoten. Den Pol einer Asymptote in Bezug auf den A. K. nennen
wir Asymptotenpunkt, denjenigen in Bezug auf den gegebenen Kegelschnitt Leit¬
punkt. Die Asymptotenpunkte vertreten die Asymptoten bei den Konstruktionen, sobald
die Asymptoten uneigentlich werden.
Ebenso besitzen ein gegebener Kegelschnitt und der A. K. im allgemeinen 4 gemein¬
Da in besondern
same Tangenten, die sich paarweise in je einem Brennpunkte schneiden.
Fällen auch 2 oder mehrere der isotropen Tangenten eines Kegelschnittes zusammenfallen
können, so reduziert sich dann die Zahl der Brennpunkte, die im allgemeinen 6 ist. Die
absolute Polare eines Brennpunktes nennen wir Brenngerade, die Polare eines solchen
in Bezug auf den Kegelschnitt dagegen Leitgerade.
Diese Definitionen der Mittelpunkte, Achsen, Asymptoten und Brennpunkte stimmen
mit den Euklidischen Definitionen überein, resp. gehen in diese über durch geeigneten
Grenzübergang. Dagegen werden die Asymptotenpunkte in der Euklidischen Geometrie
sekutiver absoluter Punkte eines
zum
Teil
zu
Punkten
der unendlich
eigentlichen Mittelpunkt
zusammen,
fernen Geraden,
desgleichen
die
zum
Teil fallen sie mit dem einen
Leitpunkte.
Die reellen
werden in der Euklidischen Geometrie identisch mit der unendlich fernen
zwei reelle
eigentliche Leitgerade übrig
§
4.
Brenngeraden
Geraden, während
bleiben.
Einteilung der Kegelschnitte.
Kegelschnitte der hyperbolischen Geometrie lassen sich nach ihrer Lage zum A. K.
in 5 Hauptgruppen einteilen:1
I. Allgemeine Kegelschnitte, d. h. solche, die den A. K. in 4 getrennten, paarweise
Wir unterscheiden: Ellipsen (4 imaginäre
reellen oder imaginären Punkten schneiden.
absolute Punkte), Hyperbeln (4 reelle absolute Punkte) und Semihyperbeln (2 reelle,
2 imaginäre absolute Punkte). Ellipsen und Hyperbeln sind sog. Mittelpunktskegelschnitte,
d. h. solche mit einem eigentlichen Mittelpunkt und zwei eigentlichen Achsen. Die Semi¬
hyperbeln besitzen nur einen uneigentlichen Mittelpunkt und eine eigentliche Achse.
II. Parabeln. Dies sind Kegelschnitte, die den A. K. in einem Punkt berühren und in
zwei getrennten Punkten schneiden.
Sie besitzen eine eigentliche Achse.
Sie stehen mit dem A. K. in doppelter Berührung.
III. Kreise und Abstandslinien.
Ein eigentlicher oder uneigentlicher Mittelpunkt, dazu eine uneigentliche oder eigentliche
Die
Achse.
IV. Oshulierende Parabeln.
noch in einem vierten Punkt.
punkt, seine Tangente
1
die
Sie berühren
Der
Oskulationspunkt
einzige, isotrope Achse.
Vgl. Gertr. Scheben : Brennpunkte
Diss.
Bonn, 1921.
Geometrie.
den A. K.
und
dreipunktig und schneiden ihn
einzige, aber absolute Mittel¬
ist der
Asymptoten der Kegelschnitte
in
der Nicht-Euklidischen
7
V. Grenzkreise.
Dies sind
Kegelschnitte, die den A. K. vierpunktig berühren. Der
einzige, aber absolute Mittelpunkt, seine Tangente die einzige,
Berührungspunkt
isotrope Achse.
Diese Einteilung und die Kriterien für die verschiedenen Haupttypen von Kegelschnitten
ergeben sich auf einfache Weise mit den Mitteln der Invariantentheorie. Wenn wir aber,
wie es hier geschehen soll, auf die Realitätsverhältnisse der Asymptoten und Brennpunkte
eingehen wollen, so erhalten wir eine größere Anzahl von verschiedenen Kurventypen.1
ist
I. Die
Gleichung
der
„Mittelpunktskegelschnitte"
aller
Kxx
ön Xx -f- ß22 3/2
=
~\- °3S #8
==
kann auf die Form
"•
gebracht
werden:
(flll -5* a2v)
Wir unterscheiden:
1. Die
imaginäre Ellipse.
an > a22 > 0 >
Die
Kurve
hat
keine
2 nicht dazu
Asymptoten,
2. Die
—
k2 ass oder
—
¥ ass > 0 > an > a22.
Sie besitzt 2 uneigentliche
reellen Punkte und Tangenten.
homologe Brennpunkte, die aber eigentlich sind.
eigentliche Ellipse.
^2 «33 >" ^ °^er 0 ^*
ail > «22 >
&2 «33 > «11 > «221
Die Kurve
liegt ganz im eigentlichen Gebiet, hat weder absolute Punkte noch isotrope
Sie besitzt 2 uneigentliche Asymptoten und 2 zu diesen homologe eigentliche
Tangenten.
Brennpunkte.
3. Die
Auf der Kurve
iineigentliche
liegen
konkave
0 > «ii > «22 >
Die Kurve
liegt
ganz
im
—
4
zugängliche Scheitelpunkte.
Ellipse.
&2 ß83 oder
uneigentlichen
—
k2 aS3 > alt > a22 > 0.
Gebiet.
Im
übrigen
ist alles genau
gleich
wie im Fall 2.
4. Die konkave
au >
Hyperbel.
—
(Hyperbel
Mittelpunkt
mit innerem
k2 aS3 > a22 > 0 oder 0 > an >
Es existieren 4 absolute Punkte und 4
—
bei
Liebmann)
7c2 a3S > a22.
eigentliche Asym¬
völlig getrennte Aste, die
uneigentliche Brennpunkte.
in Bezug auf den eigentlichen Mittelpunkt konkav gekrümmt sind.
Auf jedem derselben
liegt ein zugänglicher Scheitelpunkt. Die uneigentliche Achse wird nicht geschnitten.
ptoten
isotrope Tangenten,
also 6
Die Kurve besitzt zwei
und 6
5. Die konvexe
au >
Hyperbel.
—
(Hyperbel
mit äußerem
Mittelpunkt
bei
Liebmann)
7c2 aS3 > 0 > a22 °^er «u ~> 0 > ^2 «33 > «22-
Punkte, keine reellen isotropen Tangenten, 6 eigentliche Asymptoten, da¬
2
nur
reelle, eigentliche Brennpunkte. Die Kurve besteht ebenfalls aus 2 getrennten
gegen
die
aber
Sie tragen
Ästen,
gegen den eigentlichen Mittelpunkt konvex gekrümmt sind.
4 absolute
2
zugängliche Scheitelpunkte. Die uneigentliche Achse
eigentlichen Mittelpunkt 2 Scheiteltangenten gehen.
wird
geschnitten,
so
daß durch
den
1
jetzt gegebenen Einteilungen sind unvollständig. In der Scheben'schen Arbeit ist überdies
Brennpunkte der einteiligen hyperbolischen Parabel fälschlicherweise die Zahl 3 angegeben,
tatsächlich nur ein reeller, nichtabsoluter Brennpunkt existiert.
Alle bis
für die Zahl der
während
8
uneigentliche konvexe Ellipse.
6. Die
—
k2 a3S > an > 0 > aM oder alt > 0 > a.2S >
liegt ganz
isotrope Tangenten.
Brennpunkte vor.
Die Kurve
—
fc2 a33.
uneigentlichen Gebiet, besitzt keine absoluten Punkte, hat
uneigentliche Asymptoten und 6 uneigentliche
im
Es kommen 2
aber 4
Semihyperbel.
7. Die
eigentlichen Mittelpunkt, dafür eine eigentliche Achse, nur 2 reelle
absolute Punkte, 2 isotrope Tangenten, 2 reelle Asymptoten, wovon eine eigentlich, die
andere uneigentlich. Sie besitzt einen einzigen zugänglichen Ast mit einem Scheitelpunkt.
Wählen wir die eigentliche Achse und die Tangente im eigentlichen Scheitel, sowie die
absolute Polare des Scheitelpunktes zum Koordinatendreieck, so kann die Gleichung der
Semihyperbel auf die Form gebracht werden:
Dieselbe hat keinen
kxx
spezielle
Form der
Gleichung
Es ist
Xj2 -\- k2
aM
x22
—
2k a13 xx
x„
=
0.
„Scheitelgleichung"
bezeichnet werden.
stellt die
Kurve dar:
Semihyperbel
folgende
parabolische Hyperbel.
8. Die
Ihre
k2 an
könnte als
Gleichungsform
Diese
Eine
=
eine
lautet:
Semihyperbel,
deren
Scheitelpunkte orthogonale
Punkte
der Achse sind.
Tangente in einem Scheitel ist daher die absolute Polare des andern Scheitelpunktes.
übrigen gilt auch für diese Kurve, was über die gewöhnliche Semihyperbel gesagt ist.
Die Gleichung und die in § 1 des III. Teiles dieser Arbeit abgeleiteten Eigenschaften zeigen
die nahe Beziehung dieser Kurve zur Euklidischen Parabel.
Die
Im
II. A. Parabeln mit
auf die Form
gebracht
kxx
wo
#2
punkt
ptote
—
0 die
=
eigentlichem Scheitelpunkt.
Die
Gleichung
dieser Kurven kann
werden:
k2 au
x^2 -f-
Je2 a22
x22
—
k an xt x8
=
0,
(a22 > 0)
0 die Scheitelta'ngente darstellt. Der Berührungs¬
eigentliche Achse, x1
zugleich Brennpunkt, seine Tangente stellt eine isotrope Asym¬
=
mit dem A. K. ist
dar.
9. Die
eigentliche elliptische Parabel.
2 «22 > aia > 0.
Die Kurve
liegt
ganz im
nach beiden Seiten hin dem
eigentlichen Gebiet
und besteht
aus
einem
mit dem A. K. zustrebt.
einzigen Ast,
der
Sie besitzt außer
Berührungspunkt
Berührungspunkt keine weiteren absoluten Punkte und außer der Tangente im Be¬
rührungspunkt auch keine weiteren isotropen Tangenten. Es existiert noch eine uneigent¬
liche nichtisotrope reelle Asymptote, die zur Achse normal ist, sowie ein eigentlicher nicht¬
absoluter Brennpunkt auf der Achse.
dem
10. Die
einteilige konkavehy perbolische Parabel. (Zweiteilige Parabel bei Liebmann.)
an > 2 öm > 0.
9
Die Kurve besitzt neben
liche
getrennte absolute Punkte,
isotrope Tangenten, also 3 eigent¬
gleichsinnig parallel und eine zu ihr normal
uneigentliche Brennpunkte, 2 davon auf "der
Berührungspunkt
dem
sowie außer der
Berührungstangente
Asymptoten, von denen 2 zur
noch 2
noch zwei weitere
Achse
stehen, und ebenso 3 nichtabsolute, aber
isotropen Tangente des Berührungspunktes, einen auf der Achse. Sie besteht innerhalb
des eigentlichen Gebietes aus einem einzigen Kurvenast, welcher die beiden getrennten
absoluten Punkte verbindet und dem Berührungspunkt die konkave Seite zuwendet.
11. Die
einteilige
"konvexe
mit äußerem Ende bei
hyperbolische
Liebmann.)
(Hyperbolische einteilige
Parabel.
Parabel
an < 0 < 2 a22.
getrennte absolute Punkte, aber keine weiteren isotropen Tangenten.
eigentlichen Asymptoten ist also 3 wie im vorigen Fall; dagegen existiert
Sie hat ebenfalls 2
Die Zahl der
nur
falls
den
nur
aus
Brennpunkt auf der
getrennten
gekrümmt ist.
einem Ast zwischen den beiden
Die Kurve besteht
gleich¬
absoluten Punkten, der aber gegen
Berührungspunkt
konvex
B. Parabeln mit
uneigentlichem Scheitelpunkt. Als Koordinatensystem
wählen wir: die
eigentliche
absolute Polare.
Achse, die Tangente
Die
Achse.
nichtabsoluter
eigentlicher
ein
Gleichung
im
uneigentlichen Scheitelpunkt
und dessen
heißt dann:
Kxx
12. Die
=
k
ass xs -f- k a3S xx x&
ß2a #2
uneigentliche
konkave
liegt
13. Die
ganz im
uneigentliche
>2aH>
(os22
j>
U).
0.
Uneigentlichen, entspricht
konvexe
U,
elliptische Parabel.
aS3
Die Kurve
=
im
elliptische Parabel.
übrigen vollständig
(Fehlt
bei G.
der Kurve 9.
Scheben.)
2 a22 > 0 > aiS.
uneigentlichen Gebietes, somit ohne absolute Punkte.
Daher existiert noch eine uneigentliche
Sie besitzt aber 2 weitere isotrope Tangenten.
nichtabsolute Asymptote, sowie 3 uneigentliche nichtabsolute Brennpunkte.
Es ist ebenfalls eine Kurve des
14. Die
zweiteilige konkave hyperbolische Parabel.
mit innerem Ende bei
(Hyperbolische einteilige
Parabel
Liebmann.)
2 a22 > a33 > 0.
Diese Kurve besitzt 2 weitere absolute Punkte und 2 weitere
Kurve 10,
also auch 3
besteht im
Eigentlichen
eigentliche Asymptoten
aus
2
getrennten Ästen,
und
die
isotrope Tangenten, wie
Sie
3 uneigentliche Brennpunkte.
beide nach dem Berührungspunkt
hinstreben.
eigentlichem Mittelpunkt. Der Mittelpunkt ist der einzige
Seine Gleichung lautet:
absolute Polare die einzige Asymptote.
k2 an X,2 + k* on xj -\- ai3 xs2
kxx
°» (an > °)-
III. A. Kreise mit
punkt,
seine
=
=
15. Der
imaginäre
Brenn¬
Kreis.
«11 > 0 >
—
«33-
Die Kurve enthält keine reellen Punkte.
2
10
16. Der
eigentliche
Kreis.
«11 >
Die Kurve
liegt
17. Der
Gebiet.
eigentlichen
ganz im
«38 > °-
—
uneigentliche Kreis.
«33 > «11 > °-
—
Die Kurve besteht
aus
Punkten.
uneigentlichen
lauter
JB. Kreise mit eigentlicher Achse.
(Abstandslinien, Gleitkurven.) Die Achse ist eine
eigentliche Asymptote. Alle Kurven dieser Art berühren den A. K. in den Enden der Achse.
Die Gleichung lautet:
Texx
18. Die
k2 au
=
x^ -f-
Je2
a.,„
xj
an
—
xs2
(an > 0).
0,
—
Äbstandslinie.
eigentliche
«•22 > «11 > 0.
Die Kurve besteht
zwei
aus
Ästen, die,
Berührungspunkten streben,
nach den
19. Die
uneigentliche
zur
liegt
und
Achse
ganz im
symmetrisch,
Eigentlichen.
nach beiden Seiten
Abstandslinie.
«11 > «22 > 0-
Gleich wie
vorhin;
Fällen wird die Kurve
nur
liegt
allen
von
vollständig im Uneigentlichen. In diesen beiden
eigentlichen Achsenloten geschnitten, nicht aber von den
die Kurve
uneigentlichen.
20. Die Gleitkurve.
(Enveloppe
stanten reellen Winkel
aller
Geraden, welche mit der Achse einen kon¬
bilden.)
«11 > 0 > «22-
Wie bei 18 und 19.
Berührungssehne
Gleichung
Jcxx
liegt
uneigentliche Achse,
die
im ferneren wie 20 ganz im
=
dieser Kurve kann in der Form
k2 «h
#i2 +
Die Kurve besteht
aus
punkt hinstrebt, anderseits
eine reelle
V. Die
=
k2 «n
#22
einem
zum
nicht aber die
zur
Uneigentlichen.
«u
xs* 4"
einzigen Ast,
2 k2 a12 xt #2
werden:
—
der einerseits
2 k a12 x% xs
zum
und einen
=
0.
absoluten Oskulations-
Sie besitzt stets
uneigentlichen Brennpunkt.
reellen
(Semi¬
Liebmann.)
Gleichung
der Grenzkreise kann
k2
k2 an x2 -f
-g-
22. Der
—
gegeben
einfachen absoluten Punkt sich wendet.
eigentliche Asymptote
zirkuläre Parabel bei
kxx
Kurve trifft
21. Die oskulierende Parabel.
IV.
Die
Die
senkrechte Achse,
(an + a22) x2
—
geschrieben
aä2
xs2
—
k
(an
werden:
—
a22)
xt xa
=
0
(au > 0).
eigentliche Grenzkreis.
«11 > «22 > 0-
Die Kurve enthält
ist der
eigentliche Punkte. Der absolute Berührungspunkt
Tangente die einzige Asymptote.
einzige Brennpunkt,
nur
seine
3.
Ordnung
11
23. Der
uneigentliche
Grenzkreis.
vorigen Fall, aber die Kurve besteht aus lauter uneigentlichen Punkten.
Vom Standpunkt eines hyperbolischen Wesens aus sind die Kurven 1—6 als Mittel¬
punktskegelschnitte anzusprechen, das sind Kegelschnitte mit reellem eigentlichem Mittel¬
punkt. In Bezug auf die abzuleitenden Eigenschaften und Konstruktionen sind die Formen 1
all gemeine", alle folgenden dagegen als »spezielle" Kegelschnitte zu betrachten.
bis 7 als
In diesem Sinne sind die folgenden Untersuchungen geteilt in solche über allgemeine und
solche über spezielle Kegelschnitte. Wir beschränken uns übrigens auf Kurven vom Typus I,
Gleich wie im
„
II und
IV, da die Eigenschaften der Kreise, Abstandslinien und Grenzkreise bereits vielfach
untersucht sind.
5.
§
Gemeinsame Definition und einige
Definition :
Der
geometrische
Ort aller Punkte, die
Abstand haben, ist ein
Hiebei ist
zu
allgemeine Sätze
von
zwei
über
Kegelschnitte.
Kreisen
gegebenen
gleichen
Kegelschnitt.1
bemerken, daß nicht bloß alle eigentlichen und uneigentlichen Kreise,
Abstandslinien und Grenzkreise, sondern auch Punkt und Gerade als Grenzfälle des Kreises
Alsdann umfaßt diese Definition alle überhaupt möglichen
diesen Begriff fallen.
unter
Kegelschnittformen,
Auf Grund des
in der
Euklidischen, wie in
Dualitätsprinzips gelangen
der Nicht-Euklidischen Geometrie.
wir noch
Definition : Die Umhüllung aller Geraden, die
haben, ist ein Kegelschnitt.
Die
Allgemeinheit
dieser Definitionen
nicht im Sinne dieser Arbeit.
von
allgemeinen
gleichen
Abstand
liegt auch
Musterbeispiele:
einige wenige
von zwei sich umschließenden Kreisen gleichen
beiden Kreismittelpunkte zu Brennpunkten hat.
nachzuweisen,
geometrische Ort aller Punkte, die
haben, ist eine Ellipse, welche die
Die Ellipse wird auch umhüllt von allen Geraden, die
Der
einer zweiten
zwei festen Kreisen
würde
zu
weit führen,
Fälle als
Wir erwähnen
Abstand
Kreisen
zu
von
zwei sich umschließenden
Abstand haben.
un¬
gleichen
eigentlichen
Der geometrische Ort aller Punkte, die von einer Abstandslinie und einer Parallelen
deren Achse gleich weit entfernt sind, ist eine ein- oder zweiteilige konkave hyper¬
zu
bolische Parabel, welche die Achse der Abstandslinie und die gegebene Gerade zu Brenn¬
geraden hat.
Der geometrische Ort aller Punkte, die von einem Grenzkreis und einem außerhalb
desselben liegenden Punkte gleichen Abstand haben, ist eine einteilige konvexe hyper¬
bolische Parabel, welche den durch den gegebenen Punkt gehenden Grenzkreisdurchmesser
zur Achse, den gegebenen Punkt zum Brennpunkt hat.
Hieraus ergeben sich sofort Punkt- und Tangentenkonstruktionen der verschiedenen
Kegelschnitte.
1
H. Liebmann: Nicht-Euklidische Geometrie.
(Sammlung Schubert.)
12
Aus den Arbeiten
wir
Story,1 Killing,2 d' Ovidio,8 Liebmann,4 Gertr. Scheben5 erwähnen
vorliegenden Gegenstand beziehende Sätze:
einige allgemeine,
1. Für jeden Punkt eines Kegelschnittes ist die Summe oder Differenz der Abstände
von den beiden Brennpunkten, resp. den beiden Brenngeraden eines Paares konstant.
2. Die Tangente eines Punktes eines Kegelschnittes bildet mit den Brennstrahlen des¬
selben nach einem Paar von Brennpunkten gleiche Winkel.
3. Spiegelt man einen Brennpunkt an allen Tangenten eines Kegelschnittes, so liegen
die Spiegelpunkte auf einem Kreis um den zugeordneten Brennpunkt, dessen Radius
gleich ist dem Abstand der beiden auf der Achse der beiden Brennpunkte liegenden
von
sich auf den
Scheitelpunkte.
4. Für
eines
Kegelschnittes ist die Summe oder Differenz der Winkel,
zusammengehörigen Asymptoten bildet, konstant.
Oder für uneigentliche Asymptotenschnittpunkte:
5. Die Summe oder Differenz der Abstände einer Tangente eines Kegelschnittes von
zwei zusammengehörigen Asymptoten bezw. Asymptotenpunkten ist konstant.
6. Der Berührungspunkt einer Tangente ist gleich weit entfernt von den beiden
Schnittpunkten der Tangente mit einem Paar von Asymptoten.
7. Spiegelt man eine Asymptote an allen Punkten eines Kegelschnittes, so umhüllen
die Spiegelbilder einen Kreis, welcher die zugeordnete Asymptote zur Achse, den
ihr entsprechenden Asymptotenpunkt also zum Mittelpunkt hat, und dessen Radius
gleich ist der Entfernung der beiden Scheitelpunkte auf der zu beiden Asymptoten
senkrechten Achse des Kegelschnittes.
jede Tangente
welche dieselbe mit zwei
II. TEIL.
Sätze und Konstruktionen für
§
1.
Das nomothetische
Wir bezeichnen als Büschel homothetischer
allgemeine Kegelschnitte.
Kegelschnittbüschel.
Kegelschnitte
ein
System
Kegelschnitten
gemeinsamen Asymptoten,
Bezogen auf das
gemeinsame Polardreieck als Koordinatendreieck können das absolute Gebilde w und ein
beliebig gegebener Mittelpunktskegelschnitt Je durch die Gleichungen gegeben werden:
von
also mit denselben 4 absoluten Punkten.
mit
Jcxx
(1)
(2)
iäxx
=
=
an
WxS + Wx22-
xt2 -f-
a22
xj
+ «33
•
Story : On Non-Euklidean Properties of Conies. Americ. Journ. of Mathematics. Vol. V. 1882.
Killing: Die Nicht-Euklidischen Kaumformen in analytischer Behandlung. 1885.
*
d' Ovidio : Le proprietà focali délie coniche nella metrica proiettiva. Atti délia Accademia di Torino.
Sulle coniche confocali nella metrica proiettiva. Daselbst. Teoremi sulle coniche nella
1890—91.
26.
metrica proiettiva. Daselbst.
1
W. E.
J
W.
4
H. Liebmann
8
G. Scheben: a.a.O. S. 10.
:
a. a.
0. S. 19.
13
Alle
durch
(3)
Kegelschnitte,
eine Gleichung:
fex
-
Xwxx
die mit h ein homothetisches Büschel bilden, lassen sich darstellen
(flu
=
-
Die Discriminante dieser
(4)
D
(X)
fc2
X)
x*
Gleichung
=
(an
-
Geradenpaar
(")
und hieraus die
zerfällt:
fc»
X) x* + (a33 + X) x*
(a,,
von
-
*»
X) (ass + X).
Xj
=
Gleichungen
Xj
h y «u
alt
—
—
«s»
a22
=jg—, X3
=
der 3 Paare
(7j„, Ti„') : h\
(7t8, /ig'):
Tg—>
=
0.
X, für welche der betreffende Kegelschnitt in
.
(hv h,1) :
(6)
-
ist:
F X)
Ihr Verschwinden liefert die "Werte
ein
+ (a22
•
•
V«u + £2 «83
von
x2 ±
x1
•
=
—
a3S.
Asymptoten:
V ffljj -j- h2 aS3
+ \
*i ±
—
V
a22
—
—
«22
>
xs
fc2 ag3
—
•
& aS3
=
a;3
•
0
=
x2
0
=
0
14
Damit alle
Asymptoten
reell werden,
etwa an > a22 voraussetzen,
die
Büschels sind in
Ist
§
—
und
hinreichend, daß,
wenn
wir
7c2a33>a22
4 des ersten Teiles
diesem Fall
notwendig
Bedingung
an >
erfüllt sei, wie auch in
ist
eigentliche
angegeben
Sämtliche
ist.
konkave oder konvexe
Kegelschnitte des
Hyperbeln (siehe Fig. 1).
dagegen
^11 '-> ß22 -^
^33!
eigentlichen Ellipsen und uneigentlichen Ellipsen.
uneigentliche Asymptoten h und h' (siehe Fig. 2).
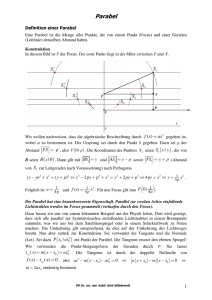
Da ein Kegelschnitt durch 5 Punkte bestimmt ist, gilt der
Satz 1 : Durch jeden Punkt der Ebene geht ein und nur ein Kegelschnitt eines homoOder anders ausgedrückt: Durch jeden Punkt der Ebene geht ein
thetischen Büschels.
einziger Kegelschnitt, der mit einem gegebenen die Asymptoten gemeinsam hat.
Jede Gerade in der Ebene, die nicht durch einen der vier absoluten Punkte geht, wird
den Kegelschnitten des homothetischen Büschels in Punktepaaren einer Involution
von
geschnitten, deren Doppelpunkte diejenigen Punkte der Geraden sind, in welchen dieselbe
Die Enden der Geraden gehören
zwei Kegelschnitten des Büschels berührt wird.
von
so
besteht das homothetische Büschel
Es existieren dann
nur
2
reelle,
aus
aber
'
15
ebenfalls der Involution
Sie
sind
aber
nur
an;
die beiden
reell,
dann
wenn
Berührungspunkte
die
Involution
der
sind somit
orthogonale
Schnittpunkte
auf
Punkte.
der Geraden
Schnittpunktepaare sich nicht trennen, also wenn zu beiden
je
gerade Anzahl von absoluten Punkten des Büschels sich befindet
die
eine
Gerade
oder wenn
gerade Anzahl von Asymptoten im Eigentlichen schneidet.
Liegen z. B. alle 4 absoluten Punkte des Büschels bezüglich der Geraden auf gleicher
Seite, so wird dieselbe von 2 konkaven Hyperbeln berührt. Liegen dagegen 2 absolute
hyperbolisch ist,
d. h.
Seiten der Geraden
Punkte auf der
wenn
die
eine
einen, die beiden
die Gerade.
andern auf der andern Seite der
Im
Geraden,
ersten Fall trifft die Gerade keine der
Hyperbeln
eigentlichen Gebiet, im letzten Falle hingegen werden
geschnitten. Sind die absoluten Punkte sämtlich imaginär,
2 konvexe
im
4
Asymptoten
so
im
so
berühren
Asymptoten
Eigentlichen
existieren zwei reelle, aber
von einer eigentlichen
die
welche
Ellipse,
Asymptotenpunkte
gemeinsam haben.
uneigentlichen
Unter den erwähnten Voraussetzungen gelten die folgenden Sätze:
Satz 2: Irgend zwei Kegelschnitte eines homothetischen Büschels schneiden auf einer
Geraden, die nicht zu einer Asymptote parallel ist, Sehnen mit gemeinsamen Mittelpunkten
heraus. In diesen Punkten wird die Sehne von zwei weiteren Kegelschnitten des Büschels
berührt.
(Vgl. Fig. 1).
Satz 3: Die Strecken zwischen den Schnittpunkten einer beliebigen Sekante mit einem
Kegelschnitt und den Schnittpunkten derselben mit einem Paar von Asymptoten sind gleich
lang.1
Satz 4: Die Schnittpunkte einer beliebigen Geraden mit einem Paar von Asymptoten
eines gegebenen Kegelschnittes sind gleich weit entfernt von den Schnittpunkten der Geraden
mit einem zweiten Asymptotenpaar.
Satz 5: Der Berührungspunkt einer Kegelschnittstangente halbiert die Strecke zwischen
den Schnittpunkten derselben mit irgend einem Paar von Asymptoten oder mit einem zum
gegebenen homothetischen Kegelschnitt.1
Aufgabe 1: Gegeben ist ein Kegelschnitt durch ein Paar von Asymptoten h, h1 und
Man konstruiere die Tangente in demselben.
einen beliebigen Punkt P.
eine
wir
der gegebenen Asymptoten, z. B. h (siehe Fig. 3) am ge¬
Lösung: Spiegeln
Punkt
die
P, so geht
Tangente t dieses Punktes durch den Schnittpunkt S des
gebenen
Spiegelbildes h mit der zugeordneten Asymptote h'.
Fällt S ins Uneigentliche, so läßt sich an Stelle von S dessen, absolute Polare s*, das
ist das gemeinschaftliche Lot von h und h', verwenden. Dasselbe verbindet auch das Spiegel¬
bild R* des h entsprechenden Asymptotenpunktes R* mit dem zugeordneten Asymptoten¬
punkt R'*, so daß die Konstruktion auch ausführbar ist bei uneigentlichen Asymptoten.
Beschreibt der Punkt P den Kegelschnitt h, so bewegt sich der Spiegelpunkt R* von
Hieraus ist folgende
R* auf einem Kreise um den zugeordneten Asymptotenpunkt R'*.
Konstruktion von Punkten eines Kegelschnitts mit gegebenen Asymptotenpunkteh zu ent¬
nehmen: Um den einen der gegebenen Asymptotenpunkte R*, R'* schlagen wir einen
Kreis mit einem Radius gleich dem gewünschten Abstand der Scheitelpunkte auf der Achse
uneigentliche Asymptoten,
Story: a.a.O.
jede eigentliche Gerade
konvexen
und einer
1
und
S. 12.
wird berührt
16
gegebenen Asymptotenpunkte. Verbinden wir dann den andern Punkt mit den Punkten
des Kreises und halbieren die Verbindungsstrecken, so erhalten wir beliebig viele Punkte
eines Kegelschnittes, welcher die Punkte H*, H'* zu Asymptotenpunkten hat.
Satz 6: Der geometrische Ort des Mittelpunktes der Verbindungsstrecke eines festen
der
Kegelschnittpaar, welches den gegebenen
Zu einer Schar kon¬
zu Asymptotenpunkten hat.
homothetischer Kegelschnitte (siehe Fig. 2).
Punktes mit den Punkten eines Kreises ist ein
Punkt und den
des Kreises
Mittelpunkt
gehört ein
zentrischer Kreise
Büschel
Mittelpunkt der oben genannten Verbindungsstrecke auf den zugehörigen
Kreisradius ist die Tangente an den Kegelschnitt im Mittelpunkt der Verbindungsstrecke.
Aufgabe 1 läßt sich auch lösen mit Hilfe des Pascal'schen Satzes, der ja in der
hyperbolischen Geometrie gleichfalls Gültigkeit besitzt.
Aufgabe 2: Gegeben ist ein Kegelschnitt durch ein Paar von Asymptoten Alt h^ und
Man bestimme den Berührungspunkt derselben.
eine Tangente t.
Satz 5 ist der gesuchte Berührungspunkt P der Mittelpunkt der Strecke
Nach
Lösung :
S S', wenn S, S' die beiden Schnittpunkte der Tangente t mit den gegebenen Asymptoten
Aj, h±' sind (Fig. 4). Sind S, 8' uneigentliche Punkte, so bestimmen wir die gemeinsamen
Lote von t und Alt bezw. von t und At'. Diese Lote s*, s'* mögen die Tangente t in S*, S'*
treffen. Der Berührungspunkt P halbiert auch die Strecke S* S'*. Sind schließlich hv A/
Das Lot
vom
17
uneigentlich, so läßt sich die Konstruktion so durchführen : s* und s'* sind dann die Lote
von den ht, V entsprechenden Asymptotenpunkten H^*, Sx'* auf die gegebene Tangente.
Die Aufgabe besitzt zwei Lösungen, über deren Realität auf Seite 15 das Nähere
gesagt ist.1
'Anmerkung. In der hyperbolischen Geometrie besitzt jede
uneigentlichen, die zueinander orthogonal sind.
zwei
gegebene Gerade
zwei Winkelhalbierende haben.
Die
von
Strecke zwei
Mittelpunkte, einen eigent¬
entspricht dual der Tatsache, daß
Großmann in seiner Programmarbeit 1904
lichen und einen
M.
Dies
der Thurganischen Kantonsschule Frauenfeld über
Geometrie"
Die
gegebenen
Resultate sind im
der beiden Winkelhalbierenden zweier Geraden
Gleichungen
=
iox
W&
(x„ x„ x3)
a
Darin
•
bedeuten
ui
ax
•
Die Koordinaten des
Punkte A
„Die fundamentalen Konstruktionen
angeführten Sinne zu ergänzen:
+
W£
•
bx
0, wx'
=
Wb\
=
•
ax
ax
=
-
0 und bx
Wa\
eigentlichen, bezw. uneigentlichen Mittelpunktes
(*/„ y„ ys) sind:
der
-bx
der nichteuklidischen
=
=
0 lauten
:
0.
Verbindungsstrecke
zweier
und B
=
Qz2
=
Qyy
Xi
•
0 und
+ Qxx
Wg
=
0
yi,
•
die
a
•
aï
=
Gleichungen
Qy\
•
xt
—
des absoluten
ßXx
•
Vi-
Kegelschnitts
in
Punkt-,
bezw.
Linienkoordinaten,
Aus
dem
Vorangehenden ergibt
sich
auch
noch in
einfacher Weise die
Gleichung
des
eigentlichen,
bezw. uneigentlichen Mittellotes:
Qaz
=
Qxx
•
Qy\
±
Qyz
•
ßl
=
0.
3
18
Für Je
=
0
geht
das absolute Gebilde
über in
unendlich ferne Gerade der Euklidischen Ebene.
xs2
=
0, das ist die doppelt gezählte
möglichen reellen Asymptoten
eigentliche Asymptoten existieren für die
Hyperbel; für die Ellipse werden dieselben imaginär.
Das homothetische Büschel wird zu einem Büschel ähnlicher und ähnlich gelegener
Kegelschnitte (Hyperbeln oder Ellipsen). Die Sätze 1—5 gelten sozusagen unverändert,
nämlich mit der Einschränkung, daß jede Gerade nur von einem eigentlichen Kegelschnitt
berührt wird ; als zweiter tritt für jede Gerade die doppelt gezählte unendlich ferne Gerade
auf. Von den Mittelpunkten der Kegelschnittsehnen wird der uneigentliche stets zu einem
Punkt dieser unendlich fernen Geraden.
Aufgabe 2 ist daher eindeutig. Die Lösung der
ist
in
der
Geometrie
Euklidischen
1
dieselbe, wenngleich der geometrische Ort
Aufgabe
der Spiegelbilder einer Asymptote in Bezug auf alle Punkte eines Kegelschnitts sich auf
die beiden unendlich fernen Punkte der beiden Asymptoten reduziert, da diese Spiegelbilder
alle parallel werden. Der geometrische Ort des Mittelpunktes der Verbindungsstrecke eines
festen Punktes mit den Punkten eines gegebenen Kreises wird in der gewöhnlichen Geo¬
metrie zu einem Kreis, der zum gegebenen ähnlich liegt mit dem gegebenen Punkt als
fallen 4 auf die unendlich ferne
Gerade,
nur
Von den 6
2
Ähnlichkeitspunkt.
§
Wir
gehen
2.
Das Dreieck konstanten Inhalts.
Satz 4 in
§
5 des I.
Teiles, den wir noch ergänzen:
Winkel, welche eine Kegelschnittstangente mit
zwei zusammengehörigen Asymptoten bildet, ist konstant, nämlich gleich dem Winkel
aus
von
Satz 7: Die Summe oder Differenz der
zwischen den beiden durch denselben
Mittelpunkt gehenden Scheiteltangenten.1
Tangente t insbesondere mit den beiden Asymptoten ha, h's (siehe
Fig. 4), die durch den eigentlichen Mittelpunkt Og gehen, so hat das Dreieck Os TT, wo
T, T die Schnittpunkte von t mit h3, h\ sind, konstante Winkelsumme, und da in der
hyperbolischen Geometrie der Flächeninhalt dem Winkeldefekt proportional ist, so gilt der
Satz 8: Die Tangente in einem eigentlichen Punkt eines Kegelschnittes bildet mit den
beiden Asymptoten durch den eigentlichen Mittelpunkt ein Dreieck konstanten Inhalts.
Satz 9: Verwandelt man ein Dreieck unter Beibehaltung eines Winkels in andere
inhaltsgleiche Dreiecke, so umhüllt die dem festen Winkel gegenüberliegende Seite einen
Kegelschnitt, der die Schenkel des festen Winkels zu Asymptoten hat. (Für ein eigent¬
liches Dreieck ist dies eine konvexe Hyperbel.)
Ist der Schnittpunkt der beiden Asymptoten uneigentlich, so hat die trapezförmige
Figur, begrenzt durch die Tangente, die beiden Asymptoten und die zu diesen senkrechte
Schneiden wir die
Achse, ebenfalls konstanten Flächeninhalt.
Satz 5 in § 5 des I. Teiles läßt sich gleichfalls vervollständigen :
Satz 10: Die Summe oder Differenz der senkrechten Abstände einer
Tangente von zwei
zusammengehörigen Asymptoten oder Asymptotenpunkten ist konstant, nämlich gleich dem
Abstand der Scheitelpunkte auf der zu beiden Asymptoten senkrechten Achse.
Im Falle
1
Story:
a. a.
0.
S. 12.
i
19
eigentlichem Berührungspunkt die Summe
der beiden Asymptoten Endpunkte
verschiedener Kurvenäste oder solche desselben Astes des eigentlichen Gebietes verbinden.
Für eine Tangente mit uneigentlichem Berührungspunkt ist es gerade umgekehrt.
eigentlicher Asymptoten
ist für eine
oder Differenz der Abstände
Tangente
mit
konstant, je nachdem jede
Fällt der Punkt auf einen der absoluten Punkte des
Kegelschnitts,
so
ergibt
sich
aus
Satz 7 und 10:
Satz 11: Die
Tangente in einem Endpunkt einer Asymptote bildet mit der zugehörigen
Asymptote einen Winkel gleich dem Winkel der beiden Scheiteltangenten durch
den gleichen Mittelpunkt.
Schneidet die Tangente die Asymptote im Uneigentlichen, so
ist der senkrechte Abstand zwischen Tangente und Asymptote gleich der Entfernung der
Scheitelpunkte auf der zur Asymptote senkrechten Achse (siehe Fig. 5).
andern
Es
ergeben sich
Satz 12: Alle
stände
von
noch
folgende
Ortssätze:
Geraden, für welche die Summe oder Differenz ihrer senkrechten Ab¬
zwei festen Geraden konstant
mit den beiden Geraden als
Asymptoten.
ist,
umhüllen eine konkave oder konvexe
Hyperbel
20
Geraden, für welche die Summe oder Differenz
Satz 13: Alle
festen Punkten konstant ist,
umhüllen eine
der Abstände
zwei
von
welche die beiden
Punkte
Ellipse,
gegebenen
Asymptotenpunkten hat (siehe Fig. 2).
Aufgabe 3: Ein Kegelschnitt ist bestimmt durch ein Paar von Asymptoten h2, 7»2' und
einen beliebigen Punkt.
Man konstruiere die Scheitelpunkte, bezw. die Scheiteltangenten
durch den eigentlichen Mittelpunkt.
(Vgl. Fig. 5.)
Lösung: Da vom Kegelschnitt 5 Punkte gegeben sind, so können wir mit Hufe des
zu
Pascal'schen Satzes
;
Endpunkt
gente
t
Tangente t in einem absoluten Punkt der Kurve z. B.
gegebenen Asymptote h2 bestimmen. Der senkrechte Abstand
W der
die
der nicht durch ihren
von
Berührungspunkt gehenden Asymptote h^'
ist
im
einen
der Tan¬
gleich
dem
Abstand 2 a^ der Scheitel auf der zu beiden Asymptoten senkrechten Achse.
Ermitteln
wir als gemeinschaftliche Parallelen zu den gegebenen Asymptoten diejenigen durch den
eigentlichen Mittelpunkt, und schneiden wir die Tangente t mit einer derselben in einem
eigentlichen Punkt, so ist der zwischen Tangente und Asymptote liegende Winkel gleich
dem Winkel 2 <J>3 der durch den eigentlichen Mittelpunkt gehenden Scheiteltangenten.
Die Aufgabe ist auch lösbar mit Hilfe der Polinvolutionen auf den Achsen, deren
Doppelpunkte die gesuchten Scheitelpunkte sind.
Satz 7—9 sind bekannt in der Euklidischen Geometrie.
Satz 10 dagegen verliert
seinen Sinn, da die in Frage kommenden Asymptoten und Asymptotenpunkte auf die un¬
endlich ferne Gerade fallen.
Satz 11 wird selbstverständlich, da die Tangenten in den
absoluten Punkten paarweise mit den Asymptoten und Scheiteltangenten durch den eigent¬
lichen Mittelpunkt zusammenfallen.
§ 3.
Satz 14: Verbindet
Punkten
von
desselben,
konstanter
Die konstante
man
einen variablen Punkt eines
schneiden diese
so
Länge heraus.1
ergibt sich aus
Der Beweis
vom
Asymptotenstrecke.
Verbindungslinien
Doppelverhältnisses der vier Strahlen
gegebenen Punkten und nach den Enden der
der Konstanz
veränderlichen Punkt nach den beiden
Kegelschnittes mit zwei festen
Asymptote eine Strecke
auf einer
des
Asymptote.
Lassen wir
zusammenfallen,
den
so
variablen Punkt nacheinander mit
folgt
Schneidet
Satz 15:
jedem
der beiden festen Punkte
der
man
eine
Asymptote
mit
den
beiden
Tangenten,
die
von
einem
beliebigen
Kegelschnitt gezogen werden können, so wird die Strecke
zwischen den beiden Schnittpunkten halbiert durch die Berührungssehne (siehe Fig. 6).
Punkt der Ebene
an
den
Sind die beiden festen Punkte absolute Punkte,
Zieht
Satz 16:
Parallelen
Strecke
1
zu
von
Story:
einer
man
Asymptote,
Länge
konstanter
a. a.
0.
S. 12.
so
so
der
gilt
durch einen variablen Punkt eines
Kegelschnittes die beidseitigen
zugeordneten Asymptote eine
schneiden dieselben auf der
heraus
(Fig. 7).
21
eine gegebene Strecke auf einer Geraden, so ist der geo¬
man
Schnittpunktes der Verbindungslinien ihrer Endpunkte mit zwei festen
Punkten ein Paar von Kegelschnitten, die durch die beiden festen Punkte hindurch gehen
und die gegebene Gerade zur Asymptote haben.
Satz 18: Verschiebt man eine konstante Strecke auf einer von zwei gegebenen Geraden
und zieht man durch die Streckenendpunkte nach verschiedenen Seiten die Parallelen zur
zweiten Geraden, so ist der geometrische Ort des Schnittpunktes ein Paar von Kegel¬
Satz 17:
Verschiebt
metrische Ort des
schnitten, für welche die beiden gegebenen Geraden ein gemeinsames Asymptotenpaar dar¬
stellen.
Die
orthogonal zu
Brenngeraden.
zu
Asymptoten homologen Brennpunkte
Brennpunkten des andern, liegen also
den
den
Es seien
des einen
Kegelschnittes
auf den diesen
sind
entsprechenden
(siehe Fig. 7) A und B die Endpunkte der konstanten Strecke auf einer
Asymptote
hl, AW" und BW", bezw. AW' und J3TP" die beiden Paare von
Parallelen zur zugeordneten Asymptote TP" W"
hx', P bezw. P je ein Punkt der beiden
Kegelschnitte. Das vollständige Viereck AP BP besitzt eine feste Diagonale W"W",
welche vom Gegenseitenpaar A 2?= 7^, PP in 2 Punkten geschnitten wird, die zu TP", TP"'
Von diesen beiden Schnittpunkten ist aber der eine 013 der absolute
harmonisch liegen.
WW
=
=
22
Pol
von
ov ebenfalls fest.
Es muß also auch PP stets
durch denselben
Punkt
D,
den
P, P,
Schnittpunkt
h^
gehen.
Lage der konstanten Strecke AB hervorgehen, liegen also stets so, daß ihre Verbindungs¬
linie durch ,den Schnittpunkt der zugeordneten Asymptote mit der zu ihr senkrechten Achse
hindurch geht. Die Punkte P, P, 0, D, wo C der Schnittpunkt von PP mit \ ist, bilden
ebenfalls eine harmonische Gruppe.
Dasselbe gilt von den Punkten A, B, C, Oj.
Die
in
und
P
treffen
P
sich
auf
Tangenten
hv
Die beiden Punkte
und ot
von
Fig.7.
Bewegt
Je, k:
einer bestimmten
'
Kegelschnitte
k und
k,
die
der andern mit der
zu
Asymptote, so beschreiben die
hervorgehen durch eine
Asymptoten Kollineationsachse, der
auseinander
involutorische Kollineation, wobei die eine der beiden
Es seien
aus
sich die konstante Strecke AB also auf einer
Punkte P und P zwei
Schnittpunkt
die
beiden senkrechten Achse Kollineationszentrum ist.
S, S zwei einander im angegebenen Sinn entsprechende Scheitelpunkte von
Die Tangenten s, s in 8, 8 bilden mit \, \' ein harmonisches Strahlenbüschel. Eine
nun
durch
Os gehende Asymptote h3 wird von demselben in einer harmonischen Punktgruppe
T, T, W, W" geschnitten. Nun ist aber, wie in § 6 gezeigt wird, OsT= OsF1 und
03T= 03F1, ffofj, F} die zu hx homologen Brennpunkte von Je, bezw. k auf o1 sind.
Sind V, V die absoluten Punkte von o±, so sind die Punkte F±, Flf V, V ebenfalls har¬
monische Punkte,
w. z.
b.
w.
23
Ändert
Länge
Kegelschnitte.
die
man
homothetischer
Wählen wir für die festen Punkte in
eigentlichen Achse,
Strecke,
der konstanten
so
ergibt
Satz 14 ein Paar
sich ein ganzes Büschel
von
Scheitelpunkten
und lassen wir den veränderlichen Punkt mit einem derselben
einer
zusammen¬
Verbindungslinien die Achse und eine Scheiteltangente. Sie
schneiden eine der beiden Asymptoten durch Os im eigentlichen Mittelpunkt und einem
Punkt, dessen Entfernung von 0a nach dem Obengesagten der Entfernung der Brennpunkte
auf der Achse der Scheitelpunkte vom Mittelpunkt gleich ist.
Satz 19: Verbinden wir einen beliebigen Punkt eines Kegelschnittes mit den beiden
Scheitelpunkten einer eigentlichen Achse, so schneiden diese Verbindungslinien auf einer
Asymptote durch den eigentlichen Mittelpunkt eine Strecke gleich dem halben Abstand
fallen,
so
als
ergeben sich
der beiden Brennpunkte dieser Achse heraus.
Schneiden wir aber dieselben
Verbindungslinien
mit einer
der variable
zur
genannten Achse
Punkt mit
einem
senk¬
Scheitel
zu¬
Asymptote, so ergeben sich, wenn
sammenfällt, als Schnittpunkte der Verbindungsgeraden der beiden Scheitel und der Tangente
Hieraus ist zu entnehmen:
im einen Scheitel zwei orthogonale Punkte.
Satz 20: Verbindet man einen beliebigen Punkt eines Kegelschnittes mit den beiden
Scheitelpunkten einer eigentlichen Achse, so treffen diese Verbindungslinien eine der beiden
zur Achse normalen Asymptoten in zwei orthogonalen Punkten, oder anders ausgedrückt:
die Verbindung mit dem der Asymptote näher liegenden Scheitel steht senkrecht auf dem
Lot zur Asymptote, das man im Schnittpunkt der Verbindungslinie nach dem entfernteren
rechten
Scheitel errichten kann.
Berührungssehne, wenn die Tangenten von einem
Punkt an einen Kegelschnitt gegeben sind (siehe Fig. 6).
Die Sätze 14, 15, 17, 19 gelten auch in der Euklidischen Geometrie. Satz 16 und 18
hingegen verlieren ihre Bedeutung, indem die dort genannten Parallelen in der Euklidischen
Geometrie identisch werden, desgleichen Satz 20, da die Asymptoten mit dem absoluten
Satz 15 liefert eine Konstraktion der
Gebilde zusammenfallen.
§
4.
Die Schar konfokaler
Kegelschnitte.
'
Kegelschnitte ein System von Kegelschnitten mit
gemeinsame Polardreieck des A. K. w
gemeinsamen Brennpunkten.
und des beliebigen Kegelschnittes Je als Koordinatensystem wählen, so ergeben sich die
Gleichungen des A. K. und des Kegelschnittes Je in Linienkoordinaten :
Wir bezeichnen als Schar konfokaler
Wenn wir wieder das
(i)
ûK
(2)
%
o,
ç1»+y-A«ç,»
Än tf + A„ & -r A33 &
=
=
=
•
=
0,
wo
-"11
gesetzt ist.
Alle
stellen durch die
(3)
ZK
=:
K22 °3S'
Kegelschnitte
Gleichung:
-
X
%
=
(A„
""-22
==
ö33 ßll>
der konfokalen
-
X) Ç,« + (A„
-"83
r=
ail ß22
Schar, welche Je enthält, lassen sich dar¬
-
X) ?2* + (^33 + Ä« X) &
=
0
24
Aus der Diskriminante
(4)
der
D
Gleichung
Paar
von
3
ergeben
(X)
(5)
folgen
daraus die
-
X) {A22
—
X2
A^i
Gleichungen
V
Damit alle
Bedingungen
—
Brennpunkte
¥
Brennpunktepaare
^l!!2i
X3
+
-
X)
Kegelschnitt
der betreffende
in ein
zerfällt:
_4
=
von
p
Brennpunkten:
y/-WAn-A~. Ç,
=
V*»Ae + 4»- ç,
o,
=
ç1-Va»^m + 4„.çï
0,
=
o.
werden, ist notwendig und hinreichend, daß eine
der
erfüllt sei:
—
A
Atl ^> Ass ~^>
—
k
Ai2>
Die Schar enthält in diesem Fall als
nebst
X) {Asz +
der 3 Paare
PA
reell
3
=
y/AM-An- Ç,
V^-^2- 5i
(6)
-
X, für welche
gemeinsamen
Xa
Es
(An
sich die Werte
eben die
Punkten,
=*=
uneigentlichen
konvexen
Ellipsen.
oder
—
k
Ai2
s>
Ass ^>
—
k
A±1.
Hyperbeln
eigentliche Kegelschnitte
Alle Brennpunkte sind uneigentlich (siehe Fig. 8).
lauter konkave
25
Ist
dagegen
—
so
Die
werden
B.
z.
k*
Alx
zwei
nur
—
fc2
A22 > Aas,
oder
Brennpunkte (diejenigen
Schar konfokaler
uneigentlichen
>
Kegelschnitte
besteht
Gebietes und konvexen
Ass
auf
aus
>
—
h2AM>
ox) reell,
konkaven
Je2
—
An,
eigentliche Punkte.
Ellipsen des eigentlichen und
dafür aber
Hyperbeln (siehe Fig. 9).
Es
gelten die folgenden Sätze:
Irgend ein Kegelschnitt der konfokalen Schar ist bestimmt, wenn eine Gerade
als Tangente gegeben ist, oder: Es existiert ein einziger Kegelschnitt, der mit einem
ge¬
gebenen die Brennpunkte gemeinsam hat und überdies eine gegebene Gerade berührt.1
Satz 22: Durch jeden Punkt der Ebene gehen zwei konfokale
Kegelschnitte, dieselben
Satz 21:
schneiden sich in
gegebenen
einem Paar
von
Satz 23:
konfokale
diesem Punkte
rechtwinklig.
Die
dieser
Kegelschnitte im
irgend
Brennpunkten.1,2
Zieht
man
Kegelschnitte,
einem
von
so
beliebigen
schließen
die
Punkt der Ebene die
beiden
Winkel ein.
1
Tangenten
Punkt sind die Winkelhalbierenden der Brennstrahlen des Punktes nach
d' Ovidio
:
a. a.
0.
S. 12.
2
Story:
a. a.
0.
Tangentenpaare
Tangenten
miteinander
an
zwei
gleiche
S. 12.
4
26
Die
Satz 24:
Tangenten
den Brennstrahlen
mit
von
der Ebene
einem Punkt
des Punktes
einen
an
einem Paar
irgend
nach
bilden
Kegelschnitt
zusammengehöriger
Brenn¬
punkte gleiche Winkel.1
Verbinden wir einen
Satz 25:
bilden
so
Paar
Verbindungslmien
die
Punkt mit zwei Paaren
beliebigen
nach
einen Paar mit
dem
von
Brennpunkten,
denjenigen
nach dem andern
Kegelschnittes
sind die Winkel¬
Winkel.
gleiche
Satz 26:
Tangente
und Normale eines Punktes eines
halbierenden der Brennstrahlen des Punktes nach irgend einem Paar von Brennpunkten.1
Aufgabe 4: Ein Kegelschnitt ist gegeben durch ein Paar von Brennpunkten und eine
beliebige Tangente. Man bestimme den Berührungspunkt.
Lösung: Wir spiegeln den einen der beiden Brennpunkte an der gegebeneu Tangente,
verbinden den Spiegelpunkt F' von F' mit dem andern Brennpunkt F (siehe Fig. 10). Der
Schnittpunkt der Verbindung F'F mit der gegebenen Tangente ist der gesuchte Berührungs¬
punkt T.
Sind die Brennpunkte uneigentlich, so spiegeln wir die eine von zwei zusammen¬
gehörigen Brenngeraden, z. B. f* an der Tangente t. f* ist die absolute Polare von F
und die Gerade F'F ist gemeinschaftliches Lot von f* und f*.
Eine andere Lösung der Aufgabe ergibt sich im Falle uneigentlicher Brennpunkte auf
Grund des Brianchon'sches Satzes, der in der hyperbolischen Ebene ebenfalls Gültigkeit besitzt.
Aufgabe 5. Von einem Kegelschnitt ist ein Paar von Brennpunkten und ein beliebiger
Man konstruiere die Tangente in diesem Punkt.
Punkt gegeben.
Lösung: Wir verbinden den Punkt T (siehe Fig. 10) mit den beiden gegebenen Brenn¬
punkten und konstruieren die Winkelhalbierenden der beiden Brennstrahlen. Dieselben
stellen die Tangenten im Punkte T derjenigen beiden Kegelschnitte dar, die nach Satz 22
Wenn wir uns natürlicherweise auf eigentliche Punkte be¬
durch diesen Punkt gehen.
schränken, so ist die Konstruktion immer ausführbar und liefert stets zwei reelle Lösungen.
Bilden wir zu Gleichung (3) eines beliebigen Kegelschnittes der konfokalen Schar die
entsprechende Gleichung in Punktkoordinaten, so können wir dieselbe auf die Form bringen :
•
^}
All
—
X~rA22
—
X~rAts-\-h'iX
Bedeuten xv x2, x3 die Koordinaten eines gegebenen Punktes, so ergibt sich aus (7)
quadratische Gleichung zur Bestimmung des Parameters X, deren Wurzeln die Parameter
derjenigen beiden konfokalen Kegelschnitte sind, die durch den gegebenen Punkt gehen.
Diese beiden Parameterwerte können, genau wie in der Euklidischen Geometrie, als „elliptische
Koordinaten" des Punktes (a;1, xv xa) eingeführt werden. Zwischen diesen beiden Parameter¬
werten Xj, X2 und den Koordinaten xlf #2, xs bestehen die Beziehungen:
eine
,q\
r_
t
Al ~~T
\°)
y
/q\
1
Story:
^
vc
A2
-Aiz
—
-^as) xi ~\('c -^-n
•
T.2
hi
&lt aM fl33 Vffill Xl
y
a. a.
0.
S. 12.
J,x
2
~T"
1
-f-
-"-83)
—
T.2
K
fl22 X2
r
2
X2
~1~
(•"«
^2
r
~r
-"-22) xs
Pxx
2
„,
Wxx
U,g
a33 ^3
)
-^
.
fex)
*
&XX
27
Hieraus
ergeben
sich
zur
Berechnung
der %t
aus
gegebenen Wertepaaren \, X2
die
inversen Formeln:
(10)
Aus 8
p
•
z*
=
(4,3 +
W
AM) \AU*
p
•
x*
=
(^S8 +
£2
A1X) [A^J
p
•
V
=
C422
^i) [Ass*
folgt,
daß für pxx
—
=
0
Xj -j- X3
—
—
-
Aa (Xt
X2) + \
•
Xs]
-
A„ (X, -f X2) + Xx
•
X2]
+
^88 (X! -f X3) + Xi
0
wird, d. h.
pxx
•
=
X2]
0 ist
der
geometrische
Punkte, für die die Summe der elliptischen Koordinaten gleich Null ist oder
deren elliptische Koordinaten entgegengesetzt gleich sind. Es ist dies also ein zu Tcxx
0
Ort
aller
=
Kegelschnitt. Er ist der geometrische Ort aller Punkte, von denen an den
gegebenen Kegelschnitt aufeinander senkrechte Tangenten gezogen werden können.1 Er
schneidet den A. K. und den gegebenen Kegelschnitt in den Berührungspunkten derselben
mit ihren gemeinsamen Tangenten, hat also die Brenngeraden des gegebenen Kegelschnittes
zu Asymptoten.
Satz 27: Der geometrische Ort aller Punkte, von denen aus sich an einen gegebenen
Kegelschnitt zueinander senkrechte Tangenten ziehen lassen, ist ein zum gegebenen kon¬
zentrischer Kegelschnitt, welcher die Brenngeraden des gegebenen zu Asymptoten hat.
Seine Gleichung lautet:
konzentrischer
(11)
Pxx
1
=
Qc2 AM
Salmon-Fiedler
:
-
Ass)
x*
+ {¥ An
Analytische Geometrie
der
-
Ass) x2*
Kegelschnitte.
-
(An -f A22)
II. Bd.
x*
=
0.
28
Wenn 7c in ein
erhalten wir den
so
elementargeometrischen
geometrische Ort aller Scheitelpunkte rechter Winkel, deren Schenkel
hindurchgehen, ist ein Kegelschnitt, der diese beiden Punkte zu
Der
Satz 28:
Punktepaar zerfällt,
durch zwei feste Punkte
Asymptotenpunkten besitzt.
Alle zu den Kegelschnitten
elliptischen
Für 1c
daß
Ort aller Punkte
einen konstanten Wert hat.
ihrer
Koordinaten konstant ist, einen
wir
erhalten
0
=
Kegelschnitte p bilden
jeder Kegelschnitt dieses Büschels der
Summe ihrer elliptischen Koordinaten
ergibt sich,
ist, für welche die
Gleichung 9 lehrt, daß alle Punkte,
ein homothetisches Büschel.
geometrische
einer konfokalen Schar kovarianten
Aus 8
absolute
das
zu
für welche das Produkt
Kegelschnitt
k homothetischen
Gebilde
Euklidischen
der
Ebene
in
bilden.
Linien¬
koordinaten :
tf + &
welche
Gleichung
hier
übrig
Satz
von
konjugiert imaginärer Kreispunkte der unendlich fernen Geraden
dasselbe als nicht spezialisierte Klassenkurve aufzufassen ist, gelten
Da
Sätze und Konstruktionen auch in der Euklidischen Geometrie,
angeführten
Ausnahme
0,
das Paar
der Ebene darstellt.
die
=
25, da
von
den 3
Brennpunktepaaren
ein
nur
einziges
mit
reelles Paar
bleibt.
Satz 29:
Die
Der konstante Winkel
5.
§
Strecke, die
von
zwei festen
Tangente abgeschnitten
veränderlichen
Brennpunkt.
am
Tangenten
wird, erscheint
von
Kegelschnittes auf einer
jedem Brennpunkt unter einem
eines
konstanten Winkel.1
der Konstanz des
Doppelverhältnisses der
Tangente
gegebenen Tangenten und
den
durch
Brennpunkt geschnitten wird (Fig. 11).
isotropen Tangenten
Der Beweis
ergibt
sich einfach
aus
durch die beiden
in denen die veränderliche
Sind die
Brennpunkte uneigentlich,
Satz 30:
Die
Fällt die variable
so
folgt
Normalprojektion der Strecke,
Tangente abgeschnitten wird, auf
veränderlichen
genten,
so
Tangente
nacheinander
die
von
eine
zwei festen
Brenngerade,
zusammen
mit
jeder
Satz 31 : Der Brennstrahl nach dem
Satz 32:
Die
Brenngerade
Kegelschnitt.
wird
halbiert
durch
von
Der Pol einer
Sehne, das
Story:
auf einer
Länge.
der beiden festen Tan¬
Schnittpunkt zweier Tangenten
Berührungspunkten. Oder
Normalprojektion
Als besonderer Fall
Satz 33:
1
Tangenten
hat konstante
erhalten wir den
der Brennstrahlen nach den
zur
Punkte,
4
die beiden
man
a.a.O.
im
S. 12.
einer
die
beliebigen
Projektion des
halbiert den Winkel
Sehne eines
Poles
der
Kegelschnittes
Sehne in Bezug
auf eine
auf den
Satz 31 erscheint der
beliebigen
Sehne durch einen
Brennpunkt errichten
kann.
Brennpunkt liegt
auf dem Lot
29
Weiter
gilt
Satz 34:
der
Die
beliebigen Tangente von zwei gegenüberliegenden Scheitel¬
von jedem Brennpunkt der die beiden Scheitelpunkte
unter einem rechten Winkel gesehen.
auf einer
tangenten abgeschnittene Strecke wird
verbindenden Achse
Es
ergeben
Satz 35:
aus
sich noch die
Dreht sich
folgenden
Ortssätze:
ein konstanter Winkel
seinen
um
Scheitelpunkt,
so
umhüllt die
Verbindungslinie der Schnittpunkte der beiden Schenkel mit zwei festen Geraden ein Paar
von
Kegelschnitten, von denen jeder die beiden festen Geraden berührt und den festen
Scheitelpunkt des sich drehenden Winkels zum Brennpunkt hat.
Wir erhalten noch die Berührungspunkte der beiden festen Tangenten mit den beiden
Kegelschnitten, wenn wir vom Brennstrahl ihres Schnittpunktes aus den gegebenen Winkel
nach beiden Seiten abtragen.
Die beiden Kegelschnitte des Satzes 35 fallen in einen zusammen, wenn der sich
drehende Winkel
gleich
—
ist.
Der
Schnittpunkt
der
Schnittpunkten der Schenkel des rechten Winkels mit
eine gerade Linie, wenn der rechte Winkel sich um
Brennpunkt des Kegelschnittes zugeordnete Leitlinie.
Verbindungslinien
der Paare
von
den beiden festen Geraden beschreibt
seinen
Scheitelpunkt
dreht:
die dem
30
Satz 36: Dreht sich ein rechter Winkel
dessen Schenkel zwei
beliebige
Lote
zu
Schnittpunkte einen Kegelschnitt,
gegebene Gerade Symmetrieachse ist,
tangenten bilden.
der
Ein weiterer
Spezialfall
Satz 37: Zieht
man
von
einen Punkt einer Geraden und schneiden
um
dieser
Geraden,
während
die
umhüllt die Verbindungslinie
Scheitelpunkt Brennpunkt, die
so
für welche der feste
beiden
Lote ein
Paar
Ton
Scheitel¬
Satz 31 ist
durch einen
Brennpunkt
die beiden Parallelen
zu
einer
Asymptote,
Winkel halbiert durch den Brennstrahl nach dem der
gebildete
Asymptote entsprechenden Leitpunkt (siehe Fig. 12).
Satz 38: Fällt man auf eine Brenngerade Lote, die zu einer Asymptote nach verschiedenen
Seiten parallel sind, so wird die Projektion der Asymptote auf die Brenngerade halbiert
durch die Projektion des zur Asymptote gehörigen Leitpunktes.
Aufgabe 6: Ein Kegelschnitt sei gegeben durch einen Brennpunkt und drei beliebige
Tangenten. Man konstruiere die Berührungspunkte der Tangenten.
Lösung: a, b, t seien die 3 gegebenen Tangenten (siehe Fig. 11), C, D, P die Schnitt¬
punkte von {a, t), (b, t), (a, b). Verbinden wir diese 3 Punkte mit dem gegebenen Brenn¬
punkt F und tragen wir den <J CFD in F an FF nach beiden Seiten an, so schneiden
die zweiten Schenkel F A und FB die Tangenten a und b in den gesuchten Berührungs¬
punkten A und B.
so
wird der
von
diesen
'
31
Aufgabe 7: Den Leitpunkt zu einer gegebenen, zu einer der eigentlichen Achsen senk¬
rechten Asymptote eines Kegelschnittes zu konstruieren, wenn ein Brennpunkt der andern
eigentlichen Achse gegeben ist.
Lösung : Wir ziehen (siehe Fig. 12) durch den gegebenen Brennpunkt die beidseitigen
Parallelen zur Asymptote, halbieren den von diesen gebildeten Winkel.
Die Winkel¬
halbierenden schneiden die zur Asymptote senkrechte Achse in zwei Punkten L und R*i
von denen ersterer Leitpunkt eines Kegelschnittes, letzterer dagegen der
Asymptotenpunkt
desselben ist. Die Lösung ist also eindeutig.
Es seien W, W die beiden Endpunkte der Asymptote h, FW und F W die beiden
Parallelen durch den gegebenen Brennpunkt, V, bezw. V deren zweite absolute Punkte.
Die eine Winkelhalbierende n geht durch den Pol M* der andern, der sich ergibt als
h und VV.
Die andere, m, muß, da sie die Polare
Schnittpunkt der Geraden WW
eines Punktes der Asymptote h ist, auf h senkrecht stehen.
Gestützt auf diese Tatsache
läßt sich die Konstruktion des Leitpunktes wesentlich vereinfachen : Wir fallen vom Brenn¬
punkt F das Lot auf die gegebene Asymptote h, errichten im Brennpunkt zu diesem Lot
eine Normale.
Diese trifft die zu h senkrechte Achse im gesuchten Leitpunkt.
Von den Sätzen dieses Paragraphen kommen beim Übergang zu Euklidischer Ma߬
bestimmung nur 30 und 32, die sich auf die einem Brennpunkte zugeordnete Brenngerade,
also dessen absolute Polare, beziehen, in Wegfall, indem diese Geraden mit der unendlich
=
fernen Geraden koinzidieren.
§
6.
Beziehungen zwischen Asymptoten
und
Brennpunkten.
Bezeichnen wir mit <p8 den Winkel der Asymptoten hs, h3' gegen die Achse x1
0,
d, und dt die Abstände der Asymptoten \, ht', bezw, hv h2' vom eigentlichen Mittel¬
punkt Oâ, mit alt a2 die Abstände der auf olt resp. o2 liegenden Scheitelpunkte von Os,
mit (pg den Winkel der durch Os hindurch gehenden Scheiteltangenten, mit ct,
c2 die Ent¬
fernungen der Brennpunkte auf ot und o2, mit Xs ^e Winkel, den die Richtungen nach
den beiden Brennpunkten auf o3 mit der Achse ot bilden, so ergeben sich aus den Grund¬
formeln des § 1 die Formeln
=
mit
/-!
1/ CTli+^2a38
\
(i b)
ch
(K)=i/
'
do
(2b)
*
y -%»
M22
h
1/
•
,
sh
ai"
a22
K
USS
*
(kaj
=
1/
'
°"
°11
~T
K
a33
,
l/—
'
m={/ £-fc. («.)=F^^.
ch
.
O.
—
fC
C&-\-\
(m^v a"+F"»8, th (*a1)=i/j^±^&-.
'
W3S
ft2ß33
A
<*«,)=
1/~f""
'
ail "t"
K
ß33
,
ail
U2i
koo
k
«
w-Y=\
th
(lo,)= !/
'
k
ass
Oi±
32
(2 c)
^
cos
j*(4ei)
(3a)
=
|/__fiî—,
*
=
<*
(fc c2)
v
2
'
=
«U
(—
"
«22
ft
N
,„
cos
«22
(&c i;)
«33)
*
=
1/
—
(* C2)
=
A
Ä2
(—
an
(jfc }
v
_
1/
Hieraus ergeben
herausgreifen :
(4)
sich eine
sh (k
(5)
sh
Menge
d±)
(Je d2)
von
=
ctg
==
tg
ft
,_,.
(7)
—
«22
—
«
V
«33J
a22(an-f-£ «33)'
«22)
fc2 a33)
-
—
«22
"
=
-
(«11 H~ ^ «33)
(an
a22)
fc a33
«22 Ki + *' «33)
«„(-Om-ä'o,,)-
Beziehungen,
cp3, ft
ips, ft
(Ä (Üj)
-ftVt"=
Die
(
*
—
-
Qc «"J
(7c rt"2)
*Ä(A<y •*&(*<*,)
(6)
«11
f
(«11
Xs
«11
1/ —A2«33(«ii— «22)
=
.
x»=r-^W-'d'sm
tgX8_r
'
1/
a„)
l/-3*-
^
"
a22
=
r*> (a" -;?22)
(a„ + /c2 a33)
|/~f ^33
r
—
s
«33)
*
«22
A(tO=
a22
tg 4>3
,
^
r
(«u +
f_
-«i»
«11
'
—
l/«ii (— «2»
1/
=
]/a»(-q^ + fe2«33)
—
(3c)
^
K=^^5H
ft
(3b)
sin
«22
#11
tg
=
=
=
von
welchen wir
cos
cp3.
nur
einige wenige
sin cp3.
1.
*"
(5) stellen nichts anderes dar, als die Beziehung zwischen dem
zugehörigen Lot. Mit Hilfe der Beziehung (6) läßt sich der Ab¬
stand der zu einer Achse senkrechten Asymptoten aus demjenigen der zur andern Achse
senkrechten Asymptoten durch Rechnung ableiten. Wichtiger sind für uns die Beziehungen
(8) und (9), weil diese sich konstruktiv verwerten lassen.
Es sei S ein Scheitel der Achse o2.
Die Scheiteltangente s im Punkte S treffe die
Beziehungen (4)
und
Parallelwinkel und dem
Asymptote h3
liefert
uns
im
Punkte A.
<J SOaA
TZ
=
-=
Die
cp3.
hyperbolische Trigonometrie
nun:
ft
Satz 39
Die
(h
v
•
OtA)
3
'
=
**(*"»)
sin
<p3
=
th
Qe c2),
v
2y'
d. h.
Schnittpunkte der beiden Asymptoten durch den eigentlichen Mittelpunkt
mit den Tangenten in den Scheitelpunkten einer eigentlichen Achse liegen mit den Brenn¬
punkten dieser Achse auf einem Kreis um den eigentlichen Mittelpunkt (siehe Fig. 13).
:
33
Brennpunkte, wenn die Asymptoten durch
den eigentlichen Mittelpunkt und die auf einer eigentlichen Achse liegenden Scheitelpunkte
gegeben sind. Umgekehrt lassen sich auch Scheitelpunkte und Asymptoten aus den be¬
ziehungsweisen andern beiden Elementen konstruieren.
Daraus fließt eine einfache Konstruktion der
o2
Maßbestimmung
Bei Euklidischer
in der Ebene
gehen
die Formeln
(8)
und
(9)
über in
die bekannte Relation:
a
sin
cp
=
.
Ebenso läßt sich
rechten
Asymptoten
Scheitelpunkten mit
zeigen,
den
gilt
punkte
»Achse"
der
zu
eigentlichen Achse senk¬
eigentlichen Achse liegenden
auf einer Abstandslinie liegen,
einer
in den auf der andern
der letzteren Achse
hat.
der
Satz 40: Verbindet
zweiten Achse,
zur
c
Schnittpunkte
Tangenten
Brennpunkten
mit den
welche die erste Achse
Dual
daß die
•—.
so
lotrechten
Scheitelpunkte einer Achse mit den Brennpunkten einer
Verbindungslinien, sowie die auf der Achse der Scheitel¬
Asymptoten einen Kreis, der die Verbindung der beiden Brennpunkte
man
die
umhüllen diese 4
5
34
zur
Achse hat.
„Abstandslinie"
Wir leiten
Asymptoten
und
Ziehen wir
liebigen
(Hiebei ist unter „Kreis" sowohl der
zu verstehen.)
im folgenden auf synthetischem Wege
Brennpunkten
(siehe Fig. 14)
Brennstrahl s,
so
Kreis im engeren
noch eine weitere
Sinn,
als auch die
Beziehung
zwischen
ab:
durch einen
Brennpunkt
mögen die Schnittpunkte
von
F eines
s
Kegelschnittes
mit dem A. K.
w
einen be¬
und dem ge-
gebenenen Kegelschnitt 1c mit U, V, bezw. mit S, T bezeichnet werden. Wir können die
Kegelschnitte auseinander hervorgehen lassen durch eine kollineare Transformation,
in welcher F KoUineationszentrum, eine der beiden Asymptoten, welche auf der Achse des
Brennpunktes F senkrecht stehen, aber Kollineationsachse ist. Hieraus folgt, daß die
Tangenten in den Punkten S, T, U, V sich paarweise in zwei Punkten der Asymptote
treffen. Dies gilt sowohl für die eine, wie auch für die andere der beiden Asymptoten h, h'.
Es treffen sich also die Tangenten in S, ü in einem Punkte Q, diejenigen in T, V in
einem Punkte P von h, die Tangenten in S, V in einem Punkte B', diejenigen in T, U
in einem Punkte P1 der zugeordneten Asymptote h'.
Ziehen wir durch den F zugeordneten Brennpunkt F' gleichfalls den Brennstrahl s'
beiden
35
durch den einen
die beiden Paare
mit dem
Schnittpunkt T von s
von Schnittpunkten
von
Kegelschnitt
1c und sind
s' mit k und dem A. K. to,
S', T, bezw. U', V
treffen sich die
so
von h',
S',
diejenigen
Tangenten
einem
Punkte
in
in
U'
die Tangenten in S', V dagegen in einem Punkte B, diejenigen
T,
von h, der mit demjenigen der Tangenten in T, V von vorhin identisch ist.
Die Verbindungslinien U' V, bezw. UV sind die absoluten Polaren der Punkte P, P'
auf h, bezw. h', stehen somit senkrecht auf h, resp. h', laufen infolgedessen durch die h
und h' entsprechenden Asymptotenpunkte 3*, bezw. H'*, stehen beide endlich senkrecht
auf der Tangente t des Punktes T. Die Verbindungslinien ÜU', bezw. VV stehen senk¬
recht auf der Normalen n des Punktes T, mit andern Worten der Tangente des zweiten
durch T hindurch gehenden Kegelschnittes.
U' in einem Punkte Q',
in
Satz 41 : Ziehen wir
von
den beiden
in T, V in einem Punkte P
Brennpunkten
eines Paares die Brennstrahlen nach
gemeinsamen Parallelen dieser
Kegelschnittes,
auf
Punktes
und
des
denjenigen beiden Asymptoten senk¬
Tangente
recht, die auf der Achse der Brennpunkte normal stehen. Sie gehen somit durch die den
Asymptoten homologen Asymptotenpunkte. Das andere Paar von gemeinsamen Parallelen
steht zu demjenigen Kegelschnitt, der durch 1 geht und zum ersten konfokal ist, in der¬
selben Beziehung in Bezug auf die Normale des gegebenen Punktes.
einem Punkt eines
so
stehen zwei der vier
Brennstrahlen auf der
Umgekehrt gilt
der
gemeinschaftlichen Lote einer gegebenen Kegelschnitts¬
gegebenen zusammengehörigen Asymptoten und ermittelt man
tangente
die gemeinsamen Parallelen dieser Lote, so gehen diese Parallelen durch die zwei Paare
auf der zu den Asymptoten senkrechten Achse, die denjenigen beiden
von Brennpunkten
Kegelschnitten angehören, welche die gegebene Tangente berühren, sowie durch die Be¬
rührungspunkte der Tangente mit diesen Kegelschnitten.
Aufgäbe 8: Von einem Kegelschnitt seien gegeben zwei zusammengehörige Brenn¬
punkte F, F', sowie ein beliebiger Punkt 1. Es sollen die zur Achse der Brennpunkte
senkrechten Asymptoten bestimmt werden.
Lösung: Wir zeichnen (siehe Fig. 14) die Brennstrahlen Fl und F'T. Diese mögen
Ermitteln wir die gemeinsamen Parallelen
den A. K. in U, V, bezw. U', V schneiden.
Satz 42:
Bestimmt
man
die
mit zwei ebenfalls
'
U'V,
bezw.
UV,
so
treffen
dieselben
die Achse FF'
=
o2 in
zwei Punkten S*,
H'*,
Asymptotenpunkten
gehenden Kegelschnitte. Die ge¬
meinschaftlichen Lote von ü' V und o2 einerseits und von UV und o2 anderseits sind die
gesuchten Asymptoten h und h'. Die Aufgabe läßt zwei Lösungen zu.
den
des
einen
der beiden durch 1
Aufgabe 9: Ein Kegelschnitt sei bestimmt durch ein Paar von Asymptoten h, h' und
beliebige Tangente t. Man konstruiere die Brennpunkte der zu h, h' normalen Achse.
Lösung : Die gesuchten Brennpunkte werden nur dann reell, wenn die gegebene Tangente
Wir setzen dies also voraus und kon¬
die Asymptoten nicht im Eigentlichen schneidet.
struieren dann (siehe Fig. 14) die gemeinschaftlichen Lote von t und h einerseits und von
t und h' anderseits und schneiden dieselben mit dem A. K. in den Punkten U\ V, resp.
U, V. Bestimmen wir nun die gemeinsamen Parallelen UV, bezw. U'V, so begegnen
diese der zu h, h' senkrechten Achse in zwei Punkten F, F', den gesuchten Brennpunkten
eine
36
eines der beiden
Kegelschnitte,
die die Gerade t
Brennpunkten
erhalten wir auf bekannte Weise
ebenfalls zwei
Lösungen.
zur
die
Tangente
haben.
Brenngeraden.'
uneigentlichen
Aufgabe besitzt
Bei
Die
Aufgabe 10: Es sollen die Schnittpunkte eines Kegelschnittes mit einer Geraden durch
einen Brennpunkt desselben konstruiert werden, wenn der zugeordnete Brennpunkt uud
das
diesem
Brennpunktepaar homologe Asymptotenpaar gegeben sind.
U, V die absoluten Punkte der gegebenen Geraden durch den gegebenen
Lösung
F
Brennpunkt
(siehe Fig. 14), so ziehen wir zwei ungleichsinnige Parallelen VU', UV
senkrecht zu je einer der beiden gegebenen Asymptoten h, h', wo U', V die zweiten Enden
dieser Parallelen sind.
Die Verbindung U'V trifft die gegebene Gerade in einem der
beiden Schnittpunkte mit dem Kegelschnitt. Die Tangente in diesem Punkt ist die Winkel¬
halbierende des Winkels der gegebenen Geraden UV und der letzten gemeinsamen Parallelen
U'V und zwar diejenige, die zu VU' und UV gleichzeitig senkrecht steht. Die'Gerade
U'V geht durch den F zugeordneten Brennpunkt F'.
Vertauschen wir bei den beiden
Normalen zu h, bezw. h' die Kichtung des Parallelismus in Bezug auf die Gerade UV, so
erhalten wir in gleicher Weise den zweiten Schnittpunkt der gegebenen Geraden mit dem
Kegelschnitt. Die Konstruktion ist auch ausführbar bei uneigentlichen Asymptoten.
Aufgabe 11: Von einem Kegelschnitt seien gegeben ein Paar von Brennpunkten und
hiezu
die
homologen Asymptoten. Es sollen die Tangenten von einem Punkt einer dieser
Asymptoten an den Kegelschnitt konstruiert werden.
Lösung: Nachstehende direkte Konstruktion der Tangenten ist nur dann reell durch¬
führbar, wenn der gegebene Punkt der Asymptote als uneigentlicher Punkt angenommen
Es sind also dann im eigentlichen Gebiet die Tangenten des Kegelschnittes senk¬
wird.
recht zu einer Normalen zu einer Asymptote oder einer Geraden durch einen Asymptoten¬
zu
:
punkt
zu
Sind
konstruieren.
U' V, wo
gegebenen Punkt P als uneigentlich voraus, ist p*
sind, seine absolute Polare, so haben wir U' und V nur mit den
beiden gegebenen Brennpunkten F, F' zu verbinden. Die Schnittpunkte dieser beiden Paare
der gesuchten Tangenten.
von Verbindungslinien sind die Berührungspunkte
(In Fig. 14
ist nur eingezeichnet, was zur Konstruktion der einen von beiden Tangenten nötig ist, wie
Setzen wir somit den
U',
=
V absolute Punkte
sie auch
zur vorangehenden Aufgabe
Schnittpunkte zeigt.)
§
Wir stellen
uns
7.
nur
die Konstruktion des einen der beiden
Konjugierte
gesuchten
Durchmesser.
die
gegebenen Punkt P {yv y2, y3) eine Gerade zu ziehen, auf
gegebener Kegelschnitt eine Sehne herausschneidet, die P zum Mittelpunkt hat.
Lösung: Die gesuchte Gerade wird vom A. K. o) und dem gegebenen Kegelschnitt &
in Punktepaaren einer Involution geschnitten, deren einer Doppelpunkt der gegebene
Der andere Doppelpunkt ist der Schnittpunkt Q der Polaren p* und p des
Punkt P ist.
Punktes P in Bezug auf w und Je (siehe Fig. 15).
Aufgabe
welcher ein
12: Durch einen
37
Es seien
(1)
w„
(2)
Jcxx
die
in
Gleichungen
Bezug auf co
und Je sind dann
t»xy
(4)
kxy
=
bemerken, daß
das Verhältnis yx
:
0
*,a!11 + fc,V-V
allx1i-{-aaixis + a8,x82
=
a
.
a
•
a
•
0
gegebenen Kegelschnittes.
gegeben durch die Gleichungen:
+ 7c2
#*,
yt x2
-\- a22
an yx xx
von
=
Die Polaren
Je2 yx xx
=
Schnittpunkt Q
(5)
Wir
=
des A. K. und des
(3)
Für den
=
^)
xx
=
#2
=
xs
=
—
y2 x2
ergeben
ysxs
-\-
von
P
=
0
sich die Koordinaten:
•
—
*
—
und p
0
=
aa3 ys xz
J2 ag8)
&2
a3S)
-f
(an
2/i
ä2 (au
a22) «^
(— a22
p*
•
y2 y3 K
2/3
»
y2.
das Verhältnis xt
Bezeichnen
wir
: x2 konstant ist, wenn dasselbe der Fall ist für
letzteres mit fi3, ersteres mit \l3', so können wir
y2.
sagen: Wenn der Punkt P sich auf einem Durchmesser xx
ji3 x2 = 0
der Schnittpunkt der beiden Polaren einen zweiten Durchmesser x1
ergibt sich
—
—
bewegt,
|V x2
so
=
0.
beschreibt
Aus
(5)
38
(— a22
(«u +
¥
—
/
_
W
g83)
a88)
•
y2
•
—
_
î/1
aM
¥aS3
—
+¥
an
^
J_
a33
|i8
oder
(6)
h
Wir
bezeichnen
ein
h'
'
Paar
-^f^3
=
"il ~r
K
Durchmesser
solcher
konst.
=
a88
als
»konjugierte
Durchmesser"
des
Kegelschnittes.1
Winkel, welche zwei konjugierte Durchmesser mit der Achse ot
tg a, (x3'
tg a'; |i3, [i.jJ sind also die »Richtungskoeffizienten" der
Bedeuten a, a' die
bilden,
so
ist [i3
=
=
beiden Durchmesser.
Setzen wir u.s
|x8',
=
«22
so
"'"
finden wir
°88
2
~R*>'
«ii+*2«as
so
daß wir nach
§
6 Formel
(la)
den Satz
aussprechen
können:
Richtungskoeffizienten konjugierter Durchmesser ist konstant,
gleich dem Quadrat der Richtungskoeffizienten der beiden durch den eigentlichen
Mittelpunkt gehenden Asymptoten.
Die Gleichung (6) kann, wenn wir statt der [i die Verhältnisse y1 : y2 und x1 : x2 wieder
einführen, in der Form geschrieben werden:
Satz 43: Das Produkt der
nämlich
(7)
(an -f
.
¥
ass) y1
x±
+ (a22
a83) y2
-f- ¥
Dies ist aber nichts anderes als die Polarform der
(8)
(ou
^
welche das durch o3
+¥
a38) x±* + (a22 +
gehende Asymptotenpaar
¥
x2
=
0.
Gleichung:
ass) x22
darstellt.
0,
=
Daraus
folgt
der
liegen harmonisch in Bezug auf dasjenige Paar von
Mittelpunkt hindurchgehen. Die beiden eigentlichen
Asymptoten,
Achsen sind dasjenige Paar konjugierter Durchmesser, die aufeinander senkrecht stehen, die
Asymptoten sind diejenigen Durchmesser, die mit ihren konjugierten zusammenfallen.
Ersetzen wir den Kegelschnitt Ti durch einen beliebigen zu Ti homothetischen Kegel¬
Satz 44 :
Konjugierte
die
durch
Durchmesser
denselben
schnitt
(9)
so
Jcxx
Xwxx
—
=
(a„
—
finden wir für die Polare
hxy
(10)
—
X tüxy
=
(an
p*
—
Für die Koordinaten des
(«11 +
Gleichung (7).
d. h.
Es
'¥ X) yx xx + (a22
ergibt
«as)
Vi xi
1
in
auf alle
Vgl. Killing:
a.a.O.
Kegelschnitte
S. 12.
Bezug
¥
X)
auf
(9)
finden wir die
+ («22 +
&2
daß
konjugiert
«83) Vi
in
Bezug
des homothetischen
konjugierte
die
=
x2
°>
Gleichung:
+ («3s + *) Vi
y2 x2
xs
=
0-
Beziehung:
=
sich also genau derselbe Punkt
Bezug
(Dies folgt übrigens auch daraus,
auf das Paar der Asymptoten.)
es
—
Schnittpunktes Q
&
*) V + («83 + *) xs2
&2
—
des Punktes P in
Satz 45: Sind zwei Durchmesser
sie
+ («22
¥ X) x2
0,
Q.
auf einen
Kegelschnitt, so sind
angehört.
harmonisch sind in Bezug
Büschels,
Durchmesser
dem ersterer
39
1st
X1
die
Gleichung
eines
jl3 #2
beliebigen Durchmessers,
gebracht werden:
=
U
kann
so
die
Gleichung
des
konjugierten
Durchmessers in die Form
Kl +
1*3
&2
ß8a)
X\
+ («22 +
«3s) «2
=
°
natürlich auch für solche Durchmesser, die durch einen
Das
Gesagte gilt
Mittelpunkt gehen, also auf einer der eigentlichen
einzig die Bedeutung der u.. Setzen wir
Vi
'
H-3 =.Vi
'
1*1
so
fc2
—
y3
f*i
»
Achse senkrecht stehen.
—
x2
V*'=*i
2/a.
•
%3
'
•
^3
'
uneigentlichen
Es ändert sich
ist
1*1
'
~T~
Hi'
(U)
fA2
Bezeichnen wir mit
normalen
*
«22)
*
7.2 /~
«33
..
konst.
=
"v
bezw.
(Je d±)
(Je d2)
th
es
a83
d2, d2 die Abstände zweier
konjugierten Durchmesser vom eigentlichen Mittelpunkt,
th
und
*
1
«22
hi'
dv d^,
tt22
(«jj
«
—
=
Je [t,t, th
Je u-2, th
(Je «"/)
(Je d2)
=
Je
=
Je
Achse ov bezw. o2'
ist
zur
so
n/,
(i2',
ist dann:
(Je dt)
th
•
(Je djO
th
Ä2
=
•
|ij
|V
(12)
_
(Je d2)
th
•
th
(Je d2')
W-\l2 n,'
=
a"+^8g33
°^_ „°"
""
CTa3
=
=
=
konst.
=
konst.
_
Wir wollen
die
mit Je
koeffizienten" bezeichnen.
Satz 46:
multiplizierten Koeffizienten
gilt dann der
fi/;
\i±,
(i2)
[i2'
als
„Abstands¬
Es
Das Produkt
der Abstandskoeffizienten
Durchmesser ist konstant, nämlich
zweier
konjugierter
achsennormaler
Quadrat des Abstandskoeffizienten der
gleich
Asymptoten.
Brennpunkt gehörigen
dem
zur
betreffenden Achse normalen
Satz 47: Die
konjugierter
zu
einem
Beweis: Die Koordinaten eines der beiden
(13)
Die
(14)
QFj-)
Geichung
an
Ihr
Leit- und
Brenngeraden
bilden ein Paar
Durchmesser.
der
V
—
a
•
a
•
a
•
xl=
V
x2
=
V an (a22 -f- Je2 am)
x3
=
0
zugehörigen
«22
(«n ~~\~
Richtungskoeffizient
Brennpunkte
k2
—
«22
(an "H
&2
z.B. auf os sind:
a3s)
Leitlinie lautet:
ass)
•
-\- a22 V
xx
an
(a22 -f- Je2 as3)
ist
_
«22
AI
«11
'
(«22 ~r
«33)
«22 («11 4" &* «3.0
«11
*
'
•
x2
=
0
40
Die
Gleichung
V
(16)
mit dem
der
—
zugehörigen Brenngeraden
aM
(an
+ Je2
a33)
•
V an (a22 + k2 a33)
x2
•
=
0
Richtungskoeffizienten:
.t'
(17)
=
—l/^fr*" +,^3ä\.
'
—
«22
daß
so
x% +
ist:
-
•-•-
Kl + * «33)
F ~ai+i-1,?
-•"-•
Ist P ein Punkt des
dem
Schnittpunkt
der
Kegelschnittes Je, so wird die Verbindungslinie des Punktes P mit
Polaren, dem konjugierten Punkt zu P in Bezug auf das durch A
bestimmte homothetische Büschel,
zur
der KurTennormalen im Punkte P.
alle
Kegelschnitte
Tangente
und
Q
Die Polaren des
ist dann einfach der absolute Pol
gegebenen
Punktes P in
Bezug
auf
des Büschels stehen dann auf dieser Normalen senkrecht.
Satz 48: Die Polaren eines
gegebenen Punktes in Bezug auf alle Kegelschnitte eines
homothetichen Büschels stehen senkrecht auf dem Lot
zur Tangente im gegebenen Punkt
geht.
Satz 49: Die Polare eines Punktes einer Asymptote in Bezug auf den Kegelschnitt
steht senkrecht auf dem Lot zur Asymptote im gegebenen Punkt.
Da die Asymptoten die Doppelstrahlen der Inyolution der Paare konjugierter Durch¬
messer darstellen, so müssen diese Asymptoten reell oder imaginär ausfallen, je nachdem
diese Involution hyperbolisch oder elliptisch ist, d. h.
Satz 50: Die Asymptoten eines Kegelschnittes sind reell oder imaginär, je nachdem
die Paare konjugierter Durchmesser des Kegelschnittes durch die Achsen nicht getrennt
oder aber getrennt werden, oder mit andern Worten je nachdem die beiden Durchmesser
eines jeden Paares durch den gleichen oder durch verschiedene Quadranten der Ebene
gehen.1 Konjugierte Durchmesser einer Ellipse gehen also stets durch verschiedene Quadranten,
konjugierte Durchmesser einer jeden eigentlichen, konkaven oder konvexen Hyperbel gehen
an
denjenigen Kegelschnitt,
der durch diesen Punkt
.
immer durch denselben Quadranten.
Wenn wir
so
muß
die
schließlich
nun
gesuchte
die
zu
Anfang
des
§ gestellte Aufgabe erledigen wollen,
Gerade senkrecht stehen auf der absoluten Polaren des
zu
P kon¬
jugierten Punktes Q in Bezug auf das Büschel homothetischer Kegelschnitte. Der durch Q
gehende Durchmesser muß ebenfalls senkrecht stehen auf der genannten Polaren q*. Es
gilt, da q* Kurvennormale ist, wenn P auf dem Kegelschnitt liegt, der
Satz 51: Der konjugierte Durchmesser zu demjenigen durch einen gegebenen Punkt
steht senkrecht zum Lot zur Tangente im gegebenen Punkt an denjenigen Kegelschnitt,
der durch den Punkt hindurchgeht.
Satz 52: Die Kurvennormalen in den Schnittpunkten eines gegebenen Durchmessers
mit sämtlichen Kegelschnitten eines homothetischen Büschels haben den konjugierten Durch¬
messer zum gemeinschaftlichen Lot.
1
M. Zacharias
:
Realitätskriterien für
euklidischen Geometrie.
Sitzungsberichte
Brennpunkte
und
Asymptoten
der Berliner Math. Gesellschaft.
der
Kegelschnitte
1922.
in
der nicht-
41
Der Satz 51 liefert
eine
Tangente in einem
Asymptotenpaar bekannt ist. Umgekehrt
läßt sich auch der konjugierte Durchmesser zu einem gegebenen leicht konstruieren, wenn
die Tangente des Schnittpunktes mit dem Kegelschnitt gegeben ist
Gehen wir zu Euklidischer Maßbestimniung über, so geht unsere Durchmesserinvolution
über in diejenige der konjugierten Durchmesser in der Euklidischen Geometrie. Der einem
gegebenen Punkte P zugeordnete Punkt Q fällt auf die unendlich ferne Gerade. Satz 48
geht über in den Satz: Die Polaren eines Punktes in Bezug auf ein Büschel ähnlicher und
ähnlich gelegener Kegelschnitte sind parallel; sie stehen senkrecht auf dem Lot zur Tangente
im gegebenen Punkt an denjenigen Kegelschnitt des Büschels, der durch den gegebenen
Punkt geht.
Die Sätze 43 und 44 gelten unverändert auch in der Euklidischen Ebene,
gegebenen
wobei
gilt
Punkt eines
zwar
uns
sehr einfache Konstruktion der
neue,
Kegelschnittes,
das konstante Produkt der
wenn
ein
Richtungskoeffizienten gleich
—
wird.
Satz 45
bei
gleichem Wortlaut für das Büschel ähnlicher und ähnlich gelegener Kegelschnitte.
geht über in : Der konjugierte Durchmesser ist parallel zu den Tangenten in den
Schnittpunkten des gegebenen Durchmessers mit dem Kegelschnitt. Satz 52 lautet in der
Euklidischen Geometrie : Die Tangenten in den Schnittpunkten eines Durchmessers mit den
Kegelschnitten eines Büschels ähnlicher und ähnlich gelegener Kegelschnitte sind unter sich
parallel. Satz 50 endlich über die Realität der Asymptoten überträgt sich ohne jede
Satz 51
Änderung
auf die Euklidische Geometrie.
§ 8.
Wir stellen
Aufgabe
schaft,
uns
die
13: Auf einer
daß die
Konjugierte Achsenpunkte.
Tangenten
beliebigen Geraden^ einen Punkt S
S an einen gegebenen Kegelschnitt
von
zu
finden
von
der
mit der Geraden p
Eigen¬
gleiche
Winkel bilden.
Lösimg:
gesuchte
Der
Punkt ist der
Schnittpunkt der Geraden p mit der Verbindungs¬
gegebenen Kegelschnitt Je mit dem absoluten
Pol P* der Geraden p.
Die Gerade q ist zu p konjugiert in Bezug auf die durch Je und w
bestimmte konfokale Schar (siehe Fig. 16).1
linie q des Poles P
von
p in
Bezug
auf den
Ist
(1)
die
QK
Gleichung
des
Kegelschnittes
(2)
%
diejenige des Kegelschnittes Je
gegebenen Geraden p, so
der
auf
(o
=
=
^ + ^-^32
=
œ,
Än ^ + Ä2, & + ^33 &
in Linienkoordinaten und sind
lauten die
Gleichungen
=
(ija,
0
rj2,
%) die Linienkoordinaten
der Pole P!: und P
von
p in
Bezug
und Je:
(3)
2ft
=
1iÇi+ %&-*•% §s
(4)
Z'grj
=
Al
1
0
Killing:
a. a.
Vi
?i 4- Aiî
Vi
=
0
Es + ^33
%
§3
=
°
0. S. 12.
6
42
Für die
Verbindungsgerade F*P=q
(5)
a
•
a
•
a
•
^
g,
f,
=
=
=
erhalten wir die Koordinaten:
(Je2 A22 + Ä33) ij, %,
(— Ä2 4U
4,,) iji rj3,
—
(^22
—
^u)
y)! ij,.
Die Gerade # schneidet ^? unter einem rechten Winkel, da ja q durch den absoluten
Pol P* von p geht. Sie läßt sich daher einfach konstruieren als Lot zu p vom Pol P der
Geraden p
bezüglich
Die Pole
von
p in
Satz 53:
Schar
k.
Bezug auf alle Kegelschnitte der
Kegelschnitt die gegebene Gerade p,
Bezug auf den betreffenden Kegelschnitt.
von
Die
p in
Pole
einer Geraden
auf der Normalen"
liegen
einem Kegelschnitt
Speziell folgt:
konfokalen Schar
zu
zur
in
Bezug
gegebenen
so
Also
auf alle
ist der
gilt
liegen sämtlich
Berührungspunkt der
der
Kegelschnitte
Geraden im Punkte,
wo
einer konfokalen
die Gerade
von
der Schar berührt wird.
Salz 54: Die Pole
punkt
Kegelschnittes
Berührt ein
auf q.
Pol
des
einer Geraden durch einen
dieser Geraden errichteten Lot.
Brennpunkt liegen
auf dem im Brenn¬
43
Bezeichnen wir die Verhältnisse rj3
Xx, X2, X3,
X/, X3', X3',
bezw.
7]3, f]3
:
ergeben
so
sich
x2. v
As
Über
der
die
A
die
:
Çlt Ç2
:
^
mit
-^33
konst-
=
"^-22 T^ -^33
—
j.2
Konst.
—
\
a
11
Schnittpunktes
a
Entfernung
Desgleichen
Ç2, £3
Beziehungen:
:
a
^22 T -^-33
folgendes
sagen:
Die
Gleichung
Geraden p lautet:
Die Koordinaten des
<*(tel)
(5)
A "T^1
-
Vi xi
Seine
:
der Koeffizienten X können wir
Bedeutung
gegebenen
A3
*
=
Ç3
ï}t, bezw.
njlt Y)3
aus
-^-11
*
(6)
:
=
#!
ist
0S
von
•
=
V
7)22
fc2
03,
a
finden wir für die
#2
•
Vb X3
=
°
=
finden wir:
a
%,
•
x3
—
tj2.
—
durch:
*<**>
rj32
+
X2
p mit ot
von
gegeben
77=T==f
-
+ Vi
AT-i^T-r
=
V T)32
Entfernung
des
—
*"
tt(Äe^
rj38
=
-^-
=
*V
Tj3
Schnittpunktes
konjugierten
der
Geraden q:
?2
so
daß
th
(Je ex)
•
(Je e3)
•
A
F^3]
(Je «,')
=
(Je e3')
=
*
m\
th
th
Al
*'^'
~
^-
=
taa
(t ct)
=
konst.
=
th2
(Je c2)
=
konst.
^33
A.^
Wir bezeichnen die Schnittpunkte der beiden Geraden p und q mit irgend
„konjugierte Achsenpunkte." Wir erhalten solche als Schnittpunkte der
jugierter Geraden in Bezug auf eine konfokale Schar mit einer Achse oder
punkte von Tangenten und Normalen in den Punkten eines Kegelschnittes.
als
einer Achse
Paare kon¬
als Schnitt¬
Salz 55: Das Produkt der hyperbolischen Taugens der Abstände zweier konjugierter
Achsenpunkte vom eigentlichen Mittelpunkt ist konstant, nämlich gleich dem Quadrate des
hyperbolischen Tangens der Entfernung der Brennpunkte dieser Achse vom Mittelpunkt.
Für die X3 ergibt sich eine andere Deutung:
Das Lot vom eigentlichen Mittelpunkt 03 auf die Gerade p hat die Gleichung:
tj3 xl
Ist
ß
Ist
ß'
—
rjj x2
=
der Winkel, den dieses Lot mit der Achse ox
Vll' + V
der
Winkel,
den das Lot
von
0
bildet,
so
ist:
VV + 7]32
03
auf q mit ot
ctg ß'
=
X3'
bildet,
Th
so
ist:
44
und somit:
(8)
ctg ß
•
ctg ß'
-*'^*-4»L
=
konst.
Analytische Geometrie der
gilt der
Satz 56: Das Produkt der Cotangens der Phasen konjugierter Geraden in Bezug auf
konfokale Schar oder von Tangenten und Normalen in den Punkten eines Kegelschnittes
Bezeichnen
wir
die
Winkel
ß, ß'
Euklidischen Ebene als die „Phasen"
eine
=
in
Anlehnung
an
der Geraden p, q.
die
Dann
ist konstant.
Wir
geben noch einige Sätze, die sich durch duale Betrachtungen wie
konjugierte Durchmesser ergeben:
57: Alle Paare konjugierter Achsenpunkte liegen harmonisch zu
die
entsprechenden
Sätze über
Satz
den beiden Brenn¬
der betreffenden Achse.
punkten
Satz 58: Die einer
Asymptote entsprechenden Leit-
und
Asymptotenpunkte
bilden ein
konjugierter Achsenpunkte.
Paar
Wir
erkennen
nichts anderes als
nunmehr
auch
das
Brennpunkte, die
konjugierter Achsenpunkte sind. Sie
Involution hyperbolisch oder elliptisch ist, d.h.
Kriterium
für
die Kealität
der
der Involution
die
Doppelpunkte
imaginär, je nachdem diese
Satz 59: Die Brennpunkte einer Achse eines Kegelschnittes sind reell oder imaginär,
die Mittelpunkte dieser Achse die Punkte eines jeden Paares konjugierter
nachdem
je
Achsenpunkte nicht trennen oder aber sie trennen. Bei den konkaven Ellipsen und konvexen
Hyperbeln sind die Brennpunkte einer einzigen Achse reell; die konkave Hyperbel und die
konvexe uneigentliche Ellipse dagegen besitzen 3 reelle Brennpunktepaare.1
Aus diesen Tatsachen folgt eine neue Lösung der Aufgabe, den Berührungspunkt einer
gegebenen Tangente zu finden, wenn ein Paar von Brennpunkten gegeben ist. Wir be¬
stimmen zum Schnittpunkt der Tangente mit der Achse der Brennpunkte den konjugierten
Das Lot von demselben auf die Tangente ist die Normale des
Punkt auf dieser Achse.
Punktes, trifft also die Tangente im gesuchten Berührungspunkt.
Wir wählen als Punkt eines Kegelschnittes, in welchem wir Tangente und Normale
einen Scheitel. Der Schnitt¬
zur Bestimmung konjugierter Punkte der Achse konstruieren,
Die
mit
dem Scheitelpunkt.
fällt
dann
Achse
zusammen
mit
der
der
punkt
Tangente
Normale hingegen schneidet die Achse, mit der sie zusammenfällt, im sog. Krümmungs¬
mittelpunkt. Derselbe läßt sich somit leicht konstruieren. Für die Entfernung desselben vom
eigentlichen Mittelpunkt finden wir, wenn wir beispielsweise einen Scheitel auf o2 wählen :
sind also reell oder
welche
Beziehung
in der Euklidischen Geometrie die Formel
031=
—
a
ergibt.
Die
1
Erörterungen dieses §
Vgl.
M. Zacharius:
a. a.
0.
lassen sich fast unverändert auf die Euklidische Geometrie
S. 40.
45
hyperbolischen Tangens der mit k multiplizierten Abstände
treten die Abstände selber.
Gleichung (8) nimmt die Form an:
1.
ctg ß ctg ß«
d.h. die Lote vom Mittelpunkt auf die zueinander senkiecht stehenden Geraden p, q bilden
übertragen.
An Stelle
der
=
•
-
selber einen rechten Winkel
§
Aufgabe
Konstruktionen
9.
Gegeben
14:
die auf der einen
liebigen
Punkt P.
sei ein
derselben,
von
Asymptoten
Kegelschnitt
und
Brennpunkten.
durch seine beiden
z. B. auf o2 befindlichen
Man konstruiere die Asymptoten
Achsen olt o2,
S' und einen be¬
eigentlichen
Scheitelpunkte S,
h2, h2', die zu o2 normal
stehen.
Losung: Auf Grund des Pascal'schen Satzes bestimmen wir erst die Tangente t des
gegebenen Punktes P (siehe Fig. 17). Durch Spiegelung an der Achse o1 erhalten wir
einen zweiten Punkt P samt Tangeute f. Auf den Tangenten bestimmen wir die zu P, P
orthogonalen Punkte N, N' als absolute Pole der Normalen n*, n"" in P, P. Die Paare
von
Verbindungslinien OiP, OsN, O^P, 03N' bilden eine Strahleninvolution, deren
46
Doppelstrahlen die gesuchten Asymptoten h2, h2 sind. Da der Träger der Strahleninvolution
ein uneigentlicher Punkt ist, schneiden wir das Strahlenbüschel mit der Achse o2 und
erhalten
dieselbe
auf dieser eine Punktinvolution mit einem
von
irgend
einem Hilfszentrum Z aus,
strahleninvolution o2 in seinen
Da
Schnittpunkten
so
mit
eigentlichen Träger. Projizieren wir
Doppelstrahlen dieser Hilfs7j2, A2'.
treffen die
P, P orthogonalen oder konjugierten Punkte N, N' in jedem Fall
uneigentliche Punkte sind, so müssen wir sie in der Konstruktion durch eigentliche
Elemente ersetzen. Die Normalen n*, nl* in P, P sind die absoluten Polaren von N, N',
die Schnittpunkte N*, N'* von n* und n'* mit
o2 sind die absoluten Pole der Verbindungs¬
linien
stehen,
w
nun
die
zu
und n'
02N'; die Geraden n*, n'*, die in N*, N'* auf o2 senkrecht
absoluten Polaren der Punkte N, N', d. h. der Schnittpunkte von n, n'
Die Verbindungslinien des Hilfszentrums Z mit den Punkten N,_ N', die der Punkt¬
=
sind
02JV
=
die
mit o2.
involution auf o2 angehören, stehen also auf den Loten zur Achse in den Schnittpunkten
der Kurvennormalen n*, n'* senkrecht.
Statt der Schnittpunkte von h2, h2 mit o2 lassen
47
Asymptoten punkte jBT2*, H2'* konstruieren: es sind die Schnittpunkte der
gemeinsamen Lote hz*, h2'* der Verbindungslinien ZH%, bezw. ZH^' mit o2.
Wir haben diese direkte Konstruktion der Asymptoten durch einen uneigentlichen
Mittelpunkt gewählt, weil ein solches Paar von Asymptoten immer reell existiert, und weil
diese Art der Lösung auch angewendet werden kann für die Konstruktion der Asymptoten
einer Semihyperbel, welche keinen reellen eigentlichen Mittelpunkt besitzt.
Aufgabe 15: Die Asymptoten eines Kegelschnittes zu konstruieren, von welchem der
Mittelpunkt und drei beliebige Punkte gegeben sind.
sich eventuell die
Lösung: Wir verbinden die drei Punkte A, B, G durch gerade Linien a
BC, 6= CA,
AB (siehe Fig. Ï8), bestimmen die Mittelpunkte Ma, Ma*; Mb, Mb*; Mc, Mc* der
Seiten des Dreiecks ABG.
Die Geraden 03Ma, 03ilfa*; 03Mb, 03Mb*; 03MC, 03MC*
—
c
3
=
stellen 3 Paare
konjugierter
Durchmesser dar.
Die Durchmesser nach den
Punkten Ma*, Mb*, Mc* stehen senkrecht auf den Mittelloten
Dreiecks.
Die
Asymptoten
Die Konstruktion wird
liegen, z.
Mittelpunkte der
messer
B. A und
Seiten in
daß die Durchmesser
ma,
mb,
uneigentlichen
mc der Seiten
des
sind die
Doppelstrahlen der Involution konjugierter Durchmesser.
unmöglich, wenn zwei der gegebenen Punkte auf einem Durch¬
G. Es fallt dann 03 mit Mb zusammen, und es liegen je drei
gerader Linie, nämlich Ma, Mb, Mc*, ebenso Mb, Mc, Ma*, so
03Ma, 03MC* und auch 03MC, 03Ma* identisch werden (siehe Fig. 19).
48
Der Beweis
hiefür
kann
einfachsten
am
auf
Weise erbracht werden:
folgende
(Anmerkung
S. 17) finden wir, wenn die Koordinaten von A, B, G mit
werden, für die Koordinaten von Ma, Ma*; Mb, Mb*; Mc, Mc*:
Ma:
o
ui
Mb'
a
vt
j|fc:
oeo,=
wzz
•
u>xx
•
=
=
•
et.
Ma*\
a
u,'
•
Xt,
Mb*:
a
v{
=
œxx
yt,
Mc*: oui,1
=
w^
yi H- Wyy
zt
-f-
wzz
<j)jj -Xi-{-iûxx
•
=
to**
•
•
yt
#/
—
—
•»/—
Nach
§
1
#,-, yt, zt bezeichnet
wyy
cd«
w**
•
•
•
zt.
#,-.
Vi-
Nun ist aber:
«/ *«/
«/'
#/
womit
unsere
eigentlichen
stehen.
Mittellote
Satz 60: Die
—
—
«// *>/
si ivt
+ •?,-
«>/
=
0,
=
0,
Natürlich
liegen auch die Punkte Ma, Mc, -M**
uneigentlichen Seiten-Mittelpunkte die absoluten Polaren der
muß also beispielsweise die Gerade MaMb auf mc senkrecht
so
sind,
somit den folgenden elementargeometrischen
Da
Wir -erhalten
«/<• «/
bewiesen ist.
Behauptung
auf einer Geraden.
—
die
Verbindungslinie
zweier Seitenmitten eines Dreiecks steht senkrecht auf
dem Mittellot der dritten Seite.
Für die Theorie der
obigen Überlegungen
Kegelschnitte
in der
hyperbolischen Geometrie ergibt
sich
aus
den
der
Satz 61: Verbindet
man
einen
beliebigen
Punkt eines
Kegelschnittes
mit den Schnitt¬
punkten eines beliebigen Durchmessers mit dem Kegelschnitt, so sind die durch die Sehnen¬
mittelpunkte gehenden Durchmesser konjugiert.
Aus den Formeln für die Koordinaten der Seitenmittelpunkte ist auch zu ersehen, daß
die drei uneigentlichen Mittelpunkte Ma*, Mb*, Mc* ebenfalls auf einer Geraden liegen.
Es müssen sich daher auch ihre absoluten Polaren, die Mittellote ma, nib, mc in einem
Punkte schneiden, womit ein neuer Beweis des Schnittpunktes der Mittellote eines Dreiecks
gegeben ist. Da das Lot im Mittelpunkt einer Seite senkrecht steht auf der Verbindung
der beiden andern
Dreiecks der
Seitenmitten,
so
stellen die Mittellote des Dreiecks ABC die Höhen des
Seitenmittelpunkte Ma, Mb, Mc dar,
In der Nicht-Euklidischen Geometrie
ist die
so
daß auch der Höhensatz bewiesen ist.
Figur
des Dreiecks mit seinen 6 Seiten¬
Figur des Dreiseits mit seinen 6
Aufgabe
Mittelpunktskegelschnitt sei gegeben durch
angehörige Scheitelpunkte S, S' und eine beliebige Tangente. Man
mittelpunkten vollständig
16:
punkte dieser
dual der
Ein
Winkelhalbierenden.
zwei
derselben Achse
konstruiere die Brenn¬
Achse.
Lösung: Wir ermitteln
Berührungspunkt der Tangente mit Hilfe des Satzes
Berührungspunkt und spiegeln alles
senkrechten
Achse (siehe Fig. 17). Die
der
der
beiden
zur
an
Scheitelpunkte
Verbindung
Normalen
Paare
schneiden
die
beiden
von Tangenten und
gegebene Achse in zwei Paaren
konjugierter Achsenpunkte, Punktepaaren der Brennpunktsinvolution, deren Doppelpunkte
die gesuchten Brennpunkte sind.
Aufgabe 17: Von einem Kegelschnitt seien gegeben: eine eigentliche Achse und drei
beliebige Tangenten. Es sollen die Brennpunkte der gegebenen Achse bestimmt werden.
von
Brianchon.
zuerst den
Sodann zeichnen wir die Normale im
49
Lösung: Sind (siehe Tig. 20)
dieselben untereinander
die drei Paare
von
Achse
gegebene
Brennpunkte
Die
in
h,
c
den Punkten
Winkelhalbierenden
Punktepaaren
gegebenen Tangenten,
(ab)
A=(bc), B=(ca) C
die drei
=
iva,
wa';
iVb,
der Involution
toi,';
wc,
wc'.
so
schneiden wir
und konstruieren
Dieselben schneiden die
konjugierter Achsenpunkte,
so
daß
die
sich konstruieren lassen.
Konstruktion
symmetrisch
in
a,
wird
unmöglich,
wenn
zwei
der
gegebenen Tangenten
zur
Achse
sind.
d;
O,
v
§
10.
Die
—
Semihyperbel.
vorangehenden Paragraphen besprochenen Eigenschaften, die stets für
Mittelpunktskegelschnitte abgeleitet wurden, übertragen sich zum großen Teil auch auf die
Semihyperbel mit unwesentlichen Modifikationen, die vor allem darin bestehen, daß eine
der beiden Asymptoten immer eigentlich, die andere uneigentlich und also bei allen Kon¬
struktionen zu ersetzen ist durch den entsprechenden eigentlichen Asymptotenpunkt, daß
gleicherweise der eine der beiden Brennpunkte dieser Achse ein eigentlicher, der andere
dagegen ein uneigentlicher Punkt ist und daß wir statt des letzteren die zugehörige eigent¬
liche Brenngerade verwenden. Es sind aber beide Asymptoten, wie auch beide Brennpunkte
reell. Naturgemäß fallen die Sätze dagegen weg, welche sich speziell auf den eigentlichen
Die
in
den
7
50
Mittelpunkt
eines
weise der Satz
Es
gibt
Kegelschnittes
Tom
ein
beziehen.
konstanten Dreieck
System konjugierter,
So wird für ein
eigentliches
Wesen
beispiels¬
bedeutungslos.
achsennormaler
Achsenpunkte.
Wir geben ein Beispiel einer Konstruktion,
um
Durchmesser, ein solches konjugierter
die
Anwendung
der Sätze
zu
zeigen.
Kegelschnitt sei bestimmt durch die Achse, einen Scheitelpunkt auf
Man konstruiere die Brennpunkte, die Asymptoten,
derselben und zwei beliebige Punkte.
die Leitlinie und den Leitpunkt.
Lösung: Es sei S der gegebene Scheitelpunkt auf der Achse o2, A, B seien die beiden
andern Punkte. Da wir die Tangente in S als Lot zu o2 sofort zeichnen können und durch
Spiegelung an der Achse o3 noch mindestens einen weiteren Punkt 0 (in Fig. 21 z. B. ist
0 der symmetrische Punkt zu A) erhalten, so ist der Kegelschnitt vollständig bestimmt
und der Satz von Pascal liefert uns dann auch noch die Tangenten t, r in den nicht
Aufgabe
18: Ein
symmetrischen Punkten A, B. Zu diesen ermitteln wir noch die Normalen. Es seien
sodann A, B die Normalprojektionen der Punkte A, B; T, B die Schnittpunkte der
51
Tangenten t,
Lote
zu
Figur
o2 in
mit o2; M*, N* diejenigen der Normalen m*, n* in A, B;
M*, N*. Ziehen wir nun von einem beliebigen Hilfszentrum aus
r
eingezeichnet ist)
nicht
senkrecht
zu
n*,
Strahlenpaare
die
nach:
erhalten wir eine Strahleninvolution
so
punkte
das
Brennpunkte
eigentlichen Brennpunkt F
Gerade g, so liegt der Pol von
schnitt Je einerseits auf der Polaren
auf der
6-
von
Tangente
r
r
Doppel¬
deren
auf o2 sind.
Verbinden wir den
mit B durch eine
in der
B und
zu
strahlen o2 in ihren Schnittpunkten mit den Asymptoten treffen.
Die Punkte T, M*; B, N* sind Punktepaare einer Punktinvolution,
die
(das
m*,
Hilfszentrum, deren Doppel¬
senkrecht
A und
um
m*, n* die
gegebenen Punkte, z. B.
Bezug auf den gesuchten Kegel¬
mit einem der
g in
F, der Leitlinie, die
von
in B und endlich noch auf dem Lot i
mit i ist ein Punkt der Leitlinie
zu
zu
ist, anderseits
bestimmen
g in F.
Der
Schnittpunkt
l, die damit bestimmt ist.
Brennpunkt F mit einem der Endpunkte W der eigent¬
lichen Asymptote Ji, so
Halbierungslinie des Winkels WF8 die Scheiteltangente s
in ihrem Schnittpunkt mit der Tangente w von W an den Kegelschnitt. Ihr Schnittpunkt
Da die
mit o2 ist der gesuchte Leitpunkt L, der der eigentlichen Asymptote entspricht.
beiden Brennpunkte, die Asymptoten und. also auch die Asymptotenpunkte schon bekannt
sind, lassen sich die beiden Leitpunkte auch konstruieren als vierte harmonische Punkte
zu ihren entsprechenden Asymptotenpunkten in Bezug auf die beiden Brennpunkte.
Analog
Verbinden wir zuletzt
den
trifft die
hätten auch die Leitlinien bestimmt werden können.
Es existiert ein Büschel homothetisch'er
(1)
Jcxx
einer
=
k2 an
die
Gleichung
des
Koordinatensystems hat,
in der Form
(2)
Icxx
Semihyperbel,
geschrieben
X (ùxx
—
Setzen wir #2
=
0,
x^ -J-
=
so
k2
so
x22
—
2
ka13
=
0
Scheitel im Punkte xx
die ihren
kann die
x1 x3
eigentlichen
Gleichung einer jeden
nomothetischen
(au
—
X) x^ -j-
erhalten wir die
—
X)x1*
Je2
(a22
X) x2s
—
Gleichung
—
2 h als
—
2 Je a13 xx x3
der beiden
x1x3JrX x32
-f-
X
x32
(4)
w^
die
(5)
k2 x2
=
+ k2 x2
erfüllt ist,
was
für X
0
Semihyperbel
—
x32
=
=
0.
von
Geraden
0
Bedingung
—Ä*^ —X) +
=
=
0
Invariantentheorie lehrt, daß der zerfallende Kegelschnitt (3) ein Paar
darstellt, die in Bezug auf den A. K.
wenn
0, x2
Scheiteltangenten:
=
Die
konjugiert sind,
=
werden:
Je2 (an
(3)
&! a22
Ist
Semihyperbeln.
^an der
fc*X
=
0
Fall ist.
Satz 62: Jedes Büschel homothetischer
Semihyperbeln
enthält eine
einzige parabolische
Hyperbel.
Es
gibt
auch eine Schar konfokaler
Satz 63: Jede Schar konfokaler
Semihyperbeln.
Semihyperbeln
Für dieselbe
enthält eine
gilt
der
analoge
einzige parabolische Hyperbel.
52
III. TEIL.
Sätze und Konstruktionen für
1.
§
Die
spezielle Kegelschnitte.
parabolische Hyperbel.
Wählen wir die reelle Achse und die beiden
so
läßt sich die
parabolische Hyperbel
(1)
oder
Jcxx
wenn
=
Jcxx
.
Hieraus und
aus
der
=
Gleichung
(3)
x22
erhalten wir die
Gleichung
—
2 h a13 x± x3
=
0,
Die Koordinaten der
H
(5)
:
E':
2kp'X1x3
]c2x12-lrlc2xi2
xx2 -\-
x3'i
—
x1 x3
'
—
L
Asymptoten
x32
0,
=
ergeben:
h:
Jcx1 +
(p-\/l-\-p2)x3
=
0,
*^ + (p +VI+*")*,
=
0;
Schnittpunkte
=
—
xx
=
-
(p
V
—
(p +
von
h, V mit der Achse sind :
+i>2),
oci
=
0, x3
=
Je.
VTTi2),
x3
=
0,x3
=
h.
1
VT+F2,
x^p + Tjl+p2,
H'*: xt =p
L^H*:
Satz 64:
0
h':
x1
=
=
sich
Bestimmen wir noch die Koordinaten der Leit- und
(6)
0.
=
Asymptotenpaares:
2 kp
der einzelnen
(4)
—
des A. K.
des reellen
h2
Gleichungen
k2x2z
=
wxx
die
durch die
wir a13=paM setzen und durch a2S dividieren:
(2)
woraus
k2 aM
Scheiteltangenten als Koordinatenachsen,
Gleichung darstellen:
-
Asymptotenpunkte;
x2
==
0, x3
x2
=
0, x3
Der einer
Asymptote entsprechende Leitpunkt
Asymptote und umgekehrt (siehe Fig. 22).
Weiter gilt der
=
=
so
finden wir:
k.
k.
ist der
Asymptotenpunkt
der
andern
Asymptote und zugehöriger Leitpunkt haben gleichen Abstand von jedem
Scheitelpunkte (siehe Figur).
Gleichung der parabolischen Hyperbel und des A. K. in Linienkoordinaten lauten:
Satz 65:
der beiden
Die
(7)
Ks
QK
(8)
Die beiden
Brennpunkte
=
=
pl,'-2H1^
=
Ç1" + Çï,-*,Ç,,
der Achse sind
gegeben
p^-\-2H1l3-lc2pl32
oder durch die
(9)
0
=
0
durch die
=
0
l
Gleichungen:
—VT+7«)ç,
=
o
F':p1;1+k{l + \l+p>)S3
=
0
Fip^ + Mi
Gleichung:
53
woraus
*
sich die Koordinaten
'
Für die Leit- und
(H)
ergeben:
F:
ax1=p, aa3
-F':
0^=?, az2
Brenngeraden
0, ax3
=
Je(1
=
0, oic3
=
J;(l + Vl+/).
finden wir die
—
Gleichungen:
l
=/'*:
fe(l—Vl+l>,)a;1+i>a?8
=
0
V
=
f*:
Ä(l + VT+F)*i+**»
=
<>
v„
oa-
VT+p).
=
/
-4^
Ä^-,
dtf
H
ÏVyS'-O,
/
/
/
Fig.22.
Satz 66: Die zu einem Brennpunkt gehörige Leitlinie fällt mit der dem andern Brenn¬
punkt entsprechenden Brenngeraden zusammen (siehe Fig. 22).
Durch Vergleichung der Koordinaten des Schnittpunktes der Leitlinien mit der Achse
mit denjenigen der Brennpunkte ergibt sich
Satz 67: Brennpunkt und zugehörige Leitlinie sind gleich weit entfernt von jedem der
beiden Scheitelpunkte (siehe Fig. 22).
Die Sätze 65 und 67 sind spezielle Fälle des folgenden:
Satz 68: Die Tangente in einem Punkt einer parabolischen Hyperbel Schneidet die
Achse in einem Punkt, der vom Scheitelpunkt gleiche Entfernung hat wie die Normal-
54
Projektion des Berührungspunktes. Oder: Jede Normale zur Achse hat zum Pol in Bezug
auf die parabolische Hyperbel denjenigen Punkt der Achse, der zum Schnittpunkt des Lotes
mit der Achse symmetrisch ist bezüglich des Scheitelpunktes der Kurve.
Die Gleichung der Tangente £
Bciveis: Es sei P (yv y2, y3) ein Punkt der Kurve Je.
in P lautet:
hp y3 xx
Für den
Schnittpunkt
T der
—
¥ yt xt -\-'k$y1xz
Tangente
mit der Achse
=
ergibt
§
sich:
*
2/3*1+2/1^3=°
oder:
&1==
2/1
»
X3== y3
'
des Lotes mit der Achse ist.
Schnittpunkt
03 Q,
Eigenschaften der allgemeinen Kegelschnitte übertragen sich auch auf die speziellen,
wenn wir die Begriffe „Achse" und
„Mittelpunkt" sinngemäß anwenden.
Satz 31 ergibt, auf den uneigentlichen Brennpunkt der parabolischen Hyperbel an¬
gewendet, den
also
03
T=
wenn
Q
der
Die
Berührungspunkten zweier Tangenten mit einer parabolischen
Hyperbel Lote auf die Leitlinie, so wird die Strecke zwischen den Lotfußpunkten halbiert
durch die Projektion des Schnittpunktes der beiden Tangenten (siehe Fig. 23).
Satz 69 : Fällt
Speziell gilt
man von
den
der
Projektion der Strecke, die auf einer Tangente einer parabolischen Hyperbel
begrenzt ist durch den Berührungspunkt einerseits und den Schnittpunkt der Tangente mit
der Achse anderseits, auf die Leitlinie wird halbiert durch die Projektion des Schnittpunktes
der Tangente mit der Scheiteltangente (Fig. 22).
Es ergeben sich mehrere Lösungen der
Aufgabe 19: In einem gegebenen Punkt einer parabolischen Hyperbel die Tangente
Satz 70
zu
:
Die
zeichnen.
1: Tragen wir (siehe Fig. 22) die „Abszisse" 03Q des gegebenen Punktes P
Scheitelpunkt 03 aus nach der andern Seite auf der Achse ab und erhalten so den
Schnittpunkt T der Tangente mit der Achse.
Lösung 2: Ist (siehe Fig. 22) der eigentliche Brennpunkt F gegeben, so ziehen wir
demselben
den Brennstrahl nach dem gegebenen Punkt Pund halbieren den Winkel 03FP.
von
Die Winkelhalbierende trifft die Scheiteltangente in ihrem Schnittpunkt E mit der gesuchten
Tangente. (Die Winkelhalbierungslinie des Nebenwinkels geht durch den Schnittpunkt
der Tangente mit der uneigentlichen Scheiteltangente.)
Lösung 3: Fällen wir (Fig. 22) vom gegebenen Punkt P das Lot auf die Leitlinie l
und konstruieren wir das Mittellot der Strecke zwischen dem Lotfußpunkt P und der Achse,
so trifft dasselbe die Scheiteltangente ebenfalls im Punkte R.
Lösung 4: Ziehen wir den Brennstrahl s nach dem gegebenen Punkt P und errichten
wir auf demselben im Brennpunkt das Lot r, so geht die gesuchte Tangente durch den
Schnittpunkt des Lotes mit der Leitlinie (siehe Fig. 23).
Aufgabe 20 : Es soll der Berührungspunkt einer Tangente konstruiert werden.
Lösung
vom
55
Scheitelpunkt der Kurve gegeben, so tragen wir die durch
die
auf der Achse abgeschnittene Strecke Oa T vom Scheitelpunkt auf die andere
Dasselbe geht durch den
Seite ab und errichten im Endpunkt Q das Lot zur Achse.
P
der
Tangente.
gesuchten Berührungspunkt
Losung 1
Tangente
Losung
binden
Ist
(Fig. 22)
2. Kennen -wir bereits den
wir
(siehe Fig. 22)
und
tangente
tiagen den
Der zweite Schenkel
Losung
der
3:
geht
Wir fällen
F mit
Winkel
dem
Brennpunkt F der parabolischen Hyperbel, so ver¬
Schnittpunkt H der Tangente mit der Scbeitel-
03FR
vom
die Gerade FE nach
an
Berührungspunkt
Schnittpunkt der Tangente
dann durch den
P der
der andern Seite
Tangente
Scheiteltangente
mit der
an.
mit der Kurve.
das
Leitlinie, verdoppeln die von der Achse aus gemessene Strecke auf der
PP zur Leitlinie; dasselbe geht
neuen Endpunkt P das Lot
durch den gesuchten Berührungspunkt (siehe Fig. 22).
Losung 4: Schneiden wir die gegebene Tangente mit der Leitlinie und verbinden wir
den Schnittpunkt mit dem Brennpunkt F, so geht das Lot im Brennpunkt zur Verbindungs¬
Lot RR auf die
Leitlinie und errichten im
linie FS durch den
Berührungspunkt
P der
Tangente (siehe Fig. 23).
56
Berechnen wir die Abstände eines
Hyperbel
von
einem
beliebigen Punktes P (yv yt, y3) einer parabolischen
Vi -\-p2)~\ und von der zugehörigen Leitlinie
Brennpunkt F [p, 0, k (1
—
t(l-Vl+P,)aJ1+l»*B
so
(h
cw
•
PF)=
ta*
-
0,
Durch eine kurze
Q- -^11+P2) y^
(k2 y2+F^-2/32).(-2+2Vl +2>2)
(* V + k2 y2
es
=
finden wir:
Rechnung
-
y2) ('
finden wir die
Beziehung:
ch2
sh2
(k PF)
•
—
+2 V
2
(k PT)
•
=
1
+ P2)
1,
muß also PF=Pl sein.1
Satz 71
punkt
und
:
Die Punkte einer
von
parabolischen Hyperbel
haben
gleichen
Abstand
vom
Brenn¬
der Leitlinie.
geometrische Ort aller Punkte, die von einem festen Punkt und einer
gleichen Abstand haben, ist eine parabolische Hyperbel, für welche der
gegebene Punkt Brennpunkt, die gegebene Gerade Leitlinie ist.
Satz 72:
Der
festen Geraden
Da Satz 26 auch für die
Satz 73:
der
Kurve,
so
Satz 74: Verbindet
umhüllen
parabolische Hyperbel gilt, folgt:
Spiegelt
Brennpunkt einer parabolischen Hyperbel
alle
Spiegelpunkte auf der Leitlinie.
liegen
man
den
man
die Mittellote
an
allen
Tangenten
gegebenen Geraden,
parabolische Hyperbel,
einen festen Punkt mit allen Punkten einer
aller
eine
dieser
Verbindungsstrecken
gegebenen Punkt zum Brennpunkt und die gegebene Gerade zur Leitlinie hat.
Hieraus ergeben sich neue Lösungen der Aufgaben 19 und 20.
Denken wir uns von einem beliebigen Punkt außerhalb der parabolischen Hyperbel an
dieselbe eine Tangente gezogen und verbinden wir den gegebenen Punkt mit dem Brenn¬
punkt und mit dessen Spiegelbild in Bezug auf die Tangente, so müssen diese beiden Ver¬
so
welche den
bindungslinien gleich lang
sein und mit der
Daraus entnehmen wir die
Tangente
auch noch
gleiche
Winkel bilden.
Lösung der
Aufgabe 21: Von einem Punkt außerhalb einer parabolischen Hyperbel, von welcher
Brennpunkt und Leitlinie bekannt sind, die Tangenten an die Kurve zu zeichnen.
Lösung: Wir schlagen um den gegebenen Punkt einen Kreis, der durch den Brenn¬
punkt geht. Wir verbinden dann die beiden Schnittpunkte dieses Kreises mit der Leitlinie
mit dem gegebenen Punkt. Halbieren wir hierauf die Winkel, die diese Verbindungslinien
mit der Geraden PF bilden, so sind die Winkelhalbierungslinien die gesuchten Tangenten vom
Punkte P an die Kurve (siehe Fig. 24).
Der von den Tangenten t, t' eingeschlossene Winkel TPT ist gleich | <( SPS'. Fällt P
auf die Leitlinie, so wird <[ SPS'
n, es ist also der von den beiden Tangenten gebildete
=
Winkel ein rechter.
1
Vgl. W.Killing:
a.a.O.
S
12.
57
Satz 75: Der
geometrische Ort der Punkte, von welchen an eine parabolische Hyperbel
Tangenten sich ziehen lassen, besteht aus den beiden Leitlinien der
parabolischen Hyperbel.
Weiter ergibt sich, wenn P ein Punkt der Leitlinie ist, daß die Strecke SS' gleich
der doppelten Entfernung PF ist.
zueinander senkrechte
der
Satz 76: Die Projektion einer Sehne durch
doppelten Entfernung ihres Poles in Bezug
den
Brennpunkt auf die Leitlinie ist gleich
parabolische Hyperbel vom Brenn¬
auf die
punkt.
Berechnen wir
gleicherweise die Abstände einer gegebenen Tangente von der Asymptote
zugehörigen Leitpunkt. Die Gleichung der Tangente in einem Punkte P (ylt y2, y3)
parabolischen Hyperbel lautet:
und dem
einer
kp t/s
diejenige
der
Asymptote
Daraus
ergibt
—
£2 !ft #2
+ kp yx
x3
=
0,
h:
.
Die Koordinaten des
xi
»!»1 +
(p-VT+7«)a:3
zugehörigen Leitpunktes
=
0.
haben die Werte :
(p
—
Vi-)- p2), 0,
sich:
8
k.
58
*>
\h. (t, »)]
(ft» j>' y32 +
V
Hieraus
folgt
tyyy.-*,i»(p-Vi + p,)yJ
=
fc*
y,'
(fcV & + **&
die
-
—
fcV yt2)
(-
2
^^_
Fj? V1H- i>2)
Gleichung:
•
(t, h)
2
tfptyfl'i— 2k2p2-t-2k!!pVl + p2)
eh2 ßfc (*, A)]
sA2 pt (J, L)~]
(t, L).
Satz 77: Jede Tangente einer parabolischen Hyperbel
Asymptote wie vom zugehörigen Leitpunkt.
Also ist:
fcV +
=
•
—
1
—
hat
gleichen
Abstand
von
der
Satz 78: Alle Geraden, die von einer gegebenen Geraden und einem gegebenen Punkt
gleichen Abstand haben, umhüllen eine parabolische Hyperbel, welche die gegebene Gerade
zur Asymptote und den gegebenen Punkt zum Leitpunkt hat.
Daraus folgt weiter:
Satz 79: Spiegelt man die Asymptote an allen Punkten einer parabolischen Hyperbel,
so gehen alle Spiegelbilder durch den Leitpunkt.
Satz 80 : Zieht man durch einen gegebenen Punkt eine Gerade und bestimmt man das
gemeinschaftliche Lot derselben mit einer andern gegebenen Geraden, so ist der geometrische
Ort des Mittelpunktes dieses Lotes eine parabolische Hyperbel, für welche die gegebene
Gerade Asymptote, der gegebene Punkt Leitpunkt ist.
Diese Sätze liefern wiederum Lösungen für Aufgabe 19 und 20.
Aufgabe 22: Die Schnittpunkte einer Geraden mit einer parabolischen Hyperbel zu
konstruieren, wenn diese durch ihre eigentliche Asymptote und den zugehörigen Leitpunkt
gegeben ist.
Lösung: Wir konstruieren den Kreis, der die gegebene Gerade p zur Achse hat und
die gegebene Asymptote berührt.1 Vom Leitpunkt L ziehen wir die beiden Tangenten s, s'
Die gemeinschaftlichen Lote n, n' von s und Ji, bezw. von s' und h, wie
an den Kreis.
auch die Winkelhalbierenden (Mittelabstandslinien) dieser Geradenpaare treffen die gegebene
Gerade p in ihren Schnittpunkten mit der Kurve. Die Tangenten t, t' in diesen Schnitt¬
punkten T, T' von p mit Je ergeben sich auf folgende Weise : Wir errichten in L die Lote
Die Senkrechten durch 1, T' zu r, bezw. r' sind die gesuchten Tangenten
r, r' auf s, s'.
(siehe Fig. 25).
Die Untersuchungen über konjugierte Durchmesser und konjugierte Achsenpunkte lassen
sich ebenso durchführen, wie es in § 7 des IL Teiles für allgemeine Kegelschnitte geschehen
ist. Für die Abstandskoeffizienten zweier konjugierter achsennormaler Durchmesser finden
wir die Beziehung:
1
0, (X
k*l\'—lcp(\ + \')
xl'.xa)
ij1:îj3, \'
—
Setzen wir X
=
X',
so
ergeben
sich
Gleichungen
1
der beiden
Dändliker: a.a.O.
S. 1.
=
aus
x==
die
=
Asymptoten.
—p+Vi+p2
Tc
=
59
Für die
Punktepaare
konjugierter Achsenpunkte
der Involution
einzigen
auf der
reellen
Achse finden wir die Relation:
h*j?XX'
Für X
=
—
*(X + X')
X' erhalten wir die
—p
=
0,
wo
th(fte)
der beiden
Gleichungen
Der
=
X, fh(fte')
=
X'.
Brennpunkte.
konjugierte Punkt zum Scheitelpunkt (X
0) ist auch hier der Mittelpunkt des
Krümmungskreises in diesem Scheitelpunkt. Für seinen Radius ergibt sich die Formel:
=
th(Jc p) =-\-p.
(In der Euklidischen Geometrie : p =#.)
Die parabolische Hyperbel der hyperbolischen Geometrie
geht
•
Parabel über,
wenn
die
Maßbestimmung
in der Ebene
spezialisiert
in
die
Euklidische
wird.
Die
Asymptoten
fallen aber mit der unendlich fernen Geraden zusammen, ebenso fallen Leit- und
Asymptoten¬
punkte auf die unendlich ferne Gerade. Es fallen also die Sätze über Asymptoten, Leitund
Asymptotenpunkte
erhalten.
Die Lote
zur
Die Brennpunktseigenschaften
weg.
Leitlinie werden zur Achse parallel.
dagegen
bleiben
vollständig
60
2.
§
auf ein Polardreieck des A. K. w, dessen
Bezogen
(1)
¥x12-\-]c2x22
"
=
uxx
Parabel mit
jede
kann
(2)
Kxx
=
au *i
»
a22 x2
T*
=
ß22 ^2
n>
—
*
ß33 ^1 ^3
r
gemeinsame Gleichungsform
eine
x32
—
=
zu
:
werden durch die
==
Gleichung:
">
durch:
^33 Xî
erhalten,
dann lautet
0
an Xl X3
uneigentlichem Scheitelpunkt dagegen
Parabel mit
(OJ
Um
Gleichung
eigentlichem Scheitelpunkt dargestellt
Kxx
jede
Die Parabel.
==
*"
unterwerfen wir
der Koordinaten¬
(2)
transformation
(4)
Jcx1+x3
=
ax1',
Tcx1—%3
kx1-\-x3
(5)
=
axll,
Dividieren wir die entstehenden
kxx—x3
sich
(2)
aus
p,
Thfjf
(6)
während die
dieselbe
(3)
und
few
sich als
X ü)x,x.
-
Bedingung
p
p
(p
(p
—
—
1)
1)
des A. K.
=
(1
die
Gleichung
punkt
folgt
die
durch a22 und setzen wir
z2'a +
x,' x3'
2
-f- 2
(p
> 0 für Parabeln mit
<C 0 für Parabeln mit
2
=
-
0.
X) V x3' + 2p z3'2
—
-
2
Ç,' V
Çî" + 2Ç1,ÇB1
=
X
%,
=
2
V2
-
0» + X) ?2'2
die
=
zur
=
0
Achse
parallel
laufen :
0,
p
=
=
n
1 a22
,
-
2
0,
ergibt:
(1 + X) ?/ Ç,'
daß die Parabel außer dem
p <C 1 für Parabeln mit
gegebenen
=
der konfokalen Parabelschar sich
Bedingung dafür,
von
0
eigentlichem Scheitelpunkt,
uneigentlichem Scheitelpunkt.
l^-p l2'2
p > 1 für Parabeln mit
Mit Hilfe
=
Asymptoten,
für die Realität der
auf der Achse noch zwei weitere reelle
„.
ß33
—jï-=p,
2 a22
U
bezw.
:
Zpp
Daraus
1
Gleichung
X) x2'2
—
Oee
(12)
,
=
%,
woraus
aix2
der Parabel in Linienkoordinaten ist:
Gleichung
(10)
diejenige
(11)
=
des Büschels homothetischer Parabeln
Gleichung
(8)
Die
ax2\
des A. K. lautet :
Gleichung
u**
ergibt
=
\2kx2
ax3,
—
xtn -\-2px1'x3' + 2p x3'*
=
(7)
Aus der
=
Gleichungen
2 a22
ergibt
y 2kx2
ax3,
der Transformation
(3) hingegen
so
=
bezw. p
=
Kriterien für die verschiedenen
Brennpunkte
=
0.
einen, immer reellen Brenn¬
auf x3
=
0 besitze
:
eigentlichem Scheitelpunkt,
uneigentlichem Scheitelpunkt.
33
2 a22
ergeben
Parabeltypen.
sich die in
§
4 des I. Teiles
an-
61
geht eine Kurve eines Büschels homothetischer Parabeln,
das entweder aus lauter hyperbolischen Parabeln (siehe Fig. 26), oder aber aus lauter
elliptischen Parabeln besteht. Im ersten Fall enthält das System drei gemeinsame, reelle
und eigentliche Asymptoten, von denen zwei zur Achse gleichsinnig parallel sind, während
Im zweiten Fall hingegen existiert nur eine
die dritte Asymptote zur Achse normal ist.
Durch jeden Punkt der Ebene
reelle, aber uneigentliche achsennormale Asymptote. Ist ein Büschel homothetischer hyper¬
bolischer Parabeln gegeben, so wird jede Gerade, welche die beiden achsenparallelen
Asymptoten schneidet, von zwei konvexen hyperbolischen Parabeln berührt; jede Gerade»
welche keine der Asymptoten, wohl aber die Achse der Parabeln im Eigentlichen schneidet,
ist Tangente an zwei einteilige konkave hyperbolische Parabeln; jede Gerade endlich, die
Asymptote im Eigentlichen begegnet, berührt eine zweiteilige
einteilige konvexe hyperbolische Parabel, erstere in einem eigentlichen,
letztere in einem uneigentlichen Punkte.
Eine Schar konfokaler Parabeln besteht, wenn 3 reelle, aber uneigentliche Brennpunkte
(einer auf der Achse, die beiden andern auf der Tangente im Berührungspunkt der Parabel
mit dem A. E.) existieren, aus ein- und zweiteiligen konkaven hyperbolischen und uneigentweder der Achse, noch einer
konkave und eine
62
elliptischen Parabeln (siehe Fig. 27). Ist dagegen nur ein einziger Brenn¬
reell, so enthält die Schar eigentliche und konkave uneigentliche
punkt
konvexe
und
elliptische
hyperbolische Parabeln (siehe Fig. 28). Jede Gerade der Ebene
wird von einer Kurve einer konfokalen Schar berührt.
Durch jeden eigentlichen Punkt
der Ebene gehen zwei konfokale Parabeln, die sich rechtwinklig schneiden.
lichen konvexen
auf der Achse
NT
Fig.27.
/
Für eine Parabel, die
Form
(14)
(2) hat,
l2
konfokal
(X—an) (X
—
oder nach Potenzen
ist,
4 a22)
von
(16)
beliebig gegebenen Parabel, deren Gleichung
Gleichung in Punktkoordinaten:
X
etwa die
finden wir die
x?+h2 (X—2 a22fx22+4 fca22 (X
(15)
wo
einer
zu
—
an) xx x3
—
X
(X
—
an) x2=0
geordnet:
(i)«
•
\2—pxx
•
X-f- 4a22'hxx
=
Q
die Parabel
pxx
=
&2
(flu -|-
4
a22) xt2 -f-
2 lc2 a22
x22 -\-
4 £ a22 xx x3
—
an
x32
—
0
geometrischen Ort derjenigen Punkte darstellt, von welchen zwei zueinander senkrechte
Tangenten an die Parabel gezogen werden können. Analog zu § 4, II. Teil wollen wir die
Wurzeln X1( X2 der Gleichung (15), wenn in derselben xv x2, x3 die Koordinaten eines
den
63
gegebenen
Punktes bedeuten,
als
Zwischen denselben bestehen die
so
daß
jede
zur
gegebenen
»parabolische
Beziehungen:
Parabel homothetische Kurve als der
erscheint, für welche das Produkt ihrer
der Ort
Koordinaten"
parabolischen
Die in
Ort der Punkte
zu
pxx
==
ist, während
0 homothetischer
ist.
der zweiten Hälfte des
Brennpunkten
Asymptoten
zur Lösung der folgenden
und
Aufgabe
geometrische
Koordinaten konstant
aller Punkte mit konstanter Koordinatensumme ein
Kegelschnitt
dieses Punktes bezeichnen.
23: Von
§
6 des IL Teiles
dargelegten Beziehungen zwischen
übertragen und verwenden
lassen sich auch auf die Parabel
einer Parabel ist die Achse mit der
Brennpunkt gegeben, sowie ein beliebiger
absolute Brennpunkt der Achse und die zu
Punkt
samt
Kichtung nach dem absoluten
Tangente. Es sollen der nicht¬
ihr senkrechte
Asymptote
konstruiert werden.
64
Lösung:
Wir ziehen durch den
wollen
wir
im
gegebenen
Punkt T die Parallele TF'
eine Gerade
die
mit
zur
Achse
der Achse
—
den
verstehen,
folgenden
und spiegeln dieselbe an der ge¬
Brennpunkt F' als Ende gemeinsam hat
TF' trifft die Achse im gesuchten nicht¬
gebenen Tangente t. Das Spiegelbild s von s'
Die achsennormale Asymptote h ist das gemeinschaftliche Lot
absoluten Brennpunkt F.
zur Achse und derjenigen gemeinsamen Parallelen von s und s', die zur Tangente t senk¬
recht steht und zur Achse nicht im oben angegebenen Sinn parallel ist (siehe Fig. 29).
darunter
stets
absoluten
—
=
Aufgabe
24:
Man kennt den absoluten und den nichtabsoluten
Achse einer Parabel.
eine
Es soll die achsennormale
beliebige Tangente gegeben
Asymptote
Brennpunkt
konstruiert werden,
auf der
wenn
noch
ist.
Fällen wir
vom
absoluten
Brennpunkt
F' das Lot
gegebenen Tangente,
Endpunkt
Brennpunkt F
und fällt man vom neuen Endpunkt V der letzteren Verbindungslinie wiederum das Lot
auf die Tangente, so geht dasselbe durch den der gesuchten Asymptote entsprechenden
Asymptotenpunkt, die Asymptote selber ist also gemeinschaftliches Lot der Achse und der
Senkrechten vom Punkte V zur Tangente t. Die Verbindung UV begegnet der gegebenen
Tangente t in ihrem Berührungspunkt mit der Parabel.
Wäre statt der Tangente t der Berührungspunkt 1 gegeben, so würde sich durch
Lösung:
verbinden wir den andern
zur
TT des Lotes mit dem nichtabsoluten
65
Anwendung des Satzes 26 in § 4 des II. Teiles leicht die Tangente bestimmen lassen. Die
Aufgabe besitzt allerdings dann zwei Lösungen.
Aufgabe 25 : Den nichtabsoluten Brennpunkt der Achse einer Parabel zu konstruieren,
die Achse mit der Richtung nach dem Berührungspunkt mit dem A. K. und die
wenn
achsennormale Asymptote gegeben sind, sowie ein beliebiger Punkt der Kurve.
Lösung: Wir ziehen durch den gegebenen Punkt T die Parallele zur Achse und kon¬
struieren durch das andere Ende JJ' von TF' das Lot zur gegebenen Asymptote h. Es
treffe den A. K.
zum
zweiten Male in V.
Die Gerade TV schneidet die Achse im
gesuchten
Spiegelbild von TF' in Bezug auf die
oder die Kurvennormale n im gegebenen Punkt T, so daß sich gleichzeitig
auch diese beiden Geraden ergeben (siehe Fig. 29).
Ist an Stelle des gegebenen Punktes T seine Tangente t bekannt, so läßt sich die
Aufgabe ebenfalls lösen. Wir übergehen die Lösung aber.
Wenn wir uns die Frage nach den konjugierten Durchmessern vorlegen, so gehen wir
aus von der Tatsache, daß solche Kombinanteneigenschaft haben, d. h. daß ein Paar kon¬
jugierter Durchmesser in Bezug auf alle Kegelschnitte des Büschels nomothetischer Kegel¬
schnitte, dem ein gegebener Kegelschnitt angehört, konjugiert sind. Die Verhältnisse werden
Brennpunkt
Tangente t
F.
TV ist nichts
anderes
als
das
9
66
daher etwas
einfacher, wenn wir als Ausgangskegelschnitt einen solchen mit eigentlichem
Scheitelpunkt voraussetzen (siehe Fig. 30).
Bezogen auf ein Polardreieck des A. K., läßt sich die vorgegebene Parabel durch
Gleichung (2) darstellen, während der A. K. durch (1) gegeben ist. Die Koordinatentrans¬
formation (4) ergibt dann wieder Gleichung (6).
Die Polaren eines Punktes P, dessen
Koordinaten im alten System mit yt, ?/2, y3, im neuen mit «//, y2', y3' bezeichnet werden
mögen, haben folgende Gleichungen:
<>
(19)
py«V + y,'s,l+i»(yi, + 2y,,)*,'
(*>)
0
(20)
y.tmi' + y,'x,' + y1'xa'
(p*)
=
=
_
woraus
_
sich
die Beziehungen
(21)
ergeben:
(P- 1) ys'< + [(p-l)yi' + 2Pya'] -x3'
0,
(l-p)y2'xi' + 2pys'xs'
(22)
=
0
=
oder in alten Koordinaten:
(23)
k2
(24)
(2p
—
1)
y1 x1
:
=
X, x1
ys)
:
xt
=
+
—
kp (yt xs + yz xj + ysxa
=
0
0
p) y2x2—p (k y1
ys) xs
die
aus
:
(23)
geht
xz
Beziehung
ys
0
(25)
k2(2p-l) XX'— kp(X-\-X') + l
th (k- d') die Abstandskoeffizienten zweier kon¬
th (k d) und kX'
hervor, worin kX
jugierter achsennormaler Durchmesser sind. (23) und (24) stellen übrigens die konjugierten
Durchmesser zu den achsennormalen und achsenparallelen Durchmessern durch den gegebenen
Punkt P dar.
Wenn die Gleichung des letzteren im alten Koordinatensystem lautet:
0
ys'x2'-y2'xs'
(26)
im neuen System also:
0
y3)x2 + y2x3
(27)
kij2x1 + (ky1
und wenn wir mit 5, §' die senkrechten Abstände des Scheitelpunktes von diesem Durch¬
messer und den konjugierten, gegeben durch (24), berechnen, so finden wir die Werte:
kp(ky1
Setzen wir y1
—
k2
X',
(1
—
—
=
so
=
=
•
=
=
=
—
—
A(i.s)=_^_, Ä(4.,)=fÄ^.
(28)
^
woraus die
Beziehung folgt:
(29)
sli
(k-S)-
sh (k
•
6')
=
—2—
=
konst.
Satz 81: Das Produkt der
hyperbolischen Sinus der mit k multiplizierten senkrechten
konjugierter achsenparalleler Durchmesser einer Parabel vom Scheitelpunkt
ist konstant, nämlich gleich dem Quadrat des hyperbolischen Sinus des senkrechten Abstandes der beiden achsenparallelen Asymptoten vom Scheitelpunkt.
Abstände zweier
Die
Bedingung
für die Realität dieser
wie auf Seite 60 für die Parabel mit
Asymptoten
ist:
p
>• 0, oder p
(p
—
1) > 0,
eigentlichem Scheitelpunkt ebenfalls gefunden wurde.
Konjugierte achsenparallele Durchmesser einer, hyperbolischen Parabel liegen
auf
derselben
Seite bezüglich der Achse, konjugierte Durchmesser einer elliptischen
stets
Parabel dagegen liegen auf verschiedener Seite der Achse.
Satz 82:
67
Für die Koordinaten des
jugierten
Punktes
P
zu
bezüglich
des Büschels nomothetischer Parabeln kon¬
Q finden wir:
V
ax,'
a
(30)
Die Koordinaten der
=
=
(1
—
p) y±' ya'
2py3'*.
—
2p
y2' y3',
.
Verbindungslinie PQ sind:
2 pys» + {l-p)ytnya',
a &
2 (1
2 p yt' y3»
a Ç,'
*) 2// y,' yB(,
a Ç„'
2p y2'* y,',
(1
p) y,' y* -2py^ y3'*
nach
und
Weglassung des Faktors y^'3:
y3'
vy1' setzen,
p vyt'
aÇ1'
[(l-j»)|i« + 2p].v«
oÇ,'
2i»ti.v« + 2(l—i>)[i.v»
a V
2p-] v2.
j») (i2
2p |x2 v3 + [(1
=
(31)
=
=
oder,
wir
wenn
yi'
=
-
-
-
-
=
=
(32)
=
=
Das Bestehen dieser 3
Gleichungen
•
-
ist
an
oder
2p p
-2pu.2
Bedingung geknüpft:
Ç/
Ê,'.
-2(l-i0n
(1—i»)|i* —2j», 5.«
(l-p)ii*-\-2p,
(33)
•
-
-
die
0
,
=0,
,
,
,
wenn
a*1'=+2l>n[(l-p)|i1, + 2i>]
a*,'= + [(l-i»)ji« + 2j,]«
2 (1 -p) p [(1 -jp) (x2 + 2p]
a V
(34)
-
die Unterdeterminanten
von
nichts anderes
so
laufen.
bedeuten:
festbleibt, solange Pund Q
Die Werte Zi erfüllen überdies
Gleichung
von
(#/,
v
der nichtabsoluten achsennormalen
:
.(l-p)x1'-px3,
Durch diesen Punkt B
konjugierten
Berührungspunkt
der beiden
dem
die
B
ganz unabhängig
auf zwei konjugierten Durchmessern
Da aber die Koordinaten dieses Punktes
heißt das, daß B
Asymptote
(36)
den
(33)
bedeutet, als daß die Gerade PQ (^', £2', Ç3') durch den Punkt
£2', ^3') hindurchgeht.
sind,
in
VSi' + '.'Ç.' + VÉ^O,
(35)
was
£/, Ç2', ?3'
beiden Durchmesser.
gehen
auch die
Durchmesser mit der
Die
von
Parabel und
Verbindung
=
0
Schnittpunkten T, T'
Parabel,
isotropen Tangenten in
A. K. gegenüberliegenden Endpunkten der
Tangenten t,
t' in den
ebenso die
dieser beiden Enden ist
Punktes B; sie steht daher auf der achsennormalen
die
absolute Polare
senkrecht und
des
durch
Asymptote
geht
Asymptote entsprechenden Asymptotenpunkt. Der Punkt B ist immer uneigentlich,
seine absolute Polare immer eigentlich (siehe Fig. 30).
Satz 83: Die Sehnen einer Parabel, welche durch ein Paar konjugierter Durchmesser
halbiert werden, gehen sämtlich durch einen festen Punkt der achsennormalen Asymptote,
d. h. sie stehen senkrecht auf der gemeinsamen Parallelen der beiden Durchmesser, die
ihrerseits zur Asymptote normal steht, bezw. durch den auf der Parabelachse liegenden
Asymptotenpunkt geht.
den dieser
68
Satz 84: Der
zur
Ort der
geometrische
Asymptote
achsennormalen
punkt
Achse
der
Parabelachse
Der
Büschels
Asymptote
besteht
die auf einer Senkrechten
lotrecht stehen oder eine Gerade durch den
Ort der
geometrische
einer Geraden
zwei Parallelen
konjugierter Durchmesser
Zieht
Sehnen,
Asymptoten¬
schneiden, ist ein Paar konjugierter Durchmesser,
homothetischer
oder
aus
aller
die
zur
parallel gehen.
Satz 85:
eines
senkrecht
Mittelpunkte
Berührungspunkte
der
Parabeln,
die
durch
Asymptotenpunkt
zur
den
auf
Tangenten
Normalen
einer
zur
alle Kurven
an
achsennormalen
der Achse senkrecht
Achse, welche für alle Parabeln
des Büschels
stehen,
ein Paar
darstellen.
sämtlichen Normalen
achsennormalen
Asymptote, bezw. zu allen
liegenden Asymptotenpunkt diejenigen Parallelen zur
Achse, die mit dieser den Berührungspunkt der Parabel mit dem A. K. als Ende gemeinsam
haben, so erhalten wir die Gesamtheit der Paare konjugierter Durchmesser.
man
zu
zur
Geraden durch den auf der Achse
Ebenso wie die
mit
dem
Verbindungslinien
A. K. durch
einen
festen
der
Schnittpunkte
Punkt
zweier
konjugierter
Achse, nämlich den
der
der
Durchmesser
achsennormalen
Asymptote entsprechenden Asymptotenpunkt gehen, so ist dies auch der Fall für die Ver¬
bindungslinien der Schnittpunkte zweier konjugierter Durchmesser mit der Parabel selber.
Satz 86: Die
Verbindungslinien der Schnittpunkte aller Paare konjugierter Durchmesser
gehen durch einen festen Punkt, den nichtabsoluten Leitpunkt
einer Parabel mit derselben
der Achse.
Wir bilden
noch
die
Gleichungen
der
Polaren
r
und r*
von
B
in
Bezug
auf die
Parabel und den A. K.:
2p (1 —p) ^
(37)
r:
(38)
r*:
2
(1 -p) fi<
Eliminieren wir hieraus
#2',
so
-
-
[(1 —p) fi2 + îp]**' + %P (2 -p) H*,'
[(1 -p) ^-f 2p~] z2' + %P H*3'
erhalten wir die
Gleichung
Satz 87: Die
der achsennormalen
Verbindungslinie
der Parabel steht senkrecht auf
auf der
gemeinsamen
Satz 88: Zieht
Gerade,
einen
der
0
0
Gleichung:
(l—p)x1'—px3'
d. h. die
=
=
=
0
Asymptote.
Schnittpunkte zweier konjugierter Durchmesser mit
die im Asymptotenpunkt der Achse
derjenigen Geraden,
Parallelen der beiden Durchmesser senkrecht steht.
man
durch einen festen Punkt einer Geraden zwei zueinander normale
ihnen
diejenigen beiden Parallelen, die zur gegebenen Geraden gleich¬
sinnig parallel sind, zur andern durch einen zweiten gegebenen Punkt der Geraden das
Lot, so ist der geometrische Ort der Schnittpunkte dieses Lotes mit den beiden Parallelen
zur
von
Parabel, welche die gegebene Gerade zur Achse, den ersten Punkt zum Asymptoten¬
punkt, den zweiten zum Leitpunkt und die beiden Parallelen zu konjugierten Durch¬
eine
messern
hat.
Aufgabe
und
die
26 : In einem Punkt einer Parabel die
achsennormale
punkt gegeben
sind.
Asymptote,
bezw. der
Tangente zu zeichnen, wenn die Achse
entsprechende Asymptotenpunkt oder Leit¬
'
69
legen wir den achsenparallelen Durchmesser TF.
Ziehen wir dann durch den. zweiten Endpunkt U desselben eine Gerade UU' senkrecht zur
Asymptote h, bezw. durch den zugehörigen Asymptotenpunkt E* und fallen wir von T
auf UU' das Lot, so ist dies die gesuchte Tangente t.
Wir geben noch die wichtigsten Resultate über konjugierte Achsenpunkte:
Satz 89: Konjugierte Achsenpunkte der eigentlichen Achse liegen harmonisch zum
absoluten und dem nichtabsoluten Brennpunkt der Achse.
Lassen wir den einen der beiden konjugierten Punkte mit dem Scheitelpunkt der
Parabel zusammenfallen, so ist der zugehörige Punkt identisch mit dem Mittelpunkt des
Krümmungskreises im Scheitelpunkt. Für den Krümmungsradius finden wir die Formel:
Lösung: Durch den gegebenen Punkt
T
th(k'p)
=
p.
Satz 90: Die Pole einer Geraden durch einen
im absoluten
Brennpunkt (der isotropen
konfokalen Schar
von
Parabeln
liegen
geht. Die
gegebenen
Achse der
Punkt der
in
Parabel)
Bezug
isotropen Tangente
auf alle Kurven einer
die durch einen zweiten festen
auf einer Geraden,
konjugierten Geraden stehen senkrecht auf
Brennpunkt der Achse aus werden kon¬
Winkel gesehen.
Punkte
der
Achse
rechtem
unter
stets
jugierte
isotropen
Satz 91: Konjugierte Achsenpunkte der isotropen Achse liegen auf gleicher oder un¬
gleicher Seite des absoluten Brennpunktes, je nachdem die beiden dieser Achse angehörigen
Brennpunkte reell oder imaginär sind. Ersteres ist also der Fall für die ein- oder zwei¬
teilige konkave hyperbolische und die uneigentliche konvexe elliptische Parabel, letzteres
für die konvexe hyperbolische und die eigentliche oder uneigentliche konkave elliptische
Punkt
der
isotropen Achse
zwei Parallelen
zur
Achse.
beiden
Vom nichtabsoluten
Parabel.
Satz 92: Die
Parabel
halbiert
Punkte, für
werden
konjugierten Punkten der
Brennpunkt der Achse.
Umgekehrt gilt der
welche die Winkel zwischen den
durch
Tangenten
Punkte
Verbindungslinien
isotropen Achse, liegen auf einer Geraden
die
der
Satz 93: Die Winkelhalbierenden, der Winkel zwischen den
mit
an
gegebene
gegebenen
eine
zwei
durch den nichtabsoluten
Tangenten
von
den Punkten
einer
an
gegebenen Sekante durch den nicht absoluten Brennpunkt der Achse einer Parabel
dieselbe gehen durch zwei feste, konjugierte Punkte der isotropen Achse.
Oder
Satz 94:
gemeinsamen
Tangenten
nichtabsoluten
allen Kurven der Schar
Satz 95."
und Normalen
Ziehen
in den
Schnittpunkten einer
Geraden durch den
der Achse
einer Schar konfokaler
Brennpunkt
gehen durch zwei konjugierte Punkte der isotropen
wir
allen Paaren
konjugierter
Parabeln mit
Achse.
isotropen Achse die
nichtisotropen Tangenten an eine gegebene Parabel, so liegen die Schnittpunkte dieser
Tangentenpaare auf einer Geraden, der Leitlinie des nichtabsoluten Brennpunktes der Achse.
Die Schnittpunkte der Paare von Tangenten aus konjugierten Punkten an den A. K. liegen
auf der zugehörigen Brenngeraden.
von
Punkte der
Wir erwähnen noch den Ortssatz:
Satz 96:
Der
geometrische
Ort
des
Scheitelpunktes
eines
rechten
Winkels,
dessen
70
Schenkel auf zwei Geraden mit
gemeinsamem Ende senkrecht stehen, ist die gemeinschaft¬
gegebenen Geraden.
Um den Grenzübergang zu Euklidischer MaÊbestimmung zu vollziehen, müssen wir in
Gleichung (2) und (3) &a22 durch a22 ersetzen, worauf wir nach Division durch Je zur
Grenze Je
Sonst würde (2) degenerieren in das Paar der Achsen
0 übergehen können.
Unter
und
0
0.
der
gemachten Voraussetzung geht (2) über in die Euklidische
xl
x3
liche Parallele der beiden
=
=
=
Parabel
x22
Aus (3)
dagegen geht
—
2px1x3
=
0.
die absolute Gerade hervor in der Form:
nur noch ein einziger Kurventypus : die eigentliche elliptische Parabel mit
einzigen reellen Brennpunkt auf der Achse ohne eigentliche Asymptote (die achsen¬
normale Asymptote fallt mit der unendlich fernen Geraden zusammen).
Wir bemerken,
daß die Euklidische Parabel sich als Grenzfall zweier verschiedener Kurven der hyperbolischen
Geometrie ergibt.
Es existiert
einem
Das homothetische Büschel
von
x22
besteht
Parabeln der Euklidischen Ebene
—
2jp x1 x3
—
x32
=
0
lauter
kongruenten Parabeln mit gemeinsamer Achse, die alle auseinander
Parallelverschiebung längs der Achse. Die Schar konfokaler Parabeln
hervorgehen
ist nicht spezialisiert, obwohl alle Parabeln untereinander ähnlich sind.
Von allen Paaren konjugierter Durchmesser fällt stets der eine mit der unendlich
fernen Geraden zusammen, so daß die durch die zugehörigen Durchmesser halbierten Sehnen
parallel werden. Die Involution konjugierter Achsenpunkte der eigentlichen Achse besteht
aus Paaren von Punkten, die bezüglich des Brennpunktes symmetrisch liegen.
aus
durch
§
Als
(1)
der oskulierenden Parabel wählen wir
Gleichung
Jcxx
während die
=
X.? -\- Je2
Je* an
Gleichung
iàxx
Hiebei stellt x2
Die
(4)
(5)
K^
=
=
k* x2
0 die
Gleichung
=
#32
an
#32 -\-
=
Je2x2-\-Je2xi2
durch an und setzen wir
(1)
Jcxx
(3)
Die
an
—
2 P a12 x1x2
+ Je2 x*
einzige
reelle
—
—
x32
—
=
an
p,
—
I.
Teil, § 4):
2 Je aVi x2x3
=
=
0
so
0.
geht (1)
x3i-\-2 hp x2 (Je x1 —x3)
Asymptote
über in
=
0
dar.
der oskulierenden Parabel in Linienkoordinaten ist:
(Je2+pi)^+Jen2z-¥Qe2-p'i)^-2Jep^ + 2Jepni^-2Je2p^3^0
Gleichung
des nichtabsoluten
F:
'
Brennpunktes ist:
i»Ç1-2*Çï + Aj»^
_
dessen Koordinaten sind:
(6)
(siehe
des A. K. lautet:
(2)
Dividieren wir
Die oskulierende Parabel.
3.
F(p,-2Je,Jep)
=
0;
71
der Brenn- und
Wir ermitteln die
zur
Gleichungen
Asymptote gleichsinnig parallel
Leitgeraden,
(7)
f:
Jcpx1— 2k2x2—px3
(8)
l:
1c p
Diese
Gleichungen zeigen,
(siehe Fig. 31),
x1-\~
2 Tc2 x2
—
px3
daß Brenn- und
sich auch rein
Asymptote
Leitgeraden.
Satz 97:
Brenn- und
was
Die
die beide
eigentlich
und
sind:
Leitgerade
synthetisch ergibt.
einer
oskulierenden
Der Wortlaut der Sätze über die Parabel
=
0
=
0
Asymptote symmetrisch liegen
zur
Parabel ist die Mittelabstandslinie der
spezialisiert
sich weiter für die oskulierende
Parabel :
Satz 98:
Parallele
Endpunkt
zur
Zieht
man
Asymptote
durch
nach
einen
dem
dieser Parallelen das Lot
beliebigen
Punkt
Oskulationspunkt
zur
Tangente
im
einer oskulierenden Parabel die
und
fällt
man
durch
gegebenen Punkt,
so
den
andern
steht dasselbe
72
auch senkrecht auf der
Brenngerade
dem
und
Asymptote und hat mit
Spiegelbild der Parallelen
dem Lot
in
vom
Bezug
auf
gegebenen Punkt auf die
die Asymptote ein Ende
gemeinsam.
Hieraus
folgt
die
27:
Die
Lösung der
Aufgabe
Tangente in einem Punkt einer oskulierenden Parabel zu zeichnen,
die
wenn
Asymptote oder die Brenngerade gegeben sind.
Lösung : Wir spiegeln die durch den gegebenen Punkt T nach dem absoluten Brenn¬
punkt F' gezogene Parallele zur Asymptote oder Brenngeraden an der Asymptote und
bestimmen die zweite Parallele zum Spiegelbild F'V durch den Punkt T.
Die Winkel¬
halbierende des Winkels zwischen der Verlängerung TU des »Durchmessers" TF' und der
Parallelen TV ist die gesuchte Tangente t.
Es folgt hieraus noch, daß die Normale des
Punktes T senkrecht steht auf dem spiegelbildlichen Durchmesser VF' zu demjenigen durch
den gegebenen Punkt T.
Ist die Brenngerade gegeben, so fällen wir vom Punkte T das Lot auf die Brenn¬
gerade f* und halbieren die von diesem Lot und dem Durchmesser TF' gebildeten Winkel.
Es ergeben sich in diesem Falle zwei Lösungen, da jeder Punkt auf zwei Kurven einer
Schar konfokaler oskulierender Parabeln liegt.
Aufgabe 28: Eine oskulierende Parabel ist gegeben durch die Asymptote oder Brenn¬
gerade und eine Tangente. Es soll der Berührungspunkt konstruiert werden.
Lösung: Ermitteln wir das gemeinschaftliche Lot von Tangente und Asymptote, so
treffen die beiden zu diesem Lot parallelen Durchmesser F' ü und F' V die Tangente t in
denjenigen beiden Punkten, in welchen die Tangente von je einer oskulierenden Parabel
eines homothetischen Büschels berührt wird.
Spiegeln wir den Oskulationspunkt der Kurve, also den einen Endpunkt der gegebenen
Brenngeraden an der gegebenen Tangente t und fällen wir vom Spiegelpunkt V das Lot
auf die Brenngerade f*, so begegnet dasselbe der Tangente t in ihrem Berührungspunkt
mit der Kurve.
Wir könnten auch die Brenngerade f* an der gegebenen Tangente t
spiegeln; der zum Spiegelbild normale Durchmesser trifft die Tangente wiederum im ge¬
suchten Berührungspunkt.
Aufgabe 29: Gegeben ist ein Punkt einer oskulierenden Parabel samt Tangente und
die Richtung nach dem Oskulationspunkt. Man konstruiere die Asymptote und die Brenn¬
gerade.
Lösung: Wir ermitteln den Durchmesser des gegebenen Punktes und fällen von dem¬
jenigen Endpunkt desselben, der dem Oskulationspunkt gegenüber liegt, das Lot auf die
gegebene Tangente t. Die Mittelabstandslinie der beiden zu diesem Lot UV parallelen
Durchmesser F' U, F' V ist die Asymptote der oskulierenden Parabel.
Ziehen wir durch
den Punkt T die zweite Parallele TV
den
zu
Punkte
erwähnten Lot
UV und bestimmen wir wieder
Durchmesser, so ist dies die Brenngerade.
die oskulierende Parabel, so umhüllt das Spiegelbild der Brenn¬
Umhüllt die
geraden
zum
dieser Geraden normalen
in
Tangente t
Bezug auf die Tangente
Oskulationspunkt F'.
Fußpunkte der Lote von den
Spiegelpunkte
Parabeltangenten auf die Brenngerade.
dieses Grenzkreises
rührungspunkten
der
sind
die
einen Grenzkreis
um
der
den
Die
Be¬
73
Satz 99 :
Spiegelt
die
Brenngerade einer oskulierenden Parabel an allen Tangenten
Spiegelbilder einen Grenzkreis um den Oskulationspunkt. Dieser
Grenzkreis trifft die Brenngerade in ihrem Schnittpunkt mit der Parabel und zwar halbiert
die Parabeltangente dieses Punktes den von der Grenzkreistangente und der Brenngeraden
eingeschlossenen rechten Winkel.
Satz 100: Die Tangenten in den Schnittpunkten eines beliebigen Durchmessers mit
der oskulierenden Parabel und dem Grenzkreis treffen sich auf der Brenngeraden derart, daß
die Parabeltangente den von der Grenzkreistangente und der Brenngeraden gebildeten Winkel
derselben,
so
man
umhüllen die
halbiert.
Satz 101: Die oskulierende Parabel ist der
geometrische Ort aller Punkte,
gleichen Abstand haben.
Grenzkreis und einem seiner Durchmesser
Um die
Beziehung konjugierter
wieder die Transformation
Durchmesser abzuleiten, wenden wir auf die
(7)
ksÇi-\-xB
V
daß die
Gleichung
few
während der A. K. wieder
=
x*
einem
Gleichung (3)
h x2
+
2
=
=
=
ax1'
oxa'
x2
a
Parabel,
x,' x3' +
^2p=p'
wenn
2
p' xj x3'
=
gesetzt wird, lautet:
0,
ist durch
gegeben
(9)
Wx.x.=xi'i-\-2x1'x3'^0.
Nach
eines
dem
beliebigen
bereits
bekannten
Punktes P
(10)
hc,
(11)
wxy
Der
2
der oskulierenden
(8)
von
an:
kxl—x3
so
die
Schnittpunkt Q
=
=
(yt,
yït
Gedankengang bilden wir die Gleichungen der
y3 bezw. yt', y^', y3) in Bezug auf & und o>:
y3' V + (y2' +P1 y3') x,' -f {yt* + p' yj) x3'
0
y3'x1'-{-y2'x2' + 2/1'a;3'
«/
a^'
a^3'
a
Zwischen den Koordinaten des
0
=
der Polaren p und
(12)
=
Polaren
besitzt die Koordinaten:
p*
=
=
=
y3'
ftV
y3n
Vi
—
y2'2
—
gegebenen
Punktes P und
auf das Büschel nomothetischer oskulierender Parabeln
denjenigen des zu P in Bezug
konjugierten Punktes Q besteht die
Beziehung:
^v=-
(i3)
d. h.
der
wenn
-K,
der eine der beiden Punkte
konjugierte
Punkt einen zweiten
P, Q einen Durchmesser durchläuft, so beschreibt
Durchmesser, den wir als den zum ersten konjugierten
Durchmesser bezeichnen.
Satz 102:
Gleichung (13) enthält den
Konjugierte Durchmesser einer oskulierenden
Parabel
liegen
zur
Asymptote
symmetrisch.
Die
(14)
Gleichung
Verbindungsgeraden PQ lautet:
2 ya> y* < + *,/ (y," -2y> y3>) xt'
der
-
y« x3'
=
0
10
74
Für den
Schnittpunkt
2y3'*x1'-y2'*x3'
(15)
die
zeigt,
Sehnen einer oskulierenden Parabel,
somit
einen
durch
und
denselben
Gleichung:
0,
=
x2' : x3 konstant ist. Die
die durch einen Durchmesser halbiert werden, gehen
bleibt, solange
daß R unveränderlich
sich die
Asymptote .ergibt
R mit der
das Verhältnis
der Asymptote, der sich leicht, geometrisch
gemeinsamen Parallelen des gegebenen und seines
gibt.
Punkt R
oder rechnerisch als der absolute Pol der
konjugierten
Durchmessers
Satz 103:
messer
und
Parabel, die
Alle Sehnen einer oskulierenden
halbiert werden,
des
erkennen
zu
von einem gegebenen Durch¬
gemeinsamen Parallelen des gegebenen
Lot zur Asymptote, das zum gegebenen
senkrecht auf der
stehen
konjugierten Durchmessers (oder dem
parallel ist).
in der Beziehung (15) der Parameter p' nicht vorkommt, bedeutet,
Durchmesser
Daß
unverändert
bleibt,
die Kurve h durch
wenn
daß der Punkt R
eine andere des durch h bestimmten
nomo¬
thetischen Büschels ersetzt wird.
Sind
Kçç
(16)
h=
p* ^ +CS«
-
2 j»
^ Ç,4 +
2
Çt« Ç8«
'
0
=
und
(17)
(
2T6Y
(18)
=
Çï<l + 2Ç1'Ç,'
=
0
(p'* V -p' V + ,,') Si' + (V -p' V) Ça' + V Es'
=
o
Q^zzr^' + ^' + V^O
(19)
die
=
der oskulierenden Parabel und des A. K. in Linienkoordinaten, also
Gleichungen
die
%e
Gleichungen
gegebenen Geraden p (rj/, rj„', rj3') in Bezug auf die
so
ergeben sich für die Koordinaten der Ver¬
der Pole P, P* einer
oskulierende Parabel Je und den A. K. w,
bindung
q
von
P und P* die "Werte:
St'= -?'*"
a£2'
-yv(i>v-v)
a
(20)
=
Daraus entnehmen wir die
Beziehung:
¥r + ^,
(21)
Durch
die Verhältnisse der Linienkoordinaten
=
p'
i]./:^'
?2': jj/
und
sind auf der
isotropen
Achse, d. h. also der isotropen Tangente des Oskulationspunktes zwei »konjugierte Achsen¬
X, £2' : £/ —p'
X, so finden wir als Koordinaten
punkte" bestimmt. Setzen wir tj2' : rjt'
=
zweier
konjugierter
Punkte die
—
Wertetripel:
(22)
ox1'=
(23)
ax1'
=
—
0X^
X,
~p'-{-X,
Die Polaren dieser beiden Punkte sind
=
1,
oa;2'
gegeben
a£3'
=
l,
x,'
(25)
«î, + (-J', + X)*s,
XxB'
=
=
0
Gleichungen:
0
=
0
a«3'
durch die
(24)
—
=
0
75
Bilden wir nach der in der
Anmerkung
Winkelhalbierenden, bezw. Mittelabstandslinie,
2x2'
(26)
welche die
Brenngerade
—
so
p'x3'
=
eine
Tangenten
von
einem
beliebigen Punkt
bezüglich der
sind.
Tangente und Normale in einem beliebigen Punkt einer oskulierenden Parabel
bezüglich der Brenngeraden symmetrischen Durchmessern senkrecht.
Euklidischer Maßbestimmung zerfällt die oskulierende Parabel in die doppelt
Satz 105:
stehen auf zwei
gezählte
0,
oskulierende Parabel stehen senkrecht auf zwei Durchmessern, die
Brenngeraden symmetrisch
Bei
der
darstellt.
Satz 104: Die Winkelhalbierenden der beiden
an
angegebenen Weise die Gleichung
resultiert die Gleichung
auf Seite 17
unendlich ferne Gerade.
Berichtigung.
Auf Seite
5, Zeile 5,
muß es heißen
:
p
•
if
=
k
Auf Seite
16, Zeile
12 bis 18 und Seite
h
Ji
=
2 aik xk,
1, 2, 3
17, Zeile
1 und
2, muß
'
*
'*
TJ
TT
es
heißen:
Inhalt.
Seite
Einleitung
I. Teil.
II. Teil.
in. Teil.
1
Allgemeines über Kegelschnitte der hyperbolischen Geometrie:
§ 1. Definitionen und Hauptsätze der hyperbolischen Geometrie
§ 2. Zusammenhang mit der Theorie der Polarsysteme
§ 3. Mittelpunkte, Achsen, Asymptoten und Brennpunkte der Kegelschnitte
§ 4. Einteilung der Kegelschnitte
§ 5. Gemeinsame Definition und einige allgemeine Sätze über Kegelschnitte
3
5
...
5
G
.
.
11
Sätze und Konstruktionen für
allgemeine Kegelschnitte:
Kegelschnittbüschel
§
1.
Das nomothetische
§
2.
Das Dreieck konstanten Inhalts
18
§
§
§
§
§
§
§
§
3.
Die konstante
20
4.
5.
6.
7.
8.
9.
10.
Asymptotenstrecke
Die Schar konfokaler Kegelschnitte
Der konstante Winkel am Brennpunkt
Beziehungen zwischen Asymptoten und Brennpunkten
Konjugierte Durchmesser
Konjugierte Achsenpunkte
Konstruktionen von Asymptoten und Brennpunkten
Die Semihyperbel
12
23
28
31
36
41
45
49
Sätze und Konstruktionen für
§
§
§
spezielle Kegelschnitte:
parabolische Hyperbel
1.
Die
2.
Die Parabel
3.
Die oskulierende Parabel
52
60
70
.
<
Leer
-
Vide
-
Empty
Lebenslauf.
Ich
wurde
am
26. März 1894
geboren in Tuttwil (Kt. Thurgau), als Sohn des Emil
Emma, geb. Sprenger, Bürger von Eschlikon und Braunau
Leutenegger, Lehrer,
(Kt. Thurgau). Ich besuchte in Erlen die Primär- und Sekundärschule und trat im Frühling
1909 in die Industrieabteilung der Thurgauischen Kantonsschule in Frauenfeld ein, wo ich
im Herbst 1912 die Maturitätsprüfung bestand.
Mit der Sekundarlehramtsprüfung als Ziel, studierte ich je ein Semester an den
Universitäten Zürich und Neuchâtel, um aber schon im Herbst 1913, meiner Neigung
folgend, an die Abteilung der Fachlehrer für Mathematik und Physik der Eidgenössischen
Technischen Hochschule überzutreten. Im Juli 1917 bestand ich die Diplomprüfung.
und der
Nachdem ich bereits im Herbst 1916 als Stellvertreter
geamtet hatte,
schule
war
ich
St. Gallen und
vom
an
Herbst 1917
bis
zum
Zürich.
der Industrieschule
Wintersemesters 1917/18 durfte ich
zugleich
Frühling
an
der Kantonsschule Aarau
1918 Vikar
an
der Kantons¬
Während der zweiten Hälfte
des
Herrn Prof. Dr. M. Großmann in Darstellender
Geometrie assistieren.
Im
wo
Frühjahr
1918
erfolgte
meine Wahl
ich seither als Lehrer für Mathematik
Es ist mir
auszusprechen
Abfassung
eine
angenehme Pflicht,
für all seine
Ratschläge,
die
an
an
die
Thurgauische Kantonsschule Frauenfeld,
den oberen Klassen wirke.
Herrn Prof. M. Großmann meinen
er
besten Dank
mir während meiner Studienzeit und bei der
dieser Arbeit hat zuteil werden lassen.
Emil
Leutenegger,