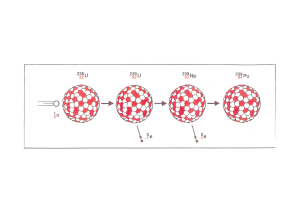
03_Naturwissenschaftliche Grundlagen_18_09_11
Werbung

Kapitel 3 Naturwissenschaftliche Grundlagen Abbildung 3-1 Atomzeichen - einmal anders.. NATURWISSENSCHAFTLIC NATURWISSENSCHAFTLICHE GRUNDLAGEN 2 Einleitung 2 Grundlagen der Atomphysik Elemente Das RUTHERFORD-Experiment Experiment Atomaufbau Anti-Materie Kernspaltung 2 2 3 3 11 13 Grundlagen der Strahlenphysik Ionisierende Strahlung Der radioaktive Zerfall Strahlungsarten 14 14 14 21 Wechselwirkung von Strahlung mit Materie Energieübertragung und Strahlenwirkung Wechselwirkungen von α - Strahlung Wechselwirkungen von β - Strahlung Wechselwirkungen von γ - und Röntgenstrahlung Wechselwirkungen von Neutronen 27 27 33 33 35 40 Strahlendosen, Dosisgrößen und Dosiswirkungsbeziehungen Dosiswirkung Energiedosis D (absorbed dose) Ionendosis I Strahlenschutzgrössen (Körperdosisgrössen) Operationelle Größenn (Meßgrößen) Erweiterte Dosisbegriffe nach ICRU und ICRP Dosiswirkungsbeziehungen 41 42 42 42 45 45 48 Dosisleistung und Geometrieeinflüsse Dosisleistung bei punktförmige Strahlenquellen: Dosisleistung bei kreisscheibenförmigen Strahlenquellen: 49 49 50 Strahlung im Alltag 50 Beispiele für Radionuklidanwendungen in der Nuklearmedizin 52 Übungsfragen 53 Literatur: 53 Dazu im Internet 53 Seite 3-1 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Naturwissenschaftliche Grundlagen ...Manchmal musste ich einen ganzen Tag lang eine siedende Masse mit einer Eisenstange umrühren, die fast ebenso groß war wie ich. Abends war ich zum Umfallen müde...in das Laboratorium kamen nur sehr wenige Leute: der eine oder der andere Physiker oder Chemiker besuchte uns von Zeit zu Zeit, entweder um unsere Experimente zu sehen, oder um Pierre Curie...um einen Rat zu bitten. Dann gab es vor der schwarzen Tafel jene Gespräche, an die man so gerne zurückdenkt, weil sie auf das wissenschaftliche Interesse und die Arbeitsintensität stimulierend wirken... Marie Curie um 1900 Einleitung Die Atomphysik handelt vom Aufbau der Materie und vom Umwandeln der Masse in Energie, bzw. umgekehrt. In der Strahlenphysik werden die Gesetze des radioaktiven Zerfalls behandelt, sowie die Wechselwirkungen von Strahlung mit der Materie, welche die wichtigste Grundlage für das Verständnis der Technik von Strahlenmessungen ist. Diese Wechselwirkungsprozesse sind auch Ursache biologischer Strahlenschäden. Die Lehre von Wirkung und Anwendung ionisierender Strahlen auf Substanzen (im "Reagenzglas") dagegen wird als Strahlenchemie bezeichnet. Unter Radiologie verstehen Naturwissenschaftler ganz allgemein die Lehre von den ionisierenden Strahlungen und ihren Anwendungen in Medizin und Biologie. Häufig wird Radiologie in der Medizin mit Strahlenheilkunde gleichgesetzt, also den Anwendungen ionisierender Strahlung in Diagnostik und Therapie. Grundlagen der Atomphysik Elemente Die stoffliche Welt um uns herum lässt sich zerlegen in kleine - einst als unteilbar geglaubte - Teilchen, die als Atome bezeichnet werden. Bis heute sind ca. 114 verschiedenen Atomsorten bekannt. UNTER EINEM CHEMISCHEN ELEMENT VERSTEHT MAN EINEN CHEN CHEMISCHEN EIGENSCHAFTEN AUFGEBAUT IST. Seite 3-2 STOFF, DER AUS ATOMEN MIT GLEI- Kapitel 3 Naturwissenschaftliche Grundlagen Das RUTHERFORD-Experiment Grundlegende Erkenntnisse zum Aufbau der Materie fand RUTHERFORD durch seine Streuexperimente heraus. Er beschoss eine dünne Goldfolie mit 2-fach positiv geladenen He-Kernen (sog. αStrahlung). Viele der He-Kerne gelangten durch die Folie nahezu ungehindert hindurch, andere wurden in Winkeln von > 90° zur Ausbreitungsrichtung gestreut. Diese Ergebnisse ließen sich nur durch die Annahme erklären, dass die Materie eigentlich aus "Nichts" mit einigen wenigen kleinen Streuzentren besteht, wobei diese Streuzentren eine positive Ladung tragen mussten, sonst wäre eine derartige Rückstreuung nicht möglich. Atomaufbau Atomkern Atome bestehen aus einem positiv geladenen Atomkern (dem RUTHERFORDschen Streuzentrum) und einer darum befindlichen negativ geladenen Hülle. Dabei beträgt der Durchmesser des Atoms ca. 10-10 m. Fast die gesamte Masse des Atoms ist in seinem Kern vereinigt, der einen Durchmesser von ca. 10-15 m aufweist. Materie besteht demnach also aus Massezentren, die relativ weit voneinander entfernt sind. Der Atomkern - so stellte es sich bei genaueren Untersuchungen heraus - besteht aus einzelnen positiv geladenen Bausteinen, den Protonen (je eine positive Elementarladung) und einzelnen elektrisch neutralen Bausteinen, den Neutronen. Protonen und Neutronen besitzen beide annähernd die gleiche Masse (Differenz ca. 1 / 2000tel), sie werden zusammen auch als Nukleonen (Kernbausteine) bezeichnet. Protonen bzw. Neutronen gehören zu den Elementarteilchen aus denen Materie aufgebaut ist. Es herrschen zwischen den Protonen im Kern elektrostatisch abstoßende Kräfte. Diese werden jedoch durch noch stärkere Wechselwirkungen mit Neutronen kompensiert (Kernkräfte). Ein stabiler Kern verfügt deshalb stets über ein bestimmtes Zahlenverhältnis von Protonen zu Neutronen. Stimmt dieses Zahlenverhältnis nicht, so wird der Kern instabil und das betreffende Atom zerfällt nach einer gewissen Zeit, was als Phänomen der Radioaktivität beobachtet wird. Wegen der vielen positiven Ladungen sind Atome, die mehr als 92 Protonen besitzen, immer radioaktiv. Durch Kombination verschiedener Anzahlen von Neutronen und Protonen erhält man verschiedene Kernarten, die auch als Nuklide bezeichnet werden. DIE SUMME DER PROTONEN EINES NUKLIDS WIRD ALS SEINE ORDNUNGSZAHL BEZEICHNET, SUMME VON PROTONEN UND NEUTRONEN EINES NUKLIDS WIRD ALS SEINE MASSENZAHL ZEICHNET. Seite 3-3 DIE BE- S. Prys / E. Foßhag Fachkunde im Strahlenschutz Man findet, dass die Atomkerne der leichteren Elemente dann stabil sind, wenn die Anzahl von Protonen und Neutronen etwa gleich ist. Bei den schwereren Elementen ist dagegen ein immer größerer Neutronenüberschuss zur Stabilität erforderlich. Untersucht man bei stabilen Nukliden das Verhältnis der Protonen zur Neutronenzahl, dann findet man sehr häufig sowohl geradzahlige Protonenzahlen als auch geradzahlige Neutronenzahlen. Neben weiteren Stabilitätsregeln lassen sich auch "magische Zahlen" an Protonen bzw. Neutronen auffinden, die besonders häufig mit stabilen Kernen einhergehen: 2, 8, 20, 28, 50, 82, 126. Die große Häufigkeit des Auftretens dieser Zahlen bei stabilen Atomkernen wird durch einen schalenförmigen Aufbau der Atomkerne (ähnlich der Elektronenhülle) zu erklären versucht. Abbildung 3-2 Anfang einer Nuklidkarte Eine ausführliche Übersicht über alle Nuklide, sowie deren Eigenschaften bietet die (Karlsruher) Nuklidkarte. Dort werden als Ordinate die Protonenzahl und als Abszisse die Neutronenzahl aufgetragen. Zurzeit sind ca. um die 2500 Nuklide bekannt, die sich auf 112 verschiedene chemische Elemente verteilen. Es gibt 274 stabile Nuklide und 66 natürlich vorkommende radioaktive (z.T. sehr langlebige) Nuklide, welche auch als Radionuklide bezeichnet werden. Von den letzteren treten 46 in den Zerfallsreihen des Urans und des Thoriums auf, z.B. das Nuklid U-235 (p = 92, n = 143), das als spaltbarer Kernbrennstoff Verwendung findet oder das Nuklid U-238 (p = 92, n = 146), das zu 98% in sogenanntem Natururan auftritt. Alle anderen der 2500 Nuklide zerfallen spontan. Seite 3-4 Kapitel 3 Naturwissenschaftliche Grundlagen Abbildung 3-3 Größerer Ausschnitt der Nuklidkarte mit Legende Abbildung 3-4 Gesamte Nuklidkarte Seite 3-5 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Andere (künstliche) Radionuklide wurden nach dem Reaktorunfall von Tschernobyl in manchen Nahrungsmitteln nachgewiesen: I-131 oder Cs-137. Durch Kernspaltung im Reaktor erzeugte Radionuklide bzw. deren radioaktive Töchter wie z.B. Tc-99m werden bei szintigraphischen Schilddrüsenuntersuchungen durch Einspritzen (als wässrige Salzlösung) in den menschlichen Körper und anschließende Aktivitätsbestimmung in der Schilddrüse angewendet. Tc-99m Tc-99 + γ Man kann jeweils bestimmte Nuklide zu Gruppen zusammenfassen: ISOTOPE NUKLIDE WEISEN DIE GLEICHE CHEMISCHEN ELEMENT. ORDNUNGSZAHL AUF UND GEHÖREN DAMIT ZUM SELBEN Isotope stehen in der Nuklidkarte in waagerechten Reihen nebeneinander, haben die gleichen Protonenzahlen, jedoch unterschiedliche Neutronenzahlen, gleiche Elektronenkonfiguration und damit die gleichen chemischen Eigenschaften, gehören damit also zum gleichen chemischen Element. Das in der Chemie häufig verwandte Periodensystem der Elemente unterscheidet deshalb nicht zwischen den einzelnen Isotopen eines Elementes. Anders verhält es sich bei den physikalischen Eigenschaften: hier unterscheidet sich Wasserstoff H-1 am stärksten von seinen Isotopen, da diese eine Massezunahme um 100 bzw. 200 % aufweisen. Abbildung 3-5 Wasserstoffisotope Von besonderer Bedeutung sind auch die Isotope des Kohlenstoffes (p = 6) mit den Massen 12, 13, und 14, d.h. n = 6,7, bzw. 8. Von allen Kohlenstoff-Atomen auf der Erde haben 98,9 % die Massen- Seite 3-6 Kapitel 3 Naturwissenschaftliche Grundlagen zahl 12, 1,1 % die Massenzahl 13 und nur in Spuren kommt das radioaktive C-14 vor. Es entsteht dadurch, dass Neutronenstrahlung in die Atmosphäre eintrifft, dort auf Stickstoffatome fällt. Durch eine anschließende Kernreaktion entsteht aus N-14 das Spurenelement C-14. Es handelt sich um einen β-Strahler (radioaktiver Zerfall unter Aussendung von Elektronenstrahlen) mit einer Halbwertszeit von 5730 Jahren. Als radioaktives Kohlendioxid gelangt es über die Photosynthese in die Pflanzen und Biomasse. Das Zahlenverhältnis von C-14 zu stabilem C-13 beträgt stets ca. 1: 1012. Aus diesem Verhältnis und der Halbwertszeit von C-14 ergeben sich bei einem lebenden Organismus pro Gramm Kohlenstoff 15,3 Zerfälle pro Minute. Wenn das Lebewesen gestorben ist, sinkt der C-14 - Anteil. Über die restliche Aktivität lässt sich dann das Alter bestimmen (Radiokarbonmethode). C-14 lässt sich auch als sog. Tracer (Markierungsstoff) in biologischen Materialien verwenden. Bei kerntechnischen Experimenten hat es die Erzeugung und Freisetzung von "künstlichem" C-14 durch Kernwaffentests gegeben. ISOBARE NUKLIDE HABEN GLEICHE NUKLEONENZAHLEN, JEDOCH UNTERSCHIEDLICHE KERNLADUNGSZAHLEN. SIE FINDEN SICH IN DEN DIAGONALREIHEN DER NUKLIDKARTE, Z.B. F-17, O-17, N17 ISOTONE NUKLIDE SIND NUKLIDE MIT GLEICHER TEN REIHEN DER NUKLIDKARTE. NEUTRONENZAHL. SIE STEHEN IN DEN SENKRECH- ISOMERE NUKLIDE HABEN ZWAR GLEICHE ANZAHL VON PROTONEN ABER IM ATOMKERN UNTERSCHIEDLICHE ENERGIEGEHALTE. UND NEUTRONEN, BESITZEN Ein instabiler Kern kann entweder durch Kernumwandlung und Aussenden von Kernbausteinen oder durch Abstrahlen seiner überschüssigen Energie in den Grundzustand übergehen. Ein Atomkern, der sich auf letztere Art stabilisiert, erzeugt dabei einen isomeren Tochterkern. Bei isomeren Nukliden handelt es sich quasi um verschiedene Energiezustände desselben Nuklids. Der metastabi- Seite 3-7 S. Prys / E. Foßhag Fachkunde im Strahlenschutz le (angeregte) Zustand eines Kerns wird durch den Index m hinter der Massenzahl gekennzeichnet. Es sind etwa 400 Fälle der Kernisomerie bekannt. Abbildung 3-6 Beispiel: Kernenergieschema für Tc-99m Weitere Untersuchungen ergaben, dass die Kernbausteine (Nukleonen) auch magnetische Eigenschaften besitzen. Wobei Neutronen von einem 3- fach stärkeren Magnetfeld umgeben sind als Protonen und Elektronen. Um die Struktur der Kernbausteine zu ergründen, führte man dem RUTHERFORD-Experiment ähnliche Versuche durch: es wurden Protonen bzw. Neutronen mit Elektronen, deren Energien im GeV-Bereich lagen, beschossen. Auf diese Weise konnte festgestellt werden, dass sich im Innersten der Kernbausteine Objekte mit drittelzahligen Ladungen befinden. Diese Objekte wurden als Quarks (Kunstwort) bezeichnet. Die Quarks bewegen sich im Inneren eines Protons (oder Neutrons) mit hoher Geschwindigkeit. Sie sind punktförmig und besitzen unterschiedliche Massen. Sie lassen sich nicht isolieren. Elektronenhülle Die Hülle des Atoms besteht aus kleineren, negativ geladenen Elementarteilchen, den Elektronen, deren Ladung der negativen Elementarladung e entspricht. Die Anzahl der Elektronen pro Atom entspricht beim neutralen Atom der Zahl der im Kern befindlichen Protonen (Prinzip der elektrischen Neutralität). Elektronen bewegen sich wie Planeten in unterschiedlichen Bahnen (Schalen) um den Kern. Der Zusammenhalt zwischen Atomkern und Elektronenhülle wird durch elektrostatische Anziehungskräfte (sog. schwache Wechselwirkungen, COULOMB-Kräfte) verursacht. Die "Bewegung" der Elektronen verhindert, dass sie in den Kern stürzen und somit das Atom instabil wäre. Eine stabile Elektronenbahn ergibt sich nach dem BOHRschen Atommodell bei einem Kräftegleichgewicht zwischen den elektrostatischen Anziehungskräften und der Zentrifugalkraft. Die Elektronenschalen, werden von innen nach außen durchnummerieret (siehe Abbildung 2-7). Für die Energie E eines Elektrons in Abhängigkeit von Kernladung Z und Bahnradius r gilt: Seite 3-8 Kapitel 3 Naturwissenschaftliche Grundlagen 1 Z ⋅ e2 E=− ⋅ 2 r E e = Energie eines BOHRschen Elektrons = Elementarladung Das Schalenmodell der Atomhülle: Abbildung 3-7 Z = Kernladungszahl r = Abstand zum Kern 2n2 Elektronen pro Hauptschale Elektronenbahnen des BOHRschen Atommodells Ein bewegtes Elektron zeigt je nach Versuchsbedingungen entweder den Charakter einer Welle oder den Charakter eines Teilchens (Korpuskel). Seine Wellennatur zeigt sich darin, dass "Elektronenwellen" interferieren können oder auch Beugungsphänomene aufweisen. Aus Beugungsexperimenten konnte ermittelt werden, dass Elektronen von 50 000 eV eine Wellenlänge von ca. 6.10-12 m aufweisen. Der Teilchencharakter dagegen wird erkennbar, wenn gerichtete Elektronenbewegungen als Stromfluss gemessen werden können. Ein solcher Welle-Teilchen-Dualismus findet sich auch beim Licht, das sowohl als Lichtwelle oder als Lichtteilchen (Photon) beschrieben werden kann. Beim photoelektrischen Effekt kann man beobachten, dass Photonen Elektronen aus einer metallischen Oberfläche herausschlagen können. Dieser Welle-Teilchen-Dualismus, der von DEBROGLIE erstmalig postuliert wurde, bedingt die Tatsache, dass es physikalisch nicht möglich ist beide Erscheinungsformen des Elektrons gleichzeitig mit Meßmethoden zu erfassen. Je genauer man versucht die Wellenlänge eines Elektrons zu ermitteln, desto ungenauer wird die Ortsbestimmung. Dieser Sachverhalt wird auch in der sog. HEISENBERGschen Unschärferelation deutlich. Diese besagt, dass die gleichzeitige Erfassung von Ort und Impuls bei einem Elektron nur mit einer Unschärfe beider Messgrößen möglich ist. Das Produkt dieser Unschärfen liegt in der Größenordnung des PLANCKschen Wirkungsquantums h. Seite 3-9 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Abbildung 3-8 Der Aufbau der Materie Elementarteilchen Elementarteilchen bilden Materie und Anti-Materie, nur manche von ihnen existieren auf der Erde, andere existieren im interstellaren Raum oder auf anderen Planeten. Die Elementarteilchen werden wie folgt eingeteilt: Leptonen: (leichte Teilchen) zusammen mit den Quarks bilden sie Grundbausteine von Materie und Anti-Materie, hierzu gehören u.a. Elektronen und Neutrinos; Mesonen: Elementarteilchen aus Quarkdubletts; Baryonen : (schwere Teilchen) Elementarteilchen aus Quarktripletts, hierzu gehören die Nukleonen (Protonen, Neutronen) und die Hyperonen, unter letzteren versteht man alle Elementarteilchen, die schwerer sind als ein Proton; Eichbosonen: Austauschteilchen, übertragen Kräfte. Nach dem Standardmodell gibt es zwölf Materieteilchen, bestehend aus einer Gruppe, die sechs verschiedene Quarks beinhaltet und einer weiteren Gruppe, die aus sechs verschiedenen Leptonen gebildet wird. Eine dritte Gruppe besteht aus Eichbosonen, sog. Kraftteilchen, welche die Materie zusammenhalten, indem sie elektromagnetische, starke und schwache Wechselwirkungen zwischen den Bausteinen der Materie vermitteln. Seite 3-10 Kapitel 3 Naturwissenschaftliche Grundlagen Quarks Quarks sind Bestandteile von Elementarteilchen, die jedoch isoliert nicht bestehen können. Es gibt insgesamt sechs verschiedene Quarks: up (u), down (d) Protonen und Neutronen, die Grundbausteine unserer Materie, sind aus uund d-Quarks zusammengesetzt, welche die Familie der beiden leichtesten Quarks bilden; strange (s), charm (c) s- und c-Quarks bilden eine zweite Familie, sie ähneln in Ihren Eigenschaften den u- bzw. d-Quarks, sind jedoch schwerer; bottom (b), top (t) b- und t-Quarks bilden die dritte Familie, die aus besonders schweren Quarks besteht, die in Sekundenbruchteilen zerfallen. Die Quarks besitzen nur ein bzw. zwei Drittel der elektrischen Elementarladung. Im Proton ergibt die Summe der Ladungen der drei Quarks gerade die Elementarladung, ebenso beim Neutron. Auch die Magnetfeldstärke der Kernbausteine lässt sich auf die Feldstärken seiner Quarkbestandteile zurückführen. Die Quarks in den Kernbausteinen lassen sich nicht von seinen Partnern abtrennen. Sie werden durch den Austausch von speziellen Kraftteilchen, den Gluonen (englisch "glue" = Klebstoff), zusammengehalten. Anti-Materie Unter Anti-Materie versteht man Materie, die ausschließlich aus Anti-Teilchen besteht. Der Atomkern besteht dabei aus Anti-Protonen (negativ geladene Protonen) und Anti-Neutronen (aus entsprechenden Anti-Quarks) und wird umgeben von den Anti-Elektronen (positiv geladenen Elektronen), auch Positronen genannt. In Laborversuchen konnten bereits Anti-Wasserstoff, AntiDeuterium, Anti-Tritium und Anti-Helium erzeugt werden. Nur das Photon ist mit seinem AntiTeilchen identisch. Anti-Materie ist zusammen mit Materie nicht stabil. Sie wird unter Bildung von Photonen oder Mesonen vernichtet. Nur im freien Raum des Universums, fern von Materie kann Anti-Materie existieren. Gegenstand wissenschaftlicher Untersuchungen ist die Frage, ob andere galaktische Systeme aus Anti-Materie bestehen. Beim Zusammentreffen von Anti-Materie mit "normaler" Materie wandeln sich die Massen der beteiligten Teilchen entsprechend der EINSTEINschen Gleichung E = m ⋅ c2 E = Energieäquivalent eines Teilchens m = Masse des Teilchens c = Lichtgeschwindigkeit vollständig in Vernichtungsstrahlung um. Trifft z.B. ein Elektron auf ein Positron, so entstehen zwei γ-Quanten mit jeweils Energien von 511 keV. Seite 3-11 S. Prys / E. Foßhag Name Fachkunde im Strahlenschutz Symbol Ruhemasse [MeV] Ladung Quarkaufbau ELEMENTARTEILCHENBAUSTEINE: up down strange charm bottom (beauty) top (truth) u d s c b u* d s c b t t -2/3 1/3 1/3 -2/3 1/3 1/2 1/2 1/2 1/2 1/2 stabil verschieden verschieden verschieden verschieden ? 2/3 -2/3 1/2 verschieden EICHBOSONEN ? 0 ~ 83 000 1 ~ 93 000 0 0 0 LEPTONEN 0,511 -1 +1 105,6 -1 +1 1784 -1 +1 ? 0 0 Elektron Müon Tau ElektronNeutrino MüonNeutrino TauNeutrino eµτνe e+ µ+ τ+ νe νµ νµ ? 0 ντ ντ ? 0 p n Λ Σ+ p n Λ Σ + 938,3 939,6 1115 1189 Σ- Σ - 1197 -1 Σ0 Σ 0 1192 ΞΞ0 Ω- Ξ Ξ 0 Ω - Λc Λc Pionen Pionen Kaonen Kaonen J / Psi D-Null D-Plus Ypsilon π0 π+ K0 K+ J/Ψ D0 D+ Y Tabelle 3-1 Seite 3-12 π- K 0 K- QUARKS 2/3 -1/3 -1/3 2/3 -1/3 γ W+ Z g Proton Neutron Lambda SigmaPlus SigmaMinus SigmaNull Xi-Minus Xi-Null OmegaMinus CharmLambda mittlere Lebensdauer [s] ~5 ~ 10 ~ 100 ~ 1500 ~ 4700 Photon W-Teilchen Z-Teilchen Gluon W- Spin 1 -1 1 1 stabil 10-25 10-25 stabil 1/2 1/2 1/2 1/2 stabil 2 . 10 -6 3 . 10-13 stabil ? 0 1/2 stabil ? 0 1/2 stabil ? BARYONEN +1 -1 0 0 0 0 1 1 uud ddu uds uus uud ddu uds uus 1/2 1/2 1/2 1/2 stabil ca. 900 2,6 . 10-10 8 . 10-11 -1 dds dds 1/2 1,5 . 10-10 0 0 uds uds 1/2 6 . 10-20 1321 1315 1672 -1 0 -1 1 0 -1 dss uss sss dss uss sss 1/2 1/2 1/2 1,6 . 10-10 3 . 10-10 8 . 10-11 2280 1 1 udc udc 1/2 2 . 10-13 uu ud ds us dd du d s su cc cu cd bb 0 0 0 0 1 0 0 1 135 140 498 494 3098 1863 1863 9460 MESONEN 0 0 +1 -1 0 0 +1 -1 0 0 1 0 Elementarteilchen und Quarks 8 . 10-17 2,6 . 10-8 -10 10 / 5 . 10-8 1,2 . 10-8 1 . 10-20 1 . 10-12 4 . 10-13 1 . 10-20 *Teilchen mit sind sogenannte Anti-Teilchen Kapitel 3 Naturwissenschaftliche Grundlagen Kernspaltung Trifft ein thermisches Neutron auf ein U-235 Atom (oder auf bestimmte andere spaltbare Stoffe), so kann es zu einer spontanen Kernspaltung kommen. Aus der Kernspaltung entstehen zwei Spaltprodukte und im Mittel ein bis zwei Neutronen, die ihrerseits wieder ein weiteres U-235 Atom spalten könnten. Die Spaltung von U-235 tritt jedoch nur dann auf, wenn die Neutronen sich nicht zu schnell fortbewegen, d.h. ihre Energien im thermischen Bereich (ca. 0,025 eV) liegen. Bei jeder Spaltung werden dann wieder Neutronen frei, die ihrerseits eine erneute Spaltung bewirken können. Dieser Vorgang unterhält sich selbst und wird deshalb auch als Kettenreaktion bezeichnet. Damit in einer Masse aus U-235 also eine Kettenreaktion stattfinden kann, müssen die schnellen Spaltneutronen durch geeignete Materialien (Moderatoren) abgebremst werden, außerdem muss auch die Masse groß genug sein, damit die Neutronen nicht nach außen entweichen. Die Mindestmasse, bei der eine Kettenreaktion eintreten kann, wird als kritische Masse bezeichnet. Sie beträgt bei U-235 etwa 50 kg, wenn das Metall in Kugelform vorliegen würde und die Neutronen unmoderiert (und unreflektiert) würden. Die kritische Masse lässt sich verringern, wenn der spaltbare Stoff von einem Reflektor (z.B. Graphit, Beryllium, D2O, etc.) umgeben ist, der die Eigenschaft hat, entwichene Neutronen in die kritische Masse zurückzulenken. Da in der natürlichen Umgebungsstrahlung stets freie Neutronen vorkommen, würde in einer kritischen Masse sofort immer eine Kettenreaktion ausgelöst werden. Für den Strahlenschutz sind deshalb beim Umgang mit radioaktiven Stoffen besondere Maßnahmen zu beachten, die alle darauf hinauslaufen, dass auf keinen Fall kritische Bedingungen entstehen. Hierzu ist eine spezielle Ausbildung erforderlich. Abbildung 3-9 Die nukleare Kettenreaktion Seite 3-13 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Grundlagen der Strahlenphysik Ionisierende Strahlung Sogenannte ionisierende Strahlung entsteht beim Zerfall von Radionukliden. Die dabei freigesetzten Strahlungsteilchen können verschiedene Wechselwirkungen mit Materie eingehen: 1. 2. 3. 4. Abbremsung der Strahlungsteilchen und daraus resultierende Wärmeentwicklung; Anregung von Hüllenelektronen; Ionisierung von Hüllenelektronen; Materialisierung von elektromagnetischen Strahlungsteilchen. Strahlen, die eine Ionisierung beim Auftreffen auf Materie hervorrufen können, werden deshalb ionisierende Strahlen genannt. Es werden energiereiche elektrisch geladene Materieteilchen als direkt ionisierende Strahlung bezeichnet, elektrisch neutrale Teilchen oder Photonen als indirekt ionisierende Strahlung. Hinsichtlich der Natur der Strahlung unterscheidet man zwischen Materiestrahlung (Korpuskularstrahlung) und Wellenstrahlung: Materiestrahlung n-Strahlung p-Strahlung α-Strahlung β-Strahlung Neutronen Protonen He2+-Teilchen Elektronen, Positronen γ-Strahlung X-Strahlung elektromagnetische Schwingungen, Photonen elektromagnetische Schwingungen, Photonen Wellenstrahlung Tabelle 3-2 Eigenschaften ionisierender Strahlung Der radioaktive Zerfall Aktivität Elemente, in deren Kern das Zahlenverhältnis von Protonen zu Neutronen unausgewogen ist, sind instabil und zerfallen durch auftretende Kernreaktionen unter Aussendung von Strahlung (wie in der Tabelle 2-2 angegeben). Diese Phänomene werden als Radioaktivität oder radioaktiver Zerfall bezeichnet. Die Strahlung entsteht dadurch, dass die Radionuklide Masse- und Energieportionen mit hoher Geschwindigkeit ausschleudern, welche die ionisierende Strahlung bilden. Ein radioaktiver Zerfall findet u.U. in mehreren Schritten solange statt, bis das entsprechende Radionuklid in ein Seite 3-14 Kapitel 3 Naturwissenschaftliche Grundlagen stabiles Nuklid übergegangen ist (radioaktive Zerfallsreihe). Die Ursache für den radioaktiven Zerfall ist somit das Streben nach dem energetisch günstigsten Zustand eines Atomkerns. UNTER DER AKTIVITÄT EINES RADIONUKLIDS VERSTEHT MAN DIE ZAHL DER ZERFÄLLE PRO ZEITEINHEIT. DIE EINHEIT DER AKTIVITÄT IST DAS BECQUEREL (1 Bq = 1 ZERFALL PRO SEKUNDE). Beispiel: 1 g des Elementes Radium hat eine Aktivität von 3,7 . 1010 Bq = 1 Curie (Ci) Beim Zerfall eines Radionuklids kann auch eine spontane Spaltung (spontaneous fission, sf) des Atomkerns in verschiedene Bruchstücke auftreten. Typisches Beispiel für ein solches instabiles natürliches Radionuklid ist das Uran-235. Der Zerfall des Uranatoms wird durch ein kosmisches Neutron, das auf ihn trifft, ausgelöst. Den Zerfallsprozess kann man sich als eine Reihe von Schwingungen vorstellen, die der getroffene Kern durchläuft, bis er sich schließlich nicht mehr stabilisieren kann und in zwei Teile zerfällt (Kernspaltung). Abbildung 3-10 Die Kernspaltung Entsprechend lässt sich auch eine künstlich induzierte Kernspaltung durchführen. Die Art des Zerfalls, die Lebensdauer und Häufigkeit der Radionuklide lassen sich aus den Radionuklid-Tabellen ermitteln. Zerfallsarten und Zerfallsreihen Je nach Art des entstehenden Zerfallsproduktes unterscheidet man verschiedene Zerfallsarten; Für ein Mutternuklid mit der Ordnungszahl Z und der Massenzahl M findet man folgende wichtige Zerfallsarten: Seite 3-15 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Zerfallsart α - Zerfall β− - Zerfall β+ - Zerfall γ - Zerfall Spontanspaltung Massenzahl Tochternuklid M–4 M M M Ca. ½M Tabelle 3-3 Ordnungszahl Tochternuklid Z-2 Z+1 Z-1 Z variiert Radioaktive Zerfälle - Verschiebungssätze α- und β-Zerfälle sind sehr häufig von γ-Emissionen begleitet. Diejenigen Radionuklide, die durch derartige Zahlengesetze verbunden sind bezeichnet man als Zerfallsreihen. Analysiert man die Nuklidkarte bezüglich dieser Zahlengesetze (sog. Verschiebungssätze), so findet man, dass es insgesamt 4 verschiedene Zerfallsreihen gibt, durch welche die verschiedenen Nuklide entstanden sind: 1. 2. 3. 4. Thorium-Zerfallsreihe Neptunium-Zerfallsreihe Uran-Radium-Zerfallsreihe Actinium-Zerfallsreihe Diese Zerfallsreihen werden jeweils nach dem langlebigsten Vertreter bezeichnet. Eine Besonderheit ist, dass die Neptunium-Zerfallsreihe erst durch die Entdeckung der künstlichen Radioaktivität aufgeklärt wurde. Das radioaktive Zerfallsgesetz DAS ZEITINTERVALL, INDEM SICH DIE ANZAHL DER ATOME EINES RADIONUKLIDS AUF DIE HÄLFTE VERRINGERT HAT, WIRD AUCH ALS DIE HALBWERTSZEIT DES RADIONUKLIDS BEZEICHNET. SIE IST FÜR DAS BETREFFENDE RADIONUKLID EINE CHARAKTERISTISCHE GRÖßE. Seite 3-16 Kapitel 3 Naturwissenschaftliche Grundlagen Radionuklid H-3 Ra - 226 I - 131 Cs - 134 U - 235 U - 238 * sf Häufigkeit 0,00013 % 0,720 % 99,28 % Zerfallsart Halbwertszeit t1/2 12,346 a βα/γ 1,6 . 103 a 8,04 d β /γ 2,06 a / 2,09 h β/γ − 7,030 . 108 a α, β , γ, sf * 4,468 . 109 a α, β−, sf bedeutet „spontaneous fission“ Tabelle 3-4 = Spontan Spaltung Beispiele für radioaktive Zerfälle Der radioaktive Zerfall gehorcht den Gesetzen der Statistik. Die Ursache für die unterschiedlichen Halbwertszeiten verschiedener Radionuklide lässt sich dadurch erklären, dass für jeden radioaktiven Zerfall zunächst eine Energiebarriere existiert bevor der energetisch günstige Zustand erreicht wird. Die Zerfallswahrscheinlichkeit hängt von der Lage der Energiezustände des Kerns vor und nach Zerfall ab, sowie von der Höhe der Barriere. A t Abbildung 3-11 Die Aktivitätsabnahme eines Radionuklids Abbildung 2-11 zeigt die jeweils verbleibende Aktivität eines Radionuklids nach einer Halbwertszeit (= 1 Balkenbreite). Der Verlauf der Aktivitätsabnahme mit der Zeit wird durch eine Exponentialfunktion beschrieben. Dieser zeitliche Verlauf des radioaktiven Zerfalls wird als radioaktives Zerfallsgesetz bezeichnet: A ( t ) = A 0 ⋅ e − λ⋅ t A(t) = Aktivität zum Zeitpunkt t, t = Zeitspanne nach t = 0, λ= A0 = Ausgangsaktivität t = 0, t 1/2= Halbwertszeit ln 2 t1/ 2 λ = Zerfallskonstante, Seite 3-17 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Die Zerfallskonstante λ ist ein Maß für die Zerfallswahrscheinlichkeit. Häufig wird auch die mittlere Lebensdauer τ eines Radionuklids angegeben, diese errechnet sich aus dem Kehrwert der Zerfallswahrscheinlichkeit: τ= 1 λ DIE LEBENSDAUER EINES RADIONUKLIDS IST DIEJENIGE ZEIT, INDER DER ANTEIL DER ATOME AUF DEN E-TEN TEIL DER AUSGANGSMENGE ZURÜCKGEGANGEN IST. Viele Radionuklide bilden nach ihrer Umwandlung Tochterkerne, die wiederum radioaktiv sind. So wandelt sich Ra-226 in das radioaktive Edelgas Rn-222 um. Aktivitätsangaben für ein Radionuklid beziehen sich aber immer auf die Ausgangssubstanzen, nicht auf die beim Älterwerden angesammelten Folgeprodukte. Entsprechend ist auch bei der Anwendung des radioaktiven Zerfallsgesetzes zu differenzieren. Die Aktivität eines Nuklidgemisches, das verschiedene Vertreter einer Zerfallsreihe, enthält kann nicht nach dem einfachen Zerfallsgesetz berechnet werden. Zur Berechnung der Gesamtaktivität eines Nuklidgemisches muss das radioaktive Zerfallsgesetz modifiziert werden. Zerfallsdiagramme Zur Beschreibung der Energiezustände, die ein Nuklid durchlaufen kann, benutzt man Energiediagramme, ähnliche den Energieschemata der Elektronen. Alle Zustände, Energiegehalte und Zerfallswahrscheinlichkeiten für eine bestimmte Zerfallsart können aus diesen Diagrammen abgelesen werden. Dem Diagramm kann man den quantenmechanischen Kernzustand (z.B. +5) entnehmen, die Energie dieses Zustandes (z.B. 0 = Grundzustand), die Halbwertszeit des Zustandes (z.B. 5,3 y = 5,3 Jahre), die Wahrscheinlichkeit eines Übergangs (z.B. 99 %) und die γ-Energie, die einem Übergang entspricht (Energie des abgestrahlten Photons, z.B. 1172 keV). Zerfallsdiagramme lassen sich aus Standardwerken der Physik ermitteln, oder sind auf CD-ROM verfügbar, für die vorliegenden Darstellungen wurde die CD von Wiley-Interscience (8. Auflage, Version 1, März 1996) verwendet. Seite 3-18 Kapitel 3 Naturwissenschaftliche Grundlagen Abbildung 3-12 Vereinfachtes Zerfallsdiagramm I für Co-60 Abbildung 3-13 Vereinfachtes Zerfallsdiagramm II für Co-60 Abbildung 3-14 Vereinfachtes Zerfallsdiagramm III für Co-60 Seite 3-19 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Spezifische Aktivität Die Aktivität einer Probe steigt mit der Probenmenge. Deshalb wird die sog. spezifische Aktivität eingeführt: DIE SPEZIFISCHE AKTIVITÄT IST DIE AKTIVITÄT PRO MASSE IN Bq / KG Angaben zur spezifischen Aktivität können sich auf verschiedene, in der Substanzmenge enthaltenen Radionuklide beziehen, deshalb muss immer eine entsprechende Angabe gemacht werden. Bei der experimentellen Bestimmung der Gesamtaktivität wird zunächst eine radionuklidspezifische Analyse durchgeführt. Die meisten Radionuklide senden beim Zerfall γ-Quanten mit charakteristischen Energien aus. Diese Energien kann man mit Hilfe γ-spektroskopischer Methoden ermitteln und aus Nuklidbibliotheken die zugehörigen Nuklide bestimmen. Massenbezogene Aktivitäten verwendete man z.B. nach dem Reaktorunfall von Tschernobyl um die Belastung in Lebensmitteln zu kennzeichnen. Spezifische Aktivität 1,0 0,3 8,0 ≈ 820 Tabelle 3-5 Lebensmittel Rindfleisch, Kalbfleisch Schwein Schaf Reh, Hirsch u.a. Wild Cs-134 / Cs-137 Gehalt in Fleisch (BRD 1990) Angaben in Bq / kg Oberflächenaktivität Flächenbezogene Aktivitäten (sog. Oberflächenaktivitäten) werden angegeben um die Kontamination von Oberflächen zu bestimmen, wenn diese durch offene radioaktive Stoffe kontaminiert wurden. Für Kontaminationskontrollen wurden eigens Kontaminationsmonitore entwickelt. DIE OBERFLÄCHENAKTIVITÄT IST DIE AKTIVITÄT PRO FLÄCHE: Bq / cm2 Seite 3-20 Kapitel 3 Naturwissenschaftliche Grundlagen Beispiel aus der StrlSchV §44 Anlage III: Grenzwert der Flächenkontamination am Arbeitsplatz (im Kontrollbereich, gemittelt über 100 cm2 eines β-Strahlers, wie z.B. P-32 =100 Bq / cm2, S-35 =100 Bq / cm2, I-125 =10 Bq / cm2 Aktivität pro Volumen Eine volumenbezogene Aktivität kann z.B. angegeben werden, wenn die Radioaktivität des Abwassers oder der Abluft einer nuklearen Einrichtung beschrieben werden soll. BEI RADIOAKTIVEN GASEN GIBT MAN AKTIVITÄT PRO VOLUMEN IN Bq / m3 Beispiel: Die durchschnittliche Radonbelastung in Innenräumen beträgt 50 Spitzenbelastungen ≥ 200 AN Bq / m3 Bq / m3 Strahlungsarten α - Strahlung Die beim radioaktiven Zerfall ausgesandten α-Teilchen haben bei Austritt aus dem Atomkern Geschwindigkeiten von etwa 15 000 km / s. Sie werden innerhalb weniger cm durch Stöße mit Luftmolekülen abgebremst. Schließlich fangen die langsamen Helium-Ionen Elektronen aus der Umgebung ein und existieren weiter als Edelgas. Das Beispiel zeigt den Zerfall von Radium. Zerfallsprodukt ist das radioaktive Edelgas Radon. Abbildung 3-15 Der α - Zerfall Seite 3-21 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Eigenschaften von α - Strahlung: Eigenschaften Teilchenart: Radionuklide: Energie: Reichweite(Luft): Energieverteilung: Ww* mit Materie: Gefahr: Schutz: Nachweis: He-4 Kerne Pu-239, Ra-226, Rn-222, Am-241, Po-210, U-235 MeV – Bereich bei 5 MeV ca. 3,5 cm diskretes Linienspektrum Ionisation, Anregung Inkorporation (Inhalation, Ingestion) Papier, Abstand >10 cm Proportionalzählrohr, Ionisationskammer, Geiger-Müller-Zählrohr, Halbleiter-Detektor, jeweils dünnwandig * Ww bedeutet Wechselwirkung Tabelle 3-6 Eigenschaften von Alpha-Strahlung Beispiel: Es hat sich gezeigt, dass in manchen Gebieten Deutschlands, wie z.B. dem Erzgebirge oder dem Schwarzwald erhöhte Konzentrationen des Gases Radon auftreten. Dieses tritt als radioaktives Zerfallsprodukt bei uran- bzw. radiumhaltigen Erzen auf. In entsprechend gelegenen Kellerräumen können sich dann ungewöhnlich hohe Radonkonzentrationen einstellen, die gesundheitsbedrohend sind. Die Ermittlung der Radonkonzentration in der Luft stellt ein sehr spezielles messtechnisches Problem dar. Meist wird die von den Tochternukliden ausgesandten α - Strahlung mit Oberflächensperrschichtdetektoren gemessen. Die aus dem Spektrum abgeleitete Häufigkeit der kurzlebigen radioaktiven Folgeprodukte ergibt dann ein Maß für die Konzentration der Radon-Isotope in der Luft. β - Strahlung Protonen und Neutronen im Kernverband haben die Möglichkeit, ihre charakteristischen Eigenschaften auszutauschen, wobei Elektronen bzw. Positronen aus dem Kern emittiert werden und das ganze System in einen stabilen Zustand übergeht. Beim β−- Zerfall wird aus dem Kern eines Radionuklids ein Elektron abgegeben, welches eine Geschwindigkeit zwischen Null und Lichtgeschwindigkeit bei Austritt aufweist. Diese Elektronen bilden dann die β−- Strahlen. Da nach dem Aussenden des Elektrons der Kern ein Proton mehr besitzt, erhöht sich beim Radionuklid die Kernladungszahl um 1 (Elementumwandlung), während die Massenzahl erhalten bleibt. Beim selteneren β+Zerfall wird aus dem Kern ein Positron, β+, abgegeben.. Entsprechend wird die Kernladungszahl dabei um eines vermindert. Das Spektrum von Beta-Teilchen erstreckt sich über einen kontinuierlichen Bereich (Unterschied zu Elektronenstrahlen!). Da nach dem Energieerhaltungssatz dem BetaZerfall eine diskrete Energiemenge entspricht muss die "fehlende" Energie an ein elektrisch neutrales Neutrino abgegeben werden: n → p + e- + υ Seite 3-22 bzw: p → n + e+ + υ Kapitel 3 Naturwissenschaftliche Grundlagen Eigenschaften von β - Strahlung Eigenschaften Teilchenart: Radionuklide: Energie: Reichweite(Luft): Energieverteilung: Ww mit Materie: Gefahr: Schutz: Nachweis: Elektronen, Positronen H-3, C-14, Sr-90, Cs-137 , Tl-204, Co-60 keV ... MeV bei 1 MeV ca. 4 m kontinuierliches Spektrum Ionisation, Anregung, Bremsstrahlung Hautexposition, Inkorporation Abschirmung mit Al, PMMA, etc. Proportionalzählrohr, Ionisationskammer, Geiger-Müller-Fensterzählrohr, jeweils dünnwandig Tabelle 3-7 Eigenschaften von Bestrahlung Abbildung 3-16 Der β - Zerfall γ - Strahlung Bei vielen Kernumwandlungen stabilisiert sich der entstandene angeregte Tochterkern, indem er seine überschüssige Energie in Form einer zusätzlichen energiereichen elektromagnetischen Strahlung (γ - Strahlung) abstrahlt. Abgesehen von der Art der Entstehung ist sie praktisch identisch mit der Röntgenstrahlung (X - Strahlen). Diese beiden Strahlungen - wie auch das sichtbare Licht - treten in einzelnen Portionen (Photonen, Quanten) auf. Die γ - Quanten bewegen sich konstant mit der Vakuumlichtgeschwindigkeit von 299 792,5 km/s. Durch den γ - Zerfall ändert sich der Energieinhalt des Kerns, nicht aber seine Massen- oder Ladungszahl. γ - Strahlung lässt sich (unspezifisch) nachweisen durch Schwärzung, die sie auf unbelichteten Filmen hervorruft. Mit Hilfe der γ - Spektroskopie (z.B. mit Halbleiterdetektoren) können die genauen Energien der Photonen registriert werden, und es kann die radionuklidspezifische Energieanalyse durchgeführt werden. Seite 3-23 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Der γ-Zerfall Abbildung 3-17 Eigenschaften von γ - Strahlung: Eigenschaften Teilchenart: Radionuklide: Energie: Reichweite: Energieverteilung: Ww mit Materie: Gefahr: Schutz: Nachweis: *m Photonen Am-241, Co-60, I-131, Ba-133, Ba-137m, Tc-99m* keV ... MeV theoretisch ∞ diskretes Linienspektrum Streuung, Photoeffekt, Comptoneffekt, Paarbildung Körperexposition, Inkorporation Abschirmung mit Pb Proportionalzählrohr, Ionisationskammer, Geiger-Müller-Zählrohr, Szintillationszähler, Halbleiter-Detektor, jeweils indirekter Nachweis ! bedeutet metastabil, d.h. der Kern befindet sich im angeregten Zustand Tabelle 3-8 Eigenschaften von Gamma-Strahlung Neutronenstrahlung n Freie Neutronen sind instabil und zerfallen mit einer Halbwertszeit von 11,5 Minuten. Der Zerfall besteht entweder in der Umwandlung in ein Proton oder in der Anlagerung an andere kosmische Nuklide (Neutroneneinfang), die dadurch meist radioaktiv werden. In der Natur entstehen Neutronen, wenn die kosmische Höhenstrahlung (p, He) auf N- bzw. O-Atome der Atmosphäre treffen und Kernreaktionen eintreten. Außerdem entstehen Neutronen bei der (spontanen und induzierten) Spaltung schwerer Kerne. Aber auch durch Kernreaktionen mit leichten Elementen lassen sich Neutronen erzeugen. Bei bestimmten Materialien wie Li und Be lassen sich durch Kombination eines αStrahlers mit dem Material regelrechte Neutronenquellen konstruieren: 9 4 Be + 42 α → 12 6 C + 01 n Neutronen entstehen auch bei Kernfusionsreaktionen, wie sie z.B. in der Sonne ablaufen: Seite 3-24 Kapitel 3 Naturwissenschaftliche Grundlagen 2 1 D + 31 T → 42 He + 01 n + 17,58 MeV Entsprechend ihrer kinetischen Energie unterscheidet man folgende Arten von Neutronen: Langsame Neutronen: Mittelschnelle Neutronen: Schnelle Neutronen 10 eV 10 eV > kinetische Energie < kinetische Energie < 0,1 MeV kinetische Energie > 0,1 MeV Thermische Neutronen: kinetische Energie = 0,0253 eV bei 293,16 K Geschwindigkeit = 2 200 m/s bei 293,16 K Röntgenstrahlen Röntgenstrahlen, auch X-Strahlen genannt, bestehen aus Photonen und weisen damit ähnliche Eigenschaften wie γ-Strahlen (in Abhängigkeit ihrer Energie) auf. Im Gegensatz zu γ-Strahlen entstehen X-Strahlen, wenn geladenen Teilchen, wie z.B. Elektronen in metallischen Substanzen abgebremst werden oder durch Elektronenübergänge in den inneren (kernnahen) Elektronenschalen. Entsprechend unterschiedliche Arten von Röntgenstrahlungen treten dann auf: • Bremsstrahlung Die Bremsstrahlung entsteht, wenn ein geladenes Teilchen (z.B. Elektron aus Glühkathode) abgebremst oder auch beschleunigt wird. Die Energiedifferenz wird als elektromagnetische Strahlung ausgesandt. Beim Eintreten in Materie können beschleunigte Elektronen im COULOMB-Feld des Atomkerns abgebremst werden, wobei die abgegebene Energie proportional zum Quadrat der Kernladungszahl ist. Bremsstrahlung wird daher umso wahrscheinlicher je höher die Ordnungszahl der abbremsenden Materie ist. Das Spektrum erweist sich als kontinuierlicher energetischer Bereich (Kontinuum). • Charakteristische Röntgenstrahlung Beim Herausschlagen von Elektronen der inneren Schalen entstehen "Löcher", welche durch z.B. Valenzelektronen sofort wieder besetzt werden. Die damit verbundenen Energieübergänge entsprechen diskreten (charakteristischen) Spektrallinien, die auch für analytische Zwecke ausgenutzt werden können. Seite 3-25 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Strahlenschu Abbildung 3-18 Röntgenspektrum einer Wolframanode Ein Röntgenspektrum weist also immer zwei Bereiche auf, den Bereich der Bremsstrahlung und manchmal überlagert - den Bereich charakteristischer Röntgenspektrallinien. Aus der Messung der Energie der charakteristischen Röntgenfluoreszenzstrahlung kann man bei der RöntgenfluoreszenzRöntgenfluoreszen spektroskopie eine Analyse der (metallischen) Bestandteile einer bestrahlten Probe durchführen und so z.B. zerstörungsfrei die Bestandteile einer Legierung ermitteln. In der medizinischen Diagnostik wird meist die Bremsstrahlung verwendet, außer bei der Mammographie, dort wird der charakterischarakteri tische Strahlungsanteil (wegen gen der geringen Gewebekontraste) eingesetzt. Andere Zerfallsarten Elektroneneinfang ("electron capture") Neben den oben angegebenen Zerfallsarten gibt es auch noch Zerfälle, die dadurch zustande komko men, dass ein Atomkern Elektronen aus den benachbarten benachbarten inneren Schalen (K, oder L) einfängt, dadurch entsteht aus einem Proton ein Neutron. Dieser K-Einfang wird mit K gekennzeichnet. Anschließend wird das entstandene Loch in der inneren Elektronenhülle durch Elektronensprung eines äußeren Hüllenelektrons aufgefüllt, fgefüllt, begleitet von entsprechender Emission einer charakteristischen Strahlung. Beispiel: 125 53 ec J → 125 52 Te + 28 keV Bei leichten Atomen wird die durch den Elektronensprung freigesetzte Energie häufig auf ein VaV lenzelektron desselben Atoms übertragen, welches welches an Stelle des Röntgenquants emittiert wird. DerDe artige Elektronen werden als Auger-Elektronen Auger bezeichnet. Spezielle Techniken in der OberfläOberfl chenanalytik erlauben die Messung solcher Auger-Elektronen Auger (Auger-Spektroskopie). Spektroskopie). Seite 3-26 Kapitel 3 Naturwissenschaftliche Grundlagen Isomere Übergänge und Konversionselektronen Bei der Mehrzahl aller Alpha- bzw. Beta-Zerfälle ist der Grundzustand des betreffenden Nuklids nicht erreicht, weshalb diese Zerfälle von Gamma-Emissionen begleitet sind. Die Lebensdauer eines solchen „angeregten“ Atomkerns kann im Femtosekundenbereich bzw. bei einigen Tagen liegen. Bei langlebigen Zuständen spricht man von Isomeren, gekennzeichnet durch den Buchstaben m (metastabil). Entsprechende Übergänge werden auch als isomere Übergänge bezeichnet. Dieser Prozess wird mit I gekennzeichnet. Sogenannte Konversionselektronen können entstehen, wenn der angeregte Atomkern seine Anregungsenergie auch auf Hüllenelektronen überträgt, so dass bei diesem Prozess (innere Konversion) anstelle von γ-Quanten die Konversionselektronen emittiert werden. Im Gegensatz zu echter β-Strahlung sind die Konversionselektronen monoenergetisch. Sie werden mit e- gekennzeichnet und sind für ein betreffendes Nuklid charakteristisch. Wechselwirkung von Strahlung mit Materie Energieübertragung und Strahlenwirkung Lineare Energieübertragung Direkt und indirekt ionisierende Strahlung wird in der Materie durch unterschiedliche Mechanismen geschwächt. Auch sind bei Korpuskularstrahlung und bei elektromagnetischer Strahlung die Wechselwirkungsmechanismen unterschiedlich. Direkt ionisierende Teilchen können beim Vorbeifliegen an der Atomhülle eines Atoms dort Elektronen befreien. Bei jeder dieser Ionisationen verlieren die Korpuskeln selber wieder so viel Energie, dass sie am Ende bis auf thermische Energien abgebremst werden. Geladene Korpuskeln haben somit in Materie eine genau angebbare Reichweite. Diese Reichweite nimmt von Elektronen zu Protonen zu Deuteronen zu Alpha-Teilchen und schließlich zu schweren Spaltfragmenten laufend ab. Elektrisch neutrale Teilchen wie Neutronen können durch Stoßprozesse mit Atomkernen abgebremst werden, wobei manche Rückstoßkerne ihrerseits direkte Ionisation benachbarter Atome hervorrufen können. Genügend abgebremste Neutronen können schließlich von einem anderen Kern eingefangen werden, dieser Einfang wird auch als Aktivierung bezeichnet, da entstehende Nuklide meist radioaktiv sind. Elektromagnetische Strahlung wechselwirkt mit Materie, indem Atome angeregt bzw. ionisiert werden. Die sekundär erzeugten geladenen Teilchen übertragen dann die Energie. Wenn ionisierende Strahlung mit Materie wechselwirkt, werden die daraufhin eintretenden Prozesse in folgende Stadien eingeteilt: 1. Physikalische Phase: 10-18 - 10-12 s nach Eintritt in Materie; z.B. Wechselwirkung eines energiereichen Teilchens mit einem Wassermolekül, was zur Energieabgabe führt; Seite 3-27 S. Prys / E. Foßhag Fachkunde im Strahlenschutz 2. Physikochemische Phase: 10-12 - 10-9 s nach Eintritt in Materie; das ionisierte bzw. angeregte Wassermolekül gibt Energie an die Umgebung ab, zerfällt oder erfährt andere molekulare Veränderungen und geht schließlich in einen Grundzustand über. Während dieser Phase bilden sich freie Radikale; 3. Chemische Phase: 10-9 - 100 s nach Eintritt in Materie; Die gebildeten Radikale reagierend mit benachbarten Molekülen, z.B. mit Biomolekülen; 4. Biologische Phase: 100 - 109 s nach Eintritt in Materie; stabilisierte irreparable molekulare Schäden führen zu biologischen Effekten, wie Zelltod, genetischen Veränderungen, zu Missbildungen während der Embryogenese und zu Krebs. ALLE GELADENEN TEILCHEN HÖHERER ENERGIE LÖSEN IN GASFÖRMIGER, FLÜSSIGER ODER FESTER UMGEBUNG IONISATIONSVORGÄNGE AUS, WOBEI SIE IHRE ENERGIE PORTIONSWEISE VERLIEREN UNTER DER SPEZIFISCHEN IONISATION EINES STRAHLUNGSTEILCHENS VERSTEHT MAN DIE ANZAHL DER GEBILDETEN IONENPAARE PRO MM W EGSTRECKE CERENKOV-STRAHLUNG TRITT IMMER DANN AUF, WENN SICH GELADENE TEILCHEN IM SCHNELLER AUSBREITEN KÖNNEN ALS LICHTTEILCHEN (PHOTONEN) IN DIESEM MEDIUM. MEDIUM Die Ionisationsbremsung geladener Teilchen (auch Sekundärteilchen) ist auf Anregung und Ionisation umgebender Materie zurückzuführen. Die Ionisationswirkung hängt nicht nur von der Größe der herrschenden Kräfte ab, sondern auch von der Zeitdauer der Einwirkung, Aus diesem Grunde können langsame geladene Teilchen stärker ionisieren als schnelle Teilchen. Ein Maß für die Strahlenwirkung ist die Energie, die pro Weglänge in Materie übertragen wird. Der spezifische (mittlere) Energieverlust E entlang einer Wegstrecke x lässt sich in drei Anteile aufspalten: Seite 3-28 Kapitel 3 Naturwissenschaftliche Grundlagen − dE dE dE dE = − + − + − dx dx I dx K dx S I Energieabnahme E pro Weg x durch Ionisation K Energieabnahme E pro Weg x durch Zusammenstöße mit Atomkernen S Energieabnahme E pro Weg x durch elektromagnetische Strahlung Von praktischer Bedeutung, weil am wahrscheinlichsten, ist nur der erste Term. Er hängt sowohl von den Eigenschaften der geladenen Teilchen (Ladung, Geschwindigkeit, Energie) als auch von denen des abbremsenden Stoffes (Dichte, Ionisierungsenergie) ab. Andere Bezeichnungen für den spezifischen Energieverlust pro Weg sind das (Ab)Bremsvermögen, die lineare Energieübertragung, bzw. linear energy transfer , LET. Der Zusammenhang zwischen spezifischem Energieverlust und spezifischer Ionisation ist gegeben durch: dI p dE ⋅ W = − dx I dx Ip = Zahl der Ionenpaare W = Ionisierungsenergie In Tabelle 2-9 werden Werte für LET für verschiedene Strahlenarten angegeben. Der größere LETWert energieärmerer Photonenstrahlung hängt mit der geringeren Geschwindigkeit der Comptonelektronen zusammen. Weniger energiereiche Elektronen zeigen pro Wegstreckeneinheit häufiger eine Wechselwirkung und hinterlassen somit eine höhere Ereignisdichte (Ionisation, Anregung). Diese Eigenheit wird auch bei den anderen Strahlenarten beobachtet. Abbildung 3-19 Darstellung von Ionisierungsereignissen entlang eines Weges für verschiedene Strahlenarten Seite 3-29 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Strahlenart 250 3 1,2 - 1,3 4,0 0,6 10 1 2,5 19 Tabelle 3-9 keV Röntgenstrahlung MeV Röntgenstrahlung MeV Co-60 – γ − Strahlung MeV α - Strahlung keV Beta-Teilchen aus T keV Beta-Teilchen MeV Beta-Teilchen MeV Neutronen MeV Neutronen LET [keV/µm] 3,0 0,3 0,3 55,4 5,5 2,3 0,25 10 7 Mittleres lineares Energieübertragungsvermögen LET einiger Strahlenarten in Wasser Die Abhängigkeit des LET von der Energie eines schweren Teilchens (z.B. Protonen oder AlphaTeilchen) wird in Abbildung 2-20 angedeutet. Für diese Teilchen ist am Anfang ihrer Bahn nur eine kleine Ionisationsdichte zu erwarten, weil die Teilchen sehr hohe Geschwindigkeiten haben. Gegen Ende der Bahn hat die Geschwindigkeit abgenommen und die Ionisierungsdichte nimmt stark zu. Es entsteht ein charakteristisches Ionisationsmaximum (Bragg-Peak). Entsprechende Kurven werden auch als "Bragg-Kurven" bezeichnet. Abbildung 3-20 LET für Alpha-Teilchen verschiedener Energien in Wasser in Abhängigkeit ihrer Eindringtiefe Bei der Betrachtung der Wechselwirkungsprozesse von Alpha-Teilchen mit Materie muss auch die Dichte des umgebenden Mediums betrachtet werden. Strenggenommen müsste der differentielle Energieverlust S eines geladenen Teilchens betrachtet werden. In S ist immer die übertragene Energie LET enthalten. Es gilt immer: LET < S. S durchläuft für alle Teilchen ein Minimum im mittleren Energiebereich. Der auf die Dichte ρ eines Materials bezogene differentielle Energieverlust S / ρ wird auch als Massebremsvermögen bezeichnet. Seite 3-30 Kapitel 3 Naturwissenschaftliche Grundlagen S ρ = 1 dE ⋅ ρ dx S = differentieller Energieverlust ρ = Dichte des Materials Das Verhältnis der Massebremsvermögen verschiedener Materialien im Verhältnis zur Luft ist in Standardwerken der Physik tabelliert. Die Energieabsorption, die bei Eintreten von ionisierender Strahlung in Materie stattfindet, ist letztendlich ein Maß für die Strahlendosis. Eine Ei solche Dosisgröße ist die Kerma (= kinetic energy released in matter), matter), diese Dosisgröße wird allerdings nur für Photonen- und Neutronenstrahlung angewandt, die naturgemäß eine größere Reichweite Reichwei haben. DIE KERMA IST DER QUOTIENT AUS DER SUMME DER KINETISCHEN ANFANGSENERGIEN ALLER GELADENEN TEILCHEN, DIE VON INDIREKT IONISIERENDER ION STRAHLUNG IN EINEM VOLUMENELEMENT ERZEUGT WERDEN UND DER MASSE DES VOLUMENELEMENTES. BEI IHRER ANGABE MUß DAS BEZUGSMATERIAL (Z.B. WASSERKERMA SERKERMA) GENANNT WERDEN. Abbildung 3-21 Unterscheidung von Kerma und Energiedosis ( aus Vogt/Schulz Grundzüge des praktischen StrahStra lenschutzes ) Die Radiolyse des Wassers Beim Eindringen ionisierender Strahlung in ein wässriges Medium können nun in der chemischen Phase infolge der Ionisierungen folgende Prozesse, die auch als Radiolyse des Wassers bezeichnet werden, ablaufen: Seite 3-31 S. Prys / E. Foßhag Fachkunde im Strahlenschutz < H 2O → H 2O + + e − Ionisation − kin e H 2O → H 2O * Anregung H 2O + + H 2O → HO • + H 3O + − e − + n ⋅ H 2O → eaq − eaq + H 2O → H • + OH − H 2O* → H • + OH • Reaktionen unter Einwirkung ionisierender Strahlung - wie sie besonders in der Strahlenchemie untersucht werden - kennzeichnet man auch häufig mit einer Pfeilschlange: M M* (strahleninduzierte Anregung) M M+ + e- (strahleninduzierte Ionisierung) Das hydratisierte Elektron eaq- kann je nach Reinheit des Wassers Lebenszeiten bis in den Millisekundenbereich aufweisen. Alle durch Wasserradiolyse entstandenen Radikale können innerhalb ihrer Lebenszeit (10-9 - 100 s) diffundieren um dann schließlich mit anderen Radikalen oder leicht oxidierbaren (Bio)molekülen zu reagieren: H • + H • → H2 H • + OH • → H 2O OH • + OH • → H 2O2 − + 2 H 2O → H 2 + 2OH − 2eaq − eaq + H • + H 2O → H 2 + OH − Die Radiolyse des Wassers ist somit ein wesentlicher Schritt zum molekularen Verständnis biologischer Strahlenwirkungen. Aus den Folgereaktionen der Radiolyse ist ersichtlich, dass als Folge der Bestrahlung aus Wasser das starke Oxidationsmittel H2O2 entstehen kann, das als Zellgift wirkt. Die ablaufenden Prozesse werden sehr stark vom herrschenden pH-Wert eines wässrigen Systems beeinflusst, sowie vom Sauerstoffgehalt, da letzterer zur Bildung von Hydroperoxid HO2 führen kann: − + H 2 O / − OH − eaq + O2 → O2− ← → HO2• ← H • + O2 Seite 3-32 Kapitel 3 Naturwissenschaftliche Grundlagen Wegen ihrer besonderen Reaktivität wird die Bildung der Sauerstoffradikale O2 und HO2 mit als eine der Ursachen für die Strahlenempfindlichkeit anoxischer Zellen betrachtet. Andererseits finden dieselben Ionisationsprozesse, die in biologischer Matrix stattfinden, natürlich auch in anderer Materie statt, sie können z.B. zur Materialversprödung im Bereich hoher Strahlendosen führen. Diese Wechselwirkungsprozesse sind aber auch Grundlage für die Detektion ionisierender Strahlung, wie es in der Strahlenmesstechnik praktiziert wird. Ionisationsprozesse, die in einem Strahlendetektor auftreten, sind die Grundlage für viele Meßverfahren, da sie als elektrische Impulse registriert werden können. Wechselwirkungen von α - Strahlung α - Strahlen und Protonen mit extrem hohen Energien bewirken beim Auftreffen auf Materie Kernreaktionen. Das trifft jedoch nicht für α - Strahlung gewöhnlicher Radionuklide zu. Man beobachtet, dass α - Strahlung besonders schnell von Materie absorbiert wird. In Luft beträgt die Reichweite nur ca. 4 cm, bzw. genügt ein Blatt Papier zur Abschirmung von α - Strahlung! Die Ursache hierfür liegt darin, dass die Wechselwirkungsprozesse zwischen α - Strahlung und der umgebenden Materie sehr stark - d.h. sehr dicht aufeinanderfolgend - ist. Ihre Energie verlieren α - Teilchen durch Ionisationsprozesse längs ihres Weges. Ein α - Teilchen mit einer Ausgangsenergie von 3,5 MeV erzeugt insgesamt längs seines Weges in Luft 105-Ionenpaare. Die Weglänge hierfür beträgt etwa 4 cm (Reichweite). Am Anfang des Weges beträgt die spezifische Ionisation ca. 3000 Ionenpaare pro mm Wegstrecke erzeugt werden, am Ende ca. 7000. (Abb. 2-20). Nach Durchlaufen dieses Weges entsteht aus dem α - Teilchen ein neutrales He-Atom, da es im abgebremsten Zustand Elektronen aus der Umgebung schließlich einfängt. Die Reichweite, bzw. Ionisationsdichte variierte mit der Dichte des umgebenden Mediums. Die Bahn, die ein α - Teilchen zurücklegt verläuft wegen der relativ großen Masse weitgehend gerade. Wechselwirkungen von β - Strahlung β - Strahlen haben - je nach ihrer Energie - im Wesentlichen drei verschiedene Möglichkeiten mit Materie zu wechselwirken: 1. β - Strahlen mit extrem hohen Energien ( MeV - GeV-Bereich, z.B. aus Beschleunigern) erzeugen beim Auftreffen auf Materie Röntgenstrahlung (Wechselwirkung mit Atomkernen); 2. β - Strahlen, wie sie von Radionukliden ausgesandt werden, ionisieren die umgebende Materie (Wechselwirkung mit Elektronen); Seite 3-33 S. Prys / E. Foßhag Fachkunde im Strahlenschutz 3. β - Strahlen können besonders an Atomen mit hohen Ordnungszahlen (wie z.B. Blei) gestreut werden (Rückstreuung). Abschirmung von β - Teilchen erfolgt deshalb vorzugsweise durch Materialien niederer Ordnungszahl. Entstehen beim β - Zerfall eines Radionuklids schnelle Elektronen, so bewegen sich diese auf eher zickzackförmigen Bahnen, da sie wegen der relativ kleinen Masse oft abgelenkt werden. Die Reichweite eines β - Teilchens von ca. 3 MeV beträgt in Luft etwa 10 Meter. Die spezifische Ionisation beträgt nur etwa 4 Ionenpaare pro Millimeter. Die größere Reichweite von β - Teilchen gegenüber α - Teilchen erklärt sich dadurch, dass die lineare Energieübertragung geringer ist. Sie hängt praktisch nur von der Dichte ρ des durchstrahlten Stoffes ab. − dE ~ρ dx Wenn sich β - Strahlen in Wasser oder Plexiglas ausbreiten, so kann man Cerenkov-Strahlung beobachten. Als Absorber für β - Strahlung benutzt man vorzugsweise Stoffe mit geringer Ordnungszahl wie Al oder PMMA (Plexiglas), da sie am wenigsten zur Streuung der β - Strahlen beitragen. Bei Materialien höherer Ordnungszahl, wie z.B. Pb erfahren β - Strahlen eine enorme Streuung, da sie an den vielen Hüllenelektronen des Materials abgelenkt werden. Die Schichtdicke für Absorbermaterialien wird häufig in mg/cm2 angegeben. Abbildung 2-21 zeigt eine Absorptionskurve für β - Strahlen in Aluminium. Bei logarithmischer Auftragung, erkennt man, dass die Schwächung im Material nur annähernd exponentiell verläuft: I = I 0 ⋅ e − µ ⋅d I = geschwächte (ungestreute) Strahlung µ = Absorptionskoeffizient I0 = Ausgangsintensität d = Schichtdicke Abbildung 3-22 Absorptionskurve für Beta-Strahlung, 1,71 MeV in Al Seite 3-34 Kapitel 3 Naturwissenschaftliche Grundlagen Die Absorptionskurve geht in einen nahezu konstanten Endwert über, der durch Bremsstrahlung hervorgerufen wird. Aus der Extrapolation der Absorptionskurve lässt sich die maximale Reichweite von Beta-Strahlung ermitteln. Wechselwirkungen von γ - und Röntgenstrahlung Die Absorption von γ - bzw. X-Strahlung (Photonen) in Materie verläuft grundsätzlich anders als bei Partikeln. Photonen besitzen keine Ladung, ihre Wechselwirkung mit Materie ist daher sehr gering. Während α - bzw. β - Strahlung in vielen Ionisationsschritten portionsweise ihre Energie an die Umgebung abgeben, erfolgt bei Photonen sehr häufig nur ein bzw. wenige Ionisationsschritte, die zur Auslöschung des Photons führen. Deshalb lässt sich auch keine maximale Reichweite angeben. Die Absorption ist auch hier von der Dichte des umgebenden Mediums abhängig und verläuft streng nach einem exponentiellen Schwächungsgesetz: I = I 0 ⋅ e − µ ⋅d I = geschwächte (ungestreute) Strahlung µ = Absorptionskoeffizient I0 = Ausgangsintensität d = Schichtdicke Der Zusammenhang zwischen der Strahlenenergie und der Absorption wird durch die Halbwertsdicke d1/2 charakterisiert: d1 2 = ln 2 µ Abbildung 3-23 Absorption von Gamma-Strahlung in Blei (Cs-137) Seite 3-35 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Mechanismen der Energieabsorption von Photonen Man unterscheidet folgende Mechanismen zur Absorption von Photonen: 1. Photoeffekt bei kleinen Photonen-Energien (vollständige Absorption in der Atomhülle) 2. COMPTONeffekt bei mittleren Photonen-Energien (inkohärente Streuung in der Atomhülle) 3. Paarbildungseffekt bei großen Photonen-Energien (vollständige Absorption im COULOMBFeld des Atomkerns) Neben der Art der Wechselwirkung lassen sich auch Angaben zur Wahrscheinlichkeit des Eintreffen eines bestimmten Prozesses machen. DEM WIRKUNGSQUERSCHNITT σ VERSTEHT MAN DIE BETREFFENDER PROZESS STATTFINDET. UNTER W AHRSCHEINLICHKEIT, MIT DER EIN Die Bedeutung, welche die drei Effekte bei verschiedenen Photonen-Energien in unterschiedlichen Medien mit der Ordnungszahl Z haben, gibt die folgende Abbildung wieder: Abbildung 3-24 Seite 3-36 Photonenwechselwirkungen mit Materie bei unterschiedlichen Energien und Ordnungszahlen Kapitel 3 Naturwissenschaftliche Grundlagen Photoeffekt Beim Photoeffekt kommt es zu einer Wechselwirkung zwischen den Photonen (γ - Quanten) und den Elektronen der Atomhülle, derart, dass ein Elektron vollständig herausgeschlagen wird und gleichzeitig das γ-Quant verschwindet. Das freiwerdende Elektron wird Photoelektron genannt und erhält die Energie: EElektron = EPhoton - EBindung EElektron EPhoton EBindung = Energie des Photoelektrons = Energie des ursprünglichen Photons = Bindungsenergie des herausgeschlagenen Photoelektrons Beim Photoeffekt werden bevorzugt stark gebundene Elektronen aus den kernnahen Schalen (z.B. K-Schale) entfernt. Der Photoeffekt tritt vorzugsweise bei kleinen Quantenenergien EPhoton und großen Kernladungszahlen Z des Absorbermaterials auf. Der ergibt sich aus: σ Photo ~ σ Photo = Wirkungsquerschnitt Z5 E Photon 7 2 EPhoton = Photonenenergie Abbildung 3-25 Z= Kernladungszahl Der Photoeffekt COMPTONeffekt Beim COMPTONeffekt kommt es zu einer Wechselwirkung zwischen den Energiequanten und den Elektronen der äußeren Atomhülle, derart, dass ein Elektron (COMPTONelektron) abgetrennt wird, das γ-Quant aber mit verringerter Energie und veränderter Flugrichtung sich weiter bewegt. Seite 3-37 S. Prys / E. Foßhag Fachkunde im Strahlenschutz VERBUNDEN MIT DEM COMPTONEFFEKT IST ALSO IMMER EINE DEM URSPRÜNGLICHEN STRAHLENBÜNDEL HERAUS. STREUUNG DER PHOTONEN AUS Der COMPTONeffekt tritt auf bei mittleren Quantenenergien. Das gestreute γ-Quant kann weitere COMPTONeffekte hervorrufen bis seine Energie so niedrig geworden ist, dass es durch einen finalen Photoeffekt ganz aufgezehrt wird. Abbildung 3-26 Der Comptoneffekt Beim COMPTONeffekt überträgt das Photon dem Hüllenelektron die Energie: EElektron = EElektron EPhoton mec2 c Θ Y ⋅ EPhoton 1+ Y Y= EPhoton ⋅ (1 − cos Θ) mec 2 = Energie des COMPTONelektrons = Energie des γ-Quants = Ruhemasse des Elektrons = Vakuumlichtgeschwindigkeit = Streuwinkel des Photons DIE ENERGIEÜBERTRAGUNG BEIM COMPTONEFFEKT IST WEGEN DER STREUWINKELABHÄNGIGKEIT STARK DURCH DIE GEOMETRIE BEEINFLUSSBAR ! Seite 3-38 Kapitel 3 Naturwissenschaftliche Grundlagen Für cos Θ = 1 wird keine Energie übertragen, für cos Θ = 0 wird maximale Energie übertragen ! Der Wirkungsquerschnitt für den COMPTONeffekt ist: EPhoton << 2mec2 EPhoton >> 2mec2 σCompton ~ konstant σCompton ~ 1 / EPhoton Paarbildungseffekt Bei höheren Quantenenergien überwiegt in der Materie der Paarbildungseffekt. Dabei wird das Quant im elektrischen Feld des Kerns vernichtet und in ein Elektron-Positron-Paar umgewandelt. Das Quant muss mindestens eine Energie von 2me.c2 = 2 . 0,511 = 1,022 MeV aufweisen um diesen Effekt zu zeigen. Die über diesen Betrag hinausgehende Energie erscheint als kinetische Energie des Elektrons bzw. Positrons. EElektron + EPositron = EPhoton – 2mec2 EElektron = Energie des Photoelektrons EPositron = Energie des Photopositrons EPhoton = Energie des ursprünglichen Photons Sobald das Positron abgebremst ist, fängt es ein benachbartes Elektron ein und zerstrahlt. Dabei wird die bei der Entstehung verbrauchte Energie frei, indem 2 γ - Quanten mit je 511 keV abgestrahlt werden. Von Dichte und Geometrie des Absorbermaterials hängt es nun ab, ob keines, eines oder beide Quanten in Sekundärprozessen absorbiert werden. Entsprechend ist die insgesamt absorbierte Energie Eprimär - 1,022 MeV Eprimär - 0,511 MeV oder oder Eprimär. Der Paarbildungseffekt spielt vor allem bei Elementen mit großer Ordnungszahl eine Rolle. Oberhalb von 10 MeV wird der Hauptteil der Energie durch Paarbildung absorbiert. Der Wirkungsquerschnitt σPaar für den Paarbildungseffekt ergibt sich zu: σ Paar ~ Z 2 Seite 3-39 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Abbildung 3-27 Der Paarbildungseffekt Wechselwirkungen von Neutronen Die durch Kernspaltung oder Kernumwandlung erzeugten Neutronen haben Energien im MeVBereich. Sie können im Gegensatz zu Photonen nur mit anderen Atomkernen reagieren. Man teilt die möglichen Wechselwirkungsprozesse wie folgt ein: • elastische Stöße (Streuungen) zwischen Neutron und Atomkern Der Atomkern wird wie eine starre Kugel angestoßen und das Neutron aus seiner Bahn gelenkt. Dabei überträgt es einen Teil seiner Bewegungsenergie auf den Kern, den man auch entsprechend als Rückstoßkern bezeichnet. Der Energieverlust des Neutrons ist bei den leichten Kernen am größten; • inelastische Stöße (Streuungen) zwischen Neutron und Atomkern Bei inelastischen Stößen wird die vom Neutron übertragene Energie zum Teil zur Anregung des Atomkerns verbraucht, so dass der Energieverlust größer ist als bei elastischen Streuungen. Inelastische Streuungen kommen besonders häufig bei hohen Neutronenenergien und schweren Kernen vor; • Absorption mit Emission Das Neutron wird an den angeregten Atomkern angelagert (Einfangreaktion). Zur Stabilisierung wird entweder ein γ-Quant oder geladenes Teilchen emittiert. Aus dem Atomkern ist ein anderes Nuklid geworden; • Absorption mit Kernspaltung Bei besonders schweren Kernen, z.B. U-235 kommt es nach dem Einfang des Neutrons zur Kernspaltung; • Mehrteilchenprozesse und Spallationen Bei Wechselwirkungen von Atomkernen mit besonders hochenergetischen Teilchen können anschließend auch mehrere Nukleonen freigesetzt werden Mehrteilchenprozess), bzw. auch der Atomkern zersplittert werden (Spallation). Seite 3-40 Kapitel 3 Naturwissenschaftliche Grundlagen Die Abschirmung von Neutronenstrahlen ist wegen der vielfältigen Natur der Wechselwirkungen mit dem Absorbermaterial problematisch. Wirksame Neutronenabsorber sollten deshalb aus mehreren Schichten bestehen, nämlich aus Materialien mit Atomen hoher Ordnungszahl (Abbremsen durch inelastische Streuung), sowie aus Materialien mit niedriger Ordnungszahl, z.B. Wasserstoff (Abbremsen durch elastische Streuung) und schließlich aus Materialien mit hohem Einfangsquerschnitt für Neutronen (z. B. Cd, B). Die den Einfangprozess begleitende γ-Strahlung muss durch Materialien hoher Ordnungszahl (z.B. Pb) abgeschwächt werden. Entsprechende Schichten müssten also in der richtigen Reihenfolge zur Neutronenquelle angeordnet sein. In der Praxis verwendet man häufig homogene Mischungen dieser Abschirmmaterialien, die allerdings etwas schlechtere Abschirmeigenschaften aufweisen, dafür aber einfacher zu gestalten sind. Für den Schutz gegen Neutronen, die beispielsweise in Kernreaktoren entstehen, verwendet man deshalb auch Baryt- oder Normalbeton. 10 5 4 7 B + 01n → 11 5 B → 2 He + 3 Li Strahlendosen, Dosisgrößen und Dosiswirkungsbeziehungen Quelle H E D Aktivität E = Strahlungsenergie D = Energiedosis = dE / dm H = Personendosis [J] [ J / kg ] = [ Gy ] [ J / kg ] = [ Sv ] Abbildung 3-28 Strahlendosen Gesetzliche Grundlage für den Strahlenschutz gegen ionisierende Strahlen ist die Neufassung der Strahlenschutzverordnung (StrlSchV) vom 26.07.2001 (Bundesgesetzblatt, Teil 1 Nr. 38). Durch die im Folgenden beschriebenen Definitionen wird nicht die ionisierende Strahlung selbst, sondern lediglich die durch sie erzeugte Ladung, die auf die Materie übertragene Energie oder die hervorgerufene biologische Wirkung im Vergleich zu einer Bezugsstrahlung beschrieben. Je nach "Absorbermaterial" müssen deshalb andere Einheiten für die empfangene Strahlendosis verwendet werden: Strahlendosis in der Luft: Strahlendosis im Menschen: Strahlendosis vor Ort medizinische Bestrahlung: Strahlung in sonstiger Materie: Ionendosis Äquivalentdosis Äquivalentdosis Energiedosis Energiedosis [C/kg] früher Röntgen Sievert [Sv] = [J/kg] früher Rem [R] [rem] Gray [Gy] = [J/kg] [rd] früher Rad Seite 3-41 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Auf die Natur der Strahlung selbst sind Rückschlüsse nur bei genauer Kenntnis der Teilchenarten, ihrer Energien, sowie ihrer räumlichen Verteilung möglich ! Energiedosis D (absorbed dose) Absorbierte Strahlungsenergie pro Masse bestrahlten Stoffes 1 Gray = 1 Gy = 1 J / kg = 100 rad (radiation absorbed dose) Ionendosis I Erzeugte Ladung pro Masse durchstrahlter Luft (ρ = 1,293 g/l) Einheit: 1 C/kg Luft Früher: 1 Röntgen =1R = 2,58 x 10-4 As / kg Luft = 2,08 x 109 Ionenpaare / cm3 Luft = 3,33 x 10-10 As / cm3 Luft = 10-2 Ws / kg Luft Strahlenschutzgrössen (Körperdosisgrössen) Wenn ionisierende Strahlung auf lebende Materie trifft, sind im Gegensatz zu anderen Noxen einige Besonderheiten zu beachten: zum einen wird ein lebender Körper z.B. von Röntgen- oder GammaStrahlung durchdrungen, so dass radiochemische Prozesse direkt im Inneren der Zelle stattfinden können, während die meisten anderen Noxen häufig an der Zellmembran aufgehalten werden. Weiterhin erfolgt die Bestrahlung lebender Materie mit zeitlicher und räumlicher Diskontinuität, wobei die Ionisationsereignisse wie „Treffer“ entlang des Strahlenweges zu betrachten sind. Das Einschlagen eines Treffers in eine Zelle ist gleichzusetzen mit einer hohen Energiedisposition, die chemische Bindungsenergien um ein vielfaches übersteigt und deshalb strahlenchemische Reaktionen auslösen kann. Da die Treffer sehr unterschiedlich verteilt sein können und zudem auch noch stark von der Strahlenart abhängen können bei gegebener Strahlendosis die eintretenden Wirkungen erheblich differieren. Die Formulierung eines Dosisbegriffes in der Personendosimetrie gestaltet sich daher äußerst komplex. Die Mittelung von Energiedosen in Geweben bzw. Organen des Körpers bilden die Grundlage für die Definition sogenannter „Strahlenschutzgrössen“. Diese wurden eingeführt um stochastische Wirkungen bei niederen dosen zu begrenzen (siehe ICRP 103). Seite 3-42 Kapitel 3 Naturwissenschaftliche Grundlagen Organdosis (equivalent dose) Die Organdosis in einem Organ bzw. Gewebe HT ist definiert als: H T = ∑ wR ⋅ DT , R R HT = Organdosis im Gewebe T, T wR = Strahlungswichtungsfaktor für Strahlenart R DT,R = mittlere Energiedosis im Organ bzw. Gewebe T durch Strahlung R Die Einheit der Organdosis ist J/kg = Sievert (Sv).. Die Summierung wird über alle relevanten Strahlungsarten R durchgeführt. Die Strahlungswichtungsfaktoren wR sind mit geringfügigen ÄndeÄnd rungen aus ICRP 60 übernommen. Ursprung der wR-Faktoren Faktoren sind experimentelle Daten zur relatirelat ven biologischen Wirksamkeit (RBW) in ICRP 60 und ICRP 2003c. Strahlenart Photonen, alle Energien Elektronen und Myonen, alle Energien Protonen und geladene Pionen Alphateilchen, Spaltfragmente, schwere Kerne Neutronen Strahlenwichtungsfakt wR Strahlenwichtungsfaktor 1 1 2 20 Energieabhängig ! Tabelle 3-10 Strahlenwichtungsfaktoren für verschiedene dene Strahlenarten nach ICRP 103 Die Ermittlung der wR-Faktoren Faktoren für Neutronen wird nach ICRP 103 wie folgt empfohlen: 2,5 + 18,2 ⋅ e −[ln( En )] / 6 2 wR = 5,0 + 17,0 ⋅ e −[ln( 2 En )] / 6 2 2,5 + 3,2 ⋅ e −[ln( 0,04⋅En )] / 6 2 Abbildung 3-29 1MeV ≤ En ≤ 50 MeV En > 50 MeV En < 1MeV Die Zerstörungswirkung unterschiedlicher Strahlenarten bei gleicher Strahlendosis Seite 3-43 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Effektive Dosis HE (effective dose) Die effektive Dosis wird nach ICRP 60 definiert als H E = ∑ wT ⋅ H T T = ∑ wT ∑ wR ⋅ DT , R T R n Für den ganzen Körper ergibt sich der Wert 1 ∑wT =1 T =1 HE HT DT,R wT wR = effektive Dosis (HE wird in der StrlSchV mit E abgekürzt. Wegen der internationalen Konventionen wurde in diesem Kontext darauf verzichtet.); = Äquivalentdosen für spezielle Körperteile beim Menschen; = Organenergiedosis; = Gewebe-Gewichtungsfaktoren, die das stochastische Risiko berücksichtigen; = Strahlenwichtungsfaktor. Organ/Gewebe Keimdrüsen Knochenmark (rot) Dickdarm Lunge Magen Blase Brust Leber Speiseröhre Schilddrüse Haut Knochenoberfläche Andere Organe u. Gewebe1,2) Gewebe-Gewichtungsfaktor wT 0.20 0,12 0,12 0,12 0.12 0,05 0,05 0,05 0,05 0,05 0,01 0,01 0.05 Tabelle 3-11 Gewebe-Gewichtungsfaktoren für verschiedene Organe nach StrlSchV 1) Für Berechnungszwecke setzen sich andere Organe oder Gewebe wie folgt zusammen: Nebennieren, Gehirn, Dünndarm, Niere, Muskeln, Bauchspeicheldrüse, Milz, Thymusdrüse und Gebärmutter. 2) In den außergewöhnlichen Fällen, in denen ein einziges Organ oder Gewebe eine Äquivalentdosis erhält, die über die höchste Dosis in einem der 12 Organe oder Gewebe liegt, für die ein Wichtungsfaktor angegeben ist, sollte ein Wichtungsfaktor von 0,025 für dieses Organ oder Gewebe und ein Wichtungsfaktor von 0,025 für die mittlere Organdosis der restlichen Organe oder Gewebe gesetzt werden. Seite 3-44 Kapitel 3 Naturwissenschaftliche Grundlagen Die wT-Werte basieren auf epidemiologischen Studien über die Krebsentstehung bei verschiedenen Bevölkerungsgruppen. In ICRP 60 und ICRP 103 wird auf die Verfahren zur Summenbildung detaillierter eingegangen. Die effektive Dosis ist daher eine additive Größe. Operationelle Größen (Meßgrößen) Die oben beschriebenen Schutzgrößen zur Expositionsabschätzung sind nur berechenbar und praktisch nicht messbar. Sie präsentieren eine Äquivalentdosis, die für das weitere Verständnis und für entsprechende Messungen noch einer Präzisierung bedarf: Äquivalentdosis H (dose equivalent) Produkt aus D und Q in einem Punkt des Gewebes, wobei D die Energiedosis in ICRU Weichteilgewebe und Q der Qualitätsfaktor für die betrachtete Strahlung an diesem Punkt ist, also: H = Q⋅D H= Äquivalentdosis Q= Qualitätsfaktor D= Energiedosis Diese nur im Strahlenschutz angewandte Dosis wird als Äquivalentdosis H bezeichnet. Die Einheit der Äquivalentdosis H ist das Sievert: 1 Sievert = 1 Sv = 1 J / kg = 100 rem (roentgen equivalent man) Der Qualitätsfaktor Q (quality factor) Faktor, der die biologische Wirksamkeit einer Strahlung auf der Grundlage der Ionisationsdichte entlang den Spuren geladener Teilchen im Gewebe kennzeichnet. Q ist definiert als eine Funktion des unbeschränkten Linear-Energy-Transfers LET (L) geladener Teilchen in Wasser und ist energieabhängig. Die Qualitätsfaktoren sind besonders auf den Bereich von Havariedosen optimiert. Bei kleinen Dosen und bei Inkorporation radioaktiven Materials in den Körper gestaltet sich diese Dosimetrie zunehmend als problematisch. Erweiterte Dosisbegriffe nach ICRU und ICRP Es werden von der ICRU weitere, sogenannte operationelle, also messbare Größen eingeführt. Dieses sind Messgrößen für die Orts- und Personendosis-Überwachung bei äußerer Strahlungsexposition, die sich an einem Phantom, der sog. ICRU-Kugel ermitteln lassen. Seite 3-45 S. Prys / E. Foßhag Fachkunde im Strahlenschutz ICRU-Kugel: das ist ein kugelförmiges Phantom von 30 cm Durchmesser aus IRCU-Weichteilgewebe ( gewebeäquivalentes Material der Dichte 1g/cm3), Zusammensetzung 76,2 % Sauerstoff, 11,1% Kohlenstoff, 10,1% Wasserstoff und 2,6% Stickstoff. Ortsdosis: Umgebungs-Äquivalentdosis H*(10) (ambient dose equivalent) Äquivalentdosis an einem Punkt im Strahlungsfeld, die im zugehörigen aufgeweiteten und ausgerichteten Strahlungsfeld auf dem der Einfallsrichtung der Strahlung entgegengesetzten Radiusvektor der ICRU-Kugel in 10 mm Tiefe erzeugt würde. Die Einheit der Umgebungs-Äquivalentdosis ist das Joule durch Kilogramm (J /kg = Sievert (Sv). Ortsdosis: Richtungsäquivalentdosis H‘(0,07,Ω) (directional dose equivalent) Äquivalentdosis an einem Punkt im Strahlungsfeld, die im zugehörigen aufgeweiteten Strahlungsfeld auf einem in festgelegter Richtung Ω orientierten Radius der ICRU-Kugel in der Tiefe 0,07 erzeugt würde. Die Einheit der Richtungs-Äquivalentdosis ist das Joule durch Kilogramm (J /kg = Sievert (Sv). Tiefen-Personendosis: Hp(10) (personal dose equivalent) Eine Dosismessgröße für die Äquivalentdosis in ICRU-Weichteilgewebe in einer geeigneten Tiefe d=10 mm unter der Stelle der Körperoberfläche, an der das Personendosimeter getragen wird. Dieser Wert wird zur Schätzung der effektiven Dosis gewählt. Die Einheit ist das Joule durch Kilogramm (J /kg = Sievert (Sv). Oberflächen-Personendosis: Hp(0,07) Diese Dosismessgröße wird zur Schätzung der Haut-, Hand- und Fußdosis verwendet und entspricht der Dosis in einer Tiefe von 0,07 mm. Seite 3-46 Kapitel 3 Naturwissenschaftliche Grundlagen Zusammenfassung Schutzgrößen und operative Größen Abbildung 3-30 Einteilung der operativen Größen Die operativen Größen sind messbar. Unter der Ortsdosis versteht man die Äquivalentdosis, Äquivalen gemessen an einem bestimmten Ort. Als Ortsdosis gilt bei durchdringender Strahlung die Umgebungs-Äquivalentdosis Äquivalentdosis H*(10). H*(10). Als Ortsdosis gilt bei Strahlung mit geringer Eindringtiefe die Richtungs-Äquivalentdosis Äquivalentdosis H*(0,07,Ω H*(0,07,Ω). Sie sollen unter möglichstt realistischen ExpositionsbeExpositionsb dingungen ausreichend genaue Schätzwerte für die Körperdosen liefern. Unter der Personendosis versteht man die Äquivalentdosis gemessen an der für die Strahlenexposition repräsentativen Stelle der Körperoberfläche. Sie liefert die Schätzwerte für die Körperdosis. Der Messwert für die TiefenTiefen Personendosis Hp(10) liefert bei Ganzkörperexposition mit durchdringender Strahlung einen Schätzwert für die effektive Dosis und die Organdosen. Der Messwert für die OberflächenOberflächen Personendosis Hp(0,07) liefert bei Teilkörperexposition mit Strahlung geringer Eindringtiefe einen Schätzwert für die lokale Hautdosis. Diese Angaben beziehen sich auf die ICRU-Kugel. ICRU Die Schutzgrößen (Körperdosisgrößen) (Körperdosisgrö können nur über Rechnungen oder Messungen an Phantomen ermittelt werden. Wird bei den Messungen der operativen Größen der Wert von 5 mSv überschritten sind die Körperdosen nach entsprechendem Berechungsverfahren zu ermitteln. Die Abschätzung der Strahlenexposition Strahle Die Dosisabschätzung bei Exposition von äußeren Quellen erfolgt durch persönliche Überwachung mit Personendosimetern, die am Körper getragen werden, bzw. bei potenziellen Expositionen durch Messung oder Schätzung von H*(10) und Anwendung geeigneter geeigneter Konversionskoeffizienten. Die Messgrößen in der Personendosimetrie sind Hp(10) und Hp(0,07). Wenn das Personendosimeter an einem Ort am Körper getragen wird, der für die Strahlenexposition repräsentativ ist, dann liefert der Wert von Hp(10) bei niedriger riger Dosis und homogener Ganzkörperexposition einen für StrahlenStrahle schutzzwecke ausreichend genauen Wert für die effektive Dosis. Seite 3-47 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Die Abschätzung der Exposition bei innerer Strahlenexposition durch Inkorporation von Radionukliden basiert auf Rechnungen zur Zufuhr des Radionuklids. Die Zufuhr kann entweder durch direkte Messungen (externe Überwachung des Körpers oder gezielter Organe) oder durch indirekte Messungen (Urin- und Stuhlproben) oder durch Messung an Umweltproben abgeschätzt werden im Zusammenhang mit biokinetischen Modellen. Die effektive Dosis wird dann aus der Zufuhr unter Verwendung von Dosiskoeffizienten ermittelt, die auf ICRU-Empfehlungen basieren. In Analogie zu toxikologischen Prinzipien muss bei Inkorporationen das Konzentrations-Zeit-Produkt (CTProdukt) am Wirkungsort berücksichtigt werden. Beispiel 1: Bei einer Inkorporation von Cs-137 - Salz muss berücksichtigt werden, da es sich meist um gut lösliche Substanzen handelt, die sich ziemlich gleichmäßig im Körper verteilen, also eine Art Ganzkörper-Beta-Bestrahlung darstellen. Beispiel 2: Bei einer Inhalation von Pu-239 - Staub (PuO2) kann sich das Radionuklid kaum im Körper verteilen, da die Substanz weitgehend wasserunlöslich ist, vielmehr entsteht eine lokale Anreicherung des Alpha-Strahlers in der Lunge (hot-spot). Dosiswirkungsbeziehungen Stochastische und nicht-stochastische Strahlenwirkungen Die biologischen Strahlenwirkungen stellen ein äußerst komplexes Geschehen dar, das von sehr unterschiedlichen Einflussgrößen abhängt ( Siehe hierzu Kapitel Biologische Strahlenwirkungen). Die Strahlenwirkungen auf den Menschen werden ganz allgemein eingeteilt in 2 Gruppen. Bei der ersten Gruppe handelt es sich um solche Strahlenschäden, die bei einer Strahlenexposition nach Überschreiten gewisser Schwellen-Dosiswerte mit großer Sicherheit auftreten, sogenannte nichtstochastische oder deterministische Wirkungen, wie z.B. Hautrötung, charakteristische Veränderungen des Blutbildes, Störungen der Fertilität oder Trübungen der Augenlinsen (Kataraktbildung). Demgegenüber steht die zweite Gruppe der sogenannten stochastischen Wirkungen, wo die Wahrscheinlichkeit eines Schadens ungeachtet des Schweregrades deutlich in Abhängigkeit von der Strahlendosis zu beobachten ist. Dazu gehören Erkrankungen an malignen Tumoren (wie z.B. Leukämie oder Krebs) oder auch andersartige genetische Mutationen. Es wird angenommen, dass es für diese Gruppe radiogener Schäden keine Schwellendosis gibt. Seite 3-48 Kapitel 3 Naturwissenschaftliche Grundlagen Abbildung 3-31 Dosis-Wirkung-Kurve Dosisleistung und Geometrieeinflüsse Die Dosisleistung ist ein Maß für die pro Zeiteinheit empfangene Dosis. Sie wird für verschiedene Strahlenarten unterschiedlich rechnerisch ermittelt und hängt stark von der Geometrie des Strahlers ab. Die Dosisleistungseinheiten gseinheiten sind: Gy /s, Gy /a, Sv /h, W / kg usw. Die Dosisleistung ist die zeitliche Ableitung der Dosis: • D= • dD dt H= dH dt Die Dosisleistung hängt stark von der Strahlenart und der Geometrie des Strahlers ab. Sehr häufig wird im praktischenn Strahlenschutz eine Näherung als punktförmige Quelle angenommen. Das ist aber nicht immer gerechtfertigt ! Dosisleistung bei punktförmige Strahlenquellen: • A r2 Für γ-Strahlen gilt: H = ΓH ⋅ für β-Strahlen gilt: H = Β H (r , ρ , E max ) ⋅ ΓH A r • = γ - Dosisleistungskonstante (tabelliert) = Aktivität des Strahlers = Abstand vom Strahler A r2 ΒH ρ Emax = β - Dosisleistungsfunktion = Dichte des umgebenden Mediums = maximale Beta-Energie Seite 3-49 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Dosisleistung bei kreisscheibenförmigen Strahlenquellen: • A ⋅ f γ ( R, r ) r2 Für γ-Strahlen gilt: H = ΓH ⋅ für β-Strahlen gilt: H = Β H (r , ρ , E max , F ) ⋅ fγ (R,r) R • A F = Geometriefunktionen (tabelliert) = Radius der Kreisscheibe F = Fläche des Strahlers für Kreis: F = π.R2 Abbildung 3-32 Geometrieeinflüsse bei Strahlendosen Strahlung im Alltag Die natürliche Strahlenbelastung ist abhängig von Höhe und Zusammensetzung des Erdbodens an der Stelle, wo ein Mensch lebt. In der unten angegebenen Tabelle werden die wichtigsten Pfade für die natürliche Strahlenbelastung aufgezeigt und den zivilisatorisch bedingten Expositionen gegenübergestellt. (Mittlere effektive Dosis der Bevölkerung in der BRD 1988 in mSv) Natürliche Strahlenexposition Summe 2,4 kosmische Strahlung 0,3 terrestrische Strahlung 0,5 Radon-Inhalation 1,3 Inkorporationen 0,3 Zivilisatorische Strahlenexposition Summe ca. 1,6 kerntechnische Anlagen < 0,01 med. Diagnostik 1,5 Industrieerzeugnisse < 0,01 berufliche Strahlenexposition < 0,01 technische Strahlungsquellen < 0,01 Fallout Kernwaffenversuche < 0,01 Tschernobyl 0,04 Tabelle 3-12 Natürliche und zivilisatorische Strahlenbelastung des Menschen Seite 3-50 Kapitel 3 Naturwissenschaftliche Grundlagen DIE MITTLERE NATÜRLICHE STRAHLENBELASTUNG IN DEUTSCHLAND BETRÄGT CA. 2,4 mSV/ a (=0,27 µSv/h). DIESE ERHÖHT SICH UM EINE ZIVILISATORISCH BEDINGTE BELASTUNG AUF CA. 4 mSV/ a. Besondere Regionen der Erde mit erhöhter terrestrischer Strahlenbelastung sind: Frankreich (Granitbezirke) Indien (Kerala-Küste) Brasilien (Atlantikküste) Iran (Stadt Ramsar) 2, 5 - 4 10 - 40 8 - 200 18 - 450 mSv / a mSv / a mSv / a mSv / a Tabelle 3-13 Regionen erhöhter natürlicher Radioaktivität Signifikante Dosisleistungswerte sind: 3 h Flug pro Jahr in 10 km Höhe Zusätzliche Strahlenbelastung beim Wohnen in Beton oder Granit Dosisgrenzwert für beruflich strahlenexponierte Personen Natürliche Strahlenbelastung im Monazit (Brasilien) 0,01 mSv/a 3 mSv/a 20 mSv/a 200 mSv/a Tabelle 3-14 Signifikante Dosisleistungswerte Signifikante Dosiswerte bei einmaliger Ganzkörperbestrahlung und fehlender ärztlicher Behandlung sind: Tödliche Dosis Schwere Strahlenkrankheit Vorübergehende Strahlenkrankheit (Strahlenkater) Erste klinisch erfassbare Strahleneffekte 7000 mSv 4000 mSv 1000 mSv 250 mSv Tabelle 3-15 Signifikante Dosiswerte bei einmaliger Ganzkörperbestrahlung und fehlender ärztlicher Behandlung Seite 3-51 S. Prys / E. Foßhag Fachkunde im Strahlenschutz Beispiele für Radionuklidanwendungen in der Nuklearmedizin In der Nuklearmedizin werden offene radioaktive Stoffe zu diagnostischen und therapeutischen Zwecken eingesetzt. In der Diagnostik werden Radionuklide zur Markierung bestimmter Verbindungen im Stoffwechsel verwendet um Verteilung, Anreicherung oder Ausscheidung mittels geeigneter Detektoren zu bestimmen, sowie auch Radioimmunoassays (Antikörper / Antigenbestimmungen mittels radioaktiver Indikatoren). Die Auswertung dieser Messdaten ermöglicht Aussagen zur Funktion betreffender Organe. Die verwendeten Radionuklide werden in Isotopengeneratoren, Teilchenbeschleunigern oder auch in Kernreaktoren hergestellt. Typischer Weise werden in der Nuklearmedizin die in der Tabelle angegebenen Radionuklide verwendet. Radionuklid C-11 Halbwertszeit 20 min 27,8 d 45,1 d 270 d 5,26 a Strahlung β+, γ (511keV) ε, β+, γ (511keV) ε, γ β -, γ ε, γ β -, γ F-18 110 min Cr-51 Fe-59 Co-57 Co-60 Diagnostik Diagnostik Diagnostik Therapie Se-75 120 d ε, γ Diagnostik Tc-99m 6 h γ, I Diagnostik In-111 I-123 2,8 d 13,3 h ε, γ ε, γ Diagnostik Diagnostik I-131 8,1 d β -, γ (Diagnostik) Therapie Xe-133 Au-198 5,3 d 2,7 d β-, γ, eβ -, γ Ir-192 Tl-201 74,2 d 73 h β -, γ ε, γ Diagnostik Diagnostik Therapie Therapie Diagnostik Tabelle 3-16 − β β+ γ ε Seite 3-52 Diagnostik Diagnostik Anwendung Positronenemissionstomographie, PET Organfunktionen, Krebserkennung Positronenemissionstomographie, PET Organfunktionen, Krebserkennung Markierung / Hämatologie Markierung / Ferrokinetik Markierung / Vitamin B-12 Krebsbehandlung, wird zunehmend ersetzt durch Linearbeschleuniger Markierung / Bauchspeicheldrüsenszintigraphie Markierung / umfangreiche Anwendung z.B. in der Schilddrüsenszintigraphie, Leberszintigraphie, Knochenszintigraphie Markierung / Stoffwechsel Schilddrüsenszintigraphie, Markierung, SPECT Gehirnabbildungen Schildrüsentherapie, Krebstherapie der Schilddrüse, z.T. auch noch in der Schilddrüsendiagnostik (veraltert) Lungenventilation und Perfussion Leberszintigraphie Krebstheraphie Kardiologie Medizinische Anwendungen von Radionukliden e- = Negatronen (Beta)-Zerfall = Positronen (Beta)-Zerfall = Gamma-Zerfall = Elektroneneinfang, Umwandlung durch Einfang eines Hüllenelektrons, Aussendung von Röntgenstrahlung = Konversionselektronen I = isomerer Übergang, Kapitel 3 Naturwissenschaftliche Grundlagen Übungsfragen 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. Was sind Nukleonen, welche gibt es ? Was ist die Ursache für den radioaktiven Zerfall ? Welcher Gesetzmäßigkeit unterliegt der radioaktive Zerfall ? Was versteht man unter isomeren Nukliden ? Nennen Sie die drei Isotope des Wasserstoffs ? Welche radioaktiven Zerfallsreihen kennen Sie ? Wie ist die (mittlere) Lebensdauer eines Radionuklids definiert ? Was versteht man unter Spallation ? Erläutern Sie den Unterschied zwischen Auger-Elektronen und Konversionselektronen ! Erläutern Sie den Unterschied zwischen Röntgen- und Gamma-Strahlung ! Wie lassen sich die verschiedenen Arten ionisierender Strahlung abschirmen ? Welche Einheit gibt man bei Oberflächenkontaminationen an ? Was versteht man unter der Ortsdosis ? Was versteht man unter Personendosis ? Was versteht man unter der Umgebungs-Äquivalentdosis ? Was versteht man unter der Tiefen-Personendosis ? Welche wichtigen Einheiten kennen Sie für Dosisangaben ? Was versteht man unter dem Kerma ? Wie berechnet sich die γ - Äquivalentdosisleitung eines kreisscheibenförmigen Strahlers ? Was passiert, wenn γ-Strahlung auf Materie trifft ? Bei welchem Streuwinkel wird beim Comptoneffekt die maximale Energie übertragen ? Erläutern Sie den Paarbildungseffekt ! Wann tritt er ein ? Was versteht man unter der relativen biologischen Wirksamkeit ? Wie groß ist die mittlere zivilisatorisch bedingte Strahlenbelastung in Deutschland ? Was sind stochastische Strahlenwirkungen ? Was versteht man unter der Strahlenhormesis ? Recherchieren Sie ! Literatur: 1. 2. 3. 4. 5. 6. 7. 8. K.H. Lieser; Einführung in die Kernchemie; VCH Verlag; 1990 M. Volkmer; Radioaktivität und Strahlenschutz; Informationskreis Kernenergie, Überarb. Auflage 2007 M. Volkmer; Kernenergie Basiswissen; Informationskreis Kernenergie, Überarb. Auflage 2007 H-G. Vogt; Grundzüge des praktischen Strahlenschutzes; Carl Hanser Verlag, 5. Aufl. 2010 W. Kölzer; Lexikon zur Kernenergie; aktualisierte Fassung Jan. 2010; ISBN 3-923704-32-1 W. Stolz; Radioaktivität: Grundlagen-Messung-Anwendungen; Teubner Verlag, 5. Überarb. Aufl. 2005 TOICD, Nuklidkarte auf CD von Wiley-Interscience (8. Auflage, Version 1, März 1996) C. Grupen; Grundkurs im Strahlenschutz, Praxiswissen für den Umgang mit radioaktiven Stoffen, Springer Verlag 2008 Dazu im Internet http://www.bfs.de/ http://www.ptb.de/ http://www.fs-ev.de/ http://www.kernenergie.de/ Seite 3-53