Protokoll Versuch E 111 Jamininterferometer

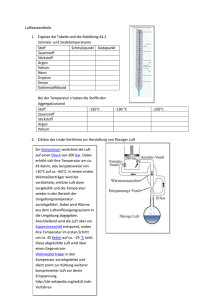
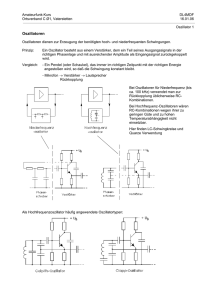
Physikalisches Fortgeschrittenenpraktikum
der Universität Bonn
Sommersemester 2003
Protokoll
Versuch E 111
Jamininterferometer
Dirk Bringer (Physik)
Lars Lemsch (Chemie)
Iris Xhango (Physik)
24. Februar 2003
1
Versuch E 111 - Jamininterferometer
1.
1.
2.
3.
Inhaltsverzeichnis
Inhaltsverzeichnis
Zielsetzung des Versuches
Theoretische Grundlagen
3.1
Herleitung einer Bestimmungsgleichung für die Dispersion
3.2
Korrektur auf Normalbedingungen
3.3
Das Auswertungsverfahren
4. Versuchsaufbau und Durchführung
4.1
Versuchsaufbau
4.1.1
Das Jamininterferometer
4.2
Versuchsdurchführung
4.2.1
Justierung des optischen Systems
4.2.2
Experimentelle Durchführung
5. Messergebnisse und Auswertung
5.1
Die Zählung der m-Interferenzmaxima
5.2
Auswertung
5.2.1
Berechnung von (n-1)
5.2.2
Graphische Darstellung der Messergebnisse und lineare Regression
5.2.2.1 Bestimmung der Oszillatorstärke fo
5.2.2.2 Bestimmung der Resonanzfrequenz ν0
5.2.2.3 Berechnung der statischen Dielektrizitätskonstante ε0
6. Fehlerdiskussion
6.1
Bewertung
7. Literatur
2
3
3
3
5
5
6
6
6
7
7
7
8
8
9
9
11
11
12
12
13
13
14
2
Versuch E 111 - Jamininterferometer
2.
Zielsetzung des Versuches
In diesem Versuch soll mit Hilfe eines Jamin-Interferometers die Dispersionskurve, d.h. die Abhängigkeit
des Brechungsindex n von der Wellenlänge der Strahlung, des Edelgases Argon im sichtbaren
Wellenlängenbereich vermessen werden. Aus den experimentellen Ergebnissen wird dann über die
Dispersionsrelation die erste Resonanzfrequenz ν0, die Oszillatorstärke f0 und die statische
Dielektrizitätskonstante ε0 bestimmt.
3.
Theoretische Grundlagen
3.1
Herleitung einer Bestimmungsgleichung für die Dispersion
Die Abhängigkeit der Brechzahl eines Dielektrikums von der eingestrahlten Wellenlänge wird als Dispersion
bezeichnet. Eine theoretische Behandlung dieses Phänomens geht von der Wechselwirkung
elektromagnetischer Strahlung mit den Elektronen des Mediums, in diesem Falle Argon, aus. Für die
Entwicklung der Modellvorstellung gehen wir von folgenden Annahmen aus:
1.
2.
Es handelt sich um isotrope Dielektrika, d.h. die untersuchte Substanz weist kein permanentes
Dipolmoment auf.
Die Elektronen führen eine gedämpfte harmonische Schwingung um ihr Ruhepotential aus.
Das Potential der Elektronen im Coulombfeld des Kerns und lässt sich in der Nähe der Ruhelage als
Parabel(Oszillator-)Potential approximieren. Wird nun ein äußeres elektromagnetisches Wechselfeld
eingestrahlt, so wirkt eine Kraft auf das Elektron, die Lorentz-Kraft:
(
)
r
r 1 r r 
F = −e  E + v × B 
c


(1)
r
r
Bei dieser Betrachtung im CGS-System liegen E und B in der gleichen Größenordnung. Da die
r
Geschwindigkeit v des Elektrons wesentlich kleiner ist als die Lichtgeschwindigkeit c, können wir das
magnetische Glied in (1) vernachlässigen. Auf das Elektron wirkt also vereinfacht die Kraft
r
r
F = −eE
(2)
Die Bewegung des Elektrons lässt sich mit den genannten Näherungen als erzwungene gedämpfte
harmonische Schwingung beschreiben. Die aus der klassischen Mechanik bekannte Differentialgleichung
lautet:
r
m&r& = −γr& − mw02 r − eE
(3)
bzw.
&r& = −
γ
m
r& − w02 r −
e r
E
m
(3)
Dabei ist w0 die Eigenfrequenz und γ die Dämpfungskonstante der Schwingung.
r r
Mit r ∝ E ∝ e −iωt erhält man die Lösung:
r
r
e
1
r (t ) = −
E (t )
2
2
m ω 0 − ω − iγω
(
)
(4)
3
Versuch E 111 - Jamininterferometer
Nach Annahme 1 besitzt das betrachtete Atom kein Dipolmoment. Wir können daher das durch das
elektromagnetische Wechselfeld induzierte Dipolmoment berechnen. Für das i-te Elektron ergibt sich:
r
r
r e2
1
pi = −e ⋅ ri =
E atom (t )
2
2
m ω 0 − ω − iγω
(
)
(5)
Betrachtet man nicht nur ein Elektron, sondern die verschiedenen Elektronen des Atoms mit den
Eigenfrequenzen ω n der verschiedenen Schalen, so resultiert bei einer Teilchendichte von N Atomen je cm3
die Gesamtpolarisation P
r Ne 2
P=
m
∑ (ω
n
fn
− ω − iγω
2
n
2
)
r
E atom (t )
(6)
Damit ist ein Zusammenhang zwischen dem elektrischen Feld am Ort der Elektronen und der Polarisation
r
hergestellt. Die Beziehung zwischen E atom und der makroskopischen Feldstärke E kann nach Lorentz
genähert werden als
r
r 4π r
E atom = E +
P
3
(7)
Außerdem gilt für die Verschiebungsdichte D
r
r r
r
D = εE = E + 4πP
(8)
Damit können wir folgenden Ausdruck für das elektrische Feld am Ort der Elektronen herleiten:
r
4π ε + 2 r
E atom =
P
3 ε −1
(9)
Umstellen von Gleichung (9) und anschließendes ersetzen von P durch den Ausdruck in Gl. (6) ergibt:
ε − 1 4π Ne 2
=
ε +2
3 m
∑ (ω
n
fn
2
n
− ω 2 − iγω
(10)
)
Führen wir nun den Brechungsindex n über die Maxwellsche Relation n = ε ein, so erhalten wir den
folgenden auch als Lorenz-Lorenzsche Gleichung bezeichneten Zusammenhang:
n 2 − 1 4π Ne 2
=
3 m
n2 + 2
∑ (ω
n
fn
2
n
− ω 2 − iγω
)
(11)
Zur Anwendung der Relation in unserem Versuch werden einige Näherungen gemacht:
1.
2.
3.
Der Dämpfungsterm −iγω wird vernachlässigt. Dies ist vertretbar, da die Messungen in
Frequenzbereichen durchgeführt werden, die weit unterhalb der ersten Resonanz der Argon-Atome
liegen.
Die weiteren Resonanzfrequenzen liegen sehr weit von der ersten entfernt. Wir berücksichtigen
daher nur das erste Glied der Summation.
Der Brechungsindex des Gases Argon ist ungefähr 1.
Als Folge von Annahme 3 ergibt sich:
n 2 − 1 (n + 1)(n − 1) 2
≈
≈ (n − 1)
3
3
n2 + 2
(12)
Wir erhalten also folgende Bestimmungsgleichung
4
Versuch E 111 - Jamininterferometer
n −1 =
f0
Ne 2
2
2πm ν 0 − ν 2
(
)
(13)
mit der Oszillatorstärke f0 und der Resonanzfrequenz ν0.
3.2
Korrektur auf Normalbedingungen
Aus Gleichung (13) ist ersichtlich, dass der Brechungsindex n von der Teilchendichte N abhängt. Um
eventuell schwankende Druck und Temperaturbedingungen während des Versuches auszugleichen und die
Vergleichbarkeit mit Literaturwerten sicherzustellen, werden die gemessenen Werte auf Normalbedingungen
normiert. Sieht man Argon unter Raumbedingungen als ideales Gas an, so kann die Korrektur der
Messergebnisse mit Hilfe der idealen Gasgleichung erfolgen.
p = NkT
(14)
Als Korrekturfaktor ergibt sich:
K=
3.3
N0
pT
= 0
N
pT0
(15)
Das Auswertungsverfahren
Die interferometrischen Messungen liefern den Brechungsindex für verschiedene eingestrahlte Wellenlängen.
Über eine graphische Auswertung sollen aus dieser Datenmenge die Größen f0, ν0 und die statische
Dielektrizitätskonstante ε0 bestimmt werden. Dazu wird (n-1)-1 gegen ν2 aufgetragen. Nach gewichteter
linearer Regression können die gesuchten Werte aus Steigung und Achsenabschnitt bestimmt werden.
Die Geradengleichung lautet:
(n − 1)−1 = aν 2 + b
(16)
Im SI-System erhalten wir:
8π 2 ε 0 m ν 02 − ν 2
1
=
n −1
f0
Ne 2
a=−
8π 2 ε 0 m
Ne 2 f 0
b = −aν 02
(17)
(18)
(19)
5
Versuch E 111 - Jamininterferometer
4.
Versuchsaufbau und Durchführung
4.1
Versuchsaufbau
Abbildung 1 - Schematischer Aufbau der Versuchsapparatur
Das Licht einer durch einen Holzkasten abgeschirmten Quecksilber (Hg)- bzw. Cadmium (Cd)- Dampflampe
trifft durch einen Spalt auf ein Pellin-Broca-Prisma. Dieses dient zur Spektralzerlegung und zur Selektion der
Spektrallinien. Die Besonderheit dieses Prismas liegt darin, dass unter einem bestimmten Winkel einfallendes
Licht einer bestimmten Wellenlänge genau um 90° gebrochen wird. Dies ermöglicht eine einfache Selektion
von Spektrallinien durch Drehung des Prismas, ohne dass die gesamte Apparatur verändert werden muss. Die
anderen Spektrallinien werden im weiteren Verlauf des Lichtstrahls mit einem zweiten Spalt ausgeblendet.
Der selektierte monochromatische Lichtstrahl kann mit einer Linse fokussiert werden. Dabei sollte der
Schärfebereich in die Mitte der Argonkammern gelegt werden, um unerwünschte Interferenzen durch
Reflektionen an den Kammerwänden auszuschließen. Der Strahl gelangt dann in ein Jamininterferometer.
4.1.1
Das Jamininterferometer
Das Interferometer besteht aus zwei zueinander annähernd parallelen Glasplatten, G1 und G2, der Dicke d, die
rückseitig verspiegelt sind. Zwischen den beiden Glasplatten befinden sich zwei getrennte Kammern, die an
den Schmalseiten durchstrahlt werden können. Der einfallende Lichtstrahl trifft im 45°-Winkel auf die erste
Glasplatte, wird zu etwa 5% an der Oberfläche von G1 reflektiert und durchläuft die erste Argonkammer
(Strahl 1). Der durchgelassene und gebrochene Strahl wird an der verspiegelten Rückseite reflektiert, zu etwa
95% an der Oberfläche transmittiert und gelangt anschließend in die zweite Argonkammer (Strahl 2). Der an
der Oberfläche reflektierte Anteil gelangt nicht in die Kammer, da diese entsprechend abgeklebt wurde. Nach
dem Durchlaufen der Argonkammern treffen die Lichtstrahlen auf eine zweite Glasplatte. Der anfangs
reflektierte Lichtstrahl 1, wird teilweise an der Oberfläche von G2 reflektiert (5 % der Intensität). Der nicht
reflektierte Anteil läuft durch das Glas, wird an der verspiegelten Rückseite reflektiert und tritt an der
Oberfläche wieder aus. Die beim Eintritt in die Glasplatte reflektierten Anteile werden über eine Blende
eliminiert. Strahl 2 wird an der Oberfläche von G2 zu 5% reflektiert und zwar genau an der Stelle an der
Strahl 1 austritt. Die Anteile des Strahl, die durch das Glas laufen und weitere Reflektionen erfahren werden
ebenfalls ausgeblendet. Die beiden sich überlagernden Strahlen gleicher Intensität können mit einem auf
unendlich gestellten Fernglas beobachtet werden und zeigen ein Streifenmuster aus hellen und dunklen
Bereichen. Diese Interferenz beruht darauf, dass die beiden verspiegelten Glasplatten nicht völlig parallel
ausgerichtet, sondern leicht gegeneinander verkippt sind. Dadurch wird bereits ohne Befüllung der
Argonkammern ein Gangunterschied zwischen den beiden betrachteten Teilstrahlen erzeugt.
6
Versuch E 111 - Jamininterferometer
4.2
Versuchsdurchführung
4.2.1
Justierung des optischen Systems
Bei Inbetriebnahme des Versuchsaufbaus konnten keine Intereferenzerscheinungen beobachtet werden.
Daher musste das gesamte optische System neu justiert werden. Zu diesem Zweck verwendeten wir die gut
sichtbare grüne Spektrallinie der Hg-Lampe, die über das Pellin-Broca-Prisma und den Spalt selektiert
wurde. Nach Ausbau des Kammersystems wurde der Lichtstrahl auf einem Blatt Papier als Mattscheibe in
der Mitte des Jamininterferometers fokussiert. Danach konnten die Kammern wieder eingebaut werden.
Diese wurden dann so eingerichtet, dass nur die zwei zu betrachtenden Strahlen durch die Kammern liefen.
Es wurde dabei darauf geachtet, möglichst keine Reflexionen innerhalb des Kammersystems zu verursachen.
Nach Abschluß der Einrichtung konnten Interferenzerscheinungen durch das Fernrohr beobachtet werden.
Reflektierte Anteile der an G2 austretenden Strahlen wurden mittels einer weiteren Blende vor dem Fernrohr
eliminiert. Zum Schluß wurde bei Beobachtung der Interferenzstreifen durch das Fernglas noch die Lampe so
ausgerichtet, dass eine optimale Beleuchtung des Spaltes gewährleistet wurde.
4.2.2
Experimentelle Durchführung
Abbildung 2 - Schematische Darstellung des Gassystems
Über das in Abbildung 2 schematisch dargestellte Gassystem wurden die beiden Kammern 5 Minuten bei
geöffnetem System mit Argon (Durchfluss 5 l/min) gespült, so dass schließlich das gesamte Kammersystem
mit Argon unter Atmosphärendruck gefüllt war. Der Ausgangsdruck im Inneren des Systems konnte so über
den Umgebungsdruck, der am Wandbarometer abgelesen wurde, bestimmt werden. Nach dem Schließen der
Ventile, wobei unter anderem die Verbindung zwischen den beiden Kammern unterbrochen wurde, wurde
eine der Kammern mit Hilfe einer Vakuumpumpe evakuiert. Durch diese langsame Evakuierung ändert sich
die Teilchendichte in dieser Argonkammer und damit die optische Weglänge und der Brechungsindex. Durch
die Änderung der optischen Weglängendifferenzen zwischen den Strahlen 1 und 2 während des Abpumpens
wanderten die im Fernrohr beobachteten Interferenzmaxima nach oben. Die Zahl der bis zur vollständigen
Evakuierung (p= 0,15 mbar) vorbeigewanderten Interferenzmaxima wurde gezählt und aus diesem Wert der
Brechungsindex berechnet (siehe Auswertung). Die Evakuierung der Kammer auf einen Druck von 0,15
mbar schien ausreichend zu sein, da sich in diesem Druckbereich das Interferenzmuster nicht mehr verschob.
Die Messung wurde für sechs verschiedene Spektrallinien der Hg- und Cd-Lampe durchgeführt. Vor jeder
Messung wurden die Temperatur an der Kammer und der Außendruck abgelesen. Nach jeder Messung
wurden beide Kammern wieder befüllt, kurz mit Argon gespült und auf Ausgangsbedingungen gebracht.
7
Versuch E 111 - Jamininterferometer
5.
Messergebnisse und Auswertung
5.1
Die Zählung der m-Interferenzmaxima
Zunächst wurden die ausgewählten Spektrallinien der Hg-, dann die der Cd-Dampflampe verwendet. Die
Anzahl der bei der Evakuierung vorbeigewanderten Interferenzmaxima bei der verwendeten Spektrallinie
sind zusammen mit den Randbedingungen (Temperatur, Druck) in folgender Tabelle zusammengefasst:
Wellenlänge
λ
Frequenz
ν [Hz]
ν2 [Hz2]
Streifen
-zahl, m
∆m
p
[mbar]
T [°C]
1020
20,22
293,37
1020
20,40
293,55
1020
19,72
292,87
1020
19,88
293,03
1020
18,02
291,17
1020
18,04
291,19
175
1020
20,75
293,90
180
1020
20,50
293,65
1020
20,60
293,75
1020
20,48
293,63
1020
20,60
293,75
211
1020
20,71
293,86
221
1020
20,02
293,17
1020
20,10
293,25
1020
20,10
293,25
138
Cd rot
643,85 nm
4,6562·10-7
2,1681·10-29
144
6
162
Hg gelb
576,96 nm
5,1961·10-7
2,6999·10-29
164
6
180
Hg grün
546,07 nm
Cd grün
508,58 nm
5,4900·10-7
5,8947·10-7
3,0140·10-29
3,4747·10-29
165
184
4
6
193
Cd blau
467,88 nm
Hg indigo
435,83 nm
6,4075·10-7
6,8787·10-7
4,1056·10-29
4,7316·10-29
207
213
202
8
15
T [K]
Den Fehler der Anzahl der Interferenzmaxima ∆m haben wir entsprechend der subjektiven Einschätzung
festgelegt, ob die jeweilige Farbe der Spektrallinien gut sichtbar oder schwierig zu erkennen war.
8
Versuch E 111 - Jamininterferometer
5.2
Auswertung
5.2.1
Berechnung von (n-1)
Durch das Evakuieren der einen Argonkammer ändert sich die optische Weglänge eines Strahls im Vergleich
zum zweiten. Für die optische Weglänge in den Kammern gilt:
~
l = n⋅l
(20)
~
l
n
l
mit
= optische Weglänge
= Brechungsindex
= Kammerlänge (367 ± 1 mm)
Bei evakuierter Kammer gilt dort der Brechungsindex des Vakuums: n=1. Damit ergibt sich für die Differenz
der optischen Weglängen:
~
~
l Argon − lVakuum = (n − 1) ⋅ l
oder
(n − 1) =
(21)
~
~
l Argon − lVakuum
(22)
l
Die Differenz der beiden optischen Weglängen entspricht aber genau dem ganzzahligen Vielfachen der
eingestrahlten Wellenlänge m·λ. Damit ergibt sich folgende Bestimmungsgleichung für (n-1):
(n − 1) = m ⋅ λ
(23)
l
und
(n − 1)−1 =
l
m⋅λ
Die Korrektur auf Normalbedingungen ergibt:
(n − 1)−1 =
0
1
l
⋅
m⋅λ K
(24)
Der Fehler ergibt sich nach dem Gaußschen Fehlerfortpflanzungsgesetz:
∆(n − 1) =
−1
l
l
1
∆l + −
∆m + −
∆λ
2
mλ
mλ2
λm
(25)
bzw.
∆(n − 1)0 =
−1
1
mλK
∆l + −
l
l
l
∆m + −
∆λ + −
∆K
2
2
mλ K
mλK 2
λKm
(26)
Dabei gehen wir aus von:
∆l
∆m
∆λ
∆K
= 1 mm
= siehe Tabelle
= 0 nm
= 0,005 (mit ∆T=0,02 K, ∆p=5 mbar und ∆T0, ∆p0=0,01)
Die auf diese Weise ermittelten Brechzahlen und die auf Normalbedingungen korrigierten Werte sind in der
nachstehenden Tabelle zusammengefasst.
9
Versuch E 111 - Jamininterferometer
Wellenlänge
λ
Cd rot
643,85 nm
Hg gelb
576,96 nm
Hg grün
546,07 nm
Cd grün
508,58 nm
Cd blau
467,88 nm
Hg indigo
435,83 nm
ν2 [Hz2]
2,1681·10-29
2,6999·10-29
3,0140·10-29
3,4747·10-29
4,1056·10-29
4,7316·10-29
K
(n-1)
(n-1)0
(n-1)0-1
∆(n-1)0-1
1,0669
2,4210·10-4
2,5830·10-4
3,8714·103
197,01
1,0676
2,5263·10-4
2,6970·10-4
3,7078·103
181,96
1,0651
2,5468·10-4
2,7126·10-4
3,6865·103
163,89
1,0657
2,5782·10-4
2,7476·10-4
3,6396·103
160,15
1,0589
2,6783·10-4
2,8361·10-4
3,5260·103
104,61
1,0590
2,4551·10-4
2,5999·10-4
3,8463·103
121,88
1,0688
2,6039·10-4
2,7831·10-4
3,5931·103
108,73
1,0679
2,4944·10-4
2,6639·10-4
3,7540·103
152,94
1,0683
2,5498·10-4
2,7240·10-4
3,6711·103
146,89
1,0679
2,4605·10-4
2,6275·10-4
3,8059·103
185,95
1,0683
2,6390·10-4
2,8192·10-4
3,5471·103
163,35
1,0687
2,6900·10-4
2,8748·10-4
3,4785·103
157,64
1,0662
2,6245·10-4
2,7982·10-4
3,5737·103
269,06
1,0665
2,5295·10-4
2,6976·10-4
3,7069·103
288,53
1,0665
2,3988·10-4
2,5583·10-4
3,9088·103
319,23
10
Versuch E 111 - Jamininterferometer
5.2.2
Graphische Darstellung der Messergebnisse und lineare Regression
4500
4400
Linear Fit of Data1_B
4300
4200
4100
(n-1)
-1
0
4000
3900
3800
3700
3600
3500
3400
3300
3200
2,00E+029
3,00E+029
4,00E+029
2
5,00E+029
2
ν [Hz ]
Die gewichtete lineare Regression ergab folgende Regressionsgerade:
y = b + ax = (3751,26 ± 205,82) – (2,7044·10-28 ± 6,2012·10-28 s-2) x
(n-1)-1 = b + a ν2 = (3751,26 ± 205,82) – (2,7044·10-28 ± 6,2012·10-28 s-2) ν2
Die Korrelation beträgt hier nur rund 10%.
5.2.2.1
Bestimmung der Oszillatorstärke fo
Nach Gleichung (18) ergibt sich die Oszillatorstärke aus der Steigung a der Regressionsgeraden nach:
f0 = −
Mit
8π 2 ε 0 m
(27)
N 0e2a
ε0
me
e
N0 =
= 8,8542 ·10-12 AsV-1m-1
= 9,1095 ·10-31 kg
= 1,3806 ·10-23 JK-1
p0
= 2,5033 ⋅ 10 25 m −3
kT0
Der Fehler der Oszillatorstärke berechnet sich nach:
11
Versuch E 111 - Jamininterferometer
∆f 0 =
8π 2 ε 0 m
∆a
N0e2a 2
(28)
Somit erhalten wir:
f 0 = 3,6644 ± 8,40
Der Literaturwert1 für die Oszillatorstärke beträgt f0 = 4,62. Damit ergibt sich eine Abweichung unseres
ermittelten Wertes von 26%. Auffällig ist jedoch der sehr große Fehler (siehe Fehlerdiskussion). Dennoch
liegt f0 zumindest in der Größenordnung des Literaturwertes.
Bestimmung der Resonanzfrequenz ν0
5.2.2.2
Aus Gleichung (19) folgt:
ν0 =
b
−a
(29)
Für den Fehler in ν0 erhalten wir:
∆ν 0 =
1
2 − ab
∆b +
b
2 (− a )
3
∆a
(30)
Damit lautet der für die Resonanzfrequenz ermittelte Wert:
ν 0 = 3,7244 ⋅ 1015 ± 4,3727 ⋅ 1015 Hz
Literaturwert1: ν0 (Argon)= 4,230·1015 Hz
Es ergibt sich eine Abweichung des ermittelten Wertes von 12%.
Berechnung der statischen Dielektrizitätskonstante ε0
5.2.2.3
Ausgehend von Gl. (16) erhalten wir:
n=
1 + aν 2 + b
aν 2 + b
(31)
Unter Verwendung der Maxwellsche Beziehung n = ε liefert uns (31) beim Grenzübergang ν Æ 0 die
statische Dielektrizitätskonstante ε0:
1
b


2
ε 0 = n 2 =  + 1
(32)
Den Fehler in ε0 ermitteln wir gemäß:
1
„Lehrbuch der theoretischen Physik“, Band III, Dr. Siegfried Flügge
12
Versuch E 111 - Jamininterferometer
1  1
∆ε = − 2 + 1 2 ∆b
b b
(33)
ε 0 = 1,0005332 ± 2,9620 ⋅ 10 −5
Literaturwert1: ε0 (Argon)= 1,000554
6.
Fehlerdiskussion
Die mit Sicherheit bedeutendste (statistische) Fehlerquelle ist die Unsicherheit in der Zahl der
Interferenzmaxima m. Zwar wurde für jede Spektrallinie die Messung mindestens zweimal durchgeführt, dies
verhinderte dennoch nicht eine teilweise starke Streuung der Werte. Zur Unsicherheit trugen bei:
1.
Einige Spektrallinien waren für das Auge wesentlich schlechter wahrnehmbar als die grüne HgLinie. Auch die Intensität der Linien variierte. Dies führte dazu, dass ein hohes Maß an
Konzentration bei der Auszählung erforderlich war. Da die Messungen jeweils einige Minuten
dauerten, ermüdete das Auge und die Genauigkeit bei der Bestimmung von m nahm ab. Besonders
gegen Ende der Messung können sich durch häufiges Blinzeln und anschließendes Neuorientieren
im Sucherbild Fehler ergeben haben.
2.
Das Bild des Fernrohrs war nur ein Stück hinter dem Okular scharf wahrnehmbar. Man konnte sich
daher nicht an der Okularmuschel anlehnen, so dass während der Messung das Sucherbild leicht aus
den Augen verloren wurde. Die in dieser Zeit vorbeilaufenden Interferenzstriche mussten dann
geschätzt werden.
3.
Nachdem sich bei vollständiger Öffnung des Dosierventils keine Änderungen am Interferenzbild
mehr ergaben, wurde zusätzlich Ventil C geöffnet. Dabei wanderten zwischen 2 und 5
Interferenzmaxima sehr schnell vorbei, so dass die exakte Zahl nur geschätzt werden konnte.
Neben dieser sollten noch weitere (systematische) Fehlerquellen beachtet werden:
6.1
1.
Unvollständige Evakuierung der Messkammer:
Diesen Fehler schätzen wir als sehr gering (∆m<1 Streifen) ein, da sich gegen Ende der Messung
kaum noch Änderungen des Interferenzmusters ergaben.
2.
Wir schätzen die Wahrscheinlichkeit von Lufteintritten in die Apparatur als ziemlich gering ein. Es
wurde gründlich mit Argon gespült und die evakuierte Apparatur hielt den unteren Druckwert für
einige Minuten. Der Fehler sollte unter 1 Streifen betragen.
3.
Verunreinigung des verwendeten Argongases:
Beimischungen anderer Gase könnten die Messung verfälschen. Die Verunreinigungen bewegen
sich jedoch im Promillebereich und dürften keinen großen Einfluß auf das Messergebnis haben.
4.
Fehler bei Druck-, Temperatur-, Längenmessungen:
Diese Fehler verursachen Änderungen der betrachteten Bestimmungsgrößen <<1 %. Darüberhinaus
können für die gegebenen Literaturwerte (Standardbedingungen etc.) Messgenauigkeiten von
mindestens 2 Nachkommastellen angenommen werden.
Bewertung
Insgesamt überwiegt der Zählfehler von m deutlich. Für jede Messung wurde ∆m geschätzt und angegeben.
Aus den unsicheren Zählwerten für m resultierte eine geringe Korrelation der linearen Regression von (n-1)-1
gegen ν2. Dies drückt sich auch in den Fehlern der Steigung und des Achsenabschnitts aus. Besonders die
13
Versuch E 111 - Jamininterferometer
Steigung der Regressionsgeraden ist stark fehlerbehaftet. Der Fehlerbereich liegt hier schon bei einem
Vielfachen des eigentlichen Wertes, so dass die Bestimmung von f0 und ν0 über die angewendete Methode
fragwürdig ist. Der Achsenabschnitt erscheint besser definiert und es ergibt sich ein annehmbarer Wert für
die Approximation von ε0.
Allein der Einsatz einer Gewichtung über den Fehler von (n-1)-1 bei der Regression ermöglicht physikalisch
einigermaßen sinnvolle Ergebnisse. Einfache lineare Regression oder Regression mit vorheriger
Mittelwertbildung der verschiedenen mi einer Spektrallinie führt nicht zum Ziel.
Die Methode scheint zur Aufnahme der Dispersionskurve und zur Ermittlung von f0, ν0 und ε0 des Gases
Argon nur sehr bedingt geeignet. Sie liefert zwar Ergebnisse in der Größenordnung der Literaturwerte, ist
aber sehr fehlerbehaftet, da die Hauptfehlerquelle hier in einer „manuellen“ Bestimmung der Zahl der
vorbeiwandernden Interferenzmaxima m besteht. Der Fehler ∆m dieser Größe liegt um Größenordnungen
über denen anderer Größen und wirkt sich dementsprechende auf die Ergebnisse aus. Eine Verbesserung der
experimentellen Gegebenheiten sollte demnach auch bei der Auszählung dieser Maxima beginnen. Bessere
Ergebnisse ließen sich vermutlich durch eine automatisierte, computerunterstützte Auszählung erhalten. Der
„Risikofaktor Mensch“ könnte auf diese Weise minimiert werden.
7.
Literatur
Siegfried Flügge
„Lehrbuch der theoretischen Physik“, Band III
Springer, 1961
„Praktische Physik 1“
F. Kohlrausch
Teubner, 1968
14