Ausblick: Brokkolibaum

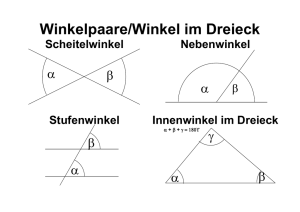
Einen Pythagorasbaum erhielten wir, indem wir zueinander ähnliche
rechtwinklige Dreiecke auf die Quadrate gesetzt haben. In der Regel wird der
Baum gleich entwickelt. Das heißt auf jedes Quadrat wird ein ähnliches
Dreieck gesetzt und auf jede Kathete wieder ein Quadrat. Es entstehen dabei
die verschiedensten Blattgrößen. (siehe z.B. Bild 5 vom Plakat „Was sind
Fraktale?“, 1. Spalte ganz unten)
Fordert man diesen strengen Aufbauplan eines Pythagorasbaumes nicht mehr,
so kann man unter bestimmten Bedingungen Pythagorasbäume erstellen, die
beim Entwickeln nur zwei verschiedene Blattgrößen besitzen.
Falls es nun zwei verschieden große Blätter geben soll, so muss gelten:
1. Fall: Das Quadrat über der kurzen roten Kathete ist genau so groß wie das
Quadrat über der kurzen gelben Kathete (linkes untere Bild)
Da das Quadrieren keine Äquivalenzumformung ist, muss eine Probe durchgeführt
werden. Die Durchführung der Probe bestätigt die Lösungen!
Spielerei mit dem Pythagorasbaum
Für welche rechtwinkligen Dreiecke ist es möglich, jeden
Pythagorasbaum durch Hinzufügen von weiteren Dreiecken und
Quadraten so wachsen zu lassen, dass er höchstens zwei verschiedene
Größen von Blättern besitzt?
x = – 1 nicht möglich, da es keine negativen Strecken geben kann
x = + 1 nicht möglich, da x<1 sein muss!
Da das Quadrieren keine Äquivalenzumformung ist, muss eine Probe durchgeführt
werden. Die Durchführung der Probe bestätigt die Lösung!
2. Fall: Das Quadrat über der langen roten Kathete ist genau so groß wie das
Quadrat über der kurzen gelben Kathete (linkes untere Bild)
nur eine Blattgröße:
Für ein gleichschenklig rechtwinkliges Dreieck erhalten wir bei gleicher
Entwicklung des Baumes einen Pythagorasbaum mit gleich großen Blättern
(linkes obere Bild).
Verwenden wir ein ungleichschenkliges Dreieck, so erhalten wir bei gleicher
Entwicklung den Fall 1 (vom linken unteren Bild), also einen Baum mit nicht
nur einer Blattgröße.
genau zwei Blattgrößen:
>entweder:
Wir müssen den Baum mit nur einer Blattgröße (also den Baum mit dem
gleichschenklig rechtwinkligen Dreieck) an einigen Stellen einmal
weiterentwickeln, an den anderen dagegen bleibt er gleich.
>oder:
Wir versuchen den Baum mit dem ungleichschenkligen rechtwinkligem
Dreieck, durch entsprechende Seitenwahl und entsprechendes Entwickeln, so
zu gestalten, dass nur zwei Blattgrößen vorhanden sind. Konzentrieren wir uns
auf das linke untere Bild. Fall 1 scheidet aus, da immer mehr als zwei
Blattgrößen vorhanden sind. Wir müssen den Baum verschieden entwickeln.
Im Fall 2 wurde das Quadrat über der kürzeren Kathete des Dreiecks
weiterentwickelt. Dies liefert mindestens drei verschiedene Blattgrößen.
Es bleibt also nur noch die Möglichkeit das Quadrat über der längeren Kathete
weiterzuentwickeln. Dies ist der Fall 3. Wir versuchen nun für den Fall 3 die
Katheten so zu wählen, dass das gelbe Quadrat über dem gelben Dreieck genau
so groß ist wie eines der gelben Quadrate über dem roten Dreieck.
linkes unteres Bild, Fall 3:
Hypotenuse des gelben Dreiecks sei 1.
Längere Kathete dieses Dreiecks sei x.
daraus ergibt sich:
Es gilt für das Verhältnis der längeren Kathete zur kürzeren Kathete:
Nur für diesen Fall gibt es zwei verschieden Blattgrößen. (Bild linke Spalte
rechts unten)
Ausblick: Brokkolibaum
Eine Verallgemeinerung der Idee des Pythagorasbaumes besteht darin,
Quadrate nicht über den Katheten eines rechtwinkeligen Dreiecks, sondern
über den beiden Schenkeln eines
gleichschenkeligen Dreiecks zu errichten.
Da die Hypotenuse des roten Dreiecks x ist, können wir mit Hilfe der
Ähnlichkeit der beiden rechtwinkligen Dreiecke (rot und gelb) die Größen
der Katheten des roten Dreiecks berechnen:
Wählt man als Basiswinkel des gleichschenkeligen Dreiecks den Winkel α =
60°, so erhält man einen Baum über einem gleichseitigen Dreieck, der eine
interessante Parkettierung der Ebene erzeugt.