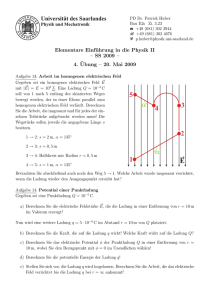
Lösung der 4.¨Ubung

IS
R
S
SA
PD Dr. Patrick Huber
Bau E26 Zi. 3.23
T +49 (681) 302 3944
v +49 (681) 302 4676
k [email protected]
S
UN
E R SIT
A
IV
A VIE N
Elementare Einführung in die Physik II
– SS 2009 –
Lösung der 4. Übung – 20. Mai 2009
Aufgabe 13: Arbeit im homogenen elektrischen Feld
R
Wegen W = F~ ·d~s muss nur entlang den Wegen parallel zu den Feldlinien Arbeit verrichtet werden
bzw. wird nur entlang den Wegen parallel zu den Feldlinien Arbeit verrichtet (je nach Vorzeichen
der Ladung und Bewegungsrichtung). Damit wird
1 → 2:
√
W = Q E (−s) sin(α − 90◦ ) = − 2 J ≈ −1.414 J
(1)
W = Q E (−s) = −0, 5 J
(2)
W = 0J
(3)
1
W = Q E (−s) sin(α − 90◦ ) = − √ J ≈ −0, 707 J
2
(4)
2 → 3:
3 → 4:
4 → 5:
Die aufsummierte Arbeit ist W ≈ −2, 62 J. Sie ist negativ, also muss die Arbeit von Ihnen verrichtet
werden. Zurück zum Punkt 1 wird dann aber wieder genau diese Arbeit vom System verrichtet (also
W = +2, 62 J), so dass die insgesamt geleistete Arbeit W = 0 J beträgt. Das System ist konservativ.
Aufgabe 14: Potential einer Punktladung
a) Das elektrische Feld einer positiven Punktladung Q zeigt radial nach außen von der Ladung
weg. Der Betrag der Feldstärke als Funktion des Abstandes r ist
E(r) =
1 Q
.
4 π 0 r2
(5)
V
Es ist also E(10 m) = 898, 8 m
.
b) Die Kraft auf die Ladung q ist
F = E(10 m) q = 4, 49 mN .
(6)
Entsprechend wirkt auf Q eine betragsgleiche, aber entgegengesetzt gerichtete Kraft, die von
q hervorgerufen wird (actio = reactio).
Rr
c) Das Potential der Punktladung Q ist φ(r) = − ∞ E(r) dr, also
φ(r) =
1 Q
+C.
4 π 0 r
Die Integrationskonstante C wird wegen φ(∞) = 0 zu Null. Es ist also φ(10 m) = 8988 V.
(7)
d) Die potentielle Energie Wpot der Ladung q im elektrischen Feld der Ladung Q ist
Wpot = φ(10 m) q = 44, 9 mJ .
(8)
e) Die vom System verrichtete Arbeit W entspricht gerade der Differenz der potentiellen Energie,
also
W = Wpot (10 m) − Wpot (∞) = q [φ(10 m) − φ(∞)] = 44, 9 mJ .
(9)
| {z }
=0
Aufgabe 15: Bewegung im elektrischen Feld
a) Welche Spannung U muss ein Elektron durchlaufen, damit es aus der Ruhe auf die Geschwindigkeit ~v0 gebracht wird?
Die Energie, die das Elektron im elektrischen Feld gewinnt, wird in kinetische Energie umgesetzt:
1
Ekin =
· m · v02 = U · e
(10)
2
r
2·U ·e
⇒ v0 =
(11)
me
b) Bei welcher Spannung erreicht das Elektron 10% der Lichtgeschwindigkeit (angenommene
Grenze für klassische Rechnung)?
Auflösen von (1) gibt:
me · (0, 1c)2
2·e
= 2556, 8 V
U =
(12)
(13)
c) Ein Elektron tritt mit der Anfangsgeschwindigkeit ~v0 in ein räumlich begrenztes, homogenes
~ ein. Wie verläuft die weitere Bewegung? Fallunterscheidung
elektrisches Feld der Stärke E
mit Skizzen der Flugbahnen.
Fallunterscheidung: Feld parallel & senkrecht zur Flugbahn
Skizzen: Elektron wird beschleunigt // abgelenkt
d) Wie lauten die quantitativen Beschreibungen des Ortes ~r(t) und der Geschwindigkeit ~v (t) als
Funktionen der Zeit, wenn das Elektron parallel zu den Platten zwischen zwei Kondensatorplatten hindurchfliegt (Anfangsgeschwindigkeit ist v0 )?
Tipp: Betrachten Sie x- und y- Komponente in einem geeigneten Koordinatensystem separat.
Es gilt: F = E · q = m · a
Wichtig: Die Aufspaltung in x- und y-Komponente der Flugbewegung. Die unabhängige Betrachtung führt auf
vy (t) = v0 = const
qe
·t
vx (t) = E ·
me
ry (t) = y0 + v0 · t
1
qe 2
rx (t) = x0 + · E ·
·t
2
me
(14)
(15)
(16)
(17)
Aufgabe 16: Millikan-Versuch
Ist der Tropfen im Gleichgewicht, so gilt (Die Auftriebskraft ist vernachlässigbar, da die Dichte der
Luft weniger als ein Prozent der des Öls beträgt):
mg = qE
(18)
mit
4
m = πR3 ρ
3
(19)
Somit gilt:
mg
E
4πr3 ρg
=
3E
= 8, 0 · 10−19 C
q=
(20)
(21)
(22)
(23)
q
8, 0 · 10−19 C
=
e
1, 60 · 10−19 C
=5
(24)
(25)