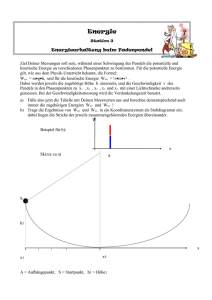
E=U/d

Potential, Potentialunterschied und Spannung
24.08.2016
+
S1
S2
-
•
Angezogen von der positiven Seie des Plattenkondensators führt das Elektron eine
beschleunigte Bewegung aus und bewegt sich mit wachsender Geschwindigkeit von S2 nach
S1. Die Strecke S2-S1 wird im Folgenden mit d abgekürzt.
•
Wkin des Elektrons kommt aus der Fähigkeit des elektrischen Feldes, Arbeit verrichten zu
können. Die potenziellen Energie des Elektrons am Punkt S2 in Bezug auf die positive Platte
des Kondensators wird in kinetische Energie umgewandelt indem Beschleunigungsarbeit
verrichtet wird. Nach Durchlaufen der Stecke d hat das Elektron die kinetische Energie
Wkin=1/2mv2 aufgenommen.
•
Wegen des Energieerhaltungssatzes muss die umgewandelte potentielle Energie des
elektrischen Feldes gleich der vom Elektron aufgenommenen kinetischen Energie sein.Es
gilt: Wpot(el.-Feld) =Wkin(Elektron)
•
Daraus ergibt sich Wpot=Wkin=1/2mv2. Mit v=a*t ergibt sich:
(A)
•
Für die Beschleunigung gilt wegen F=ma und E=F/q:
(1)
•
Wpot=Wkin=1/2mv2=1/2ma2t2.
a=F/m=(qE)/m e
(B)
Da es sich um eine beschleunigte Bewegung handelt gilt:
d=1/2at2 und die Umstellung nach t2 ergibt:
(2)
t2=(2d)/a
Setzt man die Beziehung aus (B) für a in (2) ein so ergibt sich:
(3)
•
t2= (2dme)/(qE)
Setzt man jetzt die in (1) und (2) gefundenen Beziehungen für a und t in (A) ein so ergibt
sich:
Wpot=Wkin=1/2mv2=1/2ma2t2=1/2*me*(q2E2/me2)*((2dme)/(qE))
Potential, Potentialunterschied und Spannung
24.08.2016
•
Nach Vereinfachen durch Kürzen wird daraus:
(4)
Wpot=Wkin=q*E*d
Dieser Ausdruck beschreibt die potentielle Energie, die ein Elektron oder eine Ladung q im
homogenen Feld eines Plattenkondensators mit den Bezugspunkten S2 und S1 besitzt. Diese
Energie ist abhängig von der Größe der Probeladung.
•
Der Potentialbegriff beschreibt jedoch die Fähigkeit eines elektrischen Feldes, Arbeit zu
verrichten. Diese Fähigkeit besitzt es auch ohne Probeladung. Eine
•
Potentialdifferenz besteht also auch ohne Ladung und ist eine Eigenschaft des elektrischen
Feldes zwischen zwei Punkten.
•
Diese Potentialdifferenz ist von der Ladung unabhängig und wird als
(5)
Δφ=Wpot/q=E*d
(siehe (4)) definiert.
•
Jetzt ist der Wert Δφ nicht mehr von der Ladung q abhängig, da bei doppelter (dreifacher,
vierfacher…) Ladung Wpot auch doppelt (dreifach, viefach …) so groß wird. Der Quotient
Δφ=Wpot/q bleibt somit gleich und beschreibt die Fähigkeit des Feldes, Arbeit zu
verrichten.
•
Wegen d = S2-S1 wird φ als Potenzialunterschied oder auch Spannung zwischen den
Punkten S2 und S1 genannt. Es gilt:
(6)
Δφ=Wpot/q =U also
U= E*d und auch
E=U/d (Einheit V/m).
•
Der Ausdruck φ=q*E*S1 wird Potential eines elektrischen Feldes an einem Punkt S1 gegen
Unendlich genannt. Der Potentialunterschied Δφ zwischen zwei Punkten mit jeweils
einem Potenzial gegen Unendlich nennt man Spannung zwischen zwei Punkten.