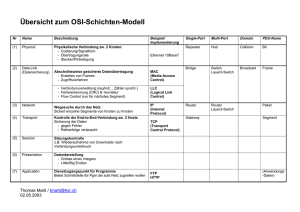
Graph Coloring - Chair 11: ALGORITHM ENGINEERING

Kap. 5: Graph Coloring
Professor Dr. Petra Mutzel
Lehrstuhl für Algorithm Engineering, LS11
10./11. VO
18.12.06 / 8.1.07
Überblick
• 5.1 Einführung
– Definition und Motivation
– Sudoku
• 5.2 ILP-Formulierungen für Sudoku
– Branch-and-Cut Algorithmus
– Praxistest für Sudoku-Instanzen
• 5.3 ILP-Formulierungen für
Färbungsprobleme
– Spaltengenerierung zur Lösung des ILP mittels
maximum weight independent set
2
Literatur
• V. Kaibel und T. Koch: Mathematik für den Volkssport,
ZIB-Report 06-28, Mai 2006 (Sudoku)
• A. Mehrotra und M.A. Trick: A column generation
approach for graph coloring, INFORMS Journal on
Computing, vol. 8, no. 4, 344-354, 1996
• (nur für aktuelle Literatur☺ P. Hansen, M. Labbe, und D.
Schindl, Set covering and packing formulations of graph
coloring: algorithms and first polyhedral results, 2005)
3
5.1 Einführung
• Sei G=(V,E) ein ungerichteter Graph.
• Eine (Knoten-)Färbung (Coloring) von G ist eine
Zuordnung von je einer Farbe zu jedem Knoten, so dass
die Endknoten jeder Kante unterschiedlich gefärbt sind.
• Die kleinste Anzahl von Farben die für einen gegebenen
Graphen G benötigt wird, heißt die chromatische Zahl
von G: χ(G).
• Das Problem: „Existiert für G eine Färbung mit
höchstens k Farben?“ (Kurzform: „Ist G k-färbbar?“) ist
NP-vollständig.
• Das Problem bleibt NP-vollständig für planare Graphen
mit Maximalgrad 4.
4
Eigenschaften
Es gilt:
•
•
•
•
•
•
χ(G) = 1 ⇔ E=∅
χ(G) ≥ 3 ⇔ G besitzt einen ungeraden Kreis
χ(G) ≥ Cliquenzahl ω(G)
χ(G) ≤ Δ(G)+1
χ(G) ≤ Δ(G) ⇔ (G ist nicht vollständig) und (G ist
nicht ungerader Kreis)
χ(G) ≤ 4 für planare Graphen
5
Anwendungen
• Landkartenfärbung: Länder sollen so eingefärbt
werden, dass zwei benachbarte Länder unterschiedliche
Farben erhalten.
• Berühmt wurde der Beweis zum Vierfarbensatz: „Jeder
planare Graph ist 4-färbbar“. Der Beweis von Appel und
Haken 1976 war der erste weltweit anerkannte
Computerbeweis.
• Frequenzzuordnung in Telekommunikationsnetzen
• Computer Register Allokationsproblem
• Stundenplanerstellung (time tabling)
6
Sudoku
Aufgabe: Vervollständige die Matrix, so dass in jeder Zeile,
in jeder Spalte und in jedem der markierten 3x3 Quadrate
jede der Zahlen 1,2,…,9 genau einmal vorkommt.
8
1
6
2
6
6
1
9
4
3
7
7
7
3
5
1
8
Ein Sudoku besitzt genau eine zulässige Lösung.
5.2 Sudoku: Mathematische Formulierung
Variablen: xijk für i,j,k=1,…,9 mit
Zuordnungsproblem
xijk=1 ⇔ Feld i,j wird mit Farbe k gefärbt.
Constraints: Für jede Farbe k muss für jede Zeile i gelten:
9
∑ xijk = 1 für k,i=1,…,9.
j =1
Für jede Farbe k muss für jede Spalte j gelten:
9
∑ xijk = 1 für k,j=1,…,9.
i =1
Für jede Farbe k muss für die 3x3 Quadrate Q(a,b) gelten:
∑
xijk = 1 für k,j=1,…,9. Dabei ist a,b∈{1,2,3}
i,j∈Q(a,b)
Für jedes Feld i,j gelten: es muss eine Farbe erhalten:
9
∑ xijk = 1 für i,j=1,…,9. 729 Variablen, 4x81=324 Gleichungen
k=1
Visualisierung der Variablen xijk für unser Beispiel: dabei
wird k als Höhe/Farbe dargestellt; die Einträge werden als
Würfel (vorgegeben) oder Kugel angezeigt und
repräsentieren die Einträge im unten liegenden Feld.
In jedem der grauen Bereiche muss genau ein Würfel
bzw. Objekt schweben.
jedes k
jedes i
jedes j
jedes Q(a,b)
Sudoku: Formulierung als Färbungsproblem
Die Knoten des Graphen entsprechen den zu färbenden Feldern.
Es existiert eine Kante für alle Knotenpaare in der gleichen Zeile,
in der gleiche Spalte, und im gleichen ausgezeichneten Quadrat.
kleines Beispiel
mit 2x2 Quadraten
Aufgabe: Finde Färbung
mit 9 Farben (hier:
4 Farben), die
konsistent mit der
geg. Teilfärbung ist.
Sudoku: Mathematische Formulierung
Variablen: xijk für i,j,k=1,…,9 mit
xijk=1 ⇔ Knoten ij wird mit Farbe k gefärbt.
Färbungsproblem
in Graphen
Constraints: Für jede Kante in G eine Ungleichung der Form:
xijk + xi´j´k ≤ 1 für alle adjazenten Paare (ij)(i´j´) und alle
k=1,…,9. Denn: höchstens einer darf die Farbe k erhalten.
Für jeden Knoten ij gilt: er muss eine Farbe erhalten:
9
∑ xijk = 1 für alle Knoten ij.
k=1
Zielfunktion: beliebig ⇒ ganzzahliges lineares Programm
729 Variablen, 3(9x36)+81= 1035 Un-/Gleichungen
Sudoku als Graphenfärbungsproblem: unser Beispiel
Branch & Cut (Grundidee)
• Anwendung
– NP-schwere Optimierungsprobleme
• Branch & Cut
– löst kombinatorische Optimierungsprobleme
exakt (bzw. mit jeder vorgegebenen
Approximationsgüte)
– benötigt exponentielle Zeit
– ist manchmal (oft) praktisch effizient
14
Branch & Cut (Grundidee)
• Identifiziere die zulässigen Lösungen mit 0/1Vektoren
• Beschreibe die konvexe Hülle dieser
Vektoren möglichst gut durch lineare
Ungleichungen
15
Branch & Cut (Grundidee)
Menge der zulässigen Lösungen
16
Branch & Cut (Grundidee)
Konvexe Hülle über diese Menge
17
Branch & Cut (Grundidee)
Zielfunktion
Die Beschreibung der konvexen Hülle durch lineare
Un-/gleichungen ist i.A. nicht bekannt.
19
Branch & Cut (Grundidee)
Lösung: stattdessen Relaxierung der ILP-Formulierung
20
Branch & Cut (Grundidee)
21
Branch & Cut (Grundidee)
Lösungspunkt über die LP-Relaxierung ist aber
nicht zulässig für unser Originalproblem
22
Branch & Cut (Grundidee)
• Identifiziere die zulässigen Lösungen mit 0/1Vektoren
• Beschreibe die konvexe Hülle dieser
Vektoren möglichst gut durch lineare
Ungleichungen
• Finde möglichst gute Algorithmen, die für
einen gegebenen Punkt von diesem verletzte
Ungleichungen finden bzw. feststellen, dass
keine solchen existieren.
Separierung
23
Branch & Cut (Grundidee)
Schnittebene für Separierung
25
Branch & Cut (Grundidee)
26
Branch & Cut (Grundidee)
neuer Lösungspunkt der LP-Relaxierung
28
Branch & Cut (Grundidee)
29
Branch & Cut (Grundidee)
Hinzufügen einer Schnittebene: „schneidet den Punkt weg“
30
Branch & Cut (Grundidee)
Schnittebenenverfahren (Cutting Plane Method)
neuer Lösungspunkt der LP-Relaxierung
→ zulässig und damit optimal
32
Branch & Cut (Grundidee)
Separierungsproblem
• Löse Relaxierungen mit Schnittebenenverfahren.
Cut
• Verzweige, wenn keine Schnittebenen gefunden
werden, aber die Lösung nicht ganzzahlig ist.
Branch
• Finde gute zulässige Lösungen basierend auf
fraktionellen Lösungen.
Exploit
• Schneide nichtprofitable Teilbäume weg.
Bound
33
Branch & Cut (Grundidee)
Bound
Cut
Branch
Eine typische B&C
Berechnung
Maximierungs
Problem
35
Sudoku: Mathematische Formulierung
Variablen: xijk für i,j,k=1,…,9 mit
xijk=1 ⇔ Knoten ij wird mit Farbe k gefärbt.
Färbungsproblem
in Graphen
Constraints: Für jede Kante in G eine Ungleichung der Form:
xijk + xi´j´k ≤ 1 für alle adjazenten Paare (ij)(i´j´) und alle
k=1,…,9. Denn: höchstens einer darf die Farbe k erhalten.
Für jeden Knoten ij gilt: er muss eine Farbe erhalten:
9
∑ xijk = 1 für alle Knoten ij.
k=1
Zielfunktion: beliebig ⇒ ganzzahliges lineares Programm
729 Variablen, 3(9x36)+81= 1035 Un-/Gleichungen
Sudoku: Strong Branching
Strong Branching: Fixiere eine Variable testweise auf 0 oder 1:
Falls die LP-Relaxierung keine zulässige Lösung mehr besitzt,
dann wissen wir: diese Variable muss genau den anderen Wert
annehmen.
Dieser Test wird für beide möglichen Werte aller Variablen
durchgeführt.
Die so ermittelten Werte werden dann fixiert.
Danach wird die LP-Relaxierung berechnet.
Praxistest für Sudoku: In allen Fällen von 15.000 berechneten
Instanzen war der Wert der LP-Relaxierung ganzzahlig und
damit das Sudoku gelöst.
Offenes Problem: Gilt das für alle möglichen Sudokus?
Sudoku in der Praxis
In Praxis genügt bereits:
Ersetzung von Strong Branching durch approximative Verfahren,
wie z.B. Presolving bzw. Probing (Ableitung von einfachen
Implikationen aus dem ILP).
Praxistest für Sudoku: Das Lösen aller getesteten Instanzen
erfolgte innerhalb weniger Sekundenbruchteile.
Sudoku-Server: http://www.matheon.de
Frohe Weihnachten
5.3 ILP-Formulierungen für Graphfärbung
Variablen: xik∈{0,1} für i=1,…,|V| und k=1,…,K mit
xik=1 ⇔ Knoten i wird mit Farbe k gefärbt.
Constraints: Für jede Kante in G eine Ungleichung der Form:
xik + xjk ≤ 1 für alle adjazenten Knoten i und j und alle
k=1,…,K. Denn: höchstens einer darf die Farbe k erhalten.
Für jeden Knoten i gilt: er muss eine Farbe erhalten:
K
∑ xik = 1 für alle Knoten i∈V.
k=1
G ist mit K Farben färbbar, wenn das System eine
zulässige Lösung besitzt
Bestimmen des kleinsten K mittels Binäre Suche
K|V| Variablen und K|E|+|V| Ungleichungen
Probleme bei dieser Formulierung
LP-Relaxierung des ILPs ist ziemlich fraktional (also nicht
nur 0,5-Werte): z.B. xik=1/K für i=1,…,|V| und k=1,…,K ist
eine zulässige Lösung für die LP-Relaxierung.
Viele Symmetrien : Die Variablen für jedes k sind in der
Formulierung absolut identisch
→ Jeder Lösungswert hat exponentiell viele
Repräsentationen (bzgl K)
→ Branching an einer Variablen xi1 führt dazu, dass einfach
eine andere Repräsentation der gleichen Lösung gewählt
wird → keine Fortschritte
→ beide Tatsachen erschweren die Lösung durch
Branch&Bound bzw. Branch&Cut
ILP-Formulierung über Unabhängige
Mengen
Variablen: Sei S die Menge aller maximalen unabhängigen
Mengen von G. Dann sind die Variablen xs∈{0,1} für alle s∈S
mit xs=1 ⇔ die unabhängige Menge s∈S wird als eine Farbe
der Graphfärbungslösung interpretiert.
„maximal“ bzgl. Inklusion: d.h. es gibt keine andere unabhängige
Menge, die s enthält (wenn s maximale unabhängige Menge ist)
Constraints: Für jeden Knoten wird gefordert, dass
∑ xs ≥ 1 für alle Knoten i∈V.
{s:i∈s}
Zielfunktion: Minimiere ∑ xs
s
nur |V| Ungleichungen, aber exponentiell viele Variablen
Bemerkungen zur ILP-Formulierung
Jeder Knoten kann in mehreren unabhängigen Mengen
auftauchen → dies ist aber kein Problem: um eine gültige
Knotenfärbung zu erhalten, wähle einfach eine dieser Farben
für die jeweiligen Knoten aus.
Alternativ könnte man auch die Menge aller unabhängigen
Mengen als Variablen zulassen, aber dann hätte man sehr
viel mehr Variablen → dann könnte man auch Ungleichungen
durch Gleichungen ersetzen.
Problem bei der Formulierung: exponentiell viele Variablen
Lösung durch Spaltengenerierung
Spaltengenerierung für ILPFormulierung
Idee:
1. Beginne nur mit einem kleinen Teil der Variablen: S´⊆S
(dies entspricht einer Teilmenge der Spalten des ILPs).
2. Löse die LP-Relaxierung LPRel bzgl. S´
3. Nun muss man testen, ob diese Lösung auch eine gültige
Lösung der LP-Relaxierung bzgl. S ist. „Pricing“
4.
5.
6.
Falls dies nicht der Fall ist, müssen zusätzliche Spalten
hinzugefügt werden → Re-Optimierung über dem
jetzigen S´ → gehe zu 3.
Sonst: Falls die Lösung von LPRel ganzzahlig ist →
Optimallösung gefunden
Sonst: Branching „Branch&Cut&Price“
Pricing-Problem
Geg. ist eine Lösung x* von LPRel bzgl. S´ ⊆ S. Ist diese
optimal auch bzgl. S?
Minimiere ∑ xs
s
∑ xs ≥ 1 für alle i∈V
{s:i∈s}
0 ≤ xs ≤1
Eine neue Spalte t∈S\S´ kann den Lösungswert nur dann
verbessern, wenn die reduzierten Kosten der dazugehörigen
Variablen kleiner als 0 sind.
Reduzierte Kosten für neue Variable t: ct - π At , wobei
– At die Spalte t der Matrix bezeichnet
– ct der dazugehörige Kostenkoeffizient, und
– π der Lösungswert der dualen Variablen zu Zeile i.
Pricing-Problem
Geg. ist eine Lösung x* von LPRel bzgl. S´ ⊆ S. Ist diese
optimal auch bzgl. S?
Minimiere ∑ xs
s
∑ xs ≥ 1 für alle i∈V
{s:i∈s}
0 ≤ xs ≤1
Suche also eine Spalte t, für die der Wert ct - π At = 1 - π At < 0.
⇔ π At > 1.
Suche also eine maximale unabhängige Menge T (entspricht
Spalte t in A) für die gilt π At > 1.
Bemerkung: Für alle Spalten, die bereits in S´ enthalten sind
gilt: die reduzierten Kosten von Lösung x* sind ≥ 0, sie werden
also nicht wieder ausgewählt.
Pricing-Lösung
Pricing kann durch folgendes Problem gelöst werden. Dabei
sei πi die Lösung von LPRel der dualen Variablen zu Zeile i.
Maximiere ∑ πi zi
i∈V
Maximum weight
s.t.
zi+zj ≤1 für alle i und j mit ij∈E independent set
zi ∈ {0,1}
problem
Falls die optimale Lösung dieses maximum gewichteten
unabhängigen Menge Problems größer als 1 ist, dann
müssen diejenigen zi mit Wert 1 zu S´ hinzugefügt werden.
Andernfalls: die Lösung bzgl. S´ ist auch bereits optimal
bezüglich S (d.h. alle notwendigen unabhängigen Mengen
sind bereits in S´ enthalten).
Maximum Independent Set
Auch das maximum independent set problem ist NPschwierig, aber es wurde bisher sehr gut studiert und es gibt
viele exakte Verfahren, die relativ grosse Instanzen
beweisbar optimal lösen können.
z.B. Branch&Cut
Auch muss das Problem meist nicht exakt gelöst werden, es
genügt, nur eine Menge T zu finden mit Zielfunktionswert > 1.
z.B. Greedy
Exakte Lösung ist nur dann notwendig, wenn Heuristiken
keine solche Menge finden bzw. um zu beweisen, dass keine
solche Menge existiert (am Ende).
„Maximum weight independent set problem“ ist äquivalent
zum „maximum weighted clique problem“ im
Komplementärgraphen.
Branching
Klassisches Branching ist problematisch, weil:
- wird eine Variable für s auf 1 gesetzt → Markiere alle Knoten
in s mit einer neuen Farbe und entferne diese aus G.
-wird eine Variable für s auf 0 gesetzt → die Lösung des
maximum independent set problems könnte genau diese
Variable wieder ausgeben → Problem!
Deswegen: Branching: Seien S1 und S2 zwei maximal
unabhängige Mengen und i,j Knoten mit i∈S1∩S2 und j∈S1\S2
und mindestens einer der beiden Werte ist fraktional. Dann
erzeuge 2 neue Subprobleme:
DIFFER(i,j): d.h. beide müssen verschiedene Farben erhalten
SAME(i,j): beide müssen die gleiche Farbe erhalten.
Branching
DIFFER(i,j) kann erreicht werden, indem eine Kante ij
eingefügt wird.
SAME(i,j) kann erreicht werden indem beide Knoten
miteinander kontrahiert werden.
Die aktuelle Lösung ist für beide neuen Subprobleme nicht
mehr zulässig, wird also dadurch abgeschnitten.
Experimentelle Resultate
Zufällige Graphen: bis zu |V|=70, |E|=2180, Zeit: ≤ 585s (73 s)
Register Allokationsgraphen: bis zu |V|=864, |E|=18707, Zeit: ≤
31s.
Schwierige Graphen: bis zu |V|=23, |E|=71, Zeit: ≤ 9s, aber
nicht |V|=47, |E|=236 innerhalb einer Stunde.
ENDE COLORING