3. Übung Aufgabe 1 Der Modus ist a) der häufigste Wert. b) der Wert

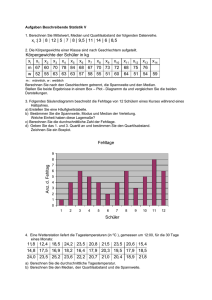
3. Übung
Aufgabe 1
Der Modus ist
a)
der häufigste Wert.
b)
der Wert unter dem 50 % aller anderen Werte liegen.
c)
der Durchschnitt aller Werte.
d)
der Wert mit der größten Häufigkeitsdichte.
e)
der Schwerpunkt einer Häufigkeitsverteilung.
Aufgabe 2
Der Median ist
a)
der häufigste Wert.
b)
der Wert unter dem 50 % aller anderen Werte liegen.
c)
der Durchschnitt aller Werte.
d)
der Wert mit der größten Häufigkeitsdichte.
e)
der Schwerpunkt einer Häufigkeitsverteilung.
Aufgabe 3
Das arithmetische Mittel ist
a)
der häufigste Wert.
b)
der Wert unter dem 50 % aller anderen Werte liegen.
c)
der Durchschnitt aller Werte.
d)
der Wert mit der größten Häufigkeitsdichte.
e)
der Schwerpunkt einer Häufigkeitsverteilung.
Aufgabe 4
Welcher Mittelwert ist robust?
a)
Median
b)
Arithmetisches Mittel
c)
Modus
d)
Harmonisches Mittel
e)
Geometrisches Mittel
Aufgabe 5
Welcher Zusammenhang gilt zwischen der Schiefe einer Verteilung und ihren
Mittelwerten?
a)
Wenn 𝑥̅ ≤ Median ≤ Modus, dann ist die Verteilung linkssteil.
b)
Wenn 𝑥̅ ≤ Median ≤ Modus, dann ist die Verteilung rechtssteil.
c)
Wenn 𝑥̅ ≥ Modus ≥ Median, dann ist die Verteilung linkssteil.
d)
Wenn 𝑥̅ ≥ Modus ≥ Median, dann ist die Verteilung linksschief.
e)
Wenn 𝑥̅ ≥ Median ≥ Modus, dann ist die Verteilung
rechtsschief.
Aufgabe 6
Die Varianz ist die
a)
mittlere absolute Abweichung zum Median.
b)
mittlere absolute Abweichung zum arithmetischen Mittel.
c)
mittlere quadratische Abweichung zum Median.
d)
mittlere quadratische Abweichung zum arithmetischen Mittel.
e)
die quadrierte Standardabweichung.
Aufgabe 7
Die Spannweite ist
a)
der Quotient aus Quartilsabstand und dem doppelten Median.
b)
der Abstand zwischen erstem und drittem Quartil.
c)
die Wurzel aus der Varianz.
d)
der Abstand zwischen kleinstem und größtem Wert.
e)
der Quotient aus Standardabweichung und arithmetischem
Mittel.
Aufgabe 8
Der Quartilsabstand ist
a)
der Quotient aus Quartilsabstand und dem doppelten Median.
b)
der Abstand zwischen erstem und drittem Quartil.
c)
die Wurzel aus der Varianz.
d)
der Abstand zwischen kleinstem und größtem Wert.
e)
der Quotient aus Standardabweichung und arithmetischem
Mittel.
Aufgabe 9
Die Standardabweichung ist
a)
der Quotient aus Quartilsabstand und dem doppelten Median.
b)
der Abstand zwischen erstem und drittem Quartil.
c)
die Wurzel aus der Varianz.
d)
der Abstand zwischen kleinstem und größtem Wert.
e)
der Quotient aus Standardabweichung und arithmetischem
Mittel.
Aufgabe 10
Eine Stichprobe ergab folgende Merkmalswerte: 1; 2; 7; 8; 7; 5; 8; 2. Berechnen Sie die
Spannweite.
a)
2
3
b)
2,5
c)
4
d)
7
e)
7,5
Aufgabe 11:
In einem Betrieb wurden der laufenden Produktion 25 fertiggestellte Wellen
entnommen. Die Messung ihrer Länge (in mm) brachte folgendes Ergebnis:
𝑣
𝑥𝑣
𝑣
𝑥𝑣
𝑣
𝑥𝑣
𝑣
𝑥𝑣
𝑣
1
2
3
4
5
29,9
29,7
30,2
29,8
30,3
6
7
8
9
10
30,2
30,0
30,1
30,2
30,0
11
12
13
14
15
30,0
30,1
29,9
29,6
30,3
16
17
18
19
20
30,4
29,7
30,5
29,8
29,9
21
22
23
24
25
𝑥𝑣
30,0
29,9
29,8
30,1
30,0
a) Stellen Sie die Häufigkeitsverteilung und die empirische Verteilungsfunktion
graphisch dar!
b) Teilen Sie die Beobachtungswerte in linksoffene Klassen mit ∆(𝑥𝑖 ) = const. = 0,1 mm
ein und stellen Sie das Ergebnis in Form eines Histogramms und einer appoximierenden
Verteilungsfunktion graphisch dar! Begründen Sie die Wahl von 𝑥̃0 !
c) Ermitteln Sie mit Hilfe der approximierenden Verteilungsfunktion (vgl. b)) einen
Bereich, in dem sich 80% der Beobachtungswerte befinden!
d) Teilen Sie die Beobachtungswerte wie folgt in linksoffene Klassen ein:
𝑥̃0 = 29,55, Δ(𝑥1 ) = Δ(𝑥6 ) = 0,1 𝑚𝑚, Δ(𝑥2 ) = Δ(𝑥3 ) = Δ(𝑥4 ) = Δ(𝑥5 ) = 0,2 𝑚𝑚!
Zeichnen Sie das zugehörige Histogramm!
Aufgabe 12:
Bei der Prüfung der Tragfähigkeit von Plastik-Tragetaschen der Sorten A und B ergaben
sich folgende Häufigkeitsverteilungen:
Tragkraft von … bis unter …. kg
unter 6,4
6,4 – 7,4
7,4 – 8,4
8,4 – 9,4
9,4 -10,4
10,4 – 11,4
11,4 – 12,4
12,4 – 13,4
13,4 – 14,4
14,4 und mehr
Anzahl der Tragetaschen
Sorte A
Sorte B
16
6
16
4
30
14
84
35
136
67
98
48
50
22
36
20
24
0
10
4
Charakterisieren und vergleichen Sie die beiden Verteilungen mit Hilfe geeigneter
Maße/Verfahren!
Aufgabe 13:
Die folgenden Häufigkeitsverteilungen eines klassierten metrischen Merkmals sind
durch geeignete Maßzahlen zu charakterisieren!
Klassen
130 b. u. 150
150 b. u. 170
170 b. u. 190
190 b. u. 210
210 b. u. 230
230 b. u. 250
250 b. u. 270
(1)
(2)
(3)
𝑛𝑖
𝑛𝑖
𝑛𝑖
2
10
42
92
42
10
2
0
12
52
72
52
12
0
2
12
50
58
76
2
0
Kommentieren Sie die Ergebnisse!
Stellen Sie die Verteilungen graphisch dar.
Aufgabe 14:
Über die Zuverlässigkeitsuntersuchung spezieller Kühlaggregate eines Herstellers
wurde in einer Zeitschrift eine Häufigkeitstabelle für gruppierte Daten veröffentlicht. Es
wurden Anzahlen von Kühlaggregaten ermittelt, die in bestimmte Lebensdauerklassen
fallen:
Klasse
𝐾1
𝐾2
𝐾3
𝐾4
𝐾5
𝐾6
𝐾7
𝐾8
𝐾9
𝐾10
Lebensdauer in Stunden
Anzahl
[0, 100)
[100, 200)
[200, 300)
[300, 500)
[500, 1000)
[1000, 1500)
[1500, 2000)
[2000, 2500)
[2500, 3000)
[3000, 4000)
2
0
18
49
169
98
87
44
32
1
a) Bestimmen Sie alle Kenngrößen, die zur Lösung von b) benötigt werden. Dabei ist
zu beachten, dass die Klassenbreiten nicht gleich sind.
b) Stellen Sie Histogramm, Häufigkeitspolygon, Summenpolygon und empirische
Verteilungsfunktion graphisch dar.
c) Kann aufgrund der erhobenen Daten etwas gegen die Werbung des Herstellers
eingewendet werden, dass maximal 4% seiner Produkte weniger als 300 Stunden
funktionieren?
Aufgabe 15:
Eine Textilfirma analysiert vor Beginn eines neuen Produktionsvorhabens die
Größenverteilung eines gewissen Kundenkreises. Dabei wurden u. a. auch die
Körpergrößen (in cm) einer Gruppe von 30 Studenten ermittelt:
180,
182,
170,
176,
165,
177,
167,
175,
183,
180,
172,
179,
177,
172,
172,
166,
173,
166,
160,
179,
163,
176,
166,
176,
176,
162,
177,
164,
168,
181.
a) Bestimmen Sie für die Klasseneinteilung
[160, 165), [165, 170), [170, 175), [175, 180), [180, 185)
die absoluten und die relativen Klassenhäufigkeiten sowie die relativen
Summenhäufigkeiten.
b) Zeichnen Sie für die gruppierten Daten Histogramm, Häufigkeitspolygon,
Summenpolygon und empirische Verteilungsfunktion.
c) Kann die Textilfirma aufgrund der statistischen Erhebung auch weiterhin davon
ausgehen, ein Drittel ihrer Produktion für mindestens 175 cm herzustellen?
Aufgabe 16:
Berechnen und interpretieren Sie die Kenngrößen arithmetisches Mittel 𝑥̅ , Median 𝑥̃0,5 ,
Modalwert 𝑥𝑚𝑜𝑑 , Spannweite 𝑅̃ , Quartilsabstand 𝑥̃0,75 − 𝑥̃0,25, Streuung 𝑠 2 ,
Standardabweichung 𝑠, Variationskoeffizient 𝑣, Schiefe 𝑔1 und Exzess 𝑔2 für die
Einzeldaten aus Aufgabe 15.
Aufgabe 17:
Berechnen Sie, falls möglich, die in Aufgabe 16 genannten Parameter, zumindest jedoch
arithmetisches Mittel 𝑥̅𝑀 , Median 𝑥̃0,5 und Streuung 𝑠 2
a) für die gruppierten Daten der in Aufgabe A15 ermittelten Häufigkeitstabelle,
b) für die gruppierten Daten der in Aufgabe A14.
Aufgabe 18:
Eine Buslinie in einer Großstadt soll hinsichtlich ihrer Wirtschaftlichkeit auf der
Grundlage einiger statistischer Erhebungen analysiert werden. Wichtig dafür war die
Erfassung der Anzahlen 𝐻𝑗 von Fahrgästen innerhalb eines bestimmten Zeitraumen, die
den Bus über bestimmte Entfernungszonen 𝐾𝑗 , 𝑗 = 1, 2, . . . , 5 (Angaben in km)
benutzten. Sie sind in folgender Häufigkeitstabelle (Klassen, absolute
Klassenhäufigkeiten) zusammengestellt:
Entfernungszonen 𝐾𝑗 in km
[0, 5)
[5, 10)
[10, 15)
[15, 20)
[20, 25)
Anzahl der Fahrgäste 𝐻𝑗
15
32
46
22
5
a) Vervollständigen Sie die Häufigkeitstabelle mit den für die Lösung von b) und c)
erforderlichen Kenngrößen
b) Stellen Sie die empirische Verteilungsfunktion der Daten graphisch dar.
c) Berechnen und interpretieren Sie arithmetisches Mittel, Median und Modalwert
der Daten.
d) Welche Aussage über die Schiefe der Häufigkeitsverteilung lässt sich aus den
unter c) gewonnenen Parameter erhalten (ohne die Schiefe selbst zu
berechnen)?
Aufgabe 19:
Bei der Beobachtung der relativen Höhenstrahlungsintensität ergaben sich (für eine
geomagnetische Breite von 20° Nord) folgende Werte 𝐼𝑙 (𝑙 = 1, . . . , 15):
1,128
1,130
1,133
1,134
1,133
1,132
1,129
1,127
1,126
1,127
1,130
1,133
1,132
1,128
1,127
Man ermittle:
a)
b)
c)
d)
e)
f)
g)
∗
𝐼1∗ = 𝐼𝑚𝑖𝑛 ,
𝐼15
= 𝐼𝑚𝑎𝑥 ,
die zugehörige Variationsreihe,
die Spannweite,
das arithmetische Mittel,
die mittlere quadratische Abweichung,
den Variationskoeffizienten,
die konkrete empirische Verteilungsfunktion.
Aufgabe 20:
Die Druckfestigkeit (in MPa) von 40 Betonwürfeln mit 20 cm Kantenlänge wird
untersucht. Dabei ergab sich folgende Urliste:
24,5
24,8
24,3
23,6
21,8
26,4
29,2
18,9
25,5
21,8
24,9
12,5
16,9
16,1
26,1
13,5
25,1
20,8
18,3
12,0
21,8
17,4
21,4
16,8
19,2
17,4
12,9
25,1
23,9
33,3
20,5
19,7
9,9
20,5
23,1
30,9
19,0
19,0
16,9
26,9
a) Erstellen Sie die Häufigkeitstabelle.
Stellen Sie
b) das Histogramm
c) das Häufigkeitspolygon
d) das Summenpolygon
graphisch dar.
e) Mittels der Klasseneinteilung ermittle man die statistischen Maßzahlen 𝑥̅
(arithmetisches Mittel) und 𝑠 (empirische Standardabweichung).
Referenzen
Die in der Übung aufgeführten Aufgaben wurden folgenden Lehr- und Arbeitsbüchern
entnommen:
Beyer, O.; Hackel, H.; Pieper, V.; Tiedge, J.: Mathematik für Ingenieure,
Naturwissenschaftler, Ökonomen und Landwirte - Wahrscheinlichkeitsrechnung und
mathematische Statistik, Bd. 17, Leipzig: B.G. Teubner1985.
Böhm, P.: Induktive Statistik und Wahrscheinlichkeitsrechnung Arbeitsbuch II. Berlin:
Studeo Verlag 2004.
Böhm, P.; Ringhut, S.; Engler, S.; Deskriptive Statistik Arbeitsbuch II. Berlin: Studeo
Verlag 2004
Gillert, H.; Nollau, V.; Pieper, V.; Tiedge, J.: Mathematik für Ingenieure,
Naturwissenschaftler, Ökonomen und Landwirte – Übungsaufgaben zur
Wahrscheinlichkeitsrechnung und mathematische Statistik, Bd. Ü4, Leipzig: B.G.
Teubner1989.
Maibaum, G.: Wahrscheinlichkeitsrechnung. Frankfurt (Main): Harri Deutsch, 1980.
Menges, G.: Grundriß der Statistik – Teil 1: Theorie. Opladen: Westdeutscher Verlag
1972.
Nollau,V.; Patzsch, L.; Storm, R; Lange, C: Wahrscheinlichkeitsrechnung und Statistik in
Beispielen und Aufgaben. Stuttgart Leipzig: B.G. Teubner Verlagsgesellschft 1997
Vogel, F.: Beschreibende und schließende Statistik Aufgaben und Beispiele. München
Wien: Oldenbourg Wissenschaftsverlag 2001