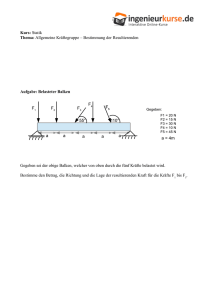
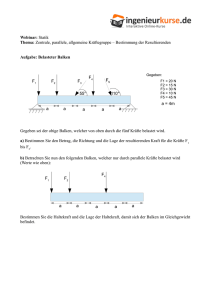
2 Kräfte und ihre Wirkungen
Werbung

5 2 Kräfte und ihre Wirkungen Kräfte treten überall auf – in der Natur, in der Technik, im Verkehr, im Sport, usw. Ein Getreidehalm wiegt sich im Wind, ebenso wie ein Fernsehturm. Bei Bewegungen sind im Allgemeinen Kräfte im Spiel. Das vielfach notwendige Verharren von Körpern in Ruhe wird ebenfalls durch Kräfte garantiert. Auch die Lösung der im Kapitel 1 dargestellten Fragestellungen erfordert eine intensive Beschäftigung mit der physikalischen Größe „Kraft“. Es gibt zahlreiche Möglichkeiten Kräfte einzuteilen. Kräfte können z. B. auftreten als • äußere Kräfte (wirkende Lasten), • Reaktionskräfte bzw. Auflagerkräfte, • innere Kräfte. Die Unterscheidung der Kräfte ist für das Lösen praktischer Fragestellungen der Statik von großer Wichtigkeit. Zunächst gilt es herauszufinden, welche Kräfte bei der gegebenen Problemstellung überhaupt wirksam sind. Die wirkenden Kräfte oder Lasten bezeichnet man als äußere Kräfte. Diese äußeren Kräfte rufen dann Lagerkräfte, Bodenreaktionskräfte, Gelenkkräfte und Kräfte, die zwischen Körpern oder Teilstrukturen wirken, hervor. Diese werden in der Statik zusammenfassend Reaktions- oder Auflagerkräfte genannt. Die äußeren Kräfte, das heißt die wirkenden Lasten, verursachen aber auch innere Kräfte in Strukturen und Bauteilen. Die inneren Kräfte gilt es zu ermitteln, um Informationen über die Belastbarkeit einer Struktur oder einer Teilstruktur zu erhalten. Dem Konstrukteur dienen sie unter anderem dazu, Bauteile sicher zu dimensionieren. 2.1 Äußere Kräfte, wirkende Lasten Äußere Kräfte treten bei bewegten und ruhenden Körpern auf. Eine stets wirkende Kraft ist die Gewichtskraft. Diese wird im Allgemeinen mit dem Formelzeichen G bezeichnet. Die Gewichtskraft errechnet sich aus der Masse m des Körpers und der Fall- oder Schwerebeschleunigung g mit der Formel G = m⋅ g (2.1), greift im Schwerpunkt des Körpers an und ist stets zum Erdmittelpunkt gerichtet, Bild 2-1. Die Gewichtskraft hat, wie jede andere Kraft, die physikalische Grundeinheit Newton, abgekürzt N. Größen, Dimensionen und Einheiten der Mechanik sind in Anhang A1 zusammengestellt. Bewegungen und insbesondere Bewegungsänderungen erfolgen unter dem Einfluss von Kräften. Bei Bewegungen treten neben der Gewichtskraft im Allgemeinen zusätzlich noch Beschleunigungs- oder Verzögerungskräfte auf. © Springer Fachmedien Wiesbaden 2016 H.A. Richard, M. Sander, Technische Mechanik. Statik, DOI 10.1007/978-3-658-14906-2_2 6 2 Kräfte und ihre Wirkungen Die Beschleunigungskraft FB errechnet sich aus der Masse m und der Beschleunigung a nach dem Grundgesetz der Mechanik: FB = m ⋅ a (2.2). Die Kraftrichtung entspricht der Richtung der Beschleunigung, Bild 2-1. Bild 2-1 Gewichtskraft G und Beschleunigungskraft FB beim Auto Bei Kreisbewegungen wirkt stets eine Fliehkraft. Sie errechnet sich aus der Masse m des Körpers auf der Kreisbahn, dem Radius r der Kreisbahn und der Winkelgeschwindigkeit ω mit der Formel FF = m ⋅ r ⋅ ω 2 (2.3). Die Fliehkraft wirkt bei der Kreisbewegung stets in radialer Richtung. Bild 2-2 Fliehkraft FF bei der Kreisbewegung einer Masse m Gewichtskraft, Beschleunigungskraft und Fliehkraft sind Massenkräfte, werden aber auch Volumenkräfte genannt, wobei sich die Masse m aus dem Volumen V und der Dichte ρ des Materials errechnet: m =V ⋅ρ (2.4). Massenkräfte wirken über das Volumen verteilt, werden jedoch idealisiert als im Schwerpunkt des Körpers angreifende Kräfte dargestellt, Bild 2-1 und Bild 2-2. Neben den Massen- bzw. Volumenkräften kommen als äußere Kräfte auch Flächenkräfte vor. Hierzu zählen z. B. der Luftwiderstand beim Auto oder die Windbelastung von Brücken und Gebäuden, die Schneelasten auf Dächern, der Wasserdruck auf die Staumauer eines Stausees und die Seitenwindkraft beim LKW, siehe auch Bild 2-3. 2.1 Äußere Kräfte, wirkende Lasten 7 Bild 2-3 Seitenwind bei einem LKW als Flächenkraft Die Flächenlast/-kraft wird in der Statik mit p bezeichnet und kann z. B. aus einer Kraft F und der Bezugsfläche A mit der Beziehung p= F A (2.5) errechnet werden. Die Einheit der Flächenlast ist damit z. B. N/m² oder N/mm², siehe Anhang A1. Neben Volumen- und Flächenlasten verwendet man in der Mechanik noch zwei wichtige Idealisierungen: • die Linienkraft und • die Punktkraft oder Einzelkraft. Die Linienlast q ist als Kraft pro Länge definiert und errechnet sich z. B. nach der Gleichung q= F l (2.6), wobei F die Kraft und l die Länge darstellt. Die Einheit ist z. B. N/m oder N/mm. Beispiele für die Linienkraft oder Streckenlast sind das Eigengewicht eines Balkens oder einer Rohrleitung, das über die Länge verteilt wirkt, siehe Bild 2-4. Auch die von einem Balken aufgenommene Flächenlast eines Deckenabschnitts eines Gebäudes oder eines Daches kann als Linien- oder Streckenlast angesehen werden. Bild 2-4 Gewicht eines Rohrleitungsteilstückes als Streckenlast Der Begriff Einzelkraft wird verwendet, wenn z. B. eine Kraftübertragung zwischen zwei Körpern auf kleiner, nahezu punktförmiger Berührungsfläche erfolgt oder wenn Massenkräfte und Flächenlasten idealisiert als Einzelkräfte betrachtet werden, die im Schwerpunkt der Massen oder der Flächen angreifen. Die Einheit der Einzelkraft F ist z. B. N oder kN. Diese Ideali- 8 2 Kräfte und ihre Wirkungen sierung ermöglicht den leichten Zugang zur Technischen Mechanik, insbesondere zur Statik, und erlaubt z. B. die Lösung aller Fragestellungen in Kapitel 1. Die Einzelkraft stellt einen Vektor dar. Zur Lösung der Fragestellungen der Statik können somit die Gesetzmäßigkeiten der Vektorrechnung herangezogen werden, siehe Anhang A2. Die Einzelkraft ist im Allgemeinen gekennzeichnet durch Größe, Richtung und Angriffspunkt. Bild 2-5 Zeichnerische Darstellung einer Einzelkraft Zeichnerisch wird die Einzelkraft als Pfeil (gerichtete Strecke, Vektor) dargestellt, Bild 2-5. Der Vektorcharakter wird durch den Pfeil über dem Buchstaben der physikalischen Größe deutlich: kennzeichnet Größe und Richtung der Einzelkraft, F F = F kennzeichnet den Betrag, das heißt die Größe der Einzelkraft. Für die zeichnerische Darstellung ist die Einführung eines Kräftemaßstabs wichtig. Das heißt, die dargestellte Länge der Kraft entspricht einer bestimmten Größe der Kraft. Zum Beispiel kann der Länge von 1 cm eine Kraft von 10 N entsprechen. In anderen Fällen kann der Kräftemaßstab 1 cm =ˆ 100 kN sinnvoll sein. Bei der Lösung technischer Fragestellungen (siehe auch Kapitel 1) wird häufig auf den Vektorpfeil über dem Formelzeichen verzichtet. Dies geschieht in der Regel dann, wenn die Kraftrichtung eindeutig bekannt ist (siehe auch Bild 2-1 und Bild 2-2). Der Kraftpfeil gibt in diesem Fall die Richtung der Kraft an, die Größe wird durch den Betrag bestimmt. Alle in diesem Abschnitt beschriebenen Kräfte können als äußere Kräfte oder wirkende Lasten bezeichnet werden. Sie rufen im Allgemeinen Reaktionskräfte an Aufstandsflächen oder Auflagern hervor und haben innere Kräfte in Tragstrukturen und Maschinen zur Folge. 2.2 Reaktionskräfte und innere Kräfte Reaktionskräfte sind z. B. die durch äußere Kräfte oder wirkende Lasten hervorgerufenen Stützkräfte oder Lagerreaktionen. Innere Kräfte werden ebenfalls durch die äußeren Kräfte verursacht. Die Zusammenhänge zwischen äußeren Kräften, Reaktionskräften und inneren Kräften sollen am Beispiel einer Lampe, die an einer Decke aufgehängt ist, verdeutlicht werden. 2.2 Reaktionskräfte und innere Kräfte 9 Bild 2-6 Verdeutlichung von äußerer Kraft, Reaktionskraft und innerer Kraft bei einer Lampe a) Darstellung als Gesamtsystem b) Im Schwerpunkt der Lampe wirkt die Gewichtskraft G = m·g als äußere Kraft c) Durch gedankliches Lösen des Seils vom Haken wird die Reaktionskraft R sichtbar d) Durch gedankliches Aufschneiden des Seils wird die Seilkraft S als innere Kraft erfahrbar In Bild 2-6a wird als Gesamtsystem ein Lampenkörper, der über eine Schnur mit einem Haken an der Decke befestigt ist, betrachtet. Die Masse des Lampenkörpers ist m, die Schnurmasse ist im Vergleich zur Masse des Lampenkörpers vernachlässigbar. Im Schwerpunkt des Lampenkörpers wirkt die Gewichtskraft G = m·g als äußere Kraft, Bild 2-6b. Die Hakenkraft R, Bild 2-6c, stellt die Reaktionskraft dar. Sie wird erst sichtbar durch das gedankliche Lösen des Seils vom Befestigungshaken. Dieses Vorgehen nennt man in der Mechanik „Freischneiden“. Dies bedeutet, das Teilsystem „Lampenkörper mit Schnur“ wird gedanklich vom Teilsystem „Haken und Decke“ gelöst. Die von dem Haken auf das Seil wirkende Kraft wird als Reaktionskraft R eingezeichnet. Mit den Methoden der Statik kann dann die Reaktionskraft ermittelt werden. Sie wirkt der Gewichtskraft entgegen, ist in diesem Fall aber betragsmäßig genauso groß wie die Gewichtskraft, also R = G . Natürlich muss auch die Schnur eine Kraft übertragen. Auch diese ist zunächst nicht zu erkennen. Sie wird erst durch das gedankliche Aufschneiden der Schnur als innere Kraft oder Schnur- bzw. Seilkraft S erfahrbar, Bild 2-6d. Um die Schnur auch nach dem Aufschneiden straff zu halten, muss jeweils am oberen und am unteren Schnurende eine betragsmäßig gleich große Schnurkraft S wirken. Diese innere Kraft S ist in dem betrachteten Fall betragsmäßig ebenso groß wie die Gewichtskraft, d. h. S = G . Dies wird durch Betrachtung des unteren Teilsystems in Bild 2-6d deutlich. Reaktionskräfte sind für die Auslegung von Lagerstellen wichtig. Die Kenntnis von inneren Kräften ist von Bedeutung für die Dimensionierung von Bauteilen und Strukturen. Daher zählt die Ermittlung von Reaktionskräften und inneren Kräften in Strukturen und Bauteilen zu den wichtigsten Aufgaben der Statik. 10 2 Kräfte und ihre Wirkungen 2.3 Kräfte am starren Körper Alle Körper in Natur und Technik sind verformbar. Die Verformungen von technischen Strukturen, die durch die Einwirkung von Kräften entstehen, sind im Allgemeinen jedoch klein gegenüber den Abmessungen dieser Konstruktionen. Die Lösung von Fragestellungen der Statik kann sehr vereinfacht werden, wenn man die Verformungen vernachlässigt, das heißt die Strukturen als starr betrachtet. Bild 2-7 a) Reale Brückenstruktur mit der Gewichtskraft im Schwerpunkt der Brücke b) Idealisierung der Brücke als starrer Körper mit den wirkenden Kräften und ihren Wirkungslinien Bei einem starren Körper können die Kräfte beliebig auf ihrer Wirkungslinie verschoben werden. Sie sind damit, anders als beim verformbaren Körper, nicht an ihren Angriffspunkt gebunden. Diese wichtige Idealisierung in der Statik ist somit eine wesentliche Hilfe bei der Lösung auch komplizierter Fragestellungen. Die Betrachtung der Kraftwirkungen am starren Körper nennt man auch Theorie 1. Ordnung. Dies bedeutet, z. B. für die Ermittlung der Auflagerreaktionen der Eisenbahnbrücke, Fragestellung 1-1, kann diese als starrer Körper betrachtet werden. Beim starren Körper kommt es auch nicht auf die Fachwerkstruktur an. Lediglich die Kräfte und ihre Wirkungslinien sind für die Bestimmung der Auflagerreaktionen von Bedeutung, Bild 2-7. Die Vernachlässigung der Verformungen ist im Allgemeinen ohne Bedeutung. 2.3 Kräfte am starren Körper 11 Sie führt nur bei Strukturen, die sich stark verformen, wie z. B. Bauteilen aus weichem Gummi, zu Fehlern. Die Idealisierung realer Strukturen als starre Körper erlaubt die Anwendung der nachfolgenden Axiome der Statik. Axiome sind Grundtatsachen, die durch die Erfahrung bestätigt werden. 2.3.1 Linienflüchtigkeitsaxiom Das Linienflüchtigkeitsaxiom lautet: „Der Angriffspunkt einer Kraft kann auf der Kraftwirkungslinie beliebig verschoben werden, ohne dass sich an der Wirkung auf den starren Körper etwas ändert.“ Das Axiom wird durch Bild 2-8 verdeutlicht. Die Kraft kann im Punkt A, im Punkt B oder an einem anderen Punkt der Wirkungslinie angreifen, die Wirkung auf den starren Körper ist stets dieselbe. Bild 2-8 Axiom von der Linienflüchtigkeit der Kraftvektoren Im Gegensatz zum starren Körper ist beim verformbaren Körper die Lage des Kraftangriffspunkts wesentlich, da die Verformungen des Körpers unter anderem vom Kraftangriffspunkt abhängen. Die Tatsache, dass man beim starren Körper die Kraft auf ihrer Wirkungslinie beliebig verschieben darf, bedeutet aber nicht, dass man die Kraft beliebig in der Ebene verschieben kann. Eine Parallelverschiebung zum Beispiel, ändert die Wirkung auf den Körper wesentlich. 2.3.2 Gleichgewichtsaxiom Dieses Axiom lautet: „Zwei Kräfte sind im Gleichgewicht, wenn sie • auf derselben Wirkungslinie liegen, • entgegengesetzt gerichtet und • gleich groß sind.“ Dies wird in Bild 2-9 verdeutlicht. Bild 2-9 Zwei Kräfte im Gleichgewicht 12 2 Kräfte und ihre Wirkungen Die Kräfteaddition ergibt (siehe auch A2): F1 + F2 = 0 (2.7). Gleichgewicht bedeutet somit, dass keine resultierende Kraft wirkt. Die Vektorsumme ergibt einen Nullvektor. Zwei Kräfte, die sich im Gleichgewicht befinden, bilden eine Gleichgewichtsgruppe. Ein ruhender Körper bleibt auch bei Einwirkung einer Gleichgewichtsgruppe in Ruhe. 2.3.3 Wechselwirkungsgesetz Dieses Axiom lässt sich wie folgt formulieren: „Die Kräfte, die zwei Körper aufeinander ausüben, sind gleich groß, entgegengesetzt gerichtet und liegen auf derselben Wirkungslinie.“ Dies bedeutet auch: „Die Wirkung ist stets der Gegenwirkung gleich“ oder „actio = reactio“. Da dieses Gesetz für das Verständnis der Technischen Mechanik insgesamt, aber auch der Statik von besonderer Wichtigkeit ist, soll es anhand von Beispielen noch weiter erläutert werden. Ein Stein, der zur Erde fällt, wird von der Erde angezogen. Auf den Stein wirkt die Gewichtskraft GS. Der Stein zieht aber in gleicher Weise auch die Erde an, Bild 2-10. Die Kraft FS wirkt auf derselben Wirkungslinie, ist gleich groß wie GS, aber entgegengesetzt gerichtet. Bild 2-10 Fallender Stein als Beispiel für das Wechselwirkungsgesetz Die Hand, die gegen eine Wand drückt, erfährt von der Wand eine gleich große Gegenkraft, Bild 2-11. Die Kraftwirkungen werden erst deutlich, wenn man die beiden Körper gedanklich trennt. Das heißt, die Körper müssen gedanklich „freigeschnitten“ werden. Dann sind die Kraftwirkungen auf jeden Körper zu betrachten: die Kraft, welche die Hand auf die Mauer ausübt und ebenso die Reaktionskraft, die von der Mauer auf die Hand wirkt. Die Gegenkraft FW liegt auf derselben Wirkungslinie wie die FH, ist betragsmäßig ebenso groß: FW = FH , aber ent Handkraft gegengesetzt gerichtet: FW = − FH . 2.3 Kräfte am starren Körper 13 Damit sind beide Kräfte auch im Gleichgewicht (siehe Gleichgewichtsaxiom). Bild 2-11 a) Hand drückt gegen eine Wand. b) „Freischnitt“ macht die wirkenden Kräfte sichtbar. Actio = Reactio wird auch bei der Lagerung der Eisenbahnbrücke in Bild 1-1 und in Bild 2-7 deutlich. Betrachtet man einmal das Auflager B im Freischnitt, so erkennt man, dass das Lager der Brücke eine Kraft FB auf das Betonteil ausübt, umgekehrt wirkt die Kraft FB aber auch als Lagerreaktionskraft FB auf die Brücke, Bild 2-12. Aktions- und Reaktionskraft liegen auf derselben Wirkungslinie, sind aber entgegengesetzt gerichtet. Bild 2-12 Aktions- und Reaktionskraft im Lager B der Eisenbahn– brücke 2.3.4 Axiom vom Kräfteparallelogramm Dieses Axiom lässt sich wie folgt formulieren: „Zwei Kräfte, die am selben Angriffspunkt angreifen, setzen sich zu einer Kraft zusammen, deren Größe und Richtung sich als Diagonale des von beiden Kräften aufgespannten Parallelogramms ergibt.“ Dieses Axiom beschreibt das Superpositionsprinzip der Kraftwirkungen, Bild 2-13. Das heißt, die resultierende Kraft R ersetzt die Kräfte F1 und F2 . Ebenso werden die Teilwirkungen von F1 und F2 durch die resultierende Wirkung von R ersetzt. 14 2 Kräfte und ihre Wirkungen Bild 2-13 Ermittlung der Resultierenden zweier Kräfte mit dem Kräfteparallelogramm Für die Zusammensetzung zweier Kräfte zu einer Resultierenden können auch die Gesetzmäßigkeiten der Vektoraddition herangezogen werden (siehe Anhang A2). Rechnerisch ergibt sich somit: F1 + F2 = R (2.8). Bild 2-14 zeigt die zeichnerische Darstellung der Addition der Kräfte F1 und F2 . Bild 2-14 Grafische Darstellung der Vektoraddition: Aus F1 und F2 wird die Resultierende R bestimmt. Die Anwendung des Axioms vom Kräfteparallelogramm soll an einem einfachen Beispiel verdeutlicht werden, bei dem zwei Kräfte an einem starren Körper angreifen. Durch die Richtungen der Kräfte sind die jeweiligen Wirkungslinien und der Schnittpunkt A R verschiebt man die Kräfte F1 vorgegeben, Bild 2-15a. Zur Ermittlung der Resultierenden und F2 auf ihren Wirkungslinien, so dass die Kräfte im Schnittpunkt A der Wirkungslinien angreifen (Linienflüchtigkeitsaxiom), Bild 2-15b. Die Resultierende und ihre Wirkungslinie ergibt sich dann aus dem Kräfteparallelogramm (Axiom vom Kräfteparallelogramm). 2.4 Zentrale ebene Kräftegruppe 15 Bild 2-15 Zwei Kräfte, die an einem starren Körper angreifen, können zu einer Resultierenden zusammengefasstwerden. A ihrer Wirkungslinien a) Kräfte F1 und F2 mit dem Schnittpunkt b) Ermittlung der Resultierenden R mit dem Kräfteparallelogramm 2.4 Zentrale ebene Kräftegruppe Zum leichteren Verständnis wird zunächst die ebene Statik betrachtet und dementsprechend die Wirkung von ebenen Kräftesystemen auf starre Körper sowie auf Bauteile und Strukturen untersucht. Von einer zentralen ebenen Kräftegruppe spricht man, wenn die Kräfte in einer Ebene liegen und sich alle Kraftwirkungslinien in einem Punkt schneiden. Wichtige Aufgaben der Statik sind dann die Ermittlung der Resultierenden einer Kräftegruppe, die Zerlegung einer Kraft nach verschiedenen Richtungen und die Betrachtung des Gleichgewichts dieser Kräftegruppe. 2.4.1 Ermittlung der Resultierenden Zwei Kräfte mit gemeinsamem Angriffspunkt lassen sich mit dem Axiom vom Kräfteparallelogramm, siehe Kapitel 2.3.4, zu einer Resultierenden zusammenfassen. Haben mehrere Kräfte – oder sogar beliebig viele Kräfte – einen gemeinsamen Angriffspunkt, das heißt, die Wirkungslinien aller Kräfte schneiden sich in diesem Punkt, so lassen auch diese sich zu einer Resultierenden zusammenfassen. Dazu bestehen mehrere Möglichkeiten: • Zeichnerische Ermittlung der Resultierenden mit dem Kräfteparallelogramm, • Zeichnerische Ermittlung der Resultierenden im Kräfteplan und • Rechnerische Ermittlung der Resultierenden. Auch wenn mehrere Kräfte wirken, kann das Axiom vom Kräfteparallelogramm zur Anwendung kommen. In diesem Fall werden schrittweise Teilresultierende ermittelt, so lange bis die Gesamtresultierende feststeht. Bild 2-16a zeigt eine zentrale Kräftegruppe mit den Kräften F1 , F2 und F3 , die an einer Konstruktion, hier idealisiert als starrer Körper dargestellt, angreifen. 16 2 Kräfte und ihre Wirkungen Bild 2-16 Zeichnerische Ermittlung der Resultierenden einer zentralen ebenen Kraftgruppe mittels Kräfteparallelogramm a) Zentrale Kräftegruppe mit den Kräften F1 , F2 und F3 b) Schrittweises Zusammensetzen nach dem Kräfteparallelogramm c) Resultierende R ersetzt die Wirkung der Einzelkräfte F1 , F2 und F3 Zunächst wird mit den Kräften F1 und F2 ein Kräfteparallelogramm gebildet und so die Teil resultierende R1,2 ermittelt. Diese Teilresultierende ergibt mit der Kraft F3 ein weiteres KräfR bestimmt werden kann, Bild 2-16b. teparallelogramm mit dem die Gesamtresultierende Von der Gesamtresultierenden R ist dann Größe, Richtung und Wirkungslinie bekannt. R 2.4 Zentrale ebene Kräftegruppe 17 ersetzt somit die Kraftwirkungen von F1 , F2 und F3 , Bild 2-16c. Dieses Verfahren kann auch bei mehr als 3 Kräften angewendet werden. Bild 2-17 Zeichnerische Ermittlung der Resultierenden einer zentralen ebenen Kräftegruppe im Kräfteplan a) Zentrale Kräftegruppe im Lageplan b) Aneinanderreihung der Kräfte im Kräfteplan ergibt die Resultierende R Die Resultierende einer zentralen Kräftegruppe kann zeichnerisch auch in einem so genannten Kräfteplan ermittelt werden. Die zentrale Kräftegruppe mit ihren Wirkungslinien wird zunächst in einem Lageplan dargestellt, Bild 2-17a. Der Lageplan gibt die geometrischen Zusammenhänge und die Lage der Kräfte zueinander maßstäblich wieder. Als Längenmaßstab (LM) kann z. B. 1 cm =ˆ 1 m verwendet werden. Dies bedeutet, 1 cm in der Zeichnung entspricht 1 m in der Realität. Überträgt man nun die Kräfte F1 , F2 und F3 in einen Kräfteplan, für den vorher ein bestimmter Kräftemaßstab (KM) festgelegt wurde, so lässt sich unmittelbar die Resultierende R ermitteln, Bild 2-17b. Detailliert ergibt sich folgendes Verfahren: und Richtung aus dem Lageplan in den Kräfteplan. An Zunächst überträgt man F1 nach Größe die Pfeilspitze von F1 trägt man F2 nach Größe und Richtung an, dann folgen F3 und eventuell noch weitere Kräfte. Die Verbindungslinie vom Anfangspunkt von F1 zur Pfeilspitze, der R nach Größe und Richtung. Die Richzuletzt eingetragenen Kraft, ergibt die Resultierende tung von R kann nun in den Lageplan zurück übertragen werden, so ist auch die Wirkungslinie von R bekannt. Zeichnerisch, aber auch rechnerisch bedeutet dies, die Vektorsumme einer ebenen Kräftegruppe ergibt die resultierende Kraft R , Bild 2-17b: n F1 + F2 + F3 + ... + Fn = Fi = R (2.9). i =1 Die analytische Ermittlung der Resultierenden lässt sich anhand von Bild 2-18 veranschaulichen. Dazu werden unter Verwendung eines x-y-Koordinatensystems alle Kräfte in Kompo nenten zerlegt. Jede Kraft lässt sich dann mit den Basisvektoren e x und e y wie folgt darstellen (siehe auch: Grundlagen der Vektorrechnung im Anhang A2): Fi = e x ⋅ Fix + e y ⋅ Fiy (2.10). 18 2 Kräfte und ihre Wirkungen Bild 2-18 Rechnerische Ermittlung der Resultierenden a) Zentrale Kräftegruppe im Lageplan b) Zerlegung der Kräfte in Komponenten im Kräfteplan Für die Kraftkomponenten gilt mit dem Winkel α i gegen die positive x-Achse: Fix = Fi ⋅ cos α i (2.11), Fiy = Fi ⋅ sin α i (2.12). Die Komponenten der Resultierenden ergeben sich dann aus der jeweiligen Summe der Kraftkomponenten in x- und y-Richtung: Rx = n Fix = i =1 Ry = n Fi ⋅ cos α i (2.13), i =1 n n i =1 i =1 Fiy = Fi ⋅ sin α i (2.14). Für das in Bild 2-18 dargestellte Beispiel bedeutet dies: R x = F1x + F2x + F3x (2.13), R y = F1y + F2y + (− F3y ) (2.14). Der Betrag der Resultierenden kann nun aus den Komponenten Rx und Ry ermittelt werden: R = R = Rx 2 + R y 2 (2.15), die Richtung der Resultierenden ergibt sich mit Ry Rx α R = arctan (2.16). 2.4 Zentrale ebene Kräftegruppe 19 Mit den Basisvektoren e x und e y ergibt sich die Resultierende wie folgt: R = ex ⋅ Rx + e y ⋅ Ry (2.17). Beispiel 2-1 Das in Bild 2-1 dargestellte Auto besitzt eine Masse m = 1000 kg, die Schwerebeschleunigung beträgt g = 9,81 m/s² und die Fahrbeschleunigung a = 2,5 m/s². Gesucht ist die resultierende Kraft R nach Größe und Richtung, die bei beschleunigter Bewegung auf das Fahrzeug einwirkt. Lösung: a) Ermittlung der wirkenden Kräfte G = m ⋅ g = 1000 kg ⋅ 9,81 FB = m ⋅ a = 1000 kg ⋅ 2,5 m s2 m s2 = 9810 N = 2500 N b) Zeichnerische Bestimmung der Resultierenden nach dem Kräfteparallelogramm Als Kräftemaßstab (KM) wird 1 cm =ˆ 2000 N gewählt. R und α können im Kräfteparallelogramm abgelesen werden. Im Rahmen der Zeichengenauigkeit ergibt sich: R = 10100 N β = 76° c) Berechnung der Resultierenden R = FB 2 + G 2 = β = arctan (9810 N )2 + (2500 N )2 9810 N G = arctan = 75,7° 2500 N FB = 10123 N 20 2 Kräfte und ihre Wirkungen Beispiel 2-2 Ein Funkmast wird durch mehrere Drahtseile gehalten. Je vier dieser Drahtseile sind mittels einer Halterung im Boden verankert. Wie groß ist die resultierende Kraft der Seile 1 bis 4 und in welche Richtung zeigt sie? 4 3 2 X geg.: S1 = 10 kN, S2 = 15 kN, S3 = 20 kN, S4 = 25 kN α = 30°, β = 20°, γ = 15°, δ = 10° δ γ 1 β α Lösung: a) Zeichnerische Bestimmung der Resultierenden mittels Kräfteparallelogramm R Durch schrittweises Zusammensetzen der Kräfte nach dem Kräfteparallelogramm erhält man: 10 kN R = 67,5 kN R 2,3 S4 S3 R 1,2 S2 S1 R2,3 R 1,2 2.4 Zentrale ebene Kräftegruppe 21 b) Zeichnerische Lösung mittels Kräfteplan Lageplan: Kräfteplan: Wirkungslinien der Kräfte S4 WL 3 WL4 10 kN WL 2 WL 1 y R S3 x S2 y R = 67,5 kN ε = 60° S1 ε x c) Rechnerische Lösung R = S1 + S 2 + S 3 + S 4 = S1x ⋅ e x + S1y ⋅ e y + S 2x ⋅ e x + S 2y ⋅ e y + S 3x ⋅ e x + S 3y ⋅ e y + S 4 x ⋅ e x + S 4 y ⋅ e y = (S1x + S 2 x + S 3x + S 4 x ) ⋅ e x + (S1y + S 2 y + S 3y + S 4 y ) ⋅ e y = Rx ⋅ e x + R y ⋅ e y Rx Ry R x = S1 ⋅ cos α + S 2 ⋅ cos(α + β ) + S 3 ⋅ cos(α + β + γ ) + S 4 ⋅ cos(α + β + γ + δ ) = 10 kN ⋅ cos 30° + 15 kN ⋅ cos 50° + 20 kN ⋅ cos 65° + 25 kN ⋅ cos 75° = 33,22 kN R y = S1 ⋅ sin α + S 2 ⋅ sin (α + β ) + S 3 ⋅ sin (α + β + γ ) + S 4 ⋅ sin (α + β + γ + δ ) = 10 kN ⋅ sin 30° + 15 kN ⋅ sin 50° + 20 kN ⋅ sin 65° + 25 kN ⋅ sin 75° = 58,46 kN R = 33,22 kN ⋅ e x + 58,76 kN ⋅ e y R= R = tan ε = Ry Rx (33,22 kN )2 + (58,76 kN )2 = = 67,51 kN 58,76 kN = 1,77 ε = 60,52° 33,22 kN 22 2 Kräfte und ihre Wirkungen 2.4.2 Zerlegung einer Kraft in verschiedene Richtungen Bei vielen Aufgaben der Statik ist es erforderlich, eine gegebene Kraft in statisch gleichwertige Kräfte nach verschiedenen Richtungen zu zerlegen. Bei einer zentralen Kräftegruppe ist eine Zerlegung nach zwei Richtungen eindeutig möglich, wenn die Wirkungslinie der zu zerlegenden Kraft durch den Schnittpunkt der beiden gegebenen Wirkungslinien geht. Bild 2-19 Zerlegung einer Kraft nach zwei nichtparallelen Richtungen a) Lageplan mit der zu zerlegenden Kraft F und den beiden gegebenen Wirkungslinien WL1 und WL2 b) Zerlegung einer Kraft F im Kräfteplan in die Kräfte F1 und F2 in die durch die Wirkungslinien WL 1 und WL2 vorgegebenen Richtungen c) Die Kräfte F 1 und F2 üben auf den starren Körper oder die untersuchte Struktur eine, der Kraft F gleichwertige Wirkung aus. Die Zerlegung der Kraft F nach zwei nichtparallelen Richtungen ist in Bild 2-19 dargestellt. Die Zerlegung erfolgt im Kräfteplan in die Richtungen der gegebenen Wirkungslinien WL1 dem gewählten Kräftemaßstab (KM) lassen sich die Beträge der KräfundWL2. Entsprechend te F1 und F2 aus dem Kräfteplan ablesen. Ebenso sind die Richtungen der Kräfte eindeutig bestimmt. Eine Zerlegung einer Kraft nach drei oder mehr Richtungen einer zentralen Kräftegruppe ist mit den Methoden der Statik nicht eindeutig möglich. Sie erfordert weitere Überlegungen und wird daher erst in einem anderen Teilgebiet der Mechanik, der Festigkeitslehre, betrachtet. 2.4 Zentrale ebene Kräftegruppe 23 Beispiel 2-3 Im Bereich des Lagers B der Fachwerk-Eisenbahnbrücke (Bild 1-1 und Bild 2-12) ist die Lagerkraft FB auf die Fachwerkstäbe 10 und 11 zu verteilen. Lösung: Lageplan: Kräfteplan: Wirkungslinie der Stabkraft 11 11 10 Wirkungslinie der Stabkraft 10 FB S11 B S10 FB Da Stäbe nur Kräfte in Stabrichtung übertragen können, sind die Wirkungslinien der Stabkräfte vorgegeben. Die Zerlegung der Auflagerkraft FB in die Stabkräfte S10 und S11 erfolgt dann im Kräfteplan. 2.4.3 Gleichgewicht dreier Kräfte “Drei Kräfte einer zentralen Kräftegruppe sind im Gleichgewicht, wenn • sie in einer Ebene liegen, • ihre Wirkungslinien sich in einem Punkt schneiden und • das Kräftedreieck sich schließt.“ Bild 2-20 a) Lageplan mit den Kräften F1 , F2 und F3 , deren Wirkungslinien sich in einem Punkt schneiden b) Geschlossenes Kräftedreieck 24 2 Kräfte und ihre Wirkungen Bei einem geschlossenen Kräftedreieck endet die Kraft F3 am Anfang von F1 , Bild 2-20. Das heißt, es existiert keine Resultierende. Rechnerisch ergibt sich: F1 + F2 + F3 = 0 (2.18). Wenn die Resultierende aller Kräfte, die auf einen Körper oder eine Struktur einwirken, null ist, verbleibt ein ruhender Körper in Ruhe, das heißt im Gleichgewicht. Dies ist eine wichtige Voraussetzung für alle nichtbewegten Tragstrukturen. Die Statik ist im Wesentlichen die Lehre vom Gleichgewicht. Beispiel 2-4 Der gezeichnete Träger, der bei A auf einer Rolle und bei B auf dem Mauerwerk aufgelagert ist, wird durch eine Kraft F belastet. Das Trägergewicht kann gegenüber F vernachlässigt werden. Man bestimme die Auflagerreaktionen bei A und B. F A B Lösung: Lageplan: Kräfteplan: Schnittpunkt aller Wirkungslinien LM C Wirkungslinie der Auflagerkraft B F A B Wirkungslinie der Auflagerkraft A a) Ermittlung aller Wirkungslinien im Lageplan Die Wirkungslinie von F ist durch den Kraftvektor gegeben. Die Rolle bei A kann keine horizontalen Kräfte übertragen, somit verläuft die Wirkungslinie vertikal. Beide Wirkungslinien schneiden sich im Punkt C. Um Gleichgewicht für den Träger zu sichern, muss die Wirkungslinie der Auflagerkraft bei B durch den Schnittpunkt C gehen (Gleichgewicht dreier Kräfte). 2.4 Zentrale ebene Kräftegruppe 25 b) Ermittlung der Auflagerkräfte im Kräfteplan Zunächst zeichnet man die Kraft F in einem geeigneten Kräftemaßstab in den Kräfteplan. Durch Übertragung der Richtungen der Wirkungslinien der Auflagerkräfte in den Kräfteplan erhält man ein geschlossenes Kraftdreieck und somit die Kräfte FA und FB nach Größe und Richtung. c) Freischnitt des Trägers mit äußerer Kraft und Reaktionskräften Die Auflagerkräfte kann man dann wieder in den Lageplan übertragen und erhält somit den komplett freigeschnittenen Träger, der sich bei Einwirkung aller Kräfte im Gleichgewicht befindet. F FA FB Auch bei der Lösung dieses Problems ist darauf zu achten, dass im Lageplan alle Längen entsprechend einem Längenmaßstab (LM) eingezeichnet werden und im Kräfteplan alle Kräfte einem Kräftemaßstab (KM) unterliegen. 2.4.4 Gleichgewichtsbedingungen für zentrale Kräftegruppe Bei einer zentralen Kräftegruppe mit drei oder auch mit mehr Kräften liegt Gleichgewicht vor, wenn die Summe aller Kräfte keine Resultierende ergibt, das heißt gleich null ist. Zeichnerisch liegt dann ein geschlossenes Krafteck vor, Bild 2-21. Bild 2-21 Gleichgewicht für zentrale Kräftegruppe 26 2 Kräfte und ihre Wirkungen Rechnerisch bedeutet dies: F1 + F2 + F3 + ... = 0 (2.19) oder allgemein n Fi = 0 (2.20). i =1 Summiert wird dabei über alle n Kräfte. Betrachtet man die Komponenten der Kräfte, so gelten die Komponentengleichungen: F1x + F2 x + F3x + ... = 0 F1y + F2 y + F3 y + ... = 0 (2.21), (2.22), oder allgemein n Fix = 0 → (2.23), Fiy = 0 ↑ (2.24). i =1 n i =1 Diese Formeln bezeichnet man als Gleichgewichtsbedingungen für eine zentrale ebene Kräftegruppe. Gleichgewicht liegt somit vor, wenn die Summe aller Kräfte in x-Richtung und die Summe aller Kräfte in y-Richtung jeweils null sind. Als Abkürzung für ΣFix = 0 wird häufig ein horizontaler Pfeil → und für ΣFiy = 0 ein vertikaler Pfeil ↑ verwendet. Dies ist deshalb sinnvoll, weil bei der Anwendung der Gleichgewichtsbedingungen die Richtung der Kräfte zu beachten ist. Die Pfeilrichtung kann dann als positive Richtung angesehen werden. Für Bild 2-21 gilt: 4 4 i =1 i =1 Fix = 0 und Fiy = 0 oder → F1x + F2 x − F3x − F4 x = 0 ↑ F1y − F2 y − F3y + F4 y = 0 (2.25), (2.26). Für den Fall, dass an dem Ring in Bild 2-21 mit den Kräften F1 , F2 , F3 und F4 gezogen wird, liegt dann Gleichgewicht vor, wenn die Gleichungen 2.25 und 2.26 erfüllt sind. 2.4 Zentrale ebene Kräftegruppe 27 Beispiel 2-5 An einem Kranhaken wird eine Last F = G über 2 Seile angehoben. Wie groß müssen die Seilkräfte S1 und S2 sein, damit Gleichgewicht herrscht? geg.: F = G = 2500 N, α = 30°, β = 40° Lösung: a) Zeichnerisch mit Lage- und Kräfteplan Lageplan: Kräfteplan: 500 N S2 α β F WL S 1 WLF WLS S1 2 Durch Ausmessen folgt: S1 = 1750 N, S2 = 1312,5 N b) Rechnerisch mit Gleichgewichtsbedingungen → − S1 ⋅ sin α + S 2 ⋅ sin β = 0 S1 = S 2 ⋅ ↑ F − S1 ⋅ cos α − S 2 ⋅ cos β = 0 sin β sin α (2) aus (1) und (2) folgt: F − S2 ⋅ S2 = F ⋅ sin β ⋅ cos α − S 2 ⋅ cos β = 0 sin α 1 1 = 2500 N ⋅ = 1330,2 N sin 40° ⋅ cos 30° sin β ⋅ cos α + cos β + cos 40° sin 30° sin α S1 = 1330,2 N ⋅ sin 40° = 1710,1 N sin 30° (1) 28 2 Kräfte und ihre Wirkungen 2.5 Beliebige ebene Kräftegruppe Bei einer beliebigen Kräftegruppe greifen die Kräfte verteilt an, d. h. nicht alle Wirkungslinien der Kräfte schneiden sich in einem Punkt. Von einer ebenen Kräftegruppe spricht man, wenn alle Kräfte, die auf einen Körper oder eine Struktur einwirken, sich in einer Ebene befinden. Bei den in Kapitel 1 formulierten Fragestellungen liegen jeweils beliebige ebene Kräftegruppen vor. Dies wird besonders deutlich bei Bild 1-2 bis Bild 1-5 sowie bei Bild 2-7, wo die Kraftwirkungslinien parallel liegen. Neben einer resultierenden Kraft R kann bei einer belie bigen Kräftegruppe auch ein resultierendes Moment M R (siehe Kapitel 3.2) auftreten. 2.5.1 Ermittlung der resultierenden Kraft einer ebenen Kräftegruppe Für die Ermittlung der resultierenden Kraft existieren verschiedene zeichnerische Methoden. Die Methode des schrittweisen Zusammensetzens nach dem Kräfteparallelogramm kann auch hier Anwendungen finden, wenn nicht alle Kräfte parallel sind und die Wirkungslinien zum Schnitt gebracht werden können. Dieses Vorgehen ist in Bild 2-22 gezeigt. Durch Anwendung des Linienflüchtigkeitsaxioms sowie des Axioms vom Kräfteparallelogramm für die Kräfte F1 und F2 erhält man die Teilresultierende R1,2 . Wählt man nun die gleiche Vorgehensweise für R1,2 und F3 , so erhält man die Gesamtresultierende R nach Größe, Richtung und Lage. Die Lage wird dabei durch die Wirkungslinie definiert. Bild 2-22 Ermittlung der Resultierenden einer ebenen Kräftegruppe durch schrittweises Zusammensetzen nach dem Kräfteparallelogramm Die Gesamtresultierende R kann auch durch Kräfteaddition im Kräfteplan ermittelt werden. Dazu zeichnet man alle wirkenden Kräfte in den Kräfteplan. Die Verbindungsstrecke zwischen dem Anfangspunkt von F1 und der zuletzt eingezeichneten Kraft ergibt die Resultierende nach Größe und Richtung, Bild 2-23. Die Lage der Resultierenden ergibt sich bei diesem Verfahren aber nicht. 2.5 Beliebige ebene Kräftegruppe 29 Bild 2-23 Ermittlung der Resultierenden durch Kräfteaddition im Kräfteplan Ein sehr allgemeingültiges grafisches Verfahren – das Seileckverfahren – erlaubt dagegen die Bestimmung von Größe, Richtung und Wirkungslinie der Resultierenden einer beliebigen Kräftegruppe. Bild 2-24 Ermittlung der Resultierenden einer beliebigen ebenen Kräftegruppe mit dem Seileckverfahren Dabei ergibt sich folgendes Vorgehen: Zunächst zeichnet man die Kräfte mit ihren Wirkungslinien in den Lageplan. Dann überträgt man die Kräfte in den Kräfteplan und ermittelt die Größe und die Richtung der Resultierenden R . Um die Lage der Resultierenden im Lageplan zu erhalten, ist nun das Seileckverfahren erforderlich. Dazu bestimmt man im Kräfteplan einen Pol P, dessen Lage beliebig ist, und verbindet Anfangs- und Endpunkte der Kräfte mit dem Pol durch so genannte Polstrahlen. Die Richtungen der Polstrahlen überträgt man dann in den Lageplan und zwar so, dass Seilstrahl 0 und Seil strahl 1 sich auf der Wirkungslinie der Kraft F1 schneiden (Punkt I). Diese Zuordnung im Lageplan entspricht der Zuordnung im Kräfteplan, wo die Kraft F1 und die Polstrahlen 0 und 1 ein geschlossenes Kräftedreieck bilden. Der Seilstrahl 1 schneidet dann die Wirkungslinie 30 2 Kräfte und ihre Wirkungen von F2 . Durch den Schnittpunkt II muss dann auch der Seilstrahl 2 verlaufen, usw. Zuletzt erhält man einen Schnittpunkt der Seilstrahlen 0 und 3, der in Bild 2-24 mit IV bezeichnet ist. Dieser Schnittpunkt stellt einen Punkt der Wirkungslinie der Resultierenden R dar. Die Rich tung der Resultierenden ist durch R selbst (siehe Kräfteplan) bestimmt. Das Verfahren heißt Seileck, weil sich ein zunächst lose hängendes Seil bei Belastung durch die Kräfte F1 , F2 und F3 in Form der Seilstrahlen (siehe Lageplan) spannen würde. Das Seileckverfahren funktioniert in gleicher Weise auch für parallele Kräfte. In diesem Fall würde allerdings der Pol P außerhalb des Kraftecks liegen (siehe Beispiel 2-6). Die rechnerische Ermittlung der Größe und der Richtung der Resultierenden erfolgt wie in 2.4.1 beschrieben. Die Lage der Resultierenden kann rechnerisch aber erst nach der Einführung des Momentenbegriffs (siehe Kapitel 3) ermittelt werden. Beispiel 2-6 Ein Balken ist durch vier vertikal wirkende Kräfte, F1 = 1,5 kN, F2 = 2,5 kN, F3 = 2 kN und F4 = 1,5 kN, belastet. Man bestimme die Größe und die Wirkungslinie der Resultierenden R. Lösung: Lageplan: 1m F2 F1 F3 Kräfteplan: 1 kN F4 F1 0 1,5 m 2m 1,5 m 2m 1,5 m F2 R 1 1 2 P 3 F3 2 0 3 4 4 F4 R x Mittels des Seileckverfahrens lässt sich die Größe und die Lage der Resultierenden ermitteln: R = 7,5 kN und x = 4,2 m Anmerkung: Da alle Kräfte vertikal wirken, kann auf den Vektorpfeil über F verzichtet werden. 2.5 Beliebige ebene Kräftegruppe 31 2.5.2 Zerlegung einer Kraft nach mehreren Richtungen Die Zerlegung einer Kraft nach zwei nichtparallelen Richtungen ist nur möglich, wenn die zu zerlegende Kraft durch den Schnittpunkt der beiden gegebenen Wirkungslinien geht (siehe 2.4.2, zentrale Kräftegruppe). Die Zerlegung einer Kraft nach zwei parallelen Richtungen kann nach dem Seileckverfahren vorgenommen werden. Bild 2-25 Zerlegung einer Kraft nach zwei parallelen Richtungen mit dem Seileckverfahren Zunächst wird das Seileckverfahren in der bekannten Weise (Abschnitt 2.5.1) angewandt. Man sucht einen Pol im Kräfteplan und überträgt die Polstrahlen 0 und 1 in den Lageplan, so dass sich die Seilstrahlen 0 und 1 auf der Wirkungslinie der zu zerlegenden Kraft F schneiden. Verbindet man nun die Schnittpunkte der Seilstrahlen mit den gegebenen Wirkungslinien, hier gekennzeichnet mit II und III, dann erhält man im Lageplan eine so genannte Schlusslinie s. Überträgt man die Richtung von s in den Kräfteplan, erhält man die gesuchten Kräfte F1 und F2. Die Zerlegung einer Kraft in drei nichtparallele Teilkräfte ist möglich, wenn sich die Wirkungslinien nicht in einem Punkt schneiden. Dann kann ein grafisches Verfahren nach CULMANN zur Anwendung kommen. Dabei ergibt sich folgendes Vorgehen (siehe Bild 2-26): Zunächst wird die zu zerlegende Kraft F mit einer der drei vorgegebenen Wirkungslinien zum Schnitt gebracht. Dann verbindet man diesen Schnittpunkt (z. B. Punkt I) mit dem Schnittpunkt der beiden anderen Wirkungslinien (z. B. Punkt II) zur CULMANNschen Gerade C. Im Kräfteplan erfolgt die Kräftezerlegung nun schrittweise. Zunächst wird die Kraft F in die Kraft F1 und die CULMANNsche Kraft C aufgeteilt: Dies geschieht entsprechend den Wir kungslinien im Punkt I im Lageplan. Dann wird die CULMANNsche Kraft C in die Kräfte F2 und F3 aufgeteilt, deren Wirkungslinien sich im Lageplan im Punkt II schneiden. 32 2 Kräfte und ihre Wirkungen Lageplan: Kräfteplan: Bild 2-26 Zerlegung einer Kraft nach drei nichtparallelen Richtungen mit dem CULMANN-Verfahren Eine Zerlegung einer Kraft nach mehr als drei Richtungen ist mit den Methoden der Statik unmöglich. Beispiel 2-7 *** 1,5a 1 2 a 3 Ein Hinweisschild mit einem Gewicht G ist, wie nebenstehend gezeichnet, an einer Hausmauer befestigt. Bestimmen Sie zeichnerisch die Kräfte in den Stäben 1, 2 und 3. geg.: G = 3 kN, a a G Zeichnerische Lösung: Da die Stäbe, mit denen das Schild an der Mauer befestigt ist, nur Zug- oder Druckkräfte in Stabrichtung aufnehmen können, ist die Lage der Wirkungslinien eindeutig definiert. Lageplan: Kräfteplan: a WL F2 WLF1 F3 1 2 C F2 1,5 kN C 3 WLF 3 WL G Durch Ausmessen folgt: F1 = 2,3 kN, F2 = 4,3 kN, F3 = 5,25 kN F1 G http://www.springer.com/978-3-658-14905-5