Webinar_Statik_allgemeine,zentrale,parallele Kräfte

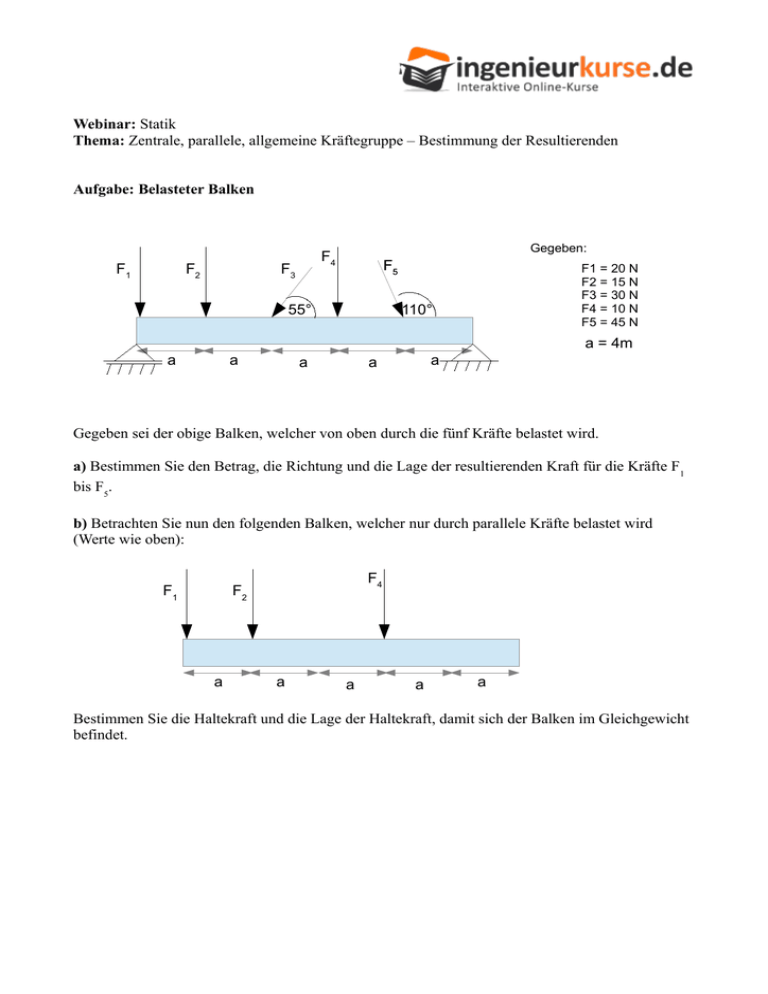
Webinar: Statik
Thema: Zentrale, parallele, allgemeine Kräftegruppe – Bestimmung der Resultierenden
Aufgabe: Belasteter Balken
F1
F2
Gegeben:
F4
F3
F5
55°
F1 = 20 N
F2 = 15 N
F3 = 30 N
F4 = 10 N
F5 = 45 N
110°
a = 4m
a
a
a
a
a
Gegeben sei der obige Balken, welcher von oben durch die fünf Kräfte belastet wird.
a) Bestimmen Sie den Betrag, die Richtung und die Lage der resultierenden Kraft für die Kräfte F1
bis F5.
b) Betrachten Sie nun den folgenden Balken, welcher nur durch parallele Kräfte belastet wird
(Werte wie oben):
F1
F4
F2
a
a
a
a
a
Bestimmen Sie die Haltekraft und die Lage der Haltekraft, damit sich der Balken im Gleichgewicht
befindet.
Verwendete Formeln:
Gleichgewichtsbedingungen:
∑ Fix = 0
∑ Fiy = 0
∑ Mx = 0
Kräftezerlegung:
y
y
F
F sin(α)
α
F cos(α)
x
x
Bestimmung der Resultierenden (gemeinsamer Angriffspunkt)
Teilresultierende in x-Richtung:
R x =∑ Fix
Teilresultierende in y-Richtung:
R y =∑ Fiy
Betrag der Resultierenden:
R= √ R 2x +R 2y
Richtung der Resultierenden:
tan (α)=
Ry
Rx
Winkel zwischen R und Rx
Bestimmung der Resultierenden (parallele Kräfte):
Betrag der Resultierenden:
R=∑ F
Richtung der Resultierenden
= Richtung der parallelen Kräfte
Lage der Resultierenden:
Arichimedisches Hebelgesetz
Bestimmung der Resultierenden (allgemeine Kräftegruppe):
Teilresultierende in x-Richtung:
R x =∑ Fix
Teilresultierende in y-Richtung:
R y =∑ Fiy
Betrag der Resultierenden:
R= √ R 2x +R 2y
Richtung der Resultierenden:
tan (α)=
Hebelarm der Resultierenden:
x
M
∑
h=
Ry
Rx
R
Winkel zwischen R und Rx
senkrechter Abstand vom gewählten
Bezugspunkt X
Trigonometrie am rechtwinkligen Dreieck:
sin (α)=
Hypotenuse
Gegenkathete
Gegenkathete
Hypotenuse
Ankathete
Hypotenuse
Gegenkathete
tan(α)=
Ankathete
cos(α)=
.
α
Ankathete