Statik - Forschungsbereich für Baumechanik und Baudynamik, TU
Werbung
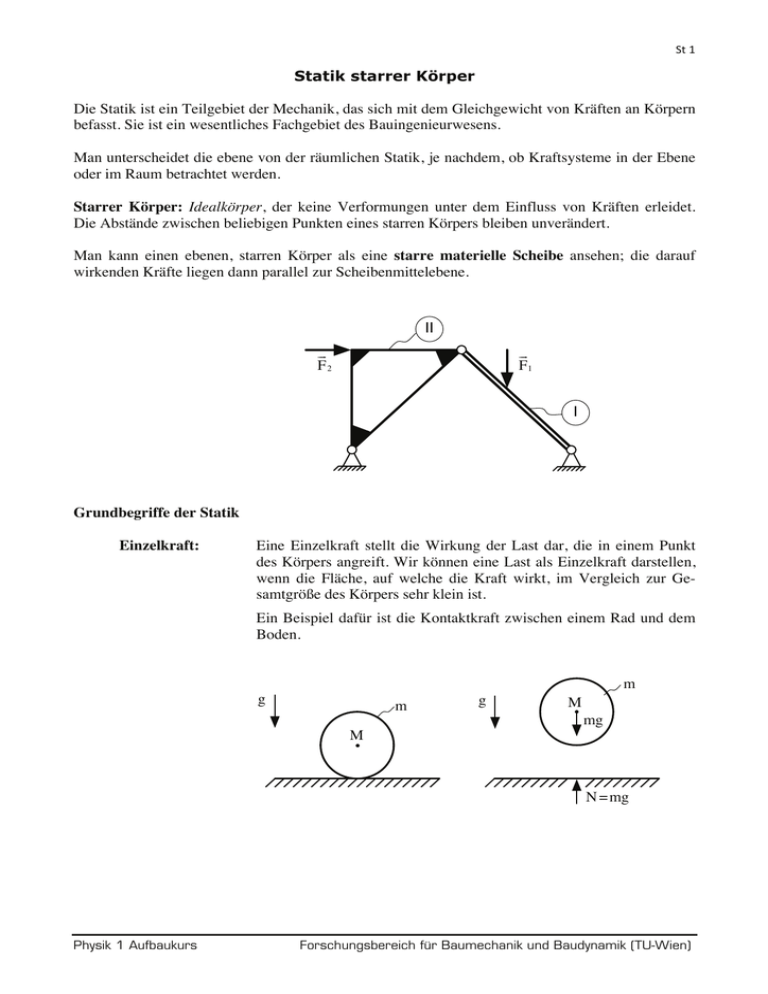
Statik starrer Körper Die Statik ist ein Teilgebiet der Mechanik, das sich mit dem Gleichgewicht von Kräften an Körpern befasst. Sie ist ein wesentliches Fachgebiet des Bauingenieurwesens. Man unterscheidet die ebene von der räumlichen Statik, je nachdem, ob Kraftsysteme in der Ebene oder im Raum betrachtet werden. Starrer Körper: Idealkörper, der keine Verformungen unter dem Einfluss von Kräften erleidet. Die Abstände zwischen beliebigen Punkten eines starren Körpers bleiben unverändert. Man kann einen ebenen, starren Körper als eine starre materielle Scheibe ansehen; die darauf wirkenden Kräfte liegen dann parallel zur Scheibenmittelebene. Ⅱ F2 F1 Ⅰ Grundbegriffe der Statik Einzelkraft: Eine Einzelkraft stellt die Wirkung der Last dar, die in einem Punkt des Körpers angreift. Wir können eine Last als Einzelkraft darstellen, wenn die Fläche, auf welche die Kraft wirkt, im Vergleich zur Gesamtgröße des Körpers sehr klein ist. Ein Beispiel dafür ist die Kontaktkraft zwischen einem Rad und dem Boden. m g m g M mg M N =mg Physik 1 Aufbaukurs Forschungsbereich für Baumechanik und Baudynamik (TU-Wien) Gleichgewicht: (zweier Kräfte) Zwei Kräfte sind im Gleichgewicht, wenn sie – auf derselben Wirkungslinie liegen – entgegengesetzt gerichtet und – gleich groß sind. F1 + F2 = 0 ⇒ F1 = − F2 ( F1 , F2 ) ... Gleichgewichtsgruppe F1 F2 starrer Körper dieselbe Wirkungslinie Wechselwirkung: (Schnittprinzip) Dies entspricht dem dritten Newtonschen Gesetz und besagt, dass zu jeder Kraft stets eine Gegenkraft auftritt. Axiom vom Kräfteparallelogramm: Physik 1 Aufbaukurs Beinhaltet die vektorielle Addition von Kräften (festgestellt auf Grund von Erfahrungstatsachen) Forschungsbereich für Baumechanik und Baudynamik (TU-Wien) Kräfte und Momente in der Ebene Die Wirkungslinien der betrachteten Kräfte und die ebenen starren Körper (Scheiben), an denen die Kräfte angreifen, liegen hier und im folgenden stets in einer Ebene (Zeichenebene, z.B. mit Kartesischem (x,y)-Koordinatensystem). Zeichnerische Zusammensetzung zentraler Kräfte: F1 F3 F1 F2 R F2 F3 starre Scheibe (a) Lageplan (b) Kräfteplan (mit Kräftemaßstab; z.B.: 1cm 1N ) R ... Resultierende F1 + F2 + F3 = R Analytische Zusammensetzung von (3 zentralen) Einzelkräften: y F1 F2 ey 0 ex F3 x F1 = F1x ex + F1y ey F2 = F2 x ex + F2 y ey F3 = F3x ex + F3y ey F1 + F2 + F3 = R , R = Rx ex + Ry ey F1x + F2 x + F3x = Rx F1y + F2 y + F3y = Ry Physik 1 Aufbaukurs Forschungsbereich für Baumechanik und Baudynamik (TU-Wien) Gleichgewicht zentraler Kräfte: Zentral wirkende Kräfte sind im Gleichgewicht, wenn – sie in einer Ebene liegen – ihre Wirkungslinien sich in einem Punkt schneiden – das zugehörige Kräftepolygon geschlossen ist. F3 starre Scheibe F3 F2 F1 F2 (a) Lageplan F1 (b) Kräfteplan (mit Kräftemaßstab) Wirken Einzelkräfte gemäß dem oberen Bild auf einen starren Körper, so bleibt dieser in Ruhe, d.h. er befindet sich im Gleichgewicht. Man bezeichnet ein System von Kräften, deren Wirkungslinien sich in einem Punkt schneiden, als zentrales Kraftsystem. Die (vektorielle) Gleichgewichtsbeziehung eines zentralen Kraftsystems lautet: n R = ∑ Fi = 0 i=1 Das Moment einer Einzelkraft: F = F e = Fx ex + Fy ey Fx = F cos α Fy = F sin α ⎡ x ⎤ ⎡ Fx ⎤ ⎡ 0 ⎥ ⎢ ⎢ ⎥ ⎢ 0 M (0) = (Fy x − Fx y)ez = r × F = ⎢ y ⎥ × ⎢ Fy ⎥ = ⎢ ⎢⎣ 0 ⎥⎦ ⎢ 0 ⎥ ⎢ Fy x − Fx y ⎣ ⎦ ⎣ A(x, y) ... Kraftangriffspunkt ⎤ ⎥ ⎥ ⎥ ⎦ M (0) ... Moment der Kraft F bezüglich des Bezugspunktes 0 r ... beliebiger Vektor vom Bezugspunkt 0 zur Wirkungslinie der Kraft F M (0) = (F l) ez l = x sin α − y cos α ... Hebelsarm (Normalabstand) Ausblick: Gleichgewicht eines allgemeinen Kraftsystems: n R = ∑ Fi = 0 i=1 Physik 1 Aufbaukurs und n M (0) = ∑ (ri × Fi ) = 0 i=1 Forschungsbereich für Baumechanik und Baudynamik (TU-Wien)