Enzym-Kinetik (Abb. 1) Das Thema der heutigen Vorlesung ist die

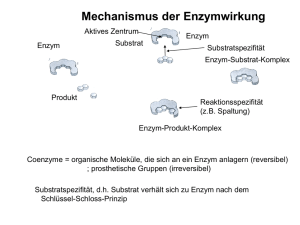
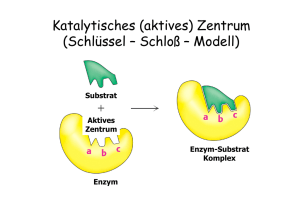
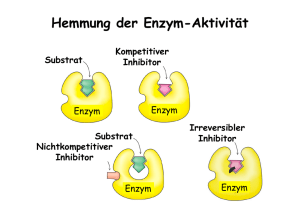
1
Enzym-Kinetik
(Abb. 1) Das Thema der heutigen Vorlesung ist die Kinetik isolierter und
gereinigter Enzyme zum Verständnis ihrer Reaktionsmechanismen. Wie ich schon
erwähnte, ist die Geschwindigkeit (V) einer monomolekularen, unkatalysierten
chemischen Reaktion proportional zu der Konzentration des Ausgangstoffes
(einklammerter S), und der Geschwindigkeitskonstante (k). Weil die gleichzeitige
Bestimmung der im Laufe der Reaktion fortlaufend sinkenden
Reaktionsgeschwindigkeit und der Konzentration des reagierenden Stoffes keine
einfache Aufgabe ist, beschäftigt sich die Reaktionskinetik im Allgemeinen mit der
Abhängigkeit der Anfangsgeschwindigkeit der Reaktion (V0) von der anfänglichen
Konzentration des reagierenden Stoffes (einklammerter S), die man kennt, und in
einer Versuchsserie nach Belieben variieren kann. In einem Koordinatensystem bei
dem die Abszissenachse die anfängliche Konzentration des Ausgangstoffes, und
die Ordinatenachse die Anfangsgeschwindigkeit der Reaktion repräsentieren,
erscheint die betreffende Gleichung als eine, aus dem Origo ausgehende Gerade,
deren Steigung mit dem Wert der Geschwindigkeitskonstante der Reaktion
übereinstimmt.
Es stellte sich aber heraus, dass bei enzymatischen Reaktionen dies nicht der
Fall ist. Zwar wird die Anfangsgeschwindigkeit (V0) immer größer und größer
während man die anfängliche Substratkonzentration erhöht, aber nicht nach einer
Gerade, sondern nach einer als Sättigungskurve bezeichnete Hyperbole. Je größer
die Anfangskonzentration des Substrats ist desto weniger kann ihre weitere
Erhöhung die Anfangsgeschwindigkeit weiter erhöhen. Schließlich wird eine
maximale Anfangsgeschwindigkeit (Vmax) erreicht. Später werden sie sehen, dass
die maximale Anfangsgeschwindigkeit bei enzymkinetischer Analyse des
Mechanismus von enzymatischen Reaktionen ein wichtiger Faktor ist.
2
Aus der Analyse solcher Kurven wurde festgestellt, dass die
Anfangsgeschwindigkeit der mit blauer Farbe dargestellten dreiphasigen
monomolekularen enzymatischen Reaktion nicht zu der Substratkonzentration
proportional ist, sondern zu der Konzentration des Enzym-Produkt-Komplexes
[EP], und die partiale Geschwindigkeitskonstante seiner Spaltung (k3) stimmt mit
der Geschwindigkeitskonstante der Gesamtreaktion überein.
Im Allgemeinen kann man die folgenden feststellen: Erstens, die
Gesamtgeschwindigkeit einer enzymatischen Reaktion ist immer zu der
Konzentration desjenigen Zwischenprodukts proportional, dessen Weiteränderung
am langsamsten ist. In der allgemeinen Reaktionsgeschwindigkeit-Gleichung ist die
Konzentration des geschwindigkeitsbestimmenden Zwischenprodukts mit [Zg]
symbolisiert. Zweitens, die Geschwindigkeitskonstante der langsamsten
Weiteränderung stimmt mit der Geschwindigkeitskonstante der Gesamtreaktion
überein. Diese ist in der rotfarbigen Gleichung der allgemeinen
Reaktionsgeschwindigkeit mit kkat symbolisiert.
Weiterhin stellte es sich heraus, dass diese Feststellungen für eine relativ
lange Zeit gelten, abgesehen von einer unmessbar kurzen Anfangsperiode, in der
das Enzym mit dem Substrat gesättigt wird. Nach der Anfangsperiode stellt
nämlich für eine relativ lange Zeit ein dynamisches Gleichgewicht zwischen der
Entstehung und der Weiteränderung des Geschwindigkeit-bestimmenden
Zwischenprodukts ein, das auf Deutsch als Fliessgleichgewicht, auf Englisch als
"steady state" bezeichnet ist. Während der Fliessgleichgewicht-Periode bleibt die
Konzentration aller Zwischenprodukte konstant, auch die Konzentration des
Geschwindigkeit-bestimmenden Zwischenprodukts. Daher bleibt die
Geschwindigkeit der Gesamtreaktion während der Fliessgleichgewicht-Periode
konstant, und gleich der Anfangsgeschwindigkeit.
3
(Abb. 2) Die experimentelle Bestimmung der Konzentration des
Geschwindigkeit-bestimmenden Zwischenprodukts ist im Algemeinen eine
schwierige Aufgabe, manchmal kann es gar nicht verwirklicht werden. Deshalb
leiteten Michaelis und Menten eine Gleichung ein, die nur bekannte oder einfach
messbare Faktoren wie die Anfangsgeschwindigkeit, V0, die maximale
Anfangsgeschwindigkeit, Vmax, die anfängliche Substratkonzentration
eingeklammerter [S], und die so genannte Michaelis-Konstante Km enthält. Diese
Konstante ist eine Kombination der partialen Geschwindigkeitskonstanten der
einzelnen Phasen der enzymatischen Reaktionen. Bei der dargestellten
monomolekularen, zweiphasigen, enzymatischen Reaktion ist die MichaelisKonstante gleich k2 plus k-1 per k1. Der Wert der Michaelis-Konstante variiert sich
erheblich von Enzym zu Enzym wie in der projizierten Tabelle zu sehen ist.
Wenn man den Ausdruck, V0 gleich Vmax/2, in die Michaelis-MentenGleichung einsetzt, bekommt man nach Vereinfachung und Umänderung, dass die
Michaelis-Konstante, Km, gleich derjenigen Substrat-Konzentration ist, bei der die
Anfangsgeschwindigkeit (V0) genau die Hälfte der maximalen Anfangsgeschwindigkeit (Vmax) ist. Bei sehr niedrigen Substratkonzentrationen, wobei die
Michaelis-Konstante viel größer als sie ist, kann sie in dem Nenner der MichaelisMenten-Gleichung vernachlässigt werden. So ergibt sich anstatt der
hyperbolischen Sättigungskurve eine lineare Abhängigkeit der
Anfangsgeschwindigkeit von der Substratkonzentration mit einer Steigung von
Vmax/Km. Bei sehr hohen Substrat-Konzentrationen, wobei die Michaelis-Konstante
viel kleiner als sie ist, kann die Michaelis-Konstante in der Michaelis-MentenGleichung vernachlässigt werden. So ergibt sich nach Vereinfachung, dass die
Anfangsgeschwindigkeit, unabhängig von der Veränderung der
Substratkonzentration, immer gleich Vmax ist. Mit der Ausnahme der
4
regulatorischen Enzyme, die später diskutiert werden, gehorchen alle Enzyme der
Michaelis-Menten-Kinetik, unabhängig von ihren Mechanismen.
(Abb. 3) Damit die Michaelis-Menten-Gleichung für die Praxis einfacher
verwendet werden kann, wird sie verschiedenartig transformiert. Die am häufigsten
verwendete Transformation besteht in der Inversion ihrer beiden Seiten. Nach
Umformung und Vereinfachung erhält man die so genannte Lineweaver-BurkGleichung. Wenn man diese Gleichung in einem Koordinatensystem darstellt,
dessen Abszissenachse den Kehrwert der anfänglichen Substratkonzentration und
die Ordinatenachse den Kehrwert der Anfangsgeschwindigkeit repräsentieren,
bekommt man eine Gerade. Die Steigung dieser Gerade ist Km /Vmax, sie schneidet
die Ordinatenachse bei 1/Vmax und die Abszissenachse bei -1/Km.
Die Lineweaver-Burk-Gerade einer beliebigen enzymatischen Reaktion kann
experimentell folgenderweise aufgenommen werden. Man bestimmt die
Anfangsgeschwindigkeit der fraglichen enzymatischen Reaktion bei zwei,
voneinander weit liegenden Substratkonzentrationen. Danach zeichnet man die
Kehrwerte der gemessenen Anfangsgeschwindigkeiten gegen die Kehrwerten der
entsprechenden Substratkonzentrationen in das Lineweaver-BurkKoordinatensystem ein, und zieht eine Gerade durch diese zwei Punkte. Die
Kehrwerte der Michaelis-Konstante und der maximalen Anfangsgeschwindigkeit
können Sie von dem bekommenen Diagramm ablesen.
(Abb. 4) Erinnern Sie sich daran, dass die Anfangsgeschwindigkeit
irgendeiner enzymatischen Reaktion zu der Konzentration des Geschwindigkeitbestimmendes Zwischenprodukts [eingeklammerter Zg] und der allgemeinen
Geschwindigkeit-Konstante (kkat) proportional ist. Es wurde auch diskutiert, dass
im Falle von großem Substratüberschuss die Anfangsgeschwindigkeit mit der
maximalen Anfangsgeschwindigkeit, Vmax, übereinstimmt. Darüber hinaus ist bei
großem Substratüberschuss das Enzym mit dem Geschwindigkeit-bestimmenden
5
Zwischenprodukt gesättigt, daher ist Konzentration des Enzyms eingeklammerter
[Et] mit der Konzentration dieses Zwischenprodukts gleich. Mit Berücksichtigung
der so bekommenen schwarzen Gleichungen umwandelt sich die allgemeine
Reaktionsgeschwindigkeit-Gleichung zu Vmax gleich mit kkat multiplizierter
Enzymkonzentration ist. Setzt man dies in die Michaelis-Menten-Gleichung ein,
bekommt man die blaue Gleichung und nach Umformung die braune Gleichung.
Mit Hilfe dieser Gleichung kann man den Wert der Geschwindigkeitskonstante der
allgemeinen Reaktionsgeschwindigkeit-Gleichung ausrechnen, wenn man die
Anfangsgeschwindigkeit bei einer bekannten, großen Substratkonzentration
bestimmt, und die Enzymkonzentration und den Wert der Michaelis-Konstante
kennt.
Diese Geschwindigkeitskonstante wird als Wechselzahl, auf English
"turnover number" bezeichnet. Sie ist gleich derjenigen Zahl der der
Substratmoleküle, die in einer Sekunde von einem einzigen Enzymmolekül zu
Produktmolekülen überführt werden können, wenn das Enzym mit dem Substrat
gesättigt ist. Die Wechselzahl variiert von einem Enzym zu dem anderen erheblich.
Ein einziges Katalase-Molekül kann zum Beispiel 40 Millionen
Wasserstoffperoxyd-Moleküle in einer Sekunde zu Sauerstoff-Molekülen und
Wassermolekülen zersetzen. Dies ist eine unglaublich große Zahl. Dagegen
hydrolysiert ein Molekül eine Art ATP-ase nur 0.4 ATP-Moleküle in einer
Sekunde.
Der beste Parameter für den Vergleich der katalytischen Wirksamkeit von
unterschiedlichen Enzymen ist das Verhältnis ihrer kkat und Km Werte. Dieses
Verhältnis kann für eine beliebige enzymatische Reaktion mit einem Experiment
bestimmt werden, in dem man die Anfangsgeschwindigkeit bei einer bekannten,
sehr niedrigen Substratkonzentration bestimmt. In diesem Fall kann nämlich die
Substratkonzentration im Nenner der blaufarbigen Gleichung vernachlässigt
6
werden. Dadurch umändert sich diese Gleichung zu der grünfarbigen Gleichung, in
der sowohl die Anfangsgeschwindigkeit, als auch die Konzentrationen vom
Substrat und Enzym bekannt sind.
Für den Vergleich-Parameter kkat/Km existiert ein oberer Grenzwert zwischen
108 und 109, der von derjenigen Geschwindigkeit bestimmt wird, mit der die
Substratmoleküle in wässriger Lösung durch Diffusion die Enzymmoleküle
erreichen. Enzyme, deren kkat/Km Werte in der Nähe dieses Grenzwertes liegen,
umändern die durch Diffusion zu ihnen gelieferten Substratmoleküle sofort zu
Produktmolekülen. Solche Enzyme nennen wir katalytisch perfekt. Wie Sie an der
projizierten Tabelle ablesen können, erreichen Enzyme mit sehr unterschiedlichen
kkat und Km Werten beinahe diesen Grenzwert.
(Abb. 5) In bimolekularen enzymatischen Reaktionen bindet jedes
Enzymmolekül zwei Substratmoleküle, wie Hexokinase ein ATP-Molekül und ein
D-Glucose-Molekül bei der bereits erwähnten Bildung von D-Glucose-6-Phosphat.
Je nach der Reihenfolge der Substratsbindung können bimolekulare enzymatische
Reaktionen auf unterschiedlichen Wegen fortschreiten. Auf dem Weg mit
zufälliger Reihenfolge werden beide Substrate, S1 und S2, von dem Enzym mit
ähnlicher Wahrscheinlichkeit reversibel gebunden. Dann kann die reversible
Bindung des anderen Substrats erfolgen, unter Bildung eines ternären EnzymSubstrat-1-Substrat-2-Komplexes, ES1S2. Schließlich zerfällt dieser Komplex zu
dem Enzym und den beiden Produkten.
Auf dem Weg mit geordneter Reihenfolge kann das Enzym nur Substrat-1
binden, Substrat-2 aber nicht. Der Enzym-Substrat-1-Komplex kann danach
Substrat-2 binden, der entstehende ternäre Enzym-Substrat-1-Substrat-2-Komplex
spaltet sich schließlich zu dem Enzym und den Produkten.
Bei der geordneten Reihenfolge gibt es einen Reaktionsweg ohne die
Bildung eines ternären Enzym-Substrat-1-Substrat-2-Komplexes. Bei einer solchen
7
bimolekularen Reaktion umändert sich der Enzym-Substrat-1-Komplex zu einem
Enzym-Produkt-1-Komplex, in dem das Enzym eine persistente Veränderung
erträgt. Dieser Komplex zerfällt dann zu Produkt-1 und dem veränderten Enzym,
das nur Substrat-2 binden kann, Substrat-1 aber nicht mehr. Schließlich zerfällt der
Enzym-Produkt-2-Komplex zu Produkt-2 und dem originalen Enzym.
Es kann vorkommen, dass die persistente Veränderung des Enzyms darin
besteht, dass ihm Substrat-1 bei seiner Umwandlung zu Produkt-1 eine funktionelle
Gruppe überträgt. Das so veränderte Enzym seinerseits überträgt diese funktionelle
Gruppe an Produkt-2 bei dem Zerfall des Enzym-Substrat-2-Komplexes. Man
bezeichnet einen solchen Reaktionsverlauf als Ping-Pong-Mechanismus.
Ob bei einer bimolekularen enzymatischen Reaktion ein ternärer EnzymSubstrat-1-Substrat-2-Komplex entsteht, kann man mit der folgenden
Versuchsserie ermitteln. Bei Konstanthalten der Enzymkonzentration und der
Konzentration von Substrat-2, verändert man die Konzentration von Substrat-1,
und bestimmt die dadurch erzeugte Veränderung der Anfangsgeschwindigkeit.
Dieser Vorgang wird danach bei drei anderen Konzentrationen von Substrat-2
wiederholt. Bei der doppeltreziproken Darstellung der bekommenen Ergebnisse
erhält man 4 Geraden. Wenn sie sich in einem gemeinsamen Punkt schneiden, so
handelt es sich um die Entstehung eines ternären Enzym-Substrat-Komplexes.
Parallele Geraden weisen auf einen Ping-Pong-Mechanismus hin.
(Abb. 6) Weitere Informationen zur Aufklärung des Mechanismus
enzymatischer Reaktionen kann man durch Analyse des Einflusses von EnzymInhibitoren auf ihre Kinetik bekommen. Enzymatische Inhibition, die häufig als
enzymatische Hemmung bezeichnet ist, hat zwei Klassen: reversible und
irreversible. Reversible Inhibition ihrerseits kann kompetitiv, unkompetitiv oder
gemischt sein.
8
Der chemische Aufbau und die räumliche Anordnung eines reversiblen,
kompetitiven Inhibitors ist denen des Substrats ähnlich. Deshalb konkurriert der
Inhibitor mit dem Substrat um das aktive Zentrum des Enzyms. Eine Anzahl der
Enzym-Moleküle bilden mit Inhibitor-Molekülen im Rahmen eines dynamischen
Gleichgewichts Enzym-Inhibitor-Komplexe. Während ihrer Lebenszeit kann ihr
Enzym-Teil mit dem Substrat nicht reagieren. Dadurch wird die Konzentration des
funktionsfähigen Enzyms gesenkt und die enzymatische Reaktion verlangsamt.
Es wurde theoretisch abgeleitet, und experimentell bewiesen, dass die
Michaelis-Menten-Gleichung für die reversible, kompetitive Inhibition die
blaufarbige Gestalt annimmt, in der im Vergleich mit der originalen Gleichung die
Michaelis-Konstante der nicht-inhibierten Reaktion mit einem Faktor (α)
multipliziert wird. Wie man von der für diesen Fall geltenden Lineweaver-BurkGleichung ablesen kann, ist der Kehrwert von Vmax unabhängig von dem Faktor α;
das Km/Vmax Verhältnis, das heisst die Steigung der Lineweaver-Burk-Gerade ist
aber mit α multipliziert.
Die mit α multiplizierte Michaelis-Konstante ist als scheinbare MichaelisKonstante bezeichnet. Bei großem Substratüberschuss ist die Substratkonzentration
viel größer als die scheinbare Michaelis-Konstante, die daher in dem Nenner der
umgestalteten Michaelis-Menten-Gleichung vernachlässigt werden kann. So ergibt
sich nach Vereinfachung, dass die Anfangsgeschwindigkeit bei großer
Substratkonzentration gleich der maximalen Anfangsgeschwindigkeit (Vmax) ist.
Ob eine Enzym-Inhibition reversibel und kompetitiv ist, kann man mit dem
folgenden Experiment ermitteln. Man nimmt das Lineweaver-Burk-Diagramm
einerseits ohne den Inhibitor, andererseits mit zwei unterschiedlichen InhibitorKonzentrationen auf, unter Konstanthaltung der Enzymkonzentration. Bei
kompetitiver, reversibler Enzym-Inhibition besitzen die drei bekommenen Geraden
unterschiedliche Steigungen, und schneiden sich im gleichen Punkt, der an der
9
Ordinatenachse liegt. Man kann den Wert von α bei einer reversibel und kompetitiv
inhibierten, enzymatischen Reaktion dadurch ausrechnen, dass man die Steigung
ihrer Lineweaver-Burk-Gerade mit der Steigung der Lineweaver-Burk-Gerade der
nicht-inhibierten Reaktion dividiert.
(Abb. 7) Der chemische Aufbau eines reversiblen und unkompetitiven
Inhibitors ähnelt dem chemischen Aufbau des Substrats nicht. Daher kann er sich
an das aktive Zentrum des Enzyms nicht binden, besitzt aber eine eigene
Bindungsstelle an dem Enzym. Trotzdem kann er sich an das substratfreie Enzym
nicht binden, sondern nur an einem Enzym-Substrat-Komplex. Der entstehende
Enzym-Substrat-Inhibitor-Komplex verhindert für seine Lebenszeit die
Umwandlung des Substrats zu Produkt, und dadurch verlangsamt die Reaktion.
Es wurde theoretisch abgeleitet und experimentell bewiesen, dass die
Michaelis-Menten-Gleichung für die reversible, unkompetitive Inhibition die
blaufarbige Gestalt annimmt, in der die Konzentration des Substrats in dem Nenner
der Gleichung mit einem Faktor, markiertem α', multipliziert ist. Wie man an der
für diesen Fall geltenden Lineweaver-Burk-Gleichung ablesen kann, ist das
Km/Vmax Verhältnis, das heisst die Steigung der Lineweaver-Burk-Gerade
unabhängig von markiertem α', der Kehrwert von Vmax ist aber mit ihm
multipliziert.
Die mit markiertem α' multiplizierte Substratkonzentration ist als scheinbare
Substratkonzentration bezeichnet. Bei großem Substratüberschuss ist die
scheinbare Substratkonzentration viel größer als die Michaelis-Konstante; sie kann
daher in dem Nenner der umgestalteten Michaelis-Menten-Gleichung
vernachlässigt werden. So ergibt sich nach Vereinfachung, dass die
Anfangsgeschwindigkeit bei großem Substrat-Überschuss gleich der maximalen
Anfangsgeschwindigkeit per markiertem α' ist.
10
Ob eine Enzym-Inhibition reversibel und unkompetitiv ist, kann mit dem
folgenden Experiment ermittelt werden. Man nimmt das Lineweaver-BurkDiagramm einerseits ohne den Inhibitor, andererseits mit zwei unterschiedlichen
Inhibitor-Konzentrationen, unter Konstanthaltung der Enzymkonzentration auf.
Wenn man drei Geraden mit gleicher Steigung bekommt, die sowohl die
Ordinatenachse als auch die Abszissenachse in unterschiedlichen Punkten
schneiden, handelt es sich um eine unkompetitive, reversible Inhibition. Erinnern
Sie sich daran, dass bei der kompetitiven, reversiblen Inhibition die entsprechenden
Geraden unterschiedliche Steigungen haben. Man kann den Wert von markiertem
α' einer reversibel und unkompetitiv inhibierten Reaktion dadurch ausrechnen, dass
man den Ordinatenwert des Punktes wo ihre Lineweaver-Burk-Gerade die
Ordinatenachse schneidet mit dem Ordinatenwert desjenigen Punktes dividiert, wo
die Lineweaver-Burk-Gerade der nicht-inhibierten Reaktion die Ordinatenachse
schneidet.
(Abb. 8) In Ähnlichkeit mit einem reversiblen unkompetitiven Inhibitor
besitzt ein reversibler, gemischter Inhibitor eine eigene Bindungsstelle an das
Enzym. In Gegenteil zu einem reversiblen, unkompetitiven Inhibitor kann sich ein
reversibel, gemischter Inhibitor sowohl an den Enzym-Substrat-Komplex unter
Bildung eines ternären Enzym-Substrat-Inhibitor-Komplexes, als auch an das
substratfreies Enzym unter Bildung eines Enzym-Inhibitor-Komplexes binden.
Dieser Komplex kann dann entweder zu Enzym und Inhibitor zerfallen, oder durch
Anbindung eines Substratmoleküls zu dem Enzym-Substrat-Inhibitor-Komplex
umändern. So entsteht ein Enzym-Substrat-Inhibitor-Kreislauf, mit einem Ausgang
in Richtung der Produktbildung.
Die für diesen Fall umgestaltete Michaelis-Menten-Gleichung enthält in
ihrem Nenner zwei Faktoren: Einer davon multipliziert die Michaelis-Konstante
der nicht-inhibierten Reaktion, der andere die Substratkonzentration. Wenn man
11
das Lineweaver-Burk-Diagramm einerseits ohne den Inhibitor, andererseits mit
zwei unterschiedlichen Inhibitor-Konzentrationen beim Konstanthalten der
Enzymkonzentration aufnimmt, bekommt man drei Geraden mit unterschiedlichen
Steigungen, die im Gegensatz zu der reversiblen und kompetitiven Inhibition
unterschiedliche Steigungen haben, und im Gegensatz zu der kompetitiven
Inhibition, sich nicht an der Ordinatenachse des Koordinatensystems schneiden.
Die Werte von α beziehungsweise α' können ebenso ausgerechnet werden, wie bei
der kompetitiven beziehungsweise unkompetitiven Inhibition.
(Abb. 9) Ein irreversibler Inhibitor bildet eine sehr stabile kovalente Bindung
mit einer der funktionellen Gruppen in dem aktiven Zentrum des Enzyms, oder
zerstört dort eine der essenziellen funktionellen Gruppen. Ein kovalent bindender
Inhibitor kann nützliche Information bezüglich des enzymatischen
Reaktionsmechanismus liefern. Mit seiner Hilfe können nämlich Aminosäurereste
mit Schlüsselposition in dem aktiven Zentrum des Enzyms dadurch ermittelt
werden, dass man nach Inhibition das Enzym hydrolysiert, und diejenige
Aminosäure identifiziert, mit der der Inhibitor kovalent verknüpft ist. Zum Beispiel
wurde die Schlüsselposition von Serin in Chymotrypsin mittels Diisopropylfluorophosphat ermittelt, das eine kovalente Bindung nur mit Serin herstellen kann.
Eine besondere Klasse der irreversiblen Inhibition ist die so genannte
Selbstmord-Inhibition. Ein Selbsmord-Inhibitor ist ein modifiziertes Substrat das
zuerst reversibel und kompetitiv in dem aktiven Zentrum des Enzyms gebunden
wird. Der entstehende Enzym-Inhibitor-Komplex wird danach durch den normalen
enzymatischen Mechanismus in das normale Produkt und eine sehr reaktionsfähige
Verbindung überführt, die sich irreversibel an eine essentielle funktionelle Gruppe
in dem aktiven Zentrum des Enzyms bindet, oder sie zerstört. Die Wirkungsweise
einiger neuer Arzneimittel beruht auf der Selbstmord-Inhibition. Solche
Arzneimittel wurden in der Kenntnis der betreffenden Reaktionsmechanismen
12
erarbeitet. Ein gutes Selbstmord-Inhibitor-Arzneimittel ist nur für ein einziges
Enzym spezifisch, und verursacht wenige Nebenwirkungen.
(Abb. 10) Was die Abhängigkeit der Enzymaktivität von dem pH-Wert
betrifft, besitzt jedes Enzym einen optimalen pH-Wert. Ist der pH-Wert seiner
Umgebung höher oder niedriger, nimmt seine Aktivität ab. Das pH-Optimum von
den meisten Enzymen liegt in dem beinahe neutralen pH-Bereich, wie das der
Glucose-6-Phosphatase. Einige Enzyme haben aber ihr pH-Optimum bei extremen
pH-Werten, wie das Verdauungsenzym Pepsin, bei etwa pH 1,5. Der Grund für die
pH-Abhängigkeit der Enzyme ist, dass Seitenketten einiger Aminosäureresten in
ihren aktiven Zentren schwache Säuren oder Basen mit unterschiedlichem pHOptimum sind. Diese Seitenketten dissoziieren bei unterschiedlichen pH-Werten in
unter-schiedlichen Massen. Dies beeinflusst die räumliche Anordnung der
funktionellen Gruppen in dem aktiven Zentrum des Enzyms, und dadurch seine
Aktivität.