grundlagen der algebra

G RUNDLAGEN DER A LGEBRA
Notizen zur Vorlesung im Sommersemester 2010
Universität Stuttgart, Studiengang Mathematik
Rohfassung
compiliert am 10. Januar 2011
Copyright  2010 Michael Eisermann
www.igt.uni-stuttgart.de/eiserm
Für die Mitteilung von Unklarheiten und Fehlern aller Art
sowie für Vorschläge und Kritik bin ich stets dankbar!
ii
Inhaltsverzeichnis
Kapitel 0.
Vorwort
i
Kapitel 1.
Konstruktion mit Zirkel und Lineal
1
§1A. Was können wir mit Zirkel und Lineal konstruieren? – §1B. Von der Geometrie zur
Algebra. – §1C. Algebraische Antworten auf geometrische Fragen. – §1D. Wie geht es
weiter? – §1E. Übungen und Ergänzungen.
I
Grundlagen der Ringtheorie
Kapitel 2.
Monoide und Gruppen
15
§2A. Einführung und Überblick. – §2B. Verknüpfungen. – §2C. Monoide. – §2D. Gruppen. – §2E. Kommutativität. – §2F. Der Satz von Cayley. – §2G. Quotientenstrukturen. –
§2H. Freie Monoide und freie Gruppen. – §2I. Übungen und Ergänzungen.
Kapitel 3.
Ringe und Körper
47
§3A. Ringe und Körper. – §3B. Homomorphismen. – §3C. Integritätsringe und Bruchkörper.
– §3D. Ideale und Quotientenringe. – §3E. Neue Ringe aus alten. – §3F. Der chinesische
Restsatz. – §3G. Monoidringe. – §3H. Übungen und Ergänzungen.
Kapitel 4.
Polynomringe
79
§4A. Definition und universelle Eigenschaft. – §4B. Gradfunktion und euklidische Division. – §4C. Faktorisierung von Nullstellen. – §4D. Übungen und Ergänzungen.
Kapitel 5.
Teilbarkeitstheorie in Integritätsringen
89
§5A. Motivation. – §5B. Grundbegriffe. – §5C. Euklidische Ringe. – §5D. Hauptidealringe. – §5E. Faktorielle Ringe. – §5F. Teilerfremdheit und Invertierbarkeit. – §5G. Primideale und maximale Ideale. – §5H. Übungen und Ergänzungen.
Kapitel 6.
Primfaktorzerlegung in Polynomringen
111
§6A. Motivation und Überblick. – §6B. Primfaktorzerlegung. – §6C. Exponentenbewertung und Normierung. – §6D. Inhalt und Normierung von Polynomen. – §6E. Der Satz
von Gauß. – §6F. Fortsetzung des ggT von einem Ring R auf den Polynomring R[X]. –
§6G. Irreduzibilitätskriterien. – §6H. Übungen und Ergänzungen.
Kapitel 7.
Matrizenringe und der Elementarteilersatz
§7A. Einführung und Motivation. – §7B. Matrizenringe. – §7C. Die Determinante. –
§7D. Der Algorithmus von Gauß–Bézout. – §7E. Eindeutigkeit der Elementarteiler.
iii
135
Kapitel 8.
Moduln und Vektorräume
153
§8A. Motivation und Überblick. – §8B. Moduln über einem Ring. – §8C. Quotientenmoduln und Isomorphiesätze. – §8D. Basen und freie Moduln. – §8E. Moduln über Hauptidealringen. – §8F. Vektorräume. – §8G. Beispiele, Anwendungen, Übungen.
II
Grundlagen der Gruppentheorie
Kapitel 9.
Grundbegriffe der Gruppentheorie
175
§9A. Der Satz von Lagrange. – §9B. Normale Untergruppen und Quotientengruppen. –
§9C. Kommutieren. – §9D. Zyklische Gruppen. – §9E. Konjugation und innere Automorphismen. – §9F. Operationen. – §9G. Übungen und Ergänzungen.
Kapitel 10.
Symmetrische und alternierende Gruppen
197
§10A. Die symmetrische Gruppe. – §10B. Zykelzerlegung. – §10C. Die Signatur. – §10D. Die
alternierende Gruppe. – §10E. Einfache Gruppen. – §10F. Semidirekte Produkte. – §10G. Übungen
und Ergänzungen.
Kapitel 11.
Sylow–Sätze und Anwendungen
221
§11A. Einführung und Überblick. – §11B. Die Sylow-Sätze. – §11C. Einfache Klassifikationssätze. – §11D. Auflösbare Gruppen. – §11E. Übungen und Ergänzungen.
III
Grundlagen der Körpertheorie
Kapitel 12.
Körpererweiterungen
233
§12A. Einleitung und Überblick. – §12B. Körpererweiterungen. – §12C. Algebraische Erweiterungen. – §12D. Zerfällungskörper. – §12E. Algebraischer Abschluss. – §12F. Übungen
und Ergänzungen.
Kapitel 13.
Endliche Körper
253
§13A. Einführung und Überblick. – §13B. Klassifikation endlicher Körper. – §13C. Konstruktion endlicher Körper. – §13D. Übungen und Ergänzungen.
Kapitel 14.
Der Hauptsatz der Galois-Theorie
265
§14A. Einleitung und Überblick. – §14B. Separable Erweiterungen. – §14C. Normale
Erweiterungen. – §14D. Galois-Gruppe einer Gleichung.
Kapitel 15.
Anwendungen der Galois-Theorie
§15A. Konstruierbarkeit mit Zirkel und Lineal. – §15B. Auflösbare Erweiterungen.
iv
283
KAPITEL 0
Vorwort
Was ist und was soll die Algebra?
Mathematik ist die Lehre von Zahlen und Figuren. Über die Jahrhunderte hat sich
eine Erfahrung herausgebildet und erhärtet: mathematische Methoden lassen sich erstaunlich erfolgreich auf eine Fülle von natürlichen Phänomenen und menschlichen Aktivitäten
anwenden. Eine typische Anwendungen sind Gleichungen, und die Algebra ist, grob gesagt,
die mathematische Theorie zum Lösen von Gleichungen. Sie untersucht dazu die Struktur
der Rechenoperationen und der zugehörigen Objekte.
Die Algebra ist die mathematische Theorie zum Lösen von Gleichungen. Wir werden uns dieses Semester vor allem mit polynomiellen Gleichungen beschäftigen:
a1 X + a0 = 0
2
a2 X + a1 X + a0 = 0
a3 X 3 + a2 X 2 + a1 X + a0 = 0
a4 X 4 + a3 X 3 + a2 X 2 + a1 X + a0 = 0
a5 X 5 + a4 X 4 + a3 X 3 + a2 X 2 + a1 X + a0 = 0
etc. . .
Das einfachste Beispiel sind Gleichungen der Form a · x + b = 0. Für a 6= 0 hat diese
Gleichung die Lösung x = −b/a. Die hierzu nötigen Operationen + und · und ihre Inversen
− und / führen unmittelbar zum algebraischen Begriff des Körpers. Lineare Gleichungssysteme über einem Körper werden in der linearen Algebra untersucht.
In dieser Vorlesung werden wir uns mit nicht-linearen, und zwar polynomiellen Gleichungen beschäftigen. Das einfachste und bekannteste Beispiel ist die quadratische Gleichung ax2 + bx + c = 0. Für a 6= 0 hat
√ diese Gleichung zwei Lösungen, und diese können
−b± b2 −4ac
durch die berühmte Formel x =
ausgedrückt werden. Diese Formel nutzt ne2a
ben den Körperoperationen nur das Ziehen von Quadratwurzeln. In diesem Sinne ist die
quadratische Gleichung also “durch Wurzeln auflösbar”.
Ähnliche Lösungen für Gleichungen dritten Grades wurden von den italienischen Mathematikern Nicolo Tartaglia (1499–1557) und Gerolamo Cardano (1501–1576) gefunden,
i
ii
Kapitel 0. Vorwort
und Gleichungen vierten Grades wurden von Cardanos Schüler Lodovico Ferrari (1522–
1565) gelöst. Diese Lösungsformeln sind zwar zunehmend kompliziert, benutzen aber nur
die Körperoperationen und das Wurzelziehen.
Nach solchen Lösungsformeln für Gleichungen fünften und höheren Grades wurde
mehrere Jahrhunderte lang vergeblich gesucht. Dann kam die große Überraschung: der norwegische Mathematiker Niels Henrik Abel (1802–1829) bewies, dass es derartige allgemeine Formeln nicht geben kann. Die tieferen Gründe hierfür wurden von dem französischen
Mathematiker Évariste Galois (1811–1832) aufgedeckt. Die Entwicklung der nach ihm benannten Galois-Theorie ist das Hauptziel dieser Vorlesung.
Die Grundidee ist einfach: zu jeder Gleichung betrachtet man die Symmetrien, die zwischen ihren Wurzeln bestehen. Dies führt zum Begriff der Gruppe: die Galois-Gruppe misst
die Kompliziertheit einer Gleichung, und eine auflösbare Gleichung erkennt man daran,
dass ihre Galois-Gruppe auflösbar ist.
Die Galois-Theorie ist ein faszinierendes Beispiel dafür, dass manchmal konkrete Probleme erst lösbar werden, wenn man sie mit der nötigen Abstraktion behandelt. So entsteht
aus der klassischen Algebra (über den reellen und komplexen Zahlen) durch Abstraktion und Vereinheitlichung die moderne Algebra (über allgemeineren Ringen und Körpern).
Die Vorlesung wird sich hierzu mit dem nötigen Handwerkszeug der Gruppen, Ringe und
Körper befassen, die auch überall sonst in der Algebra unerlässlich sind.
Algebra ist das Studium von Verknüpfungen. Viele konkrete Rechnungen weisen
Ähnlichkeiten und Gesetzmäßigkeiten auf. Diese können gewinnbringend im Rahmen allgemeinener Strukturen untersucht werden und tragen so wohlklingende Namen wie Ring
oder Körper. Diese Konzepte treten schon beim Aufbau des Zahlensystems natürlich auf:
(N, +, ·) ⊂ (Z, +, ·) ⊂ (Q, +, ·) ⊂ (R, +, ·) ⊂ (C, +, ·)
Solche Strukturen, insbesondere Ringe, findet man aber in vielen Situationen:
• Die Menge Q[X] der Polynome (zum Beispiel über dem Körper Q der rationalen Zahlen) mit ihrer Addition + : Q[X] × Q[X] → Q[X] und ihrer Multiplikation
· : Q[X] × Q[X] → Q[X] bildet einen kommutativen Ring.
• Die Menge M = Cn×n der n × n-Matrizen (zum Beispiel über dem Körper C der
komplexen Zahlen) mit ihrer Addition + : M × M → M und ihrer Multiplikation
· : M × M → M bildet einen nicht-kommutativen Ring.
Das Verständnis der allgemeinen Gesetzmäßigkeiten erweist sich als ungemein effizient
beim Lösen konkreter Probleme. Die Entwicklung der hierzu nötigen Theorie wird uns das
ganze Semester beschäftigen — und wird doch nur ein bescheidener Anfang sein können.
Algebra ist Koordinatisierung. Sie kennen hierzu aus dem ersten Studienjahr die lineare Algebra und analytische Geometrie. Die folgende Einführung präsentiert ein konkretes und historisch bedeutsames Beispiel: die Konstruktion mit Zirkel und Lineal.
Michael Eisermann hwww.igt.uni-stuttgart.de/eisermi
KAPITEL 1
Konstruktion mit Zirkel und Lineal
In diesem ersten Kapitel stürzen wir uns in ein klassisches Problem der ebenen Geometrie:
die Konstruktion mit Zirkel und Lineal. Diese Einführung ist ein hors d’œuvre; sie zeigt einerseits, dass man mit Schulmathematik und ein wenig Ausdauer schon recht weit vordringen kann. Andererseits zeigt sie auch die Notwendigkeit tiefergehender Begriffsbildungen.
Deren systematischer Aufbau ist das Ziel der Algebra.
§1A. Was können wir mit Zirkel und Lineal konstruieren?
Konstruktionen mit Zirkel und Lineal sind seit der Antike sowohl von praktischem
als auch von theoretischem Interesse, und bis heute in der mathematischen Schulbildung
präsent. Aus praktischer Sicht möchte man wissen, wie man gewisse Figuren konstruiert.
Aus theoretischer Sicht stellt sich die Frage, welche Konstruktionen überhaupt möglich
sind, oder umgekehrt, welche nicht und warum.
§1Aa. Grundkonstruktionen. Beginnen wir mit drei einfachen Fragen der ebenen
Geometrie, wie sie den meisten aus der Schule vertraut sein dürfte:
1. Zu gegebenen Längen a, b konstruiere man die Längen a + b und a − b.
2. Zu gegebenen Längen 1, a, b konstruiere man die Längen
√ a · b und a/b.
3. Zu gegebenen Längen 1, a konstruiere man die Länge a.
Hier und im Folgenden heiße konstruieren (ohne weiteren Zusatz) stets konstruieren
mit Zirkel und Lineal. Die Formulierung dieser Fragen verweist bereits auf die Verbindung
von Geometrie und Algebra, die sich als äußerst glücklich und fruchtbar erweisen wird.
Für jede ernsthafte Untersuchung ist es unerlässlich genau zu definieren, was wir unter
der Konstruktion mit Zirkel und Lineal verstehen. Hierzu sei M eine vorgegebene Menge
von Punkten in der Ebene. Wir bezeichnen mit G (M) die Menge aller Geraden, die durch
zwei verschiedenen Punkte von M laufen, und mit K (M) die Menge aller Kreise, deren
Mittelpunkt in M liegt und deren Radius der Abstand zweier verschiedener Punkte aus M
ist. Ein Punkt P heißt in einem Schritt aus M konstruierbar, wenn er Schnittpunkt ist von
• zwei verschiedenen Geraden aus G (M) oder
• zwei verschiedenen Kreisen aus K (M) oder
• einer Geraden aus G (M) und einem Kreis aus K (M).
1
2
Kapitel 1. Konstruktion mit Zirkel und Lineal
Ein Punkt P heißt in n Schritten aus M konstruierbar, wenn es eine Folge P1 , P2 , . . . , Pn =
P gibt, sodass jeder Punkt Pk in einem Schritt aus M ∪ {P1 , . . . , Pk−1 } konstruierbar ist.
Definition 1A1. Ein Punkt P heißt aus M konstruierbar, wenn es eine natürliche Zahl n ∈ N
gibt, sodass P in n Schritten aus M konstruierbar ist.
Diese Definition präzisiert, wie man mit Zirkel und Lineal neue Punkte aus alten konstruiert. Die möglichen Konstruktionen hängen davon ab, welche Punkte vorgegeben sind;
im einfachsten Fall nimmt man an, dass anfänglich nur zwei Punkte vorgegeben sind. Eine
Länge oder (positive) reelle Zahl ist der Abstand zweier Punkte. Eine bestimme Zahl zu
konstruieren bedeutet zwei Punkte zu konstruieren, die den gewünschten Abstand haben.
Übung 1A2. Man löse die ersten drei Fragen durch Angabe geeigneter Konstruktionen.
§1Ab. Vier klassische Probleme der Geometrie. Ausgehend von den obigen Grundkonstruktionen möchten wir die Frage der Konstruierbarkeit mit Zirkel und Lineal erkunden. Als Leitfaden dienen uns hierzu die folgenden vier Probleme:
1.
2.
3.
4.
Welche regelmäßigen n-Ecke lassen sich mit Zirkel und Lineal konstruieren?
Lässt sich √
zu jedem Winkel θ der Winkel θ /3 konstruieren? (Winkeldreiteilung)
Lässt sich 3 2 mit Zirkel und Lineal konstruieren? (Verdopplung des Würfels)
Lässt sich zu einem gegebenen Kreis ein flächengleiches Quadrat konstruieren?
(Dies ist die sprichwörtlich gewordene Quadratur des Kreises.)
Wir werden in diesem einführenden Teil zunächst einen vollkommen elementaren Zugang wählen, der allein mit Schulmathematik auskommt, und doch einen beachtlichen Teil
lösen können. Wie immer bedeutet elementar nicht unbedingt einfach. Nehmen wir also
unseren Mut zusammen und seien wir kreativ!
Mit den entsprechenden Werkzeugen der Algebra werden sich viele Fragen später wie
von selbst lösen. In Ermangelung dieser Werkzeuge werden wir es in diesem Kapitel mit
bloßen (wenn auch geschickten) Händen versuchen. Wer sich hierbei ein paar Schwielen
geholt hat, wird die spätere Bequemlichkeit umso mehr zu schätzen wissen.
§1B. Von der Geometrie zur Algebra
§1Ba. Vom Problem zum Modell: analytische Geometrie. Modellieren bedeutet, ein
Problem in eine geeignete Sprache zu übersetzen, in der sich das Wesentliche des Problems
beschreiben und – soweit möglich – lösen lässt. Für die Konstruierbarkeit mit Zirkel und
Lineal folgen wir einer einfachen aber radikalen Idee: der Koordinatisierung.
Kurz gesagt: wir identifizieren die Ebene mit dem Raum R2 .
Etwas ausführlicher: Gegeben seien zwei verschiedene Punkte O und P der Ebene. Durch diese beiden Punkte verläuft genau eine Gerade. Diese können wir durch den Körper R parametrisieren, wobei
0 7→ O und 1 7→ P, sodass die Körperoperationen a + b, a − b, ab, a/b und die Anordnung der Punkte
respektiert werden. (Hierzu wäre noch wesentlich mehr zu sagen, aber wir verzichten auf eine axiomatische Herleitung zugunsten eine raschen Skizze.) Anschließend konstruieren wir die Senkrechte
durch O und wählen hierauf einen Punkt Q mit Abstand |OQ| = |OP|. Auch die Gerade durch O und
Q parametrisieren wird durch R. Die orthogonale Projektion auf diese beiden Achsen ordnet jedem
Punkt X der Ebene ein Paar reeller Zahlen (x, y) ∈ R2 zu; diese werden die Koordinaten des Punktes
X genannt. (Zum Beispiel gelten die Entsprechungen O ↔ (0, 0), P ↔ (1, 0), Q ↔ (0, 1).) Umgekehrt
Michael Eisermann hwww.igt.uni-stuttgart.de/eisermi
§1B. Von der Geometrie zur Algebra
3
entsprechen je zwei Koordinaten (x, y) ∈ R2 genau einem Punkt der Ebene. (Gewöhnlich nennt man
dann die Gerade OP die x-Achse und die Gerade OQ die y-Achse.) Auf diese Weise können wir die
Ebene mit dem Raum R2 identifizieren.
Was haben wir so gewonnen? Mit Koordinaten können wir rechnen!
Satz 1B1. Sei M ⊂ R2 eine Menge von Punkten und sei K := Koord(M) ⊂ R die Menge
ihrer Koordinaten. Sei M̄ ⊂ R2 die Menge der aus M mit Zirkel und Lineal konstruierbaren
Punkte. Sei K̄ ⊂ R die Menge der aus K konstruierbaren
Zahlen durch Anwendung der fünf
√
Operationen a + b, a − b, ab, a/b für b 6= 0, und a für a > 0. Dann gilt Koord(M̄) = K̄.
B EWEIS . Die Inklusion K̄ ⊂ Koord(M̄) folgt aus Übung 1A2: Die reellen Zahlen in K
ergeben sich aus M durch Projektion auf die Koordinatenachsen, und die fünf genannten
Operationen sind konstruierbar mit Zirkel und Lineal. (Man führe dies explizit aus.)
Für die umgekehrte Inklusion Koord(M̄) ⊂ K̄ müssen wir zeigen, dass die Koordinaten
der mit Zirkel und Lineal aus M konstruierbaren Punkte sich durch Anwendung der fünf
Operationen berechnen lassen. Hierzu fassen wir die geometrischen Objekte algebraisch:
Die Gerade G durch zwei verschiedene Punkte (x0 , y0 ) und (x1 , y1 ) in M ist die Menge
G = {(x, y) ∈ R2 | (x − x0 )(y1 − y0 ) − (y − y0 )(x1 − x0 ) = 0}.
p
Der Kreis K um (x0 , y0 ) ∈ M mit Radius r = (x1 − x2 )2 + (y1 − y2 )2 , gegeben durch
den Abstand zweier verschiedener Punkte (x1 , y1 ) und (x2 , y2 ) in M, ist die Menge
K = {(x, y) ∈ R2 | (x − x0 )2 + (y − y0 )2 = r2 }.
Geraden G ∈ G (M) und Kreise K ∈ K (M) sind demnach Punktmengen der Form
G = {(x, y) ∈ R2 | ax + by + c = 0}
2
2
und
2
K = {(x, y) ∈ R | x + y + ax + by + c = 0}.
Hierbei ergeben sich die Koeffizienten a, b, c ∈ R aus den Koordinaten Koord(M) durch
die rationalen Operationen +, −, ·, /.
Betrachten wir schließlich die Schnittpunkte solcher Mengen. Der Schnitt von zwei
Geraden führt auf ein System von zwei linearen Gleichungen mit zwei Unbekannten; ihre
Lösung berechnet sich durch die rationalen Operationen aus den Koeffizienten. Der Schnitt
von zwei Kreisen, oder einem Kreis und einer Geraden, führt auf eine quadratische Gleichung; ihre Lösungen berechnen sich durch die rationalen Operationen und eine Quadratwurzel. Damit ist die geometrisch-algebraische Äquivalenz bewiesen.
Übung 1B2. Führen Sie die im Beweis genannten Rechnungen explizit aus.
§1Bb. Teilkörper der reellen Zahlen. Wir beginnen mit einer einfachen Beobachtung: Sei K die Menge aller Zahlen, die sich aus 1 durch wiederholte Anwendung der
rationalen Operationen +, −, ·, / konstruieren lassen. Dann ist K = Q genau die Menge
der rationalen Zahlen. Ausgehend von 1 erhält man nämlich N ⊂ K durch Addition, damit
Z ⊂ K und schließlich Q ⊂ K. Für die umgekehrte Inklusion Q ⊃ K genügt es festzustellen,
dass Q abgeschlossen ist unter rationalen Operationen.
Da die rationalen Operationen eine herausragende Rolle spielen, heben wir sie durch
die folgende Definition besonders hervor:
Rohfassung compiliert am 10. Januar 2011
4
Kapitel 1. Konstruktion mit Zirkel und Lineal
Definition 1B3. Eine Teilmenge K ⊂ R heißt Körper (genauer Teilkörper der reellen Zahlen) wenn sie die Zahl 1 enthält und mit je zwei Zahlen a, b ∈ K auch deren Summe a + b,
Differenz a − b, Produkt ab, und Quotient a/b. (Bei letzterem b 6= 0 wird vorausgesetzt.)
Wir werden später allgemein definieren, was ein Körper ist. Fürs Erste genügt uns jedoch diese Definition, da wir in diesem Kapitel mit Teilkörpern von R auskommen.
Beispiel 1B4. Die gesamte Menge R ist ein Körper. Weder die Teilmenge N der natürlichen
Zahlen noch die Teilmenge Z der ganzen Zahlen sind Körper. Die Teilmenge Q der rationalen Zahlen ist hingegen ein Körper. und zwar der kleinste Teilkörper von R: wir haben
gerade gesehen, dass jeder Teilkörper Q enthält.
Die folgende Konstruktion liefert unendlich viele weitere Beispiele:
Proposition 1B5. Sei K ⊂ R ein Körper und sei c ∈ K, c > 0. Dann ist die Menge
√
√
K[ c] := {a + b c | a, b ∈ K}
ein Teilkörper von R.
√
Genauer gesagt
√ ist K[ c] der kleinste Teilkörper von R der sowohl den Körper K als
auch das Element c enthält. Wir nennen dies eine quadratische Erweiterung von K.
√
√
√
B EWEIS . In√Falle c ∈ K gilt√trivialerweise
K[ c] = K. Nehmen wir also c ∈
/ K an.
√
Seien x = a + b c und y = a0 + b0 c in K[ c]. Dann finden wir
√
• x + y = (a + a0 ) + (b + b0 )√c ,
• x − y = (a − a0 ) + (b − b0 ) c , √
• x · y = (aa0√+ bb0 c) +√(ab0 + a0√
b) c ,
0 −bb0 c
0
0 √
a+b √c a0 −b0 √c
a+b √c
+ aa02b−ab
• x/y = a0 +b0 c = a0 +b0 c · a0 −b0 c = aa
c.
a02 −b02 c
−b02 c
Da K ein Körper ist, sind alle so aus a, b, a0 , b0 , c ∈
√K berechneten Koeffizienten wieder in
K, und x + y, x − y, xy, x/y liegen demnach in K[ c]. Notwendige Präzisierung: Wann ist
02 c gleich Null? Aus a02 − b02 c = 0 und b0 6= 0 folgt c = a02 /b02 , entgegen
der Nenner a02 − b√
unserer Annahme c ∈
/ K. Daher kann a02 − b02 c = 0 nur für a0 = b0 = 0 also y = 0 gelten.
Für alle y 6= 0 liegt x/y in K.
Definition 1B6. Eine Familie K0 ⊂ K1 ⊂ K2 ⊂ . . . von Körpern nennen wir einen Turm
√
quadratischer Erweiterungen wenn jeweils Kk+1 = Kk [ ck ] für ein ck ∈ Kk gilt.
Damit haben wir das passende Vokabular geschaffen, um die geometrisch-algebraische
Äquivalenz aus Satz 1B1 bequem formulieren zu können:
Satz 1B7. Für jede reelle Zahl x ∈ R sind folgende Aussagen äquivalent:
• x lässt sich mit Zirkel und Lineal aus dem Teilkörper K0 ⊂ R konstruieren.
• x liegt in einem Turm K0 ⊂ K1 ⊂ · · · ⊂ Kn quadratischer Erweiterungen in R.
Die Neuerung liegt hier in der sprachlichen und konzeptuellen Eleganz. Inhaltlich tiefliegender ist folgendes Beispiel, das wir hier nur zitieren aber nicht beweisen wollen:
Michael Eisermann hwww.igt.uni-stuttgart.de/eisermi
§1C. Algebraische Antworten auf geometrische Fragen
Beispiel 1B8 (unglaublich aber wahr). Durch eine raffinierte Rechnung fand Carl Friedrich
Gauß (seinem Tagebuch zufolge am 29. März 1796) folgende Gleichung:
2π
cos
17
r
q
q
q
√
√
√
√
1 √
1
=
17 − 1 + 34 − 2 17 +
17 + 3 17 − 34 − 2 17 − 2 34 + 2 17.
16
8
Aus dieser Formel folgt mithilfe des Satzes, dass das regelmäßige 17-Eck mit Zirkel und
Lineal konstruierbar ist. Dies war seit der griechischen Antike die erste große Neuerung
zu den klassischen Fragen der Konstruierbarkeit mit Zirkel und Lineal. Seine Entdeckung
bewegte den 18-jährigen Gauß sich endgültig der Mathematik zuzuwenden. Für eine schöne
und nicht minder raffinierte geometrische Konstruktion verweise ich auf Stewart §19.5.
Der vorhergehende Satz liefert ein praktisches Kriterium für die Konstruierbarkeit mit
Zirkel und Lineal, in Form einer notwendigen und hinreichenden algebraischen Begingung.
Die Menge M̄ ⊂ R2 aller aus M ⊂ R konstruierbaren Punkte lässt sich wie folgt charakterisieren durch den von M erzeugten quadratisch abgeschlossenen Teilkörper:
Satz 1B9. Sei M ⊂ R eine Menge mit 0, 1 ∈ M. Sei M̄ ⊂ R2 die Menge aller Punkte, die
sich hieraus mit Zirkel und Lineal konstruieren
lassen. Sei K ⊂ R der kleinste Teilkörper,
√
der M umfasst und zu jedem c > 0 auch c enthält. Dann gilt M̄ = K × K.
§1C. Algebraische Antworten auf geometrische Fragen
§1Ca. Das regelmäßige Fünfeck. Die Konstruktion des regelmäßigen n-Ecks gelingt
vergleichsweise leicht für n = 3, 4, 6, 8. Die Fälle n = 5 sowie n = 7, 9 sind kniffeliger, und
zwar aus entgegengesetzten Gründen: Um zu zeigen, dass eine Konstruktion möglich ist,
muss man eine Konstruktion finden. Um zu beweisen, dass eine Konstruktion unmöglich
ist, genügt es nicht geduldig zu scheitern. Man muss das Hindernis identifizieren!
Satz 1C1. Die folgenden regelmäßigen n-Ecke sind mit Zirkel und Lineal konstruierbar:
•
•
•
•
•
das gleichseitige Dreieck (n = 3).
das Quadrat (n = 4).
das regelmäßige Fünfeck (n = 5).
das regelmäßige Sechseck (n = 6).
das regelmäßige Achteck (n = 8).
B EWEIS . Nur der Fall n = 5 ist delikat. (Nach einigen Fehlversuchen könnte man den
Verdacht hegen, diese Konstruktion sei unmöglich. . . ) Um die Situation zu klären, nutzen
wir unsere oben entwickelten algebraischen Techniken!
Wir betrachten den Winkel θ = 2π/5 und das regelmäßige Fünfeck mit Zentrum 0 und
den Ecken (cos(kθ ), sin(kθ )) wobei k = 0, ±1, ±2. Regelmäßig bedeutet hierbei invariant
unter Drehung um θ . Der Schwerpunkt der fünf Ecken ist demnach 0. Wir finden somit
0 = 1 + 2 cos(θ ) + 2 cos(2θ )
= 1 + 2 cos θ + 2(2 cos2 θ − 1)
= 4 cos2 θ + 2 cos θ − 1
= x2 + x − 1
wobei x = 2 cos θ .
Rohfassung compiliert am 10. Januar 2011
5
6
Kapitel 1. Konstruktion mit Zirkel und Lineal
√
√
Dies erlaubt uns, den Wert x = 5−1
und damit cos(2π/5) = 5−1
zu berechnen. Nach Satz
2
4
1B1 kann man also das regelmäßige Fünfeck mit Zirkel und Lineal konstruieren.
Übung 1C2. Führen Sie eine Konstruktion des regelmäßigen 3, 4, 5, 6, 8-Ecks explizit aus.
Bemerkung 1C3. Das Argument des Schwerpunkts erlaubt uns nicht nur die genannte algebraische Relation zu beweisen sondern überhaupt erst zu finden. Die geometrische Interpretation ist daher eine nützliche Hilfe, sich die Rechnung zu merken und wiederzufinden,
falls Sie einmal auf einer einsamen Insel mathematische Zerstreuung suchen.
Bemerkung 1C4. Mithilfe der komplexen Zahlen kann man die algebraische Relation für
cos(2π/5) ebenso gut aus der geometrischen Summe 1 + eiθ + e2iθ + e3iθ + e4iθ = 0 und der
Eulerschen Formel cos θ = 21 (eiθ + e−iθ ) ableiten. Da ich eingangs die Schulmathematik
beschwor, ziehe ich in diesem Kapitel eine Formulierung ohne komplexe Zahlen vor.
Bemerkung 1C5. Wenn man das regelmäßige n-Eck mit Zirkel und Lineal konstruieren
kann, dann auch das regelmäßige 2n-Eck durch Halbierung des zentralen Winkels. Demnach sind auch regelmäßige Vielecke konstruierbar mit 3 · 2k Ecken, mit 4 · 2k Ecken, und
mit 5 · 2k Ecken, für alle k ∈ N.
Bemerkung 1C6. Wenn man das regelmäßige p-Eck und das regelmäßige q-Eck mit Zirkel
und Lineal konstruieren kann, wobei ggT(p, q) = 1, dann auch das regelmäßige pq-Eck. Es
2π
2π
gibt dann nämlich ganz Zahlen u, v ∈ Z sodass up + vq = 1. Daraus folgt 2π
pq = u q + v p .
Zum Beispiel kann man somit das regelmäßige 15-Eck konstruieren: es gilt 2 · 3 − 1 · 5 = 1,
2π
2π
und somit 2 · 2π
5 − 1 · 3 = 15 .
§1Cb. Das regelmäßige Siebeneck. Da unser algebraischer Ansatz so wunderbar für
das Fünfeck funktioniert, wollen wir das regelmäßige Siebeneck ebenso untersuchen.
Lemma 1C7. Die Zahl η = 2 cos(2π/7) erfüllt die Gleichung η 3 + η 2 − 2η − 1 = 0.
B EWEIS . Wir betrachten den Winkel θ = 2π/7 und das regelmäßige Siebeneck mit
Mittelpunkt 0 und den Eckpunkten (cos(kθ ), sin(kθ )) für k = 0, ±1, ±2, ±3. Diese sind
invariant unter Drehung um θ , ihr Schwerpunkt ist demnach 0. So finden wir
0 = 1 + 2 cos(θ ) + 2 cos(2θ ) + 2 cos(3θ )
= 1 + 2 cos θ + (4 cos2 θ − 2) + (8 cos3 θ − 6 cos θ )
= 8 cos3 θ + 4 cos2 θ − 4 cos θ − 1
= η 3 + η 2 − 2η − 1.
Hierbei benutzen wir cos(3θ ) = 4 cos3 θ − 3 cos θ sowie cos(2θ ) = 2 cos2 θ − 1.
Bemerkung 1C8. Die algebraische Relation η 3 + η 2 − 2η − 1 = 0 bietet uns einen konkreten Zugriff auf die Zahl η = 2 cos(2π/7). Wenn man komplexe Zahlen verwenden möchte,
kann man diese Relation ebenso aus der geometrischen Summe 1+eiη +e2iη +e3iη +e4iη +
e5iη + e6iη = 0 und der Eulerschen Formel cos η = 12 (eiη + e−iη ) ableiten.
Lemma 1C9. Das Polynom X 3 + X 2 − 2X − 1 hat keine rationale Nullstellen.
Michael Eisermann hwww.igt.uni-stuttgart.de/eisermi
§1C. Algebraische Antworten auf geometrische Fragen
7
B EWEIS . Angenommen, es gäbe eine rationale Zahl x = ab so dass x3 + x2 − 2x − 1 = 0.
Hierbei ist a, b ∈ Z und b ≥ 1, und wir können ggT(a, b) = 1 annehmen. Wir erhalten so
a3 +a2 b−2ab2 −b3 = 0. Daraus sehen wir: a teilt b, also a = ±1, und b teilt a, also b = 1. Es
bleibt demnach nur die Möglichkeit x = ±1. Aber x = ±1 erfüllt nicht x3 + x2 − 2x − 1 = 0.
Also erfüllt keine rationale Zahl x die Gleichung x3 + x2 − 2x − 1 = 0.
Insbesondere ist η = 2 cos(2π/7) nicht rational. Um cos(2π/7) mit Zirkel und Lineal
zu konstruieren brauchen wir also mindestens eine Quadratwurzel. Reicht eine?
√
Lemma 1C10. Sei K0 ⊂ K1 = K0 [ c] eine quadratische Erweiterung. Wenn das Polynom
X 3 + X 2 − 2X − 1 eine Wurzel in K1 hat, dann liegt auch bereits in K0 eine solche Wurzel.
√
B EWEIS . Wir haben x3 + x2 − 2x − 1 = 0 für ein Element x ∈ K1 , das heißt x = a + b c
mit a, b, c ∈ K0 , c > 0. Wir entwickeln
√
0 = x3 + x2 − 2x − 1 = α + β c
und nach einer kleinen Rechnung finden wir
α = a3 + 3ab2 c + a2 + b2 c − 2a − 1,
β = 3a2 b + b3 c + 2ab − 2b.
Wir unterscheiden zwei Fälle:
√
• Wenn β 6= 0, dann folgt sofort c = −α/β ∈ K0 , also auch x ∈ K0 .
2
und α = −8a3 − 8a2 + 2a + 1.
• Wenn β = 0, dann c = 2−2a−3a
b2
1
Wegen α = 0 folgt a 6= 0, und y = 2a
∈ K0 erfüllt y3 + y2 − 2y − 1 = 0.
In beiden Fällen hat X 3 + X 2 − 2X − 1 eine Wurzel in K0 .
Dieses Argument können wir nun iterieren und erhalten daraus folgendes Ergebnis:
Satz 1C11. Das regelmäßige Siebeneck ist nicht mit Zirkel und Lineal konstruierbar.
B EWEIS . Die Konstruktion des regelmäßigen Siebenecks ist äquivalent zur Konstruktion der Zahl cos(2π/7). Nehmen wir an, η = 2 cos(2π/7) sei mit Zirkel und Lineal konstruierbar ausgehend von der Länge 1. Dann gäbe es einen Turm Q = K0 ⊂ K1 ⊂ · · · ⊂
Kn−1 ⊂ Kn ⊂ R quadratischer Erweiterungen in R sodass η ∈ Kn . Also hat das Polynom
X 3 + X 2 − 2X − 1 eine Wurzel in Kn . Das vorhergehende Lemma zeigt, dass eine Wurzel in
Kn−1 liegt, demnach auch in Kn−2 , . . . , und schließlich in K0 = Q. Aber X 3 +X 2 −2X −1 hat
keine rationale Wurzel. Also ist η = 2 cos(2π/7) nicht mit Zirkel und Lineal konstruierbar,
und damit auch nicht das regelmäßige Siebeneck.
§1Cc. Das regelmäßige Neuneck. Ein mathematisches Argument, das einmal funktioniert, ist ein Trick. Ein Argument, das zwei- oder mehrmals funktioniert ist eine Theorie.
Führen wir also unsere kleine Theorie noch ein klein wenig weiter, um die Konstruierbarkeit des regelmäßigen Neunecks zu klären. Diese zusätzliche Anstrengung lässt uns auch
eine unerwartete Antwort zur Dreiteilung des Winkels in den Schoß fallen.
Lemma 1C12. Die Zahl κ = 2 cos(2π/9) erfüllt die Gleichung κ 3 − 3κ + 1 = 0.
Rohfassung compiliert am 10. Januar 2011
8
Kapitel 1. Konstruktion mit Zirkel und Lineal
B EWEIS . Einerseits gilt cos(3θ ) = cos(2π/3) = −1/2. Andererseits wissen wir cos(3θ ) =
4 cos3 θ − 3 cos θ . Daraus folgt 8 cos3 θ − 6 cos θ + 1 = 0, also κ 3 − 3κ + 1 = 0.
Lemma 1C13. Das Polynom X 3 − 3X + 1 hat keine rationale Nullstellen.
B EWEIS . Angenommen, es gäbe eine rationale Zahl x = ab so dass x3 + x2 − 2x − 1 = 0.
Hierbei ist a, b ∈ Z und b ≥ 1, und wir können ggT(a, b) = 1 annehmen. Wir erhalten so
a3 +3ab2 −b3 = 0. Daraus sehen wir: a teilt b, also a = ±1, und b teilt a, also b = 1. Es bleibt
also nur die Möglichkeit x = ±1. Aber x = ±1 erfüllt nicht die Gleichung x3 − 3x + 1 = 0.
Also erfüllt keine rationale Zahl x die Gleichung x3 − 3x + 1 = 0.
Insbesondere ist κ = 2 cos(2π/9) nicht rational. Um cos(2π/9) mit Zirkel und Lineal
zu konstruieren brauchen wir also mindestens eine Quadratwurzel. Reicht eine?
Lemma 1C14. Sei K0 ⊂ K1 eine quadratische Erweiterung. Wenn das Polynom X 3 −3X +1
eine Wurzel in K1 hat, dann liegt auch bereits in K0 eine solche Wurzel.
√
B EWEIS . Wir haben x3 − 3x + 1 = 0 für ein Element x ∈ K1 , das heißt x = a + b c mit
a, b, c ∈ K0 , c > 0. Wir entwickeln
√
0 = x3 − 3x + 1 = α + β c
und nach einer kleinen Rechnung finden wir
α = a3 + 3ab2 c − 3a + 1,
β = 3a2 b + b3 c − 3b.
Wir unterscheiden zwei Fälle:
√
• Wenn β 6= 0, dann folgt sofort c = −α/β ∈ K0 , also auch x ∈ K0 .
2
• Wenn β = 0, dann c = 3−3a
und α = −8a3 + 6a + 1.
b2
Wegen α = 0 erfüllt y = −2a ∈ K0 die Gleichung y3 − 3y + 1 = 0.
In beiden Fällen hat X 3 − 3X + 1 eine Wurzel in K0 .
Als Krönung unserer Bemühungen erhalten wir das folgende Ergebnis:
Satz 1C15. Das regelmäßige Neuneck ist nicht mit Zirkel und Lineal konstruierbar.
Der Beweis verläuft genauso wie für das regelmäßige Siebeneck (1C11).
§1Cd. Die Dreiteilung des Winkels. Ausgehend von manchen Winkeln θ kann man
den Winkel θ /3 konstruieren. Dies gelingt zum Beispiel sehr leicht für einen rechten Winkel
θ = π/2. (Übung!) Zweitausend Jahre lang suchte man vergeblich nach einer Konstruktion
mit Zirkel und Lineal, die die Dreiteilung eines beliebigen Winkels ermöglicht.
Mit unseren algebraischen Hilfsmitteln können wir nun mühelos zeigen, dass eine solche Konstruktion im Allgemeinen unmöglich ist:
Satz 1C16. Es gibt keine Konstruktion mit Zirkel und Lineal, die einen beliebig vorgegebenen Winkel dreiteilt. Dies folgt aus einem einfachen und konkreten Gegenbeispiel: die
Dreiteilung des Winkels π/3 (d.h. 60◦ ) ist mit Zirkel und Lineal nicht möglich.
Michael Eisermann hwww.igt.uni-stuttgart.de/eisermi
§1D. Wie geht es weiter?
9
B EWEIS . Wir können das regelmäßige Sechseck mit Zirkel und Lineal konstruieren
(1C1). Wenn wir den zentralen Winkel π/3 dreiteilen könnten, dann entstünde so der Winkel π/9. Daraus ließe sich ein regelmäßiges Neuneck konstruieren. Dessen Konstruktion ist
aber mit Zirkel und Lineal nicht möglich (1C15).
Falls dieses Ergebnis Sie überrascht oder beunruhigt (was durchaus möglich und legitim
ist), dann sollten Sie die Gelegenheit nutzen, alle Argumente dieses Kapitels genau nachzuprüfen. Vielleicht hat sich ein Fehler eingeschlichen? Nach eingehender Prüfung werden
Sie Gewissheit haben und die nötigen Techniken sicher beherrschen.
§1D. Wie geht es weiter?
§1Da. Rückblick. Welche Kernideen haben zum Erfolg unserer mutigen Ersterkundung beigetragen? Rückblickend hat uns vor allem die Koordinatisierung große Dienste
erwiesen. Man beachte jedoch, dass weder die ursprüngliche Frage noch unsere Antwort
von Koordinaten sprechen: Das regelmäßige 3, 4, 5, 6, 8, 10-Eck ist mit Zirkel und Lineal
konstruierbar, das 7, 9-Eck hingegen nicht. Die Koordinatisierung ist gänzlich Teil der Modellierung, ein Konstrukt mit dessen Hilfe wir das ursprüngliche Problem umformuliert und
einer algebraischen Lösung zugänglich gemacht haben.
Unsere Ergebnisse, so bescheiden sie auch sein mögen, zeigen bereits eindrucksvoll,
wie fruchtbar die Verbindung von Geometrie und Algebra sein kann. Hierzu haben wir
folgende Techniken aus der Schulmathematik mobilisiert:
•
•
•
•
•
•
•
die Konstruktion mit Zirkel und Lineal,
die Benutzung von kartesischen Koordinaten,
Die Lösung von Gleichungen ersten und zweiten Grades,
algebraisches Rechnen
√ mit Quadratwurzeln in R,
die Irrationalität von 2 und einige Varianten,
die Parametrisierung des Kreises durch (cos θ , sin θ ),
die Gleichungen cos(2θ ) = 2 cos2 θ − 1 und cos(3θ ) = 4 cos3 θ − 3 cos θ .
Erstaunlicherweise ist nicht mehr als dies nötig gewesen.
Man kann sich naiv fragen, warum uns dieses Vorgehen heutzutage leicht fällt, nicht aber den Geometern des antiken Griechenlands. Entscheidend ist hierbei die Idee der Koordinatisierung, die den antiken Geometern weitgehend fremd und vor allem aber suspekt war. Erst durch die Koordinatisierung
jedoch wird Möglichkeit erschlossen, geometrische Phänomene mit Hilfe der Algebra zu beschreiben
und umgekehrt. Ohne dies hier vertiefen zu wollen, möchte ich damit eins unterstreichen: Wir erben
die Erfahrungen und Errungenschaften von über zweitausend Jahren wissenschaftlicher Entwicklung,
insbesondere auch mathematischen Fortschritts. Dieses Wissen wurde uns durch eine solide allgemeine Schulbildung weitergegeben und ermöglicht uns nun den Ausbau zu neuen Anwendungen. Zum
Beispiel haben wir gelernt, in Koordinaten zu denken und algebraische Rechnungen vorzunehmen.
Die Ergebnisse dieses Kapitels sind nur ein kleines Beispiel für die Früchte dieser Kenntnisse.
§1Db. Welche der klassischen Fragen bleiben noch offen? Wir haben nicht alle eingangs gestellten Fragen aus §1Ab auf einen Streich lösen können. Zur Konstruierbarkeit des
regelmäßigen n-Ecks kennen die Antwort für n ≤ 10. Die allgemeine Lösung wird sich aus
der Untersuchung des Kreisteilungspolynoms X n − 1 ergeben.
Rohfassung compiliert am 10. Januar 2011
10
Kapitel 1. Konstruktion mit Zirkel und Lineal
√
Die Verdopplung des Würfels, also die Konstruktion von 3 2 mit Zirkel und Lineal,
wird als Übung empfohlen und sollte mit den Techniken dieses Kapitels leicht fallen. (Zur
Geschichte dieses Delischen Problems lese man den englischen Wikipedia-Artikel. Wer
mutig und versiert ist, möchte vielleicht einen ordentlichen deutschen Wikipedia-Artikel
hierzu schreiben und pflegen.)
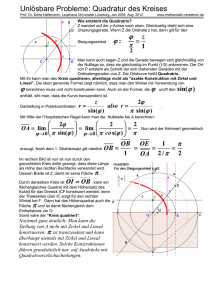
Zur Quadratur des Kreises haben wir bislang noch gar nichts sagen können: Lässt sich
zu einem gegebenen Kreis ein flächengleiches Quadrat konstruieren? Die Antwort folgt aus
der Untersuchung der Kreiszahl π: Der berühmte Satz von Hermite–Lindeman besagt, dass
π nicht algebraisch über Q ist, also nicht Nullstelle eines Polynoms X n + c1 X n−1 + · · · + cn
mit rationalen Koeffizienten c1 , . . . , cn ∈ Q sein kann. Wenn man dieses (deutlich tieferliegende) Ergebnis voraussetzt, so folgt die Antwort mit den Techniken dieses Kapitels: Allein
mit Zirkel und Lineal ist die Quadratur des Kreises nicht möglich.
§1Dc. Ausblick. Die Beweise der Sätze 1C11 und 1C15 sind etwas repetitiv: Diese
Rechnungen kommen zwar glücklich zum Ziel, sind auf Dauer aber lästig. Das ist der Preis,
den man für einen elementaren Zugang bezahlen muss. Unser Ziel wird sein, unseren mathematischen Werkzeugkasten durch allgemeinere Techniken zu erweitern. Es wird sich
herausstellen, dass mit ein wenig Abstraktion vieles leichter geht!
Nach Abschluss dieses einführenden und motivierenden Kapitels werden wir daher mit
der systematischen Entwicklung der Algebra beginnen. Das bisher Gesehene enthält hierzu
bereits den Keim einiger zentralen Ideen, die wir im Folgenden vertiefen werden:
• Der Begriff des Polynoms, seiner Wurzeln, und allgemein seiner Zerlegungen.
• Der Begriff der Symmetrie, und allgemein von Gruppen und ihren Operationen.
• Der Begriff des Körpers, der Körpererweiterung, und schließlich der Galois-Theorie.
§1E. Übungen und Ergänzungen
§1Ea. Von reellen zu komplexen Zahlen. Dieses Kapitel hat aus didaktischen Gründen
die Verwendung von komplexen Zahlen vermieden, vielleicht zu Unrecht. Mathematisch ist
die Frage durchaus interessant:
Übung 1E1. Sei M ⊂ R eine Menge mit 0, 1 ∈ M. Sei M̄ ⊂ R2 die Menge aller Punkte, die
sich hieraus mit Zirkel und Lineal konstruieren lassen. Ist M̄, als Teilmenge von C = R2
betrachtet, ein Teilkörper? Wie lässt sich die Menge M̄ ⊂ C algebraisch charakterisieren?
§1Eb. Variationen des Themas. Der Satz von Mohr–Mascheroni (1672/1797) besagt,
dass jeder Punkt, der mit Zirkel und Lineal konstruierbar ist, auch alleine mit Zirkel konstruierbar ist. Versuchen Sie doch mal, einige einfache Konstruktionen ohne Lineal durchzuführen! Wie könnte man den Satz von Mohr–Mascheron beweisen?
Wenn man hingegen nur das Lineal zulässt, dann sind manche Konstruktionen nicht
mehr möglich. (Warum?) Der Satz von Steiner besagt, dass ein Lineal genügt, wenn man
einen einzigen Kreis und seinen Mittelpunkt vorgibt. Daraus folgt, dass man alle Konstruktionen mit Zirkel und Lineal auch noch mit einem Lineal und einem rostigen Zirkel (mit
festem Radius) ausführen kann.
Michael Eisermann hwww.igt.uni-stuttgart.de/eisermi
§1E. Übungen und Ergänzungen
11
Zirkel und Lineal sind die klassische Wahl seit der Antike. Aber auch andere Werkzeuge
sind denkbar und führen eventuell zu anderen Konstruktionen. Zur weiteren Lektüre empfehle ich den Klassiker von Courant–Robbins: What is Mathematics?, Oxford University
Press 1996, sowie George E. Martin: Geometric Constructions, Springer 1997.
Rohfassung compiliert am 10. Januar 2011
TEIL I
Grundlagen der Ringtheorie
13