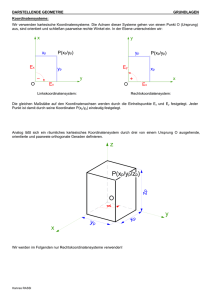
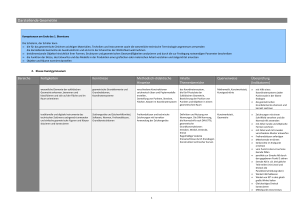
Aufgabenstellung zur¨Ubung 1

Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
2.5 Übung
Seite
1
Aufgabenstellung zur Übung 1
Hausübung zum Thema Orthogonale Axonometrie
Manfred Amrehn
Überblick:
Um die Wirkung eines Hochhauses darzustellen, soll eine
Orthogonale Axonometrie angefertigt werden.
Hinweise zur Bearbeitung:
Sie können sich zwischen drei verschiedenen Bearbeitungsweisen dieser Übung entscheiden:
– Lösungsweg 1: Kopierverfahren
Seite 2 + 3
– Lösungsweg 2: Einschneideverfahren
Seite 4 - 7
– Lösungsweg 2: Rechnereinsatz
Seite 8 - 10
Gruppenarbeit:
Je zwei Übungsteilnehmer arbeiten zusammen: Jeder
zeichnet eine orthogonale Axonometrie vom gemeinsamen Entwurf. Dabei müssen sich die Blickwinkel
gegen die Grundrissebene unterscheiden; wenn der Blick
,,von unten” gewählt wird, kann von beiden derselbe gestauchte Grundriss verwendet werden.
Entwurf Stadtbibliothek Saarbrücken
Abgabe
siehe Terminplan
Die abgegebenen Übungen werden von uns nur
korrigiert, wenn die Karteikarte ,,vollständig” beiliegt.
Hinweise zum Entwurf:
Der eigene Entwurf der groben Baumassen soll aus
folgenden Elementen bestehen:
– drei Quadern,
– einem Prisma und
– einem geraden Kreiszylinder .
Wählen Sie Höhe und Radius des Zylinders nicht zu klein, da
die entsprechenden Konstruktionen sonst leicht unübersichtlich
werden. Halten Sie den Entwurf einfach, da er später auch für
die Perspektive auf eine geneigte Bildebene verwendet wird.
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
2.5 Übung
Seite
2
Lösungsweg 1 : Kopierverfahren
Transparent 1 – Hinweise
1.
Grundriss und Aufriss
1.1. Zeichnen Sie das Hochhaus auf ein Transparent DIN
A3: auf das untere Drittel den Grundriss und auf
die oberen beiden Drittel den Aufriss. Ziehen Sie
die sichtbaren Gebäudekanten nach.
1.2. Legen Sie im Grundriss die Blickrichtung e 0 fest.
Um die Übung 4 nicht zu aufwendig zu gestalten,
sollte für
e0
ein Winkel zwischen 40˚und 50˚zu den
Hauptgebäuderichtungen gewählt werden.
Transparent 2 – Hinweise
2.
Laserkopie des Grundrisses
2.1. Der Grundriss ist mit Hilfe des Kopierverfahrens
2.5 Seite 6+7 zum axonometrischen Grundriss umzuwandeln: Als Blickrichtung wird e 0
übernommen; der Neigungswinkel der parallelen
Projektionsstrahlen gegen die Grundrissebene soll
20˚betragen.
2.2. Mit Hilfe der x, y−Zoom-Funktion eines Laserkopierers oder eines Bildbearbeitungsprogramms
(z.B. Photoshop) ist der Grundriss in Richtung von
x 0 =e 0 auf 36% zu stauchen und senkrecht dazu auf
106% zu dehnen.
Transparent 3 – Hinweise
3.
Axonometrie mit dem Kopierverfahren
3.1. Spannen Sie ein Transparent DIN A3 so über
den axonometrischen Grundriss (Laserkopie), dass
der untere Blattrand senkrecht zur gestauchten
Blickrichtung e 0 ist.
3.2. Konstruieren Sie die orthogonale Axonometrie des
Hochhauses.
3.3. Ziehen Sie die sichtbaren Kanten des Gebäudes
nach.
Darstellende Geometrie für Architekten III
2.5 Orthogonale Axonometrie
Transparent 1
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Übung
Transparent 2 – Lösungsweg 1 : Kopierverfahren
Transparent 3 – Lösungsweg 1 : Kopierverfahren
Seite
3
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
2.5 Übung
Seite
4
Lösungsweg 2 : Einschneideverfahren
Transparent 1
Transparent 2 – Hinweise
2.
Wahl der Blickrichtung
2.0. Spannen Sie das erste Transparent so verdreht auf,
dass e 0 senkrecht ist.
• So können Sie eine Reißschiene, Seilschiene oder
Zeichenmaschine zur Konstruktion verwenden.
• Zeichnen Sie die Koordinatenachsen ein.
2.1. Spannen Sie ein zweites Transparent DIN A2
(Hoch- oder Querformat) parallel zur Hilfslinie über
das erste Transparent.
2.2. Legen Sie senkrecht zu e 0 im Grundriss die
Schnittgerade einer Bildebene mit der Grundrissebene fest.
2.3. Legen Sie hierzu parallel für die Axonometrie die
Schnittgerade der Bildebene mit der Grundrissebene fest.
2.4. Wählen Sie an geeigneter Stelle den Neigungswinkel
der Projektionsstrahlen.
2.5. Ermitteln Sie das Spurpunktdreieck der orthogonalen Axonometrie.
2.6. Ermitteln Sie die Umklappung der Aufrissebene in
die Bildebene.
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
Transparent 2 – Lösungsweg 2 : Einscheideverfahren
2.5 Übung
Seite
5
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
2.5 Übung
Seite
6
Lösungsweg 2 : Einschneideverfahren
Transparent 3 – Hinweise
3.
Konstruktion der orthogonalen Axonometrie
3.0. Ziehen Sie vom Transparent 2 die verschiedenen
Bilder der Koordinatenachsen auf ein Transparent
DIN A2 durch.
3.1. Ziehen Sie den Grundriss des Gebäudes durch.
3.2. Ziehen Sie den Aufriss des Gebäudes durch.
3.3. Konstruieren Sie die orthogonale Axonometrie des
Hochhauses mit Hilfe des Einschneideverfahrens.
3.4. Ziehen Sie die sichtbaren Kanten des Gebäudes
nach.
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
Transparent 3 – Lösungsweg 2 : Einscheideverfahren
2.5 Übung
Seite
7
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
2.5 Übung
Seite
8
Lösungsweg 3 : Rechnereinsatz
Transparent 1 – Hinweise
1.
Entwurf
1.1. Entwerfen Sie das Hochhaus.
1.2. Geben Sie Ihren Entwurf als 3D-Modell in den
Rechner ein.
1.3. Erstellen Sie ein Layout für die Darstellung von
Grundriss und Aufriss.
1.4. Drucken Sie Grundriss und Aufriss aus.
Transparent 2 – Hinweise
2.
Orthogonale Axonometrie
2.1. Legen Sie eine günstige Blickrichtung fest.
2.2. Speichern Sie die Einstellung (AXO-von-oben).
2.3. Exportieren Sie das Bild (2D-Drahtkörper, verdeckt) als wmf-Datei.
(>Datei>Exportieren>name.wmf)
2.4. Importieren Sie die wmf-Datei in das Layout.
(>Einfügen>WMF>name.wmf)
2.5. Geben Sie die Axonometrie für die entgegengesetzte
Blickrichtung ein, speichern Sie die Einstellung
(AXO-von-unten), erzeugen Sie eine wmf-Datei
und fügen Sie diese ins Layout ein.
2.6. Drucken Sie beide Axonometrien aus.
Transparent 3 – Hinweise Teil 1
3.
Rekonstruktion der orthogonalen Axonometrie
3.1. Zeichnen Sie die Bilder der Koordinatenachsen ein.
3.2. Ermitteln Sie ein Spurpunktdreieck für die
Axonometrie.
3.3. Konstruieren Sie durch Umklappung den Grundriss der Kooordinatenachsen.
Ermitteln und
beschriften Sie den horizontalen Winkel für die
Blickrichtung der Axonometrie.
3.4. Konstruieren Sie durch Umklappung den Seitenriss der Kooordinatenachsen. Ermitteln und
beschriften Sie den Neigungswinkel für die Blickrichtung der Axonometrie.
Transparent 3 – Hinweise Teil 2
3.5. Rekonstruieren Sie den Grundriss des Gebäudes.
3.6. Rekonstruieren Sie den Aufriss des Gebäudes.
Ermitteln und beschriften Sie den horizontalen
Winkel für die Blickrichtung der Axonometrie.
Transparent 4 – Hinweise
4.
Perspektive auf eine horizontale Bildebene
4.1. Legen Sie eine günstige Perspektive auf eine
horizontale Bildebene fest.
4.2. Speichern Sie die Einstellung (pi-horizontal).
4.3. Exportieren Sie das Bild als wmf-Datei.
(>Datei>Exportieren>name.wmf)
4.4. Importieren Sie die wmf-Datei in das Layout.
(>Einfügen>WMF>name.wmf)
4.5. Erstellen Sie ein Layout für die Darstellung der
Perspektive.
4.6. Drucken Sie die Perspektive aus.
Abgabe:
Schicken Sie mir die Datei:
Adresse: [email protected]
Betreff: DGIII Übung 1
Dateiname: DG-1vorname
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
Transparent 3 – Teil 1 (Lösungsweg 3 : Rechnereinsatz)
2.5 Übung
Seite
9
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
Transparent 3 – Teil 2 (Lösungsweg 3 : Rechnereinsatz)
2.5 Übung
Seite
10
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
Exkurs: Abbildung eines Kreiszylinders
2.5 Übung
(konjugierte Durchmesser einer Ellipse)
Seite
11
Darstellende Geometrie für Architekten III
Institut für Geometrie und Prakt. Mathematik – RWTH Aachen
2.5 Orthogonale Axonometrie
Exkurs: Abbildung eines Kreiszylinders
2.5 Übung
(Hauptachsen der Ellipsen)
Seite
12