Nichtlineare Dielektrika

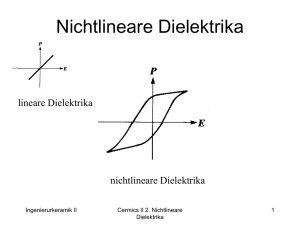
Nichtlineare Dielektrika
lineare Dielektrika
nichtlineare Dielektrika
Ingenierurkeramik II
2. Nichtlineare Dielektrika
1
Nichtlineare Dielektrika
•
grosse Dielektrizitätskonstante
•
spontane Polarisation unterhalb Tc
•
•
kristallographischen Phasenumwandlung
Dipole wechselwirken und richten sich in
Bezirken (Domänen) parallel aus → Polarisation
•
elektrisches Feld kann die Dipole
(die Domänen) in bestimmte Richtungen ausrichten
P
→ Ferroelektrika
Ingenierurkeramik II
E
2. Nichtlineare Dielektrika
2
BaTiO3-Bariumtitanat - der Prototyp
ferroelektrischer Keramiken
Ba, Pb und Sr weiten wegen ihrer Grösse
das kfz-Gitter auf → das Ti4+-Ion ist an der
unteren Grenze der Stabilität in der
oktaedrischen Position, d.h. das Ti4+-Ion
(r[Ti4+] = 0.61Å) ist fast zu klein für diese
Oktaederlücke (Radienverhältnis: ri : ra =
0.414 - 0.732).
Die kubische Elementarzelle von
Bariumtitanat. Ba-Ionen sitzen
auf den Ecken der Einheitszelle,
Ti im Zentrum des
Sauerstoffoktaeders.
Ingenierurkeramik II
Hier ri : ra = 0.44
2. Nichtlineare Dielektrika
3
Einheitszelle von PZT
Ingenierurkeramik II
2. Nichtlineare Dielektrika
4
•
•
BaTiO3-Bariumtitanat 2
Folge des zu kleinen Ti4+:
Bei hoher T starke Bewegung des Ti4+-Ion um die Gleichgewichtsposition:
→ kubische Symmetrie. Keine Polarisation!
•
Bei T<130°C → zwei Minima im Potentialtopf des Ti4+-Ions.
→ Einheitszelle wird teragonal verzerrt. Polarisation!
Phasenumwandlungen:
kubisch → tetragonal → orthorhombisch → rhomboedrisch
Ingenierurkeramik II
2. Nichtlineare Dielektrika
5
BaTiO3-Bariumtitanat-3
Ingenierurkeramik II
2. Nichtlineare Dielektrika
6
Kopplung der Dipole → Nettodipolmoment
eines Bereichs → Domäne.
Diese spontane Polarisation P, d.h. Ausrichten der Dipole ohne
äussere Einwirkungen, kann nur entlang bestimmter
kristallographischer Richtungen auftreten.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
7
90°- und 180°-Domänen
Bei BaTiO3 richten sich die Dipole in der:
•
tetragonalen Phase spezifisch entlang jeder [100]-Achse aus → nur 90°- und 180°Domänen bilden sich aus.
•
orthorhombischen Phase in 12 gleichwertige Sättigungspolarisationsrichtungen entlang
<110>.
•
rhomboedrische Phase parallel zu den <111>-Richtungen.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
8
Das CurieWeiss Gesetz: Einfluss der T auf die
Polarisation von BaTiO3
Oberhalb TC verliert sich die
spontane Polarisation. Die
thermische Bewegung wirkt
gegen die Ordnung der Dipole
und die einzelnen
Dipolmomente werden kleiner.
Die spontane Polarisation
verschwindet wieder.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
9
Beschreibung der Ferroelektrika
„Polarisationskatastrophe“.
Bei einer Polarisationskatastrophe nimmt das von der Polarisation hervorgerufene
lokale elektrische Feld schneller zu als die elastische Rückstellkraft für ein Ion im
Kristall und führt dadurch zu einer asymmetrischen Verschiebung der Ionen.
P= (er-1) e0 E
(1.10)
P= E locSNi ai
P
(1.14)
mit Eloc= E+P/3e0
und SNi ai= N ao
Na 0
Für:
1
3e 0
Ingenierurkeramik II
E  Na 0

Na 0 
1 

3e 0 

Na 0
geht
e0
e r 1 

 
 Na 0 
1 

3e 0 

2. Nichtlineare Dielektrika
10
Einfluss der T auf die spontane Polarisation
Oberhalb Tc, also im paraelektrischen Zustand, gilt in der Nähe
der Umwandlungstempeeratur das Curie-Weiss-Gesetz:
Relative Permitivity
C
er 
T  TC
Tc
Temperature °C
Übergang vom ferroelektrischen in den paraelektrischen Zustand. Ein Ferroelektrika
ist oberhalb Tc ein lineares und unterhalb Tc ein nichtlineares Dielektrikum.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
11
Dielektrizitätskonstante für den paraelektrischen
Zustand
Ingenierurkeramik II
2. Nichtlineare Dielektrika
12
Mischkristalle 1
Durch Mischkristallbildung unter den Perowskiten können die verschiedenen
Umwandlungstemperaturen über grosse Bereiche verschoben werden: (BaTiO3-PbTiO3).
kub.
tetr.
morphotrophe
Phasengrenze
BaTiO3
PbTiO3
Morphotrope Phasengrenze (fast unabhängig von T) bei
45% PbTiO3
Ingenierurkeramik II
2. Nichtlineare Dielektrika
13
Mischkristalle 2: BaTiO3
Ingenierurkeramik II
2. Nichtlineare Dielektrika
14
Ferroelektrische Oxide
Zusammensetzung
LiNbO3
NaNbO3
KNbO3
Pb(0.5Sc0.5Nb)O3
Pb(0.33Mg0.67Nb)O3
Pb(0.33Zn0.67Nb)O3
LiTaO3
PbTa2O6
Pb(0.5Fe0.5Ta)O3
SrBi2Ta2O9
Sm(MoO4)3
Eu2(MoO4)3
Pb5GeO11
SrTeO3
Ingenierurkeramik II
Tc [°C]
Ps [mC/cm2]
1210
-200
435
90
-8
140
665
260
-40
335
197
180
178
485
2. Nichtlineare Dielektrika
71
12
30.3
3.6
24
24
50
10
28
5.8
0.24
0.14
4.6
3.7
bei T [°C]
23
-200
250
18
-170
125
25
25
170
25
50
25
25
312
15
Einfluss eines äusseren elektrischen Feldes
Bei T>Tc : grosse Auslenkung für das Ti4+-Ion im äusseren elektrischen
→
Feld:
Kristall wird polarisiert.
Bei Feld E=0 springt das Ti4+-Ion wieder in seine zentrosymmetrische
Lage
→ Polarisation =0: paraelektrisch
Polung eines Ferroelektrischen Werkstoffes:
Bei T<Tc : spontane Ausrichtung der Dipolmomente. Ein äusseres Feld E richtet
die kann die Domänen durch Verschieben der Domänenwände aus.
In der tetragonalen Phase ist die Umpolarisation von 90°- und 180°-Domänen
möglich. Im Falle des Umklappens einer 180°-Domäne braucht das Ti4+-Ion nur
von der einen stabilen Lage in die andere zu springen. Die Elementarzelle
verändert sich nicht. Das Ausrichten von 90°-Domänen bedingt aber auch eine
Umorientierung der tetragonalen Einheitszelle um 90°, d.h. die ursprüngliche cAchse wird zur a-Achse gestaucht, während eine a-Achse auf die Länge der cAchse gestreckt werden muss.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
16
Einfluss eines äusseren elektrischen Feldes-2
•
•
Nach der Herstellung eines Ferroelektrischen Bauteils sind die Orientierungen der
Polarisationen aller Domänen gleichverteilt. Das Bauteil zeigt daher kein
makroskopisches Dipolmoment.
Durch anlegen eines elektrischen Feldes können die vorgefertigten Dipolmomente
der einzelnen Domänen in Feldrichtung ausgerichtet werden. Die Ausrichtung
erfolgt durch Umklappprozesse und dann gegen die thermische Bewegung (siehe
zeitliches und thermisches Problem der Orientierungspolarisation).
Ingenierurkeramik II
2. Nichtlineare Dielektrika
17
Einfluss eines äusseren elektrischen Feldes-3
Ferroelektrische Hysterese
Ingenierurkeramik II
2. Nichtlineare Dielektrika
18
Antiferroelektrika: PbZrO3
PbZrO3
Benachbarte Ketten von Elementarzellen antiparallel zueinander orientiert. Es bestehen
zwei antiparallel polarisierte Untergitter und die makroskopisch gemessene Polarisation ist
Null
Für E>Ek
Ek
Ingenierurkeramik II
2. Nichtlineare Dielektrika
19
Ferroelektrische Keramik
a)
b)
Der Einkristall (a) lässt sich vollständig in der Richtung des äusseren Feldes polarisieren. Dies
erlaubt eine stärkere Polarisation des Einkristalles.
Im Vergleich zur Keramik (b), bei der eine statistische Verteilung der Körner vorliegt.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
20
Spontane Polarisation von
Perowskiten
Einkristall
Ps
[mC/cm2]
BaTiO3
27
PbTiO3
75
KNbO3
30
LiTaO3
50
Keramik
Ps
[mC/cm2]
BaTiO3
8
PZT56
47
PZT93
35
PLZT
45
Ingenierurkeramik II
2. Nichtlineare Dielektrika
Pb2FeNbO6
16
21
Einfluss der Korngrösse
Bei Korngrössen von 1mm oder weniger sind die Körner verzwillingt, eindomänig und neigen
zunehmend zur kubischen Symmetrie (paraelektrisch): die Phasenumwandlung kubischtetragonal wird unterdrückt. Unterhalb einer Grösse von ca. 1mm werden die ferroelektrischen
Anomalien fast völlig unterdrückt.
Mit steigender Korngrösse wird
andererseits das Gefüge zu starr;
beim Polarisieren entstehen
Spannungen, und die Domänen
gehen nach Abschalten des Feldes
teilweise in ihre Ausgangslagen
zurück. Keramiken mit grossen
Körnern lassen sich daher schwerer
polarisieren.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
22
Eigenschaften ferroelektrischer
keramischer Werkstoffe
•
Hohe Dielektrizitätskonstante
•
Relativ geringe dielektrische Verluste
•
Hohe Piezoelektrizitätskonstante
•
Rel. hoher elektrischer Widerstand
•
Feuchtigkeitsempfindlichkeit
•
Elektromagnetische Kopplung
•
Hohe pyroelektrische Koeffizienten
•
Teilweise optische Transparenz
•
Hohe elektrooptische Koeffizienten
Ingenierurkeramik II
2. Nichtlineare Dielektrika
23
Zusammenfassung
•
•
•
•
Bariumtitanat (und viele andere Perowskite) → spontane Polarisation
Tc. Bei Perowskiten einstellbar durch Mischkristallbildung.
>Tc: kubische paraelektrische Phase
Durch E-Feld lässt sich das Material polarisieren. Beim Abschalten des Feldes
verschwindet die Polarisation wieder. Es sind keine Dipole vorhanden. Curie-Weiss-Gesetz
<Tc:spontane Verschiebung der Ladungsschwerpunkte entlang bestimmter
kristallographischer Achsen statt. Es bilden sich Dipole. Die Polarisationrichtungen der
einzelnen Domänen sind statistisch verteilt. Makroskopisch ist keine Polarisation
festzustellen. Durch ein äusseres E-Feld werden die Domänen ausgerichtet. Es bleibt eine
Nettopolarisation nach Abschalten des Feldes erhalten. Das Material ist ferroelektrisch.
Umpolarisierung von 90°-Domänen führt zu inneren Spannungen im polykristallinen
Werkstoff.
•
In polykristallinen Werkstoffen (Keramiken) wird die maximale Polarisation des Einkristalls
aufgrund der statistischen Ausrichtung der Körner nur teilweise erreicht.
•
Bei feinkörnigen Keramiken werden die Körner eindomänig und zunehmend wird die
Phasenumwandlung kubisch-tetragonal unterdrückt. Die ferroelektrischen Anomalien
werden fast vollständig unterbunden.
Ingenierurkeramik II
2. Nichtlineare Dielektrika
24
Piezomaterialien
Ingenierurkeramik II
2. Nichtlineare Dielektrika
25