1 Probe-Klausur zur Vorlesung „Einführung in die Informatik“, 05.07

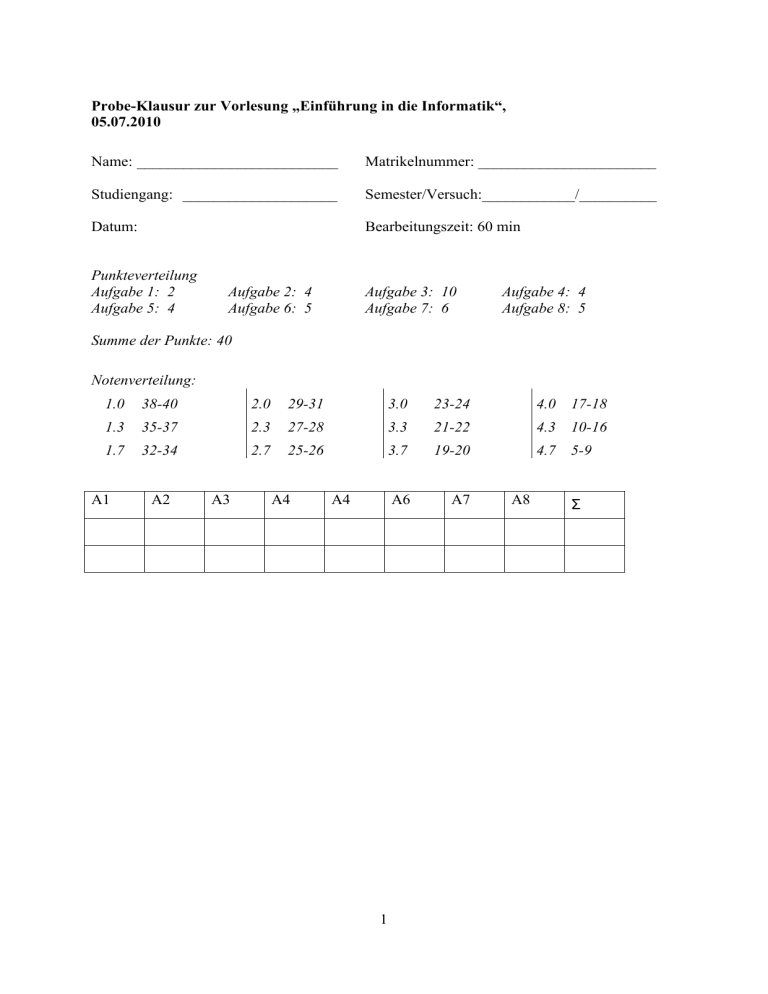
Probe-Klausur zur Vorlesung „Einführung in die Informatik“,
05.07.2010
Name: __________________________
Matrikelnummer: _______________________
Studiengang: ____________________
Semester/Versuch:____________/__________
Datum:
Bearbeitungszeit: 60 min
Punkteverteilung
Aufgabe 1: 2
Aufgabe 5: 4
Aufgabe 2: 4
Aufgabe 6: 5
Aufgabe 3: 10
Aufgabe 7: 6
Aufgabe 4: 4
Aufgabe 8: 5
Summe der Punkte: 40
Notenverteilung:
1.0
38-40
2.0
29-31
3.0
23-24
4.0 17-18
1.3
35-37
2.3
27-28
3.3
21-22
4.3 10-16
1.7
32-34
2.7
25-26
3.7
19-20
4.7 5-9
A6
A7
A1
A2
A3
A4
A4
1
A8
Σ
Aufgabe 1) Darstellung von Grafiken (2 Punkte)
In digitalen Rechensystemen können Abbildungen auf zwei verschiedene Arten realisiert
werden.
a) Was versteht man unter Vektorgrafik?
(1 Punkt)
b) Was versteht man unter Rastergrafik?
(1 Punkt)
Aufgabe 2) Lineare Suche (4 Punkte)
Angenommen, B sei eine Reihung mit n Elementen. Die Elemente B1, ..., Bn haben als Werte
jeweils Zahlen. In der Reihung B soll nach einem Element mit dem Wert 35 gesucht werden.
a) Beschreiben Sie den Algorithmus zur linearen (und nicht der binären!) Suche, um in
der Reihung B nach einem Element mit dem Wert 35 zu suchen.
(2 Punkte)
b) Skizzieren Sie kurz Vorteile und Nachteile der linearen Suche (z. B. gegenüber der binären Suche)?
(2 Punkte)
2
Aufgabe 3) Datenbanken (10 Punkte)
Eine Universität möchte in einer relationalen Datenbank Informationen zu Vorlesungen, Dozenten, Studierenden und Studiengängen sowie die Beziehungen zwischen diesen Informationen verwalten. Zunächst wird ein ER-Modell (Entity-Relationship Modell) erstellt. Es existieren dabei die Entity-Typen
Studierender: mit den Attributen: Name, MatrikelNr, Geburtsdatum
Studiengang: mit den Attributen: Name, Kürzel, Fakultät
Dozent: mit den Attributen: PersonalNr, Name
Vorlesung: mit den Attributen: VorlesungsID, Name, ECTS, Kurzbeschreibung
und die Relationship-Typen
besucht: zwischen Studierender und Vorlesung
studiert: zwischen Studierender und Studiengang
hält: zwischen Dozent und Vorlesung
zugeordnet: zwischen Vorlesung und Studiengang
Beachten Sie folgende Festlegungen:
-
Ein Studierender besucht mehrere Vorlesungen; eine Vorlesung wird von mehreren
Studierenden besucht.
-
Ein Dozent kann mehrere Vorlesungen halten; eine Vorlesung wird von einem Dozenten gehalten.
-
Ein Studiengang umfasst eine Reihe von Vorlesungen; eine Vorlesung kann mehreren
Studiengängen zugeordnet sein.
-
Ein Studierender ist für einen Studiengang eingeschrieben; ein Studiengang wird von
vielen Studierenden studiert.
Teilaufgaben
a) Zeichnen Sie für diese Datenbankaufgabe das zugehörige ER-Modell. Geben sie für
jeden Entity-Typ einen geeigneten Primärschlüssel und bei den Relationship-Typen
die zugehörigen Kardinalitäten an.
(8 Punkte)
b) Das ER-Modell der Teilaufgabe a) soll nun in Tabellen der relationalen Datenbank
umgesetzt werden. Jeder Entity-Typ wird dabei auf eine eigene Tabelle abgebildet
(d.h. es entstehen die Tabellen Studierender, Studiengang, Dozent und Vorlesung).
Bilden Sie nun die folgenden Relationship-Typen der Teilaufgabe a) auf Tabellen
der relationalen Datenbank ab:
•
„studiert“
•
„besucht“
Beachten Sie dabei die Kardinalitäten der Relationship-Typen, um entscheiden zu
können, ob für den jeweiligen Relationship-Typ eine eigene Tabelle notwendig ist
oder nicht.
(2 Punkte)
3
Aufgabe 4) Algorithmus, Programm, Prozess (4 Punkte)
a) Charakterisieren Sie kurz die Begriffe Algorithmus, Programm und Prozess.
(3 Punkte)
b) Welche Zustände kann ein Prozess einnehmen?
(1 Punkt)
Aufgabe 5) Rekursion (4 Punkte)
Das Wachstum einer Kaninchenpopulation kann über die Fibonacci-Folge beschrieben werden. Eine Zahl der Fibonacci-Folge berechnet sich durch die Addition der beiden vorherigen
Zahlen der Folge (0, 1, 1, 2, 3, 5, 8, 13, …). Die formale rekursive Definition der FibonacciFolge lautet:
a) Ergänzen Sie die nachfolgende Java-Methode computeNthFibonacciNumber so, dass
die Funktion die n-te Zahl der Fibonacci-Folge zurückgibt. (2P)
public class Fibonacci {
public int computeNthFibonacciNumber(int n){
int result = 0;
if(n == 0){
result = 0;
} else if(n == 1){
result = 1;
} else {
result = computeNthFibonacciNumber(n - 1) + computeNthFibonacciNu
}
return result;
}
}
b) Wenn die Methode mit
Fibonacci someFibonacci = new Fibonacci();
someFibonacci.computeNthFibonacciNumber(4);
aufgerufen wird:
Wie entfaltet sich dann die Rekursion als Folge von Aufrufen? Für die Darstellung der
Folge der Aufrufe können Sie entweder eine textuelle oder eine graphische Darstellung
verwenden. (2P)
4
Aufgabe 6) Java (5 Punkte)
Es soll ein simpler Taschenrechner in Java programmiert werden. Der Taschenrechner soll
zwei Funktionen haben:
• Addieren von positiven natürlichen Zahlen (einschließlich 0) und
• Exponenzieren positiver natürlicher Zahlen mit positiven natürlichen Exponenten (jeweils einschließlich 0).
Hierzu seien die folgende Klasse Calculator gegeben. Füllen Sie die Lücken geeignet mit Java-Elementen (Ausdrücke, Klammern etc.)!
Lösung:
public class Calculator {
public long addNumbers(long numberOne, long numberTwo){
long result = numberOne + numberTwo;
return result;
}
public long exponentiateNumbers(long base, long exponent){
long result = 1;
for(int i=0; i < exponent; i++){
result = result * base;
}
return result;
}
}
Aufgabe 7) Normalform (6 Punkte)
a) Erklären Sie in Stichpunkten die 2. Normalform (1 P.)
b) Würde man die nachfolgende Relation verwenden, kann es zu Anomalien kommen.
Welche Anomalien können auftreten? Geben Sie ein Beispiel je Anomalie an. (3 P)
SchülerId
Name
Wohnort
Geschlecht
Geburtsjahr
KlassenId
Klassenzimmer
32134234883
9
Meier, Franz
80333 München
männlich
1987
9a
234
68742364987
3
Gebhardt,
Doris
80333 München
weiblich
1985
7c
Pavillon
…
…
…
…
…
…
…
5
c) Modifizieren Sie die Tabelle aus Teilaufgabe 7 b in der Weise, dass die ersten drei
Normalformen erfüllt sind. Es genügt, wenn Sie die neue(n) Tabelle(n) ohne Datentupel angeben. (2P)
6
Aufgabe 8) SQL (5 Punkte)
Ein Gymnasium setzt eine Datenbank ein, um die Noten der Schüler zu erfassen. Insbesondere werden die Noten der mündlichen Abiturprüfung in der Relation „prüfen“ gespeichert. Gehen sie von folgender Beispielausprägung der Datenbank aus:
Schüler
Lehrer
LehrerId
Nachname
Vorname
SchülerId Nachname
Vorname
23
Meier
Paul
150
Axt
Simon
24
Schmidt
Eva
151
Gerull
Alex
25
Eckhardt
Max
152
Huber
Karin
26
Hussak
Susi
153
Scholl
Benni
27
Walter
Hans
154
Zeiler
Ena
155
Klug
Anna
prüfen
Fach
SchülerId FachId
LehrerId Note
FachId
Bezeichnung
153
10
23
3
10
Mathe
154
10
26
1
11
Physik
152
13
25
2
12
Deutsch
150
12
27
4
13
Erdkunde
151
14
24
3
14
Englisch
Formulieren Sie nachfolgende SQL-Anfragen:
a) Finden Sie den Nach- und Vornamen von Schülern, die bei Frau Hussak eine 1 bekommen haben. (3P)
b) Die Schülerin Anna Klug hat soeben ihre mündliche Abiturprüfung im Fach Physik
bei Herrn Walter mit Note 3 bestanden. Geben Sie einen SQL Ausdruck an, durch den
die Ausprägung der Datenbank entsprechend der neuen Situation modifiziert wird.
(2P)
ENDE DER KLAUSURAUFGABEN
7
Lösung zu den Aufgaben, Wiederholungsklausur WS 2009/10
Aufgabe 1) Darstellung von Grafiken (2 Punkte)
In digitalen Rechensystemen können Abbildungen auf zwei verschiedene Arten realisiert
werden.
c) Was versteht man unter Vektorgrafik?
(1 Punkt)
d) Was versteht man unter Rastergrafik?
(1 Punkt)
Lösung
Lösung zu Teilaufgabe a) (1 Punkt)
Eine Vektorgraphik besteht aus einer Menge von geometrischen Objekten, wie z.B. Linie, Rechteck. Vektorgraphiken sind geeignet für Zeichnungen. Vektorgrafiken benötigen erheblich weniger Speicher.
Lösung zu Teilaufgabe b) (1 Punkt)
Rastergraphiken bestehen aus einer Menge von Pixeln. Rastergraphiken sind geeignet
für die Darstellung von Fotos, z.B. von Digitalkameras.
Aufgabe 2) Lineare Suche (4 Punkte)
Angenommen, B sei eine Reihung mit n Elementen. Die Elemente B1, ..., Bn haben als Werte
jeweils Zahlen. In der Reihung B soll nach einem Element mit dem Wert 35 gesucht werden.
c) Beschreiben Sie in einfachen Worten den Algorithmus zur linearen (und nicht der binären!) Suche, um in der Reihung B nach einem Element mit dem Wert 35 zu suchen.
(2 Punkte)
d) Skizzieren Sie kurz Vorteile und Nachteile der linearen Suche (z. B. gegenüber der binären Suche)?
(2 Punkte)
Lösung zu Teilaufgabe a) (2 Punkte)
Man durchsucht die Reihung sequentiell, ein Element nach dem anderen, solange bis
man das Element mit Wert 35 gefunden hat. Man gibt das gefundene Element zurück,
der Algorithmus stoppt.
(Man kann auch eine Beschreibung in Java oder Pseudocode angeben.)
Lösung zu Teilaufgabe b) (2 Punkte)
Vorteil: bei der linearen Suche muss die Zahlenmenge nicht sortiert sein, während die
binäre Suche eine sortiere Zahlenmenge erwartet. (1 Punkt)
8
Nachteil: im schlimmsten Fall muss die gesamte Zahlenmenge durchsucht werden;
auch um festzustellen ob die Zahl in der Zahlenmenge enthalten ist oder nicht. (1
Punkt)
9
Aufgabe 3) Datenbanken (10 Punkte)
Eine Universität möchte in einer relationalen Datenbank Informationen zu Vorlesungen, Dozenten, Studierenden und Studiengängen sowie die Beziehungen zwischen diesen Informationen verwalten. Zunächst wird ein ER-Modell (Entity-Relationship Modell) erstellt. Es existieren dabei die Entity-Typen
Studierender: mit den Attributen: Name, MatrikelNr, Geburtsdatum
Studiengang: mit den Attributen: Name, Kürzel, Fakultät
Dozent: mit den Attributen: PersonalNr, Name
Vorlesung: mit den Attributen: VorlesungsID, Name, ECTS, Kurzbeschreibung
und die Relationship-Typen
besucht: zwischen Studierender und Vorlesung
studiert: zwischen Studierender und Studiengang
hält: zwischen Dozent und Vorlesung
zugeordnet: zwischen Vorlesung und Studiengang
Beachten Sie folgende Festlegungen:
-
Ein Studierender besucht mehrere Vorlesungen; eine Vorlesung wird von mehreren
Studierenden besucht.
-
Ein Dozent kann mehrere Vorlesungen halten; eine Vorlesung wird von einem Dozenten gehalten.
-
Ein Studiengang umfasst eine Reihe von Vorlesungen; eine Vorlesung kann mehreren
Studiengängen zugeordnet sein.
-
Ein Studierender ist für einen Studiengang eingeschrieben; ein Studiengang wird von
vielen Studierenden studiert.
Teilaufgaben
a) Zeichnen Sie für diese Datenbankaufgabe das zugehörige ER-Modell. Geben sie für
jeden Entity-Typ einen geeigneten Primärschlüssel und bei den Relationship-Typen
die zugehörigen Kardinalitäten an.
(8 Punkte)
b) Das ER-Modell der Teilaufgabe a) soll nun in Tabellen der relationalen Datenbank
umgesetzt werden. Jeder Entity-Typ wird dabei auf eine eigene Tabelle abgebildet
(d.h. es entstehen die Tabellen Studierender, Studiengang, Dozent und Vorlesung).
Bilden Sie nun die folgenden Relationship-Typen der Teilaufgabe a) auf Tabellen
der relationalen Datenbank ab:
•
„studiert“
•
„besucht“
Beachten Sie dabei die Kardinalitäten der Relationship-Typen, um entscheiden zu
können, ob für den jeweiligen Relationship-Typ eine eigene Tabelle notwendig ist
oder nicht.
(2 Punkte)
10
Lösung zu Teilaufgabe a) (8 Punkte)
1 Punkt
1 Punkt
MatrikelNr
Name
Geburtsdatum
1 Punkt
Studierender
N
besucht
M
N
1 Punkt
M
studiert
zugeordnet
1
Name
Kürzel
Fakultät
Studiengang
Vorlesung
1 Punkt
N
N
hält
VorlesungsID
Name
Kurzbeschreibung
ECTS
1 Punkt
1
Dozent
PersonalNr
Name
1 Punkt
1 Punkt
Die Primärschlüssel der Entity-Typen sind die Folgenden:
Studierender: MatrikelNr
Studiengang: Name
Vorlesung: VorlesungsID
Dozent: PersonalNr
Lösung zu Teilaufgabe b) (2 Punkte)
Es erfolgt folgende Umsetzung der Relationship-Typen
„studiert“ (Kardinalität 1:N) wird in Tabelle Studierender integriert, wobei Name als
Fremdschlüssel aufgenommen wird.
(1 Punkt)
„besucht“ (Kardinalität M:N) wird als eigene Tabelle „besucht“ realisiert, deren Primärschlüssel aus den beiden Attributen MatrikelNr und VorlesungsID besteht. (1 Punkt)
11
Aufgabe 4) Algorithmus, Programm, Prozess (4 Punkte)
a) Charakterisieren Sie kurz die Begriffe Algorithmus, Programm und Prozess.
(3 Punkte)
b) Welche Zustände kann ein Prozess einnehmen?
(1 Punkt)
Lösung
Lösung zu Teilaufgabe a) (3 Punkte)
-
Ein Algorithmus ist eine detaillierte und explizite Vorschrift zur schrittweisen Lösung eines Problems.
(1 Punkt)
Oder Ein Algorithmus ist eine endliche, deterministische und effektive Vorschrift.
-
Ein Programm ist die Formulierung eines Algorithmus in einer Programmiersprache.
(1 Punkt)
-
Ein Prozess ist die Ausführung eines Programms in einem Rechner.
Lösung zu Teilaufgabe b)
Prozesse können die folgenden Zustände einnehmen:
„wartend“ (waiting), „bereit“ (ready) oder „laufend“ (running))
12
(1 Punkt)
Aufgabe 5) Rekursion (4 Punkte)
Das Wachstum einer Kaninchenpopulation kann über die Fibonacci-Folge beschrieben werden. Eine Zahl der Fibonacci-Folge berechnet sich durch die Addition der beiden vorherigen
Zahlen der Folge (0, 1, 1, 2, 3, 5, 8, 13, …). Die formale rekursive Definition der FibonacciFolge lautet:
a) Ergänzen Sie die nachfolgende Java-Methode computeNthFibonacciNumber so, dass
die Funktion die n-te Zahl der Fibonacci-Folge zurückgibt. (2P)
public class Fibonacci {
public int computeNthFibonacciNumber(int n){
int result = 0;
if(n == 0){
result = 0;
} else if(n == 1){
result = 1;
} else {
result = computeNthFibonacciNumber(n - 1) + computeNthFibonacciNu
}
return result;
}
}
b) Wenn die Methode mit
Fibonacci someFibonacci = new Fibonacci();
someFibonacci.computeNthFibonacciNumber(4);
aufgerufen wird:
Wie entfaltet sich dann die Rekursion als Folge von Aufrufen? Für die Darstellung der
Folge der Aufrufe können Sie entweder eine textuelle oder eine graphische Darstellung
verwenden. (2P)
Lösung
Lösung zur Teilaufgabe 2 a) (2 Punkte):
public class Fibonacci {
public int computeNthFibonacciNumber(int n){
int result = 0;
if(n == 0){
result = 0;
} else if(n == 1){
result = 1;
} else {
result = computeNthFibonacciNumber(n-1) + computeNthFibonacciNumber(n-2);
}
13
return result;
}
}
Lösung zur Teilaufgabe 2 b) (2 Punkte)
Textuell:
Kürzen wir zur Notation den Methodenaufruf computeNthFibonacciNumber(int n) mit fibo(n) ab, so erhalten wir: fibo(4) = fibo(2) + fibo(3)
= fibo(0) + fibo(1) + fibo(1) + fibo(2)
= fibo(0) + fibo(1) + fibo(1) + fibo(0) + fibo(1)
=0+1+1+0+1
Graphisch:
fibo(4)
fibo(3)
fibo(2)
fibo(0)
0
fibo(1)
fibo(1)
1
1
fibo(2)
fibo(0)
0
14
fibo(1)
1
Aufgabe 6) Java (4 Punkte)
Es soll ein simpler Taschenrechner in Java programmiert werden. Der Taschenrechner soll
zwei Funktionen haben:
• Addieren von positiven natürlichen Zahlen (einschließlich 0) und
• Exponenzieren positiver natürlicher Zahlen mit positiven natürlichen Exponenten (jeweils einschließlich 0).
Hierzu seien die folgende Klasse Calculator gegeben. Füllen Sie die Lücken geeignet mit Java-Ausdrücken!
Lösung:
public class Calculator {
public long addNumbers(long numberOne, long numberTwo){
long result = numberOne + numberTwo;
return result;
}
public long exponentiateNumbers(long base, int exponent){
long result = 1;
for(int i=0; i < exponent; i++){
result = result * base;
}
return result;
}
}
Aufgabe 7) Normalform 6 Punkte)
a) Erklären Sie in Stichpunkten die 2.. Normalform (1 P.)
Eine Relation R mit zugehörigen funktionalen Abhängigkeiten F ist in 2. NF, falls jedes Nichtschlüsselattribut A ∈ R voll funktional abhängig ist von jedem Kandidatenschlüssel der Relation.
b) Würde man die nachfolgende Relation verwenden, kann es zu Anomalien kommen.
Welche Anomalien können auftreten? Geben Sie ein Beispiel je Anomalie an. (3 P)
15
SchülerId
Name
Wohnort
Geschlecht Geburtsjahr
KlassenId
Klassenzimmer
321342348839
Meier,
Franz
80333
München
männlich
1987
9a
234
687423649873
Gebhardt,
Doris
80333
München
weiblich
1985
7c
Pavillon
…
…
…
…
…
…
…
Einfügeanomalie: Was macht man mit Schülern die noch keiner Klasse zugeordnet
wurden.
Updateanomalie: Würde man die Postleitzahlen für München ändern, dann müsste
man dies in allen Tupeln tun die Schüler in München repreäsentieren.
Löschanomalie: Was passiert wenn das Pavillon als Klassenzimmer nicht mehr zur
Verfügung steht da es abgerissen wurde. Ein Löschen der Tupel mit Pavillon als Klassenzimmer würde den Verlust von Schülerinformationen implizieren.
b) Modifizieren Sie die Tabelle aus Teilaufgabe 7 b in der Weise, dass die ersten drei
Normalformen erfüllt sind. Es genügt, wenn Sie die neue(n) Tabelle(n) ohne Datentupel angeben. (2P)
Schüler
SchülerId KlassenId Nachname Vorname PLZ
(0,5P)
Klasse
KlassenId Klassenzimmer
(0,5P)
PLZ
Ort
(1P)
16
Geschlecht
Geburtsjahr
Aufgabe 8) SQL (5 Punkte)
Ein Gymnasium setzt eine Datenbank ein, um die Noten der Schüler zu erfassen. Insbesondere werden die Noten der mündlichen Abiturprüfung in der Relation „prüfen“
gespeichert. Gehen sie von folgender Beispielausprägung der Datenbank aus:
Schüler
Lehrer
LehrerId
Nachname
Vorname
SchülerId Nachname
Vorname
23
Meier
Paul
150
Axt
Simon
24
Schmidt
Eva
151
Gerull
Alex
25
Eckhardt
Max
152
Huber
Karin
26
Hussak
Susi
153
Scholl
Benni
27
Walter
Hans
154
Zeiler
Ena
155
Klug
Anna
prüfen
Fach
SchülerId FachId
LehrerId Note
FachId
Bezeichnung
153
10
23
3
10
Mathe
154
10
26
1
11
Physik
152
13
25
2
12
Deutsch
150
12
27
4
13
Erdkunde
151
14
24
3
14
Englisch
Formulieren Sie nachfolgende SQL-Anfragen:
a) Finden Sie den Nach- und Vornamen von Schülern, die bei Frau Hussak eine 1 bekommen haben. (3P)
select s.Nachname, s.Vorname
from Schüler s, Lehrer l, prüfen p
where l.Nachname = ’Hussak’
and l.LehrerId = p.LehrerId
and p.Note = 1
and p.SchülerId = s.SchülerId;
(Jede Zeile 0,5 Punkte -> 3 P. insgesamt)
b) Die Schülerin Anna Klug hat soeben ihre mündliche Abiturprüfung im Fach Physik
bei Herrn Walter mit Note 3 bestanden. Geben Sie einen SQL Ausdruck an, durch den
17
die Ausprägung der Datenbank entsprechend der neuen Situation modifiziert wird.
(2P)
INSERT INTO prüfen (SchülerId, FachId, LehrerId, Note.)
VALUES (155, 11, 27, 1);
(Jede Zeile 1 Punkt -> 2 P. insgesamt)
18