Zusammenfassung 6 3. Wurzel
Werbung
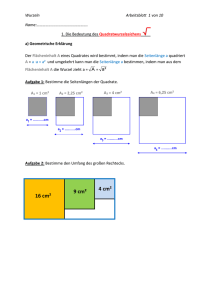
Zusammenfassung 6 3. Wurzel Aus den kleinen Würfeln soll ein großer Würfel gebaut werden. Wie viele kleine Würfel würdest du ver­ wenden – 26; 27 oder 28? Aus 125 kleinen Würfeln soll ein großer Würfel gebildet werden. Geht das? Du hast 1000 kleine Würfel zur Verfü­ gung. Wie viele verschiedene, aus kleinen Würfeln zusammengesetzte große Würfel lassen sich bauen? Zahlen der Form a 3 wie z. B. 5 · 5 · 5 = 5 3 = 125 heißen Kubikzahlen. Will man umgekehrt zu einer vorgegebenen Kubikzahl die Zahl bestimmen, die dreimal mit sich selbst multipliziert wieder die Kubikzahl__ ergibt, sucht man die 3. Wurzel oder die 3 Kubikwurzel der Zahl. √ 27 = 3; da 3 · 3 · 3 = 27. √____ 64 = 8; da 8 · 8 = 64 √__ 1,21 = 1,1; da 1,1 · 1,1 = 1,21 näherungsweise Bestimmung von Quadratwurzeln Von Quadratwurzeln aus positiven Zahlen, die keine Quadratzahlen sind, lassen sich durch Eingrenzung beliebig viele Nachkom­ maziffern bestimmen. Jede Eingrenzung heißt Intervall. √ 3 liegt im Intervall [1,7; 1,8], denn 2 < 3 < 1,8 2 1,7 __ √ 3 liegt im Intervall [1,73; 1,74], denn 1,73 2 < 3 < 1,74 2 Multiplikation und Division von Quadratwurzeln Quadratwurzeln kann man multiplizieren bzw. dividieren, indem man die Radikan­ den miteinander multipliziert bzw. dividiert und Wurzel zieht. __ die____ __ dann √ √__a · √ b = a · b a, b ≥ 0 __ a √ a __ _ = _b a ≥ 0, b > 0 √___ 7 · √ 28 = √ 196 = 14 ___√ 7 · 28 = Summen bzw. Differenzen, in denen Quadratwurzeln mit gleichen Radikanden vorkommen, können durch Ausklammern zusammengefasst werden. 5 √__ 3 + 2 √__ 3 = (5 +__2) √ 3 = 7 √ 3 8 √ 2 – 5 √ 2 = 3 √ 2 Beim teilweisen Wurzelziehen wird der Ra­ dikand so in ein Produkt zerlegt, dass einer der Faktoren__eine __Quadratzahl ist. _____ __ √ a 2 · b = √ a 2 · √ b = a · √ b mit a, b≥0 √ 175 = √ 25 · 7 = √ 25 · √ 7 = 5 · √ 7 Von Zahlen, die keine Kubikzahlen sind, lassen sich Kubikwurzeln näherungsweise bestim­ men. Durch Probieren gelangt man beispielsweise so zur Kubikwurzel der Zahl 50: 3 __ Wegen 3 3 < 50 < 4 3 liegt √ 50 zwischen 3 und 4; also im Intervall [3; 4]. 3 __ Wegen 3,6 3 < 50 < 3,7 3 liegt √ 50 zwischen 3,6 und 3,7; also im Intervall [3,6; 3,7]. 3 ____ √ 6859 Radikand Die Kubikwurzel einer positiven Zahl b ist die positive Zahl a, deren 3. Potenz __ 3 gleich der Zahl b ist: √ b = a, wenn a 3 = b und a, b ≥ 0. Beispiele 3 ___ a) √ 125 = 5; da 5 3 = 125 Bei Quadratwurzeln schreibt man den Wurzelexponenten in der Regel nicht: ___ 2 __ √ 49 = √ 49 . 3. Wurzel 3 ____ b) √ 0,343 = 0,7; da 0,7 3 = 0,343 teilweises ­Wurzelziehen Rationalmachen des Nenners √__9 3 3 9 3 _ _ _ _ _ 49 = å ; da å · å = 49 √ 0 = 0; da 0 · 0 = 0 __ ___ __ ___ _____ __ 112 __ _ √_ = 112 = √ 16 = 4 7 √ 7 √ √ __ ___ __ Eine Quadratwurzel im Nenner eines Bru­ ches lässt sich durch Erweitern beseitigen. __ __ _____ __ __ ___ ____ __ __ __ __ √ 5 · 2 √__5 2 √ 5 __ · √ 2 __ _ __ 2 = __ = 2 = √ 10 2 √ 2 √ 2 · √ 2 Aufgaben 1 Berechne im Kopf. 3 _ 3 __ 3 ___ a) √ ___ 8 b)√ ____ 64 c) √ ___ 216 3 3 3 d) √ ____ 343 e)√ ____ 1000 f) √ ____ 512 3 3 3 g) √ 0,001 h)√ 0,027 i) √ 0,125 3 3 4 Zwischen welchen natürlichen Zah­ len liegt die Kubikwurzel? Schätze__ zuerst. 3 __ 3 __ 3 a) √ ___ 20 b)√ ___ 60 c) √ ___ 90 3 3 3 d) √ 170 e)√ 300 f) √ 700 74 √ b Zusammenfassen von Quadratwurzeln Wurzelexponent ___ Die Quadratwurzel einer positiven Zahl b ist die positive Zahl a, die mit sich multipli­ 2 ziert wiederum die Zahl __ b ergibt: a = b. Schreibweise: a = √ b Diese Regel gilt auch für die Zahl Null. Quadratwurzel Berechne die Kubikwurzeln der Zahlen. Was fällt dir auf? a) 8; 80; 800; 8000; 80 000; 800 000 b) 0,027; 0,27; 2,7; 27; 270; 2700; 27 000 Ergänze. 3 __ a) √ ____ º = 3 3 c) √ _____ º 12 = 8 3 e) √ 64 + º = 5 3 Kubikwurzel Die Kubikwurzel einer positiven Zahl b ist die positive Zahl a, deren dritte Potenz gleich der Zahl b ist: __ 3 √ b = a; wenn a 3 = b a, b ≥ 0 3 ___ √ 343 = 7; da 7 3 = 343 __ b) √ _____ º = 12 3 d) √ _____ º 2 º = 9 3 f) √ 72 · º = 6 Zusammenfassung 75