Grundlagen der Theoretischen Informatik, WS10/11
Werbung
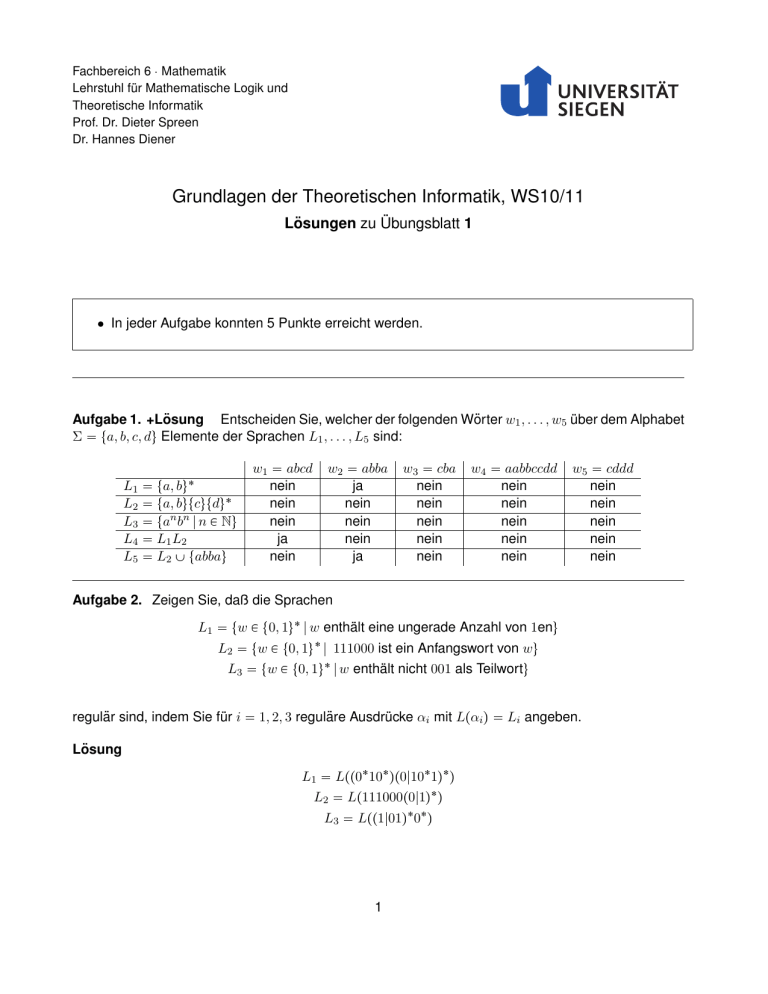
Fachbereich 6 Mathematik Lehrstuhl für Mathematische Logik und Theoretische Informatik Prof. Dr. Dieter Spreen Dr. Hannes Diener Grundlagen der Theoretischen Informatik, WS10/11 Lösungen zu Übungsblatt 1 • In jeder Aufgabe konnten 5 Punkte erreicht werden. Aufgabe 1. +Lösung Entscheiden Sie, welcher der folgenden Wörter w1 , . . . , w5 über dem Alphabet Σ ta, b, c, du Elemente der Sprachen L1 , . . . , L5 sind: L1 L2 L3 L4 L5 ta, bu ta, butcutdu tanbn | n P Nu L1L2 L2 Y tabbau w1 abcd nein nein nein ja nein w2 abba ja nein nein nein ja w3 cba nein nein nein nein nein w4 aabbccdd w5 nein nein nein nein nein Aufgabe 2. Zeigen Sie, daß die Sprachen L1 tw P t0, 1u | w enthält eine ungerade Anzahl von 1enu L2 tw P t0, 1u | 111000 ist ein Anfangswort von wu L3 tw P t0, 1u | w enthält nicht 001 als Teilwortu regulär sind, indem Sie für i 1, 2, 3 reguläre Ausdrücke αi mit Lpαi q Li angeben. Lösung Lpp010qp0|101qq L2 Lp111000p0|1q q L3 Lpp1|01q 0 q L1 1 cddd nein nein nein nein nein Aufgabe 3. Wir bezeichnen zwei reguläre Ausdrücke α und β über einem Alphabet Σ als äquivalent – in Zeichen α β – wenn α β ðñ Lpαq Lpβ q. D.h. zwei reguläre Ausdrücke sind genau dann äquivalent wenn sie die gleichen Sprachen erzeugen. Beweisen Sie die folgenden Formeln für beliebige reguläre Ausdrücke α, β, γ: (a) α|α α (b) α|β (c) β |α α pα q Lösung (a) Weil Lpα|αq Lpαq Y Lpαq Lpαq. (b) Lpα|β q Lpαq Y Lpβ q Lpβ q Y Lpαq Lpβ |αq (c) Lppαq q Lpαq pLpαq q Lppαq q Lppα q q. Da für eine beliebige Sprache L gilt, daß pLq L; offensichtlich ist L pLq. Um zu sehen, daß auch die umgekehrte Inklusion gilt, sei w P pL q . D.h. es gibt Wörter v1 , . . . vn P L , so daß w v1 . . . vn . Für jedes dieser Wörter gibt es aber jeweils Wörter ui,1 , . . . , ui,mi P L so daß vi ui,1 . . . ui,mi . Insgesamt ist also w u1,1 u1,2 . . . u1,m1 u2,1 . . . un,mn , und also w P L . Aufgabe 4. Sei Σ ta, b, c, du und L die Sprache tw P Σ | es gibt ein Symbol in Σ, das nicht in w enthalten istu. Konstruieren Sie einen ε-NDEA, der L akzeptiert. Beschreiben Sie die Idee bzw. die Arbeitsweise Ihres Automaten. Lösung / @ABC GFED q0 PP AA PP } AA PPP } } ε } AAε PPεP } ε PPP AA }} PPP A } }~ ' ?>=< @ABC GFED 89:; ?>=< @ABC GFED 89:; ?>=< @ABC GFED 89:; ?>=< @ABC GFED 89:; q1 q2 q3 q4 I I I I start b,c,d a,c,d a,b,d a,b,c Die Idee hinter der Arbeitsweise dieses Automaten ist, daß der Automat (nichtdeterministisch) rät“ ob ” ein eingegebenes Wort kein a, b, c oder d enthält und mit einem ε-Übergang in einen entsprechenden Zustand wechselt. ENDE 2











