- Edu

Vokabelliste
FB Mathematik
Vokabeln 7./8. Klasse // Vokabeln 9./10. Klasse // Vokabeln Sek II
Mathematik
Symbol, Definition
Deutsch
Erklärung
Beispiel/ weitere Hinweise
Mengenbegriffe:
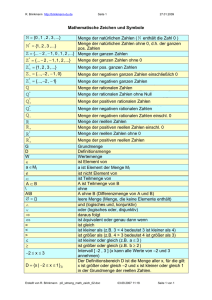
ℕ
ℕ0
ℤ
ℚ
ℤ+
ℚ+
0
𝐴 = {𝑎1 , … , 𝑎𝑛 }
{}
𝑥∈ℚ
∉
𝐴⊂𝐵
bezeichnet die Menge der
natürlichen Zahlen
bezeichnet die Menge der
natürlichen Zahlen inkl. der 0
bezeichnet die Menge der
ganzen Zahlen
bezeichnet die Menge der
rationalen Zahlen (Brüche)
bezeichnet die Menge der
positiven ganzen Zahlen
Bezeichnet die Menge der
positiven rationalen Zahlen
inkl. der Null
Bezeichnet die Menge A.
Zwischen geschweiften
Klammern stehen Elemente die
zusammen eine Menge bilden,
hier: 𝑎1 , … , 𝑎𝑛 .
1; 2; 3; 4; …
0; 1; 2; 3; 4; …
…; -3; -2; -1; 0; 1; 2; 3;…
1 5 3
; ; ;
2 10 3
2; 1,25; 1,333; …
1; 2; 3; 4; …
Klar.
𝑃 = {2,3,5,7, … }ergibt
fortgesetzt die Menge der
Primzahlen
Leere Menge
… also eine Menge in der
einfach nichts drin ist.
heißt, dass die Werte x aus den
rationalen Zahlen stammen.
Man spricht x Element Q.
x kann also jede rationale Zahl
sein
nicht Element von
A ist Teilmenge von B
∪
Vereinigung (oder)
∩
Schnittmenge (und)
1
Hier werden Werte für x
ausgeschlossen 𝑥 ∉ ℤ+ heißt,
dass x keine positive ganze Zahl
ist
ℕ ⊂ ℤ, weil alle natürlichen
Zahlen in den ganzen Zahlen
enthalten sind. Es gilt übrigens
ℕ⊂ℤ⊂ℚ⊂ℝ
𝐴 ∪ 𝐵 heißt, nimm alle
Elemente die in A oder B sind
𝐴 = {1; 2; 3; 4}
𝐵 = {3; 4; 5; 6}
dann ist
𝐴 ∪ 𝐵 = {1; 2; 3; 4; 5; 6}
𝐴 ∩ 𝐵 heißt, nimm alle
Elemente die in A und B sind
𝐴 = {1; 2; 3; 4}
𝐵 = {3; 4; 5; 6}
dann ist 𝐴 ∩ 𝐵 = {3; 4}
Vokabelliste
FB Mathematik
ℝ\ℕ bezeichnet die Menge der
reellen Zahlen ohne die Menge
der natürlichen Zahlen
ℚ \{0} bezeichnet die Menge
der rationalen Zahlen ohne die
Null
ℝ\{𝑎, 𝑏, 𝑐}
bezeichnet die Menge der
reellen Zahlen ohne die
Elemente a, b und c
𝑛≤𝑖≤𝑚
i liegt zwischen n und m, der
Buchstabe in der Mitte
bezeichnet meist eine Variable
oder einen (Lauf-)Index, im
Bereich von n bis m
0≤𝑖≤∞
i liegt zwischen Null und
Unendlich
bezeichnet die Menge der
reellen Zahlen
ℚ zzgl. alle nicht abbrechenden
und nicht periodischen
Dezimalzahlen, wie
1,12345678911223344…
√2; 𝜋; Φ;…
ℝ
ℝ−
ℝ+
𝐴𝑎 mit 𝑎 ∈ {1,2,3 … }
bezeichnet die Menge der
negativen reellen Zahlen
bezeichnet die Menge der
positiven reellen Zahlen
Indexschreibweise von
ähnlichen, hier unendlich vielen
durchnummerierten Elementen
Klar.
Klar.
Kann man gut für Kurvenschare
nehmen
𝑓𝑎 (𝑥) = 𝑥 2 + 𝑎 mit 𝑎 ∈ ℝ
meint alle nach unten und oben
verschobenen Normalparabeln
Relationen:
𝑎>𝑏
a ist echt größer als b
𝑎≫𝑏
a ist viel größer als b
𝑎≥𝑏
a ist größer als b oder gleich b
𝑎<𝑏
a ist echt kleiner als b
𝑎≪𝑏
a ist viel kleiner als b
𝑎≤𝑏
a ist kleiner als b oder gleich b
𝑎≈𝑏
a ist ungefähr so groß wie b
a ist gerundet b
|𝑎|
Betrag von a (Vorzeichen egal)
2
Echt heißt nicht gleich groß!
Man merke, da wo der Pfeil
auseinander ist, ist‘s größer.
Wenn 𝑎 ≫ 1 dann könnte a für
1.000 oder 1.000.000 stehen
Klar.
Da wo der Pfeil spitz ist, ist’s
kleiner.
Echt heißt nicht gleich groß!
Man merke, da wo der Pfeil
auseinander ist, ist‘s größer.
Klar.
𝜋 ≈ 3,14
|−2| = 2
Vokabelliste
FB Mathematik
Bezeichnungen und gängige Symbolik:
x und y
A,B,C,…
P, Q
̅ 𝐴,
̃ 𝐴̂, A‘, A‘‘
𝐴,
𝛼, 𝛽, 𝛾, 𝛿, 𝜀, …
𝜋
𝜇, 𝜆
Meist als unabhängige Variable
und Kurzbezeichnung für f(x)
genutzt und
Punktebezeichnung in
Reihenfolge (mathematischer
Drehsinn = entgegen des
Uhrzeigersinn) für
geometrische Figuren
Beliebige Punkte
Hat meist irgendwas mit A zu
tun;
𝐴̅ bezeichnet manchmal das
Gegenteil von A
Griechische Buchstaben
werden gerne für Winkel
genutzt…
außer das Pi! Das steht in der
Regel für Pi= 𝜋 ≈3,14
Naja und die beiden
(ausgesprochen Lambda und
Mü) stehen meist als
Stellvertreter für sehr kleine
Zahlen
Klar.
Dreieck beschriften
Zwecks Übersichtlichkeit
hilfreich ist manchmal den
Koordinaten gleiche
Kleinbuchstaben zu geben
𝑃(𝑝1 |𝑝2 ) 𝑢𝑛𝑑 𝑄(𝑞1 |𝑞2 )
Spiegelpunkte, Schnittpunkte,
parallele Geraden 𝑓̃,…
𝛼 = 90°
Sonderzeichen:
≠
Ungleich (was im Endeffekt das
Gegenteil von = ist)
∅
Durchschnitt
⋕
Anzahl
∞
Unendlich
𝑥 ≠ 0, in der Regel gilt hier: x
darf alles sein außer Null
(praktisch wenn x ein Nenner
2
ist: denn da darf man ja nicht
𝑥
durch Null teilen ;)
Gerne für Klassenarbeiten
verwendet  Es handelt sich
hier lediglich um das
arithmetische Mittel.
Sei 𝑀 = {2; 3; 5; 7; 11} dann
besteht M aus 5 Elementen.
#𝑀 = 5
Klar.
3
Vokabelliste
FB Mathematik
In der p-q-Formel spielt diese
Abkürzung ihre Stärke aus.
Statt zwei Formeln zu schreiben
±
Plus Minus, kann genutzt
werden um zwei Ergebnisse
oder Rechnungen in eine
Gleichung zu schreiben
𝑝
𝑝2
𝑥1 = − + √ − 𝑞
2
4
𝑝
𝑝2
𝑥2 = − − √ − 𝑞
2
4
kann man auch nur…
𝑝
𝑝2
𝑥1,2 = − ± √ − 𝑞
2
4
schreiben.
!
Fakultät (Multiplikation aller
natürlichen Zahlen bis …)
4! = 1 ∙ 2 ∙ 3 ∙ 4
√𝑥
Wurzel von x
√4 = 2
3
Dritte Wurzel von x
3
√𝑥
√8 = 2
Gerne verwendet für lange
unmerkbare Zahlen… Sind
deine Nullstellen aus Versehen
0,124567891234678 und
-0,124567891234678 dann
kann es Sinn machen, diese
Zahl abzukürzen, falls sie noch
oft gebraucht und geschrieben
wird
𝑛1 := 0,124567891234678
𝑛2 ≔-0,124567891234678
∃ 𝑥 ∈ ℝ: 𝑓(𝑥) = 0
Übersetzung: Es gibt ein x aus
den reellen Zahlen für das die
Funktion f eine Nullstelle hat.
∀ 𝑥 ∈ ℝ: 𝑓(𝑥) > 0
Übersetzung: Für alle x, die du
aus den reellen Zahlen einsetzt:
Die Funktion f liegt immer über
der x-Achse.
∶=
Wird definiert als…
∃
Abk. für: Es gibt…
∀
Abk. für: Für alle…
∧
Abk. für und
Du und ich = Du ∧ Ich
∨
Abk. für oder
Du oder ich = Du ∨ Ich
¬
Abk. für nicht
nicht gegeben = ¬gegeben
4
Vokabelliste
FB Mathematik
Geometrie:
∢𝐴𝐵𝐶
Winkel bei B
⊿𝐴𝐵𝐶
Bezeichnet das Dreieck ABC
Bezeichnung der Buchstaben
im mathematischen Drehsinn
(entgegen des Uhrzeigersinn)
Bezeichnung der Buchstaben
im mathematischen Drehsinn
(entgegen des Uhrzeigersinn)
Bezeichnet einen Punkt P mit
den Koordinaten x und y
𝑃(𝑥|𝑦)
̅̅̅̅
𝐴𝐵
̅̅̅̅|
|𝐴𝐵
(gängige Trennungen zwischen den
Koordinaten sind | und ; nur nicht , weil
man bei , nicht unterscheiden kann, ob bei
1,2 die Zahl 1,2 oder die Koordinaten 1 und
2 gemeint sind)
Bezeichnet eine Strecke von A
nach B
Bezeichnet die Länge der
Strecke von A nach B
∥
parallel
∦
Nicht parallel
⊥
senkrecht
⊿𝐴𝐵𝐶 ≅ ⊿𝑃𝑄𝑅
⃗⃗⃗⃗⃗
𝐴𝐵
𝑣
⃗⃗⃗⃗⃗ |
|𝐴𝐵
Die Dreiecke ABC und PQR sind
kongruent.
Vektor von A nach B
Vektor / Gerade v
Klar.
Klar.
̅̅̅̅| = 4𝑐𝑚
|𝐴𝐵
𝑔 ∥ ℎ, dann sind die Geraden g
und h parallel.
𝑔 ∦ ℎ, dann sind die Geraden g
und h nicht parallel.
𝑔 ⊥ ℎ, dann sind die Geraden g
und h parallel.
Kann man auch für andere
Figuren verwenden!
1
⃗⃗⃗⃗⃗
𝐴𝐵 = ( )
2
1
1
𝑣 = ( )𝑥 + ( )
2
2
Länge des Vektors v
Intervalle:
(𝑎, 𝑏)
Von a bis b, ohne a und b
Klar.
[𝑎, 𝑏]
Von a bis b, inklusive a und b
Klar.
(𝑎, 𝑏]
[𝑎, 𝑏)
Von a bis b, ohne a und
inklusive b
Von a bis b, inklusive a und
ohne b
5
Klar.
Klar.
Vokabelliste
FB Mathematik
Pfeile:
Es hat geregnet. ⟹ Die Straße
ist nass.
Die Straße ist nass. ⇏ Es hat
geregnet. (Könnte ja auch ein
Rohrbruch Schuld sein…)
⇒
Aus links folgt rechts
⇏
Aus links folgt nicht rechts
⇐
Aus rechts folgt links
p ist ungerade ⇐ p ist Primzahl
⇍
Aus rechts folgt nicht links
p ist Primzahl ⇍ p ist ungerade
⇔
Links folgt rechts und rechts
folgt links (äquivalent)
Dreieck A und B sind kongruent
⇔ Dreieck A und B haben
jeweils drei gleich lange Seiten
(sss)
⇎
Nicht äquivalent
Klar.
⟶
Geht nach (für Grenzwerte);
Nähert sich an
oder
(𝐴 ⟶ 𝐵)
Pfeil für Abbildung:
Menge A geht auf Menge B
↗
↘
𝑥 ⟼ 𝑓(𝑥)
Nähert sich von unten an
Nähert sich von oben an
Pfeil für Abbildung:
Element x aus Menge A geht
auf Element der Menge B mit
folgender Zuordnungsvorschrift
f(x)
6
𝑎 → ∞ dann strebt a nach
Unendlich
𝑓: ℝ ⟶ ℝ dann beschreibt die
Funktion f eine Abbildung von
den reellen Zahlen in die
reellen Zahlen ...*
𝑎 → −1 dann strebt a nach
Minus 1 und man betrachte
bspw. den Graphen von links
kommend
𝑎 → 𝜋 dann strebt a nach Pi
und man betrachte bspw. den
Graphen von rechts kommend
* … also in vollständig wird eine
Abbildung dann so definiert:
𝑓: ℝ ⟶ ℝ
𝑥 ⟼ 𝑥2 + 𝑥
Vokabelliste
FB Mathematik
Schreibweisen:
100
∑ 𝑥𝑖
𝑚
∑ 𝑥𝑖 𝑚𝑖𝑡 𝑛 ≤ 𝑖 ≤ 𝑚
𝑛
𝑚
∏ 𝑥𝑖 𝑚𝑖𝑡 𝑛 ≤ 𝑖 ≤ 𝑚
𝑛
𝑙𝑖𝑚 𝑓(𝑥)
𝑥⟶∞
𝑚𝑖𝑛(𝑎, 𝑏, 𝑐 … )
𝑚𝑎𝑥(𝑎, 𝑏, 𝑐 … )
Summe der Elemente 𝑥𝑖 von n
bis m
Produkt der Elemente 𝑥𝑖 von n
bis m
Grenzwert der Funktion f(x)
wenn x nach unendlich strebt
Das Minimum der Werte a, b,
c…
Das Maximum der Werte a, b,
c…
Integralrechnung:
∫ 𝑓(𝑥)𝑑𝑥
𝑎
∫ 𝑓(𝑦)𝑑𝑦
𝑏
Meint das unbestimmte
Integral von der Funktion f;
dx sagt aus, dass die Variable x
ist
Meint das bestimmte Integral
von der Funktion f im Intervall
von a bis b; die Variable ist hier
y
7
𝑛=0
mit 𝑥𝑖 ∈ ℕ heißt im Klartext:
Addiere die natürlichen Zahlen
auf – und zwar nicht alle,
sondern nur bis 100.
Wie eben nur mit Mal nehmen.
1
=0
𝑥⟶∞ 𝑥
𝑙𝑖𝑚
𝑚𝑖𝑛(ℕ) = 1
𝑚𝑎𝑥(ℚ−
0) = 0