Musterlösung Blatt 6

13. September 2017
Elektrizitätslehre I
Martin Loeser
Musterlösung Blatt 6
1/2
EL1, Übung 4
1
Aufgabe 1
Potentiometer
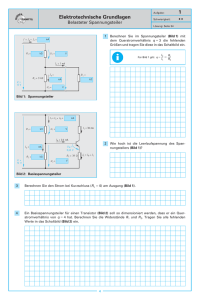
a) Bestimmen Sie die Spannungsquellenersatzschaltung der
unbelasteten Potentiometerschaltung und
geben sie deren Parameter Uqe und Rie in Funktion der normierten Schleiferstellung x formal und in
einer normierten Graphik an.
I
x
Rp
Uq
U
Last
b) Skizzieren Sie die U-I-Kennlinienschar der Schaltung für die normierten Schleiferstellungswerten
x = 0.25 / 0.5 / 0.75 / 1 als Parameter. Bei welchem x-Wert ist die Kennlinie am steilsten?
Abbildung
1: Potentiometer
c) Skizzieren Sie die Verläufe
der Ausgangsspannung
in Funktion der normierten Schleiferstellung x,
falls die Schaltung mit den Lastwiderständen RL= 10·Rp, Rp und Rp/10 belastet wird.
Die Ersatzquelle
durch
Leerlaufspannung
und Kurzschlussstrom.
Hinweis wird
zu dendefiniert
graphischen
Darstellungen:
Um allgemeingültige
Graphiken zu erhalten,
Spannung
U
mit
U
und
die
Stromstärke
I
mit
U
/R
normiert
dargestellt
werden.
q
q
p
Leerlaufspannung:
Aufgabe 2
(1 − x) Rp
Uq = (1 − x)U
0 = die Spannungsquellenersatzschaltung
a) Bestimmen USie
derq folgenden
Brückenschaltung. x Rp + (1 − x)Rp
Kurzschlussstrom:
R1
Ik =
Uq
Ri =
U0R2
Ik
spannungsgespeisten
Uq R3
x Rp
I
Innenwiderstand
kann die
U
R4
= x(1 − x) Rp
Die Kennlinien
sind
in der
folgenden
Abbildung
dargestellt.
b) Unter
welcher
allgemeinen
Bedingung
verschwindet
deren Leerlaufspannung (Uq ≠ 0)?
c) Wie verhält
sich die
Leerlaufspannung
U = U0man
in Funktion
von ∆R, wenn einfach
für die Widerstände
gilt: R1
Für den letzten
Teil der
Aufgabe
betrachtet
die Schaltung
als Span= R4 = R und R2 = R3 = R + ∆R?
nungsteiler:
d) An den Klemmen der Schaltung wird der
R0 angeschlossen. Bestimmen Sie formal
RBrückenwiderstand
L
die Stromstärke in diesem Widerstand.
U=
U0
Ri + RL
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
4. Dezember 2003, © M. Schlup
Musterlösung Blatt 6, Elektrizitätslehre I
2
10
U = 10V
q
8
U0 [V]
6
4
2
0
0
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1
25
Rp = 100 Ω
20
Ri [Ω]
15
10
5
0
0
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1
Abbildung 2: Leerlaufspannung und Innenwiderstand.
Mit den Ergebnissen aus der ersten Teilaufgabe gilt dann
U=
RL
(1 − x) Uq
x(1 − x)Rp +RL | {z }
{z
|
=Ri
=U0
}
Dann ergibt sich
RL =
2
Rp
:
10
U=
1−x
Uq
10x(1 − x) + 1
RL = Rp :
U=
1−x
Uq
x(1 − x) + 1
RL = 10Rp :
U=
10(1 − x)
Uq
x(1 − x) + 10
Brückenschaltung
Für das Ersatzschaltbild benötigen wir Leerlaufspannung und Innenwiderstand –
das Vorgehen haben wir in der Vorlesung schon behandelt.
Leerlaufspannung (zweimal der Spannungsteiler)
U0 =
R2
R4
−
R1 + R2 R3 + R4
Uq
1/2
EL1, Übung 4
Aufgabe 1
Musterlösung Blatt 6, Elektrizitätslehre I
3
a) Bestimmen Sie die Spannungsquellenersatzschaltung der unbelasteten Potentiometerschaltung und
geben sie deren Parameter Uqe und Rie in Funktion der normierten Schleiferstellung x formal und in
10
einer normierten
Graphik an.
R =R /10
L
p
RL=Rp
RL = 10 Rp
9
8
UL
6
I
x
Rp
7
Uq
U
Last
5
4
b) Skizzieren Sie die U-I-Kennlinienschar der Schaltung für die normierten Schleiferstellungswerten
x = 0.25
/ 0.5 / 0.75 / 1 als Parameter. Bei welchem x-Wert ist die Kennlinie am steilsten?
3
c) Skizzieren
Sie die Verläufe der Ausgangsspannung in Funktion der normierten Schleiferstellung x,
2
falls die Schaltung mit den Lastwiderständen RL= 10·Rp, Rp und Rp/10 belastet wird.
1
Hinweis zu den graphischen Darstellungen: Um allgemeingültige Graphiken zu erhalten, kann die
Spannung 0U
mit 0.1
Uq und0.2die Stromstärke
I 0.5mit Uq0.6/Rp normiert
dargestellt
werden.
0
0.3
0.4
0.7
0.8
0.9
1
x
Aufgabe 2
Abbildung 3:Sie
Ausgangsspannungen
als Funktion der Schleiferstellung.
a) Bestimmen
die Spannungsquellenersatzschaltung
der folgenden
Brückenschaltung.
R1
Uq
spannungsgespeisten
R3
I
U
R2
R4
b) Unter welcher allgemeinen Bedingung verschwindet deren Leerlaufspannung (Uq ≠ 0)?
Abbildung 4: Brückenschaltung
c) Wie verhält sich die Leerlaufspannung U = U0 in Funktion von ∆R, wenn für die Widerstände gilt: R1
= R4 = R und R2 = R3 = R + ∆R?
Sie verschwindet genau dann, wenn gilt
d) An den Klemmen der Schaltung wird der Brückenwiderstand R0 angeschlossen. Bestimmen Sie formal
R1
R3
die Stromstärke in diesem Widerstand.
=
U0 = 0 ⇔
R2
R4
Für den Innenwiderstand findet man (siehe Vorlesung)
Ri = (R1 ||R2 ) + (R3 ||R4 ),
wobei wie üblich gilt
Ra Rb
.
Ra + Rb
Mit R1 = R4 = R und R2 = R3 = R + ∆R gilt
Ra ||Rb =
——————————————————————————————————————————————————
R + ∆R
R
∆R
U0 =
−
Uq =
Uq . 4. Dezember 2003, © M. Schlup
Zürcher Hochschule
Winterthur, Departement
T
R + R + ∆R
R + R + ∆R
2R + ∆R
Musterlösung Blatt 6, Elektrizitätslehre I
4
Für kleine Verstimmungen ∆R R gilt dann
U0 ≈
∆R
,
2R
die Leerlaufspannung wächst also linear mit der Verstimmung.
Der Stromfluss ergibt sich zu
U0
I=
Ri + R0
Im Falle der schwach verstimmten Brücke findet man Ri ≈ R
3
EL1, Übung 4, Lösungen
Ersatzquelle
2/3
Aufgabe 3
a)
I
R1
I
R3
R1
R2+R 3
U
Uq1
U
Uq2 =
R2 Iq2
Uq1
R2
Iq2
Iqe =Iq1 – Iq3 =
Uq1/R1 –
Iq2·R2/(R2+R 3)
I
Iq1 =
Uq1/R1
R2+R 3
R1
I
Rie =
R1//(R2+R 3)
U
U
Iq3 =
Uq2/(R2+R 3)
I qe =
Uq1
U (R + R 3 ) " R1 R 2 Iq 2
R2
R (R + R 3 )
, R ie = 1 2
,
"
I = q1 2
R1 R 2 + R 3 q 2
R1 (R 2 + R 3 )
R1 + R 2 + R 3
Abbildung 5: Quellenwandlung nach Norton.
U (R + R 3 ) " R1 R 2 Iq 2
U qe = R ie I qe = q 1 2
R1 + R 2 + R 3
(a) Bestimmen Sie die Quellenersatzgrössen bezüglich der Klemmen nach Thevenin
R (R + R )
R +R
R R
und Norton
der folgenden
Schaltung
durchI Quellentransformation.
b) Leerlaufspannung:
U =
U +
"
I
2
0
3
2
q1
R1 + R2 + R3
2
3
R1 + R2 + R3
q2
1
3
R1 + R2 + R3
q2
(b) Bestimmen Sie mit Hilfe des
Superpositionsprinzips
die Leerlaufspannung U0
U
R
Kurzschlussstromstärke: I =
"
I
R . R +R
und den Kurzschlusstrom
I
C
!
q1
2
C
q2
1
2
3
R1 (R 2 + R 3 )
c) R = RSie
//(R den
+ R ) Innenwiderstand
=
(c) Bestimmen
der Schaltung direkt durch Nullsetzen der
R +R +R
Quellen
und vergleichen Sie das Ergebnis mit dem Verhältnis U0/Ic .
Aufgabe 4
ie
1
2
3
1
2
R
Ersatzschaltung
nach Norton:
a) Leerlaufspannung:
U =
0
3
2
R1 + R 2
U q1 +
R 2 Uq 1 + R1 R 2 I q 2
R1 R 2
I =
= 12 V
R1 + R 2 q 2
R1 + R 2
Uq1
R2
I0Uq1=+ I q 2 = 250−mA
Iq2 ,
Kurzschlussstromstärke: I C =
R1
R1
R2 + R3
b) R ie = R1 //R 2 =
!
R1 R 2
= 48 "
R1 + R 2
Ri =
R1 (R2 + R3 )
,
R1 + R2 + R3
——————————————————————————————————————————————————
3
q1
1 7. November
2 q2
Zürcher Hochschule Winterthur, Departement T 2
2007, © M. Schlup
U0 = Ri I0 =
(R + R ) U − R R I
R1 + R2 + R3
Musterlösung Blatt 6, Elektrizitätslehre I
5
Anwendung des Superpositionsprinzips
U0 =
R2 R3
R2 (R1 + R3 )
R2 + R3
Uq1 +
Iq2 −
Iq2 ,
R1 + R2 + R3
R1 + R2 + R3
R1 + R2 + R3
I0 =
R2
Uq1
−
Iq2 .
R1
R2 + R3
Innenwiderstand:
Ri = R1 ||(R2 + R3 ) =
R1 (R2 + R3 )
R1 + R2 + R3