WS14_Vorlesung_5_Kapaz_Strom_Widerstand copy

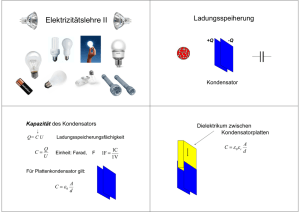
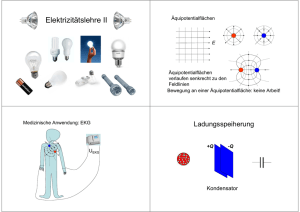
WS/2014
Vertiefung Experimentalphysik 1 (LB-Technik)"
E. Resconi
Kapazität (Kapitel 26)
Plattenkondensator
ΔV = E ・d
U = 1/2 Q・V
Kapazität des Kondensator
C = Q/ V
[C]= Coulomb/Volt = Farad
C = Q/V = A
ε0 / d
Die Größe der Kapazität ist durch ausschließlich die Geometrie des
Plattensystems abhängig. Die Kapazität ist ein Maß dafür wie viel Ladung auf
den Kondensator gebracht werden muss um eine bestimmte
Potenzialdifferenz zwischen seinen Platten zu erzeugen (Analogie Gummi die
wird gestressed).
Die Distanz d muss sehr klein sein: chemische Reaktion.
Der Kondensator ist ein passives elektrisches Bauelement mit der Fähigkeit
elektrische Ladung und damit zusammenhängend Energie zu speichern.
(Zylinderkondensator, Kugelkondensator ==> Übungen, Seite 550 in Buch)
Parallelschaltungen und Reihenschaltungen von Kondensatoren
n Kondensatoren sind parallelgeschaltet ==> alle positiv (negative)
geladenen Platten sind miteinander verbunden und liegen somit auf
demselben Potential. Der Potentialabfall ist demnach an jedem Kondensator
derselbe:
U1 = U 2 = U
Die Gesamtladung ist gleich der Summe der Ladungen auf jedem einzelnen
Kondensator:
Q1 + Q2 = Q
C1 U + C2 U = Ctot U
Parallel: Ctot = q/V = C1+C2+C3+...
1
WS/2014
Vertiefung Experimentalphysik 1 (LB-Technik)"
E. Resconi
Kondensatoren in Reihe: die Ladung auf jedem Kondensator ist dieselbe
Q1 = Q2 = Q
Der gesamte Potentialdifferenz an der Schaltung ist die Summe der
Potentialdifferenzen an jedem einzelnen der Kondensatoren. Die
Potentialdifferenz ist
U1 + U2 = U
und U = Q / C ==> Q / C1 + Q / C2 = Q / Ctot
wobei
Ctot = Q / U
Reihen: 1/Ctot = 1/C1 + 1/C2 + 1/C3 + ...
2
WS/2014
Vertiefung Experimentalphysik 1 (LB-Technik)"
E. Resconi
Elektrischer Strom und Widerstand (Kapitel 27)
Strom = Ladungen in Bewegung in eine Richtung
Nicht jede Ladung in Bewegung ist automatisch Strom: nur wenn effektiv eine
Ladungstransport durch eine Fläche hindurch stattfindet. [4]
Beispiel: In einem isolierten Kupferdraht, Raum Temperatur (300K) [2]: die
freien Elektronen bewegen sich sehr schnell
<ve> = 106 m/s
aber ungeordnet => keinen Ladungstransport ! Keine Strom !
Kollisionszeit = 3 ・ 10-14 sec = τ
n = 1029 = Zahl von frei Elektronen in Kupfer / m3
Wir legen eine Potentialdifferenz an der Kupferdraht => die Elektronen
erfahren eine Kraft
F=eE
Sie werden beschleunigt
a = F / me = e E / me(me = Masse von Elektron)
sie bewegen sie sich mit einer Geschwindigkeit
vd = a ・ τ = e E / me ・ τ = Drift-geschwindigkeit
if E ⇑ vd
⇑ ... intuitive.
Beispiel:
Kupfer = 10 m, ΔV = 10 Volts, E im Kupfer = 1 V / m
vd = 5 10-3 m/s
Die Elektronen brauchen 1/2 Stunden für die Bewegung in Kupfer. Nicht
intuitive!
3
WS/2014
Vertiefung Experimentalphysik 1 (LB-Technik)"
Ohmsches Gesetz
L = Length
E=V/L
(27-6 Ohmshce Gesetz mikroskopisch betrachtet)
Wie viele Elektronen in Querschnitt
I = vd ・ A ・ n ・e = (n = No. Elektronen, e = Ladung Elektronen)
= e E / me ・ τ ・ A ・ n ・ e =
= e2 n τ / m e ・ A ・ E
σ = e2 n τ / me = Leitfähigkeit (conductivity)
ϱ = 1/σ = spezifisch Widerstand
4
E. Resconi
WS/2014
Vertiefung Experimentalphysik 1 (LB-Technik)"
E. Resconi
aber E = V/L
I = σ A V / L oder
V = L/ σ A ・ I
R = L / σ A = Widerstand
[R] = Ohm = Volt / Amper = Ω
V=R・I#
Ohm Gesetz
Ein Leiter erfüll dem ohmschen Gesetz wenn ein durch ihn fließender Strom
immer direkt proportional der angelegten Potenzialdifferenz ist.
Tatsächlich gilt das Gesetz nur in engem Rahmen und nur für einige Stoffe. Das ist
die Basis für das Verständnis der Zusammenhänge zwischen Stromstärke und
Spannung in elektrischen Stromkreisen.
5