Vorlesung Trigonometrie
Werbung
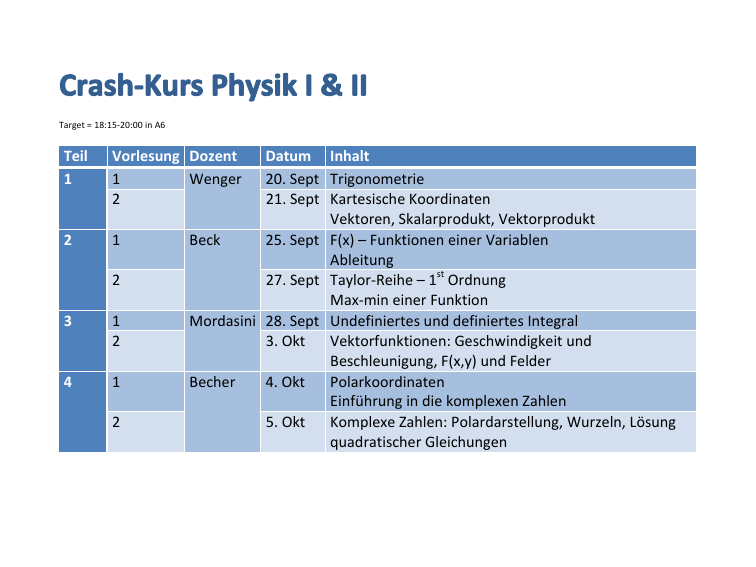
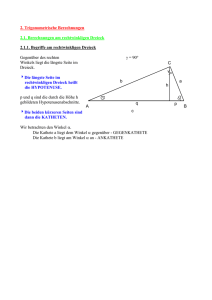
Target = 18:15-­‐20:00 in A6 Teil 1 Vorlesung Dozent 1 Wenger 2 2 1 2 3 1 2 4 1 2 Datum Inhalt 20. Sept Trigonometrie 21. Sept Kartesische Koordinaten Vektoren, Skalarprodukt, Vektorprodukt Beck 25. Sept F(x) – Funktionen einer Variablen Ableitung 27. Sept Taylor-­‐Reihe – 1st Ordnung Max-­‐min einer Funktion Mordasini 28. Sept Undefiniertes und definiertes Integral 3. Okt Vektorfunktionen: Geschwindigkeit und Beschleunigung, F(x,y) und Felder Becher 4. Okt Polarkoordinaten Einführung in die komplexen Zahlen 5. Okt Komplexe Zahlen: Polardarstellung, Wurzeln, Lösung quadratischer Gleichungen Crash Course in Mathematik für Physik I und II Urs Wenger Albert Einstein Center für fundamental Physik Universität Bern Teil 1, Vorlesung 1: Trigonometrie Trigonometrie – Lernziele von heute: I Kenntnis der Begriffe: I I I Fähigkeit in rechtwinkligen Dreiecken: I I I zu jeder Winkelfunktion ein Seitenverhältnis anzugeben fehlende Seitenlängen und Winkel zu berechnen Fähigkeit in beliebigen Vielecken: I I Gegenkathete, Ankathete, Hypotenuse Grad- und Bogenmass fehlende Seitenlängen und Winkel zu berechnen Fähigkeit zwischen Grad- und Bogenmass umzurechnen Was ist Trigonometrie? Begriff der Trigonometrie: Tri ⇐⇒ drei Gon ⇐⇒ Winkel, Ecke Metrie ⇐⇒ Messung Triathlon, . . . Pentagon (5 − Eck), . . . Geometrie (Erdvermessung ), . . . Was ist Trigonometrie? Begriff der Trigonometrie: Tri ⇐⇒ drei Gon ⇐⇒ Winkel, Ecke Metrie ⇐⇒ Messung Triathlon, . . . Pentagon (5 − Eck), . . . Geometrie (Erdvermessung ), . . . Trigonometrie Dreiwinkelmessung, Dreiecksberechnung Begriffe im rechtwinkligen Dreieck I Hypotenuse: I Seite, welche dem rechten Winkel gegenüberliegt (längste Seite gegenüber dem grössten Winkel) Katheten Seiten, welche den rechten Winkel bilden · Kathete Kathete Hypotenuse Begriffe im rechtwinkligen Dreieck I Hypotenuse: I I Seite, welche dem rechten Winkel gegenüberliegt (längste Seite gegenüber dem grössten Winkel) Katheten: I Seiten, welche den rechten Winkel bilden · Kathete Kathete Hypotenuse Begriffe im rechtwinkligen Dreieck I Ankathete: I einem Winkel anliegende Kathete Gegenkathete von α · Ankathete von α Hypotenuse α Begriffe im rechtwinkligen Dreieck I Ankathete: I I einem Winkel anliegende Kathete Gegenkathete: I einem Winkel gegenüberliegende Kathete Gegenkathete von α · Ankathete von α Hypotenuse α Begriffe im rechtwinkligen Dreieck I Je nach Lage des Winkels ändert sich die Lage der Gegen- und Ankathete: α · Begriffe im rechtwinkligen Dreieck I Je nach Lage des Winkels ändert sich die Lage der Gegen- und Ankathete: α · Beispiel 1: Gegenkathete von α Begriffe im rechtwinkligen Dreieck I Je nach Lage des Winkels ändert sich die Lage der Gegen- und Ankathete: α · Beispiel 1: Gegenkathete von α Ankathete von α Begriffe im rechtwinkligen Dreieck I Je nach Lage des Winkels ändert sich die Lage der Gegen- und Ankathete: α · β Beispiel 1: Gegenkathete von α Ankathete von α Beispiel 2: Ankathete von β Gegenkathete von β Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC B c a A · α C1 C Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 a a1 A α · C1 · C Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 B2 c2 A α a a1 a2 · C2 · C1 · C Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 B2 c2 A I α a a1 a2 · C2 · C1 · C Dreiecke ABC , AB1 C1 , AB2 C2 sind ähnlich zueinander Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 B2 c2 A I I α a a1 a2 · C2 · C1 · C Dreiecke ABC , AB1 C1 , AB2 C2 sind ähnlich zueinander Gemäss Strahlensatz gilt a1 a2 a = = = . . . = durch α bestimmt c c1 c2 Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 B2 c2 A I I α a a1 a2 · C2 · C1 · C Dreiecke ABC , AB1 C1 , AB2 C2 sind ähnlich zueinander Gemäss Strahlensatz gilt a1 a2 a = = = . . . = durch α bestimmt c c1 c2 Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 B2 c2 A I I α a a1 a2 · C2 · C1 · C Dreiecke ABC , AB1 C1 , AB2 C2 sind ähnlich zueinander Gemäss Strahlensatz gilt a1 a2 a = = = . . . = trigonometrische Fkt. von α c c1 c2 Definition einer Winkelfunktion I Gegeben sei ein rechtwinkliges Dreieck ABC mit Parallele B1 C1 , B2 C2 zur Kathete a: B B1 c c1 B2 c2 A I I α a a1 a2 · C2 · C1 · C Dreiecke ABC , AB1 C1 , AB2 C2 sind ähnlich zueinander Gemäss Strahlensatz gilt a1 a2 a = = = . . . ≡ sin α c c1 c2 (Sinus von α) Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A · Ankathete b C Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A · α Ankathete b C Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A · α Ankathete b C Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A I · α Ankathete b C Alle rechtwinkligen Dreiecke mit demselben Winkel α haben dasselbe Verhältnis von Gegenkathete zu Hypotenuse : Sinus des Winkels α: sin α = a Gegenkathete = c Hypotenuse Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A I · α Ankathete b Weitere Verhältnisse: C Ankathete zu Hypotenuse Cosinus des Winkels α: cos α = b Ankathete = c Hypotenuse Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A I · α Ankathete b Weitere Verhältnisse: C Gegenkathete zu Ankathete Tangens des Winkels α: tan α = a Gegenkathete = b Ankathete Definitionen der Winkelfunktionen B Hypotenuse c Gegenkathete a A I · α Ankathete b Weitere Verhältnisse: C Ankathete zu Gegenkathete Cotangens des Winkels α: cot α = b Ankathete = a Gegenkathete Definitionen der Winkelfunktionen Sinus: Cosinus: 1 1 0 0 0 o o 90 o 180 o 270 o 360 -1 0 o o 90 o 180 o 270 o 360 -1 Tangens: Cotangens: 0 0 0 o o 90 o 180 o 270 o 360 0 o o 90 o 180 o 270 o 360 Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = a c 1 sin α a = · = sin α · = b c b cos α cos α Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = a c 1 sin α a = · = sin α · = b c b cos α cos α Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = a c 1 sin α a = · = sin α · = b c b cos α cos α Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = a c 1 sin α a = · = sin α · = b c b cos α cos α Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = I a c 1 sin α a = · = sin α · = b c b cos α cos α Mit Hilfe des Satzes von Pythagoras: a2 + b 2 = c 2 ⇒ 2 2 a b + = 1 ⇒ sin2 α + cos2 α = 1 c c Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = I a c 1 sin α a = · = sin α · = b c b cos α cos α Mit Hilfe des Satzes von Pythagoras: a2 + b 2 = c 2 ⇒ 2 2 a b + = 1 ⇒ sin2 α + cos2 α = 1 c c Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: tan α = I a c 1 sin α a = · = sin α · = b c b cos α cos α Mit Hilfe des Satzes von Pythagoras: a2 + b 2 = c 2 ⇒ 2 2 a b + = 1 ⇒ sin2 α + cos2 α = 1 c c Einfache trigonometrische Beziehungen c a · α b I Durch Erweitern des Verhältnisses für den Tangens: a c 1 sin α a = · = sin α · = b c b cos α cos α tan α = I Mit Hilfe des Satzes von Pythagoras: a2 + b 2 = c 2 ⇒ I 2 2 a b + = 1 ⇒ sin2 α + cos2 α = 1 c c Inverse Funktionen: a c b cos α = c sin α = ⇒ ⇒ a =α c b arccos = α c arcsin Berechnungen in einem beliebigen Dreieck I Wie berechnet man fehlende Seiten und Winkel in einem beliebigen nicht rechtwinkligen Dreieck? ⇒ Mit Hilfe des Sinus- und Kosinussatzes Berechnungen in einem beliebigen Dreieck I Beispiel 1: Es sei a, α, β gegeben, berechne die Seite b. C b =? A α a β B Berechnungen in einem beliebigen Dreieck I Beispiel 1: Es sei a, α, β gegeben, berechne die Seite b. C a b =? h A I α · D β B Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck ADC : BDC : h ⇒ h = b · sin α b h sin β = ⇒ h = a · sin β a sin α = Berechnungen in einem beliebigen Dreieck I Beispiel 1: Es sei a, α, β gegeben, berechne die Seite b. C a b =? h A I α · D β B Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck ADC : BDC : h ⇒ h = b · sin α b h sin β = ⇒ h = a · sin β a sin α = Berechnungen in einem beliebigen Dreieck I Beispiel 1: Es sei a, α, β gegeben, berechne die Seite b. C a b =? h A I α · D β B Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck ADC : BDC : h ⇒ h = b · sin α b h sin β = ⇒ h = a · sin β a sin α = Berechnungen in einem beliebigen Dreieck I Beispiel 1: Es sei a, α, β gegeben, berechne die Seite b. C a b =? h A I α · D β B Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck ADC : BDC : h ⇒ h = b · sin α b h sin β = ⇒ h = a · sin β a sin α = woraus a · sin β = b · sin α folgt. Berechnungen in einem beliebigen Dreieck I Beispiel 1: Es sei a, α, β gegeben, berechne die Seite b. C a b =? h A α · D Sinussatz a b c = = sin α sin β sin γ oder alternativ a : b : c = sin α : sin β : sin γ. β B Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C γ a b A c =? B Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C D γ · b a A I B c =? Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck BCD : h ⇒ h = a · sin γ a b1 cos γ = ⇒ b1 = a · cos γ a b1 cos γ = ⇒ b2 = b − b1 a sin γ = Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C D γ · a b h A I B c =? Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck BCD : h ⇒ h = a · sin γ a b1 cos γ = ⇒ b1 = a · cos γ a b1 cos γ = ⇒ b2 = b − b1 a sin γ = Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C b1 γ D · a b h A I B c =? Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck BCD : h ⇒ h = a · sin γ a b1 cos γ = ⇒ b1 = a · cos γ a b1 cos γ = ⇒ b2 = b − b1 a sin γ = Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C b1 γ D · a b b2 h A I B c =? Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Teildreieck BCD : h ⇒ h = a · sin γ a b1 cos γ = ⇒ b1 = a · cos γ a b1 cos γ = ⇒ b2 = b − b1 a sin γ = Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C b1 γ D · a b b2 h A I B c =? Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Satz von Pythagoras: c 2 = b22 + h2 = ... = a2 + b 2 − 2a · b · cos γ Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C b1 γ D · a b b2 h A I B c =? Idee: Zerlege das Dreieck in rechtwinklige Teildreiecke Satz von Pythagoras: c 2 = b22 + h2 = ... = a2 + b 2 − 2a · b · cos γ Berechnungen in einem beliebigen Dreieck I Beispiel 2: Es seien zwei Seiten a, b und der dazwischen liegende Winkel γ gegeben, berechne c. C b1 γ D · a b b2 h A c =? Kosinussatz c 2 = a2 + b 2 − 2a · b · cos γ Verallgemeinerung des Satzes von Pythagoras B Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 45◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 90◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 135◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 180◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 225◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 270◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 315◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 360◦ Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 360◦ I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 360◦ Winkel im Bogenmass 2π I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 315◦ Winkel im Bogenmass 7π/4 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 270◦ Winkel im Bogenmass 3π/2 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 225◦ Winkel im Bogenmass 5π/4 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 180◦ Winkel im Bogenmass π I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 135◦ Winkel im Bogenmass 3π/4 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 90◦ Winkel im Bogenmass π/2 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 45◦ Winkel im Bogenmass π/4 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Winkel können im Gradmass angegeben werden: Winkel im Gradmass 0◦ Winkel im Bogenmass 0 I . . . oder im Bogenmass = Bogenlänge im Einheitskreis. Winkelmasse I Umrechnung vom Bogenmass ins Winkelmass und umgekehrt: b Winkel im Gradmass β β Winkel im Bogenmass b Umrechnung: β = 360◦ · b 2π ⇐⇒ b = 2π · β 360◦