02.12.13 1
Werbung

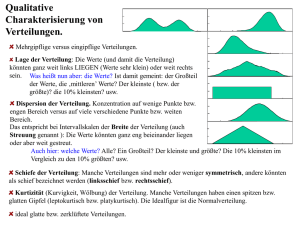
02.12.13 DAS THEMA: VERTEILUNGEN – LAGEMAßE STREUUUNGSMAßE • • • • Anteile – Häufigkeiten – Verteilungen Lagemaße Streuungsmaße Merkmale von Verteilungen VL Methodenlehre I WS13/14 Schäfer Anteile – Häufigkeiten – Verteilungen • Anteile und Häufigkeiten • Darstellung von Anteilen und Häufigkeiten • Nicht alle sind gleich – Verteilungen von Daten VL Methodenlehre I WS13/14 Schäfer 1 02.12.13 ANTEILE UND HÄUFIGKEITEN • das Skalenniveau, auf dem Daten gemessen wurden, entscheidet über das Format der Daten und damit über ihre weitere „Verwertbarkeit“ • schon ab Nominalskalenniveau können Anteile und Häufigkeiten bestimmt werden • Beispiele für Nominalskalen: von 50 Probanden sind 20 weiblich à Frauenanteil = 40%; von 50 Personen bevorzugen (aus Rock, Rap und Klassik) 30 Rockmusik à 60%, 15 Rap à 30% und 5 Klassik à 10% Häufigkeit Anteil VL Methodenlehre I WS13/14 Schäfer ANTEILE UND HÄUFIGKEITEN • Beispiele für Ordinaldaten: von 50 Probanden wählen (wenn sie für Rock, Rap, Klassik eine Rangreihen angeben sollen) 25 Rock auf Platz 1à 50%, 15 auf Platz 2 à 30%, 10 auf Platz 3 à 20%, usw. • Beispiele für Intervalldaten: von 50 Probanden kreuzen 5 einen Wert von 5 an à 10%, 4 einen Wert von 4 à 8% usw. usw. • ab Ordinalskalenniveau ist es offenbar nicht mehr besonders effizient, Daten in Anteilen und Häufigkeiten darzustellen VL Methodenlehre I WS13/14 Schäfer 2 02.12.13 DARSTELLUNG VON ANTEILEN UND HÄUFIGKEITEN • im Text: „Frauenanteil von 40 Prozent“ • in Tabellen: • in Abbildungen: Kreisdiagramm Histogramm (Häufigkeitsdiagramm) VL Methodenlehre I WS13/14 Schäfer NICHT ALLE SIND GLEICH – VERTEILUNGEN • Personen verteilen sich in ihren Messwerten, Urteilen usw. auf die möglichen Ausprägungen einer gemessenen Variable • es entstehen Verteilungen von Daten • sie beinhalten die wertvolle Information über die Variabilität von Merkmalen • in Häufigkeitsverteilungen sind die Werte einzelner Personen abgetragen z.B. für die Nominalskala: z.B. für die Intervallskala: usw. Person 3 Person 2 Person 1 VL Methodenlehre I WS13/14 Schäfer 3 02.12.13 Lagemaße • • • • Modus Median Mittelwert der Sinn der Lagemaße VL Methodenlehre I WS13/14 Schäfer LAGEMAßE • Häufigkeitsverteilungen konzentrieren sich (meist) bei bestimmten Ausprägungen • man spricht auch von der zentralen Tendenz • man kann daher die „Lage“ von Verteilungen auf der Achse der möglichen Ausprägungen eines Merkmals bestimmen und dafür Lagemaße angeben • je nach Skalenniveau können drei Lagemaße angegeben werden: Modus, Median, Mittelwert VL Methodenlehre I WS13/14 Schäfer 4 02.12.13 MODUS (MODALWERT) Welche Merkmalsausprägung kommt am häufigsten vor? möglich ab: Nominalskalenniveau Modalwert VL Methodenlehre I WS13/14 Schäfer MEDIAN (MD) Welche Merkmalsausprägung liegt in der Mitte der Verteilung? sinnvoll ab: Ordinalskalenniveau wie findet man den Median? 1. alle Werte der Größe nach aufschreiben 2. der Wert in der Mitte ist der Median 3. (liegt die Mitte zwischen 2 Werten, gilt der Mittelwert dieser beiden) Median VL Methodenlehre I WS13/14 Schäfer 5 02.12.13 MEDIAN (MD) der Median ist gegenüber der Schiefe einer Verteilung relativ unanfällig (robust) Modus: 3; Md: 3 Modus: 4; Md: 3 VL Methodenlehre I WS13/14 Schäfer MITTELWERT (ARITHMETISCHES MITTEL, M) Wo ist die mathematische Mitte der Verteilung? Mittelwert = Summe aller Einzelwerte, geteilt durch die Anzahl dieser Werte sinnvoll ab: Intervallskalenniveau Querstrich weist auf MiJelwert hin X oder M stehen für MiJelwert Summenzeichen x steht für Einzelwerte i ist der Index für das mehrfache Vorhandensein von Werten N ist die SPchprobengröße für das Beispiel: à der Mittelwert liefert die exakteste Angabe der Lage einer Verteilung VL Methodenlehre I WS13/14 Schäfer 6 02.12.13 MITTELWERT (ARITHMETISCHES MITTEL, M) VL Methodenlehre I WS13/14 Schäfer MITTELWERT (ARITHMETISCHES MITTEL, M) Aber: der Mittelwert ist anfällig gegenüber Ausreißern (besonders ungewöhnliche Werte) und schiefen Verteilungen Modus: 1; Md: 1; M = 1,3 Modus: 1; Md: 1; M = 1,9 à Modalwert und Median sind robuster und können daher manchmal sinnvoller sein VL Methodenlehre I WS13/14 Schäfer 7 02.12.13 MITTELWERT (ARITHMETISCHES MITTEL, M) Warum ist die Berechnung des Mittelwertes auf Ordinalskalenniveau nicht sinnvoll? Noten von 1-­‐4 Wie unterscheiden sich zwei Noten? 1 1 2 2 Was genau würde man also miJeln? à Der MiJelwert gibt eine Präzision vor, die auf Ordinalskalenniveau schlicht nicht vorhanden ist. sehr gut 1 2 „wahre“ Leistung eines Schülers (empirisches RelaPv) 3 4 eher schlecht VL Methodenlehre I WS13/14 Schäfer DER SINN DER LAGEMAßE Warum sind Lagemaße so wichtig, wenn man sich auch einfach die Häufigkeitsverteilungen der Daten ansehen könnte? à die Lagemaße sollen Verteilungen zusammenfassen und stellvertretend für ihre zentrale Tendenz stehen; sie sind daher auch sparsamer à für weitere Berechnungen Anzahl Personen wird oft nur der Mittelwert gebraucht (z.B. Anzahl Personen 35 Musikstil Rating für Klassik Rock 1 2 Rap 3 4 Klassik 5 5 4 Rating 30 25 20 15 5 10 0 wenn es um Gruppenunterschiede geht) 3 2 1 0 Klassik Rock Rap Musikstile VL Methodenlehre I WS13/14 Schäfer 8 02.12.13 Streuungsmaße • • • • • • Warum Streuungsmaße? Spannweite Interquartilsabstand Varianz Standardabweichung Kennwerte und Parameter VL Methodenlehre I WS13/14 Schäfer WARUM STREUUNGSMAßE? Warum sollte man Lagemaßen nicht ohne Weiteres vertrauen? à Lagemaße geben zwar die zentrale Tendenz einer Verteilung wieder, nicht aber ihre Streuung à Informationen über die Varianz – und damit über die Verlässlichkeit des Lagemaßes – gehen verloren VL Methodenlehre I WS13/14 Schäfer 9 02.12.13 WARUM STREUUNGSMAßE? Beispiele für gleiche Mittelwerte und verschiedene Streuungen VL Methodenlehre I WS13/14 Schäfer WARUM STREUUNGSMAßE? • Fazit: zu jedem Lagemaß gehört ein Streuungsmaß! • Streuungsmaße sind erst ab Ordinalskalenniveau sinnvoll • je nach Skalenniveau können verschiedene Streuungsmaße bestimmt werden: Spannweite, Interquartilsabstand, Varianz, Standardabweichung VL Methodenlehre I WS13/14 Schäfer 10 02.12.13 SPANNWEITE (RANGE) • • Differenz aus kleinstem und größtem Wert wird z.B. bei der Angabe des Alters verwendet, um zu zeigen, wie die extremen Ausprägungen aussehen 5 – 1 = 4 3 – 3 = 0 5 – 1 = 4 5 – 1 = 4 VL Methodenlehre I WS13/14 Schäfer INTERQUARTILSABSTAND (IA) • Differenz aus dem 75%- und dem 25%-Quartil • wird verwendet um Ausreißer unberücksichtigt zu lassen • wird oft als Streuungsmaß zusammen mit dem Median angegeben Wie bestimmt man den Interquartilsabstand (IA)? 1. alle Werte der Größe nach aufschreiben 2. die Zahlenreihe in vier gleich große Abschnitte teilen à Quartile 3. der IA bestimmt sich aus den Werten, die bei 25 und 75 Prozent liegen 1. QuarPl 2. QuarPl 3. QuarPl 4. QuarPl 1 2 2 3 3 3 3 4 4 5 IA = 4 – 2 = 2 VL Methodenlehre I WS13/14 Schäfer 11 02.12.13 INTERQUARTILSABSTAND (IA) 4 – 2 = 2 3 – 3 = 0 5 – 1 = 4 4 – 2 = 2 VL Methodenlehre I WS13/14 Schäfer VARIANZ (S2) • die durchschnittliche quadrierte Abweichung aller Werte von ihrem gemeinsamen Mittelwert • • liefert die exakteste Angabe über die Streuung das Quadrieren verhindert, dass sich positive und negative Abweichungen aufheben • Beispiel: VL Methodenlehre I WS13/14 Schäfer 12 02.12.13 STANDARDABWEICHUNG (S) • durch das Quadrat lässt sich die Varianz oft schwer interpretieren • man verwendet daher die Wurzel, die Standardabweichung • diese drückt die Streuung in den Rohwerten der Skala aus • sie wird in der Regel durch SD abgekürzt (Standard Deviation) • die übliche Darstellung von Lage- und Streuungsmaßen in Forschungsarbeiten geschieht mit Hilfe von Mittelwert und Standardabweichung: M = ... (SD = ...) VL Methodenlehre I WS13/14 Schäfer STANDARDABWEICHUNG (S) 1,41 0 2,0 1,0 VL Methodenlehre I WS13/14 Schäfer 13 02.12.13 KENNWERTE UND PARAMETER • Angaben über Stichprobendaten heißen Kennwerte • ihre Symbole stehen in lateinischen Buchstaben • Angaben über Populationswerte heißen Parameter • ihre Symbole stehen in griechischen Buchstaben FÜR DIE PRAXIS VL Methodenlehre I WS13/14 Schäfer Merkmale von Verteilungen • das Gesetz der großen Zahl • Formen von Verteilungen • die Normalverteilung VL Methodenlehre I WS13/14 Schäfer 14 02.12.13 DAS GESETZ DER GROßEN ZAHL • Lage- und Streuungsmaße sind nur dann sinnvoll interpretierbar, wenn die Stichprobe, aus der sie stammen, die Population gut wiederspiegelt • das ist dann der Fall, wenn die Häufigkeitsverteilung die gleiche Form hat wie die Populationsverteilung Beispiel für Stichprobenziehungen aus einer Population • (Achtung 1: die Population ist simuliert, normalerweise kennen wir die Populationsverteilung nicht!) • (Achtung 2: die gezeigten Stichproben sind zufällig und können jedes Mal anders aussehen!) VL Methodenlehre I WS13/14 Schäfer DAS GESETZ DER GROßEN ZAHL DEFINITION Das Gesetz der großen Zahl: Je größer eine Stichprobe ist, desto stärker nähert sich die Verteilung der enthaltenden Daten (Häufigkeitsverteilung) der wahren Verteilung in der Population an. Daher gilt... • für Sie als Wissenschaftler/in: je größer die Stichprobe, desto besser! • für Sie als Leser/in: trauen Sie Daten aus großen Stichproben mehr als Daten aus kleinen Stichproben! VL Methodenlehre I WS13/14 Schäfer 15 02.12.13 FORMEN VON VERTEILUNGEN • normalerweise verteilen sich Werte etwa symmetrisch um ihre zentrale Tendenz (Glockenform) • Abweichungen können zufällig (z.B. durch Ausreißer) oder systematisch sein (z.B. durch Decken- oder Bodeneffekte: an einem der beiden Pole treten viele oder sogar die meisten Werte auf) und führen zu schiefen (unsymmetrischen) Verteilungen • besonders relevant bei Werten mit einem definierten Nullpunkt (z.B. Reaktionszeiten) • Beispiel für eine rechts-schiefe Verteilung: à die Berechnung von Mittelwerten ist bei sehr schiefen Verteilungen nicht sinnvoll VL Methodenlehre I WS13/14 Schäfer FORMEN VON VERTEILUNGEN • normalerweise konzentrieren sich die Werte einer Verteilung an einer Stelle à unimodale (eingipflige) Verteilung • oft gibt es aber zwei solche Stellen à bimodale Verteilung • oder noch mehr à multimodale Verteilung • entsprechend gibt es mehrere Modalwerte • besonders relevant bei polarisierenden Skalen (z.B. Einstellungen) • Beispiel für eine bimodale Verteilung: à die Berechnung von Mittelwerten ist nur bei unimodalen Verteilungen sinnvoll VL Methodenlehre I WS13/14 Schäfer 16 02.12.13 FORMEN VON VERTEILUNGEN der Zusammenhang zwischen Symmetrie, Gipfligkeit und Lagemaßen VL Methodenlehre I WS13/14 Schäfer DIE NORMALVERTEILUNG • die meisten Variablen folgen in der Population der Verteilung einer Gauss‘schen Glockenkurve, der Normalverteilung • sie ist symmetrisch und die Wahrscheinlichkeit von Werten sinkt zu beiden Seiten des Mittelwertes immer mehr ab à legt man die Annahme der Normalverteilung zugrunde, haben Mittelwert und Standardabweichung immer eine einheitliche Bedeutung à die meisten Analyseverfahren in der Statistik beruhen auf dieser Annahme VL Methodenlehre I WS13/14 Schäfer 17 02.12.13 VERTEILUNGEN - LAGE-/STREUUNGSMAßE STECKBRIEF • quantitative Daten lassen sich immer durch Häufigkeiten und Anteile darstellen • es entstehen Häufigkeitsverteilungen (Daten einzelner Personen oder Objekte) • Häufigkeitsverteilungen lassen sich durch ihre Lage auf der Merkmalsachse (Lagemaße) und ihre Streuung (Streuungsmaße) kennzeichnen • • Lage- und Streuungsmaße sollen die Verteilung stellvertretend repräsentieren in Forschungsarbeiten werden meist Mittelwert und Standardabweichung angegeben • Gesetz der großen Zahl: Häufigkeitsverteilungen aus größeren Stichproben gleichen eher der Populationsverteilung • Verteilungen können symmetrisch oder schief sein • Verteilungen können unimodal, bimodal oder multimodal sein • die meisten Variablen sind in der Population normalverteilt und lassen sich daher mit Mittelwert und Standardabweichung sinnvoll repräsentieren VL Methodenlehre I WS13/14 Schäfer 18