Netzwerke Betrachten Netzwerke für TCP/IP Pakete, Stromnetze, usw.

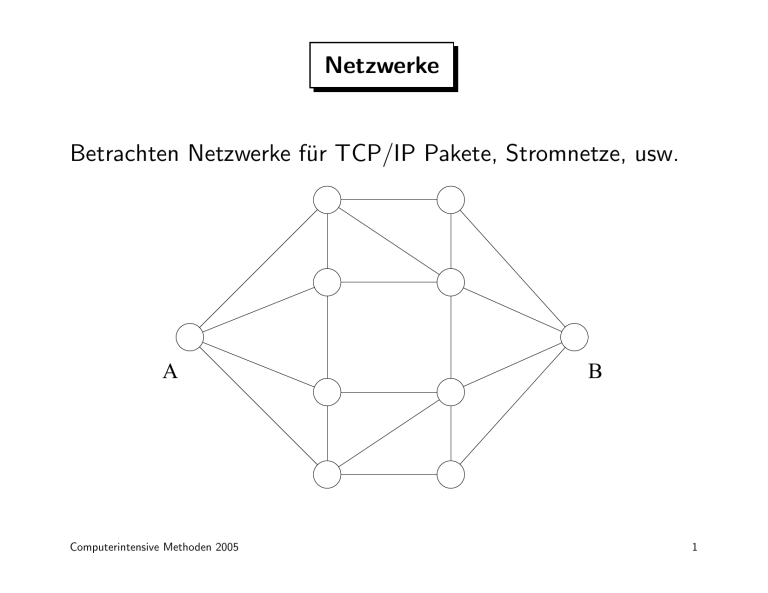
Netzwerke
Betrachten Netzwerke für TCP/IP Pakete, Stromnetze, usw.
A
Computerintensive Methoden 2005
B
1
Definitionen I
Jede Kante im Netzwerk kann – unabhängig von den anderen
Kanten – mit Wahrscheinlichkeit p ausfallen.
X = (X1, . . . , Xm),
Xi = I(die i’te Kante funktioniert)
Sei b(X) die Anzahl Kanten in X, die ausfallen.
Interesse an
0 falls A und B bei Konfiguration X verbunden
h(X) =
1 sonst.
Computerintensive Methoden 2005
2
Definitionen II
Im Beispiel m = 20 Kanten. Für X = (1, 0, 1, 0 . . . , 1, 0, 1, 0)
ist b(X) = 11 und h(X) = 0.
A
Computerintensive Methoden 2005
B
3
Wahrscheinlichkeit für Netzwerkstörung
Die Wahrscheinlichkeit für eine Netzwerkstörung ist
µ = E(h(X))
Die Berechunung von µ für ein Netzwerk kann eine sehr schwierige Kombinatorikaufgabe sein.
Computerintensive Methoden 2005
4
Monte-Carlo-Integration I
Ziehe X 1, . . . , X n iid. aus der Menge aller Netzwerkonfigurationen, bei denen eine Kante (unabhängig von den anderen
Kanten) mit Wahrscheinlichkeit p ausfällt. D.h.
X ij ∼ B(p) für j = 1, . . . , m
und
i = 1, . . . , n.
und somit
n
1X
h(X i)
µ̂MC =
n i=1
1
Var(µ̂MC) = µ(1 − µ)
n
Computerintensive Methoden 2005
5
Monte-Carlo-Integration II
h(X) kann mit dem Algorithmus von Floyd berechnet werden,
der den kürzesten Weg zwischen A und B bestimmt.
Für p = 0.05 und n = 105 bekommt man im Beispielsnetzwerk
µ̂MC = 3 · 10−5
se(µ̂MC) = 1.73 · 10−5.
Problem: h(X) nur sehr selten wenn p nicht unrealistisch groß.
Computerintensive Methoden 2005
6
Importance Sampling I
Simuliere X ∗1 , . . . , X ∗n mit Störwahrscheinlichkeit p∗ > p. Die
importance weights sind:
Qm x
ij (1 − p)1−xij
∗
p
f
(X
)
j=1
i
Q
w∗(X ∗i ) =
=
m
∗xij (1 − p∗)1−xij
g(X ∗i )
p
j=1
m b(X ∗i )
∗
p(1 − p )
1−p
=
1 − p∗
p∗(1 − p)
Der importance sampling Schätzer ist:
µ̂∗IS =
Computerintensive Methoden 2005
n
X
1
n i=1
h(X ∗i )w∗(X ∗i ).
7
Importance Sampling II
Für p∗ = 0.25, p = 0.05 und n = 105 bekommt man im
Beispielsnetzwerk
µ̂IS = 1.106 · 10−5
se(µ̂IS) = 4.664 · 10−7.
Computerintensive Methoden 2005
8