Brüche
Werbung
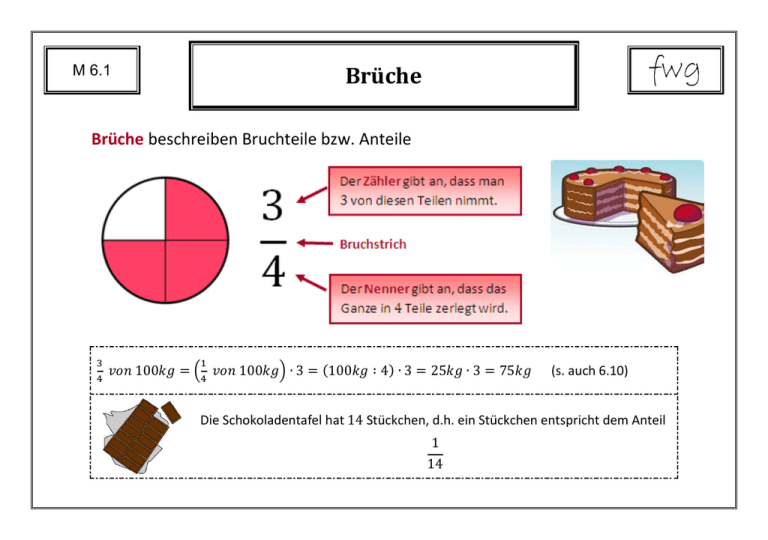
fwg Brüche M 6.1 Brüche beschreiben Bruchteile bzw. Anteile (s. auch 6.10) Die Schokoladentafel hat Stückchen, d.h. ein Stückchen entspricht dem Anteil M 6.2 Prozentschreibweise fwg Anteile werden häufig in Prozent angegeben. „1 Prozent“ heißt „1 Hundertstel“ Häufig vorkommende Prozentsätze – Lerne auswendig!! Nenner Nenner Nenner 5 Nenner fwg M 6.3 Kopfrechnen mit häufig vorkommenden Prozentsätzen Teile durch 10 Kommaverschiebung um eine Stelle Berechne 10 % und halbiere Berechne 10% und verdopple oder teile durch 5 Berechne 10 % und verdreifache M 6.4 Erweitern und Kürzen Durch Erweitern und Kürzen ändert sich der Wert des Bruches nicht. Kürzen Erweitern fwg fwg Rationale Zahlen M 6.5 Zahlen, die man durch Brüche angeben kann, heißen Bruchzahlen. Eine Bruchzahl kann durch verschiedene wertgleiche Brüche angegeben werden. ; ; ; Jede Bruchzahl hat einen Platz auf der Zahlengeraden. Die positiven und die negativen Bruchzahlen bilden zusammen mit der die Menge der rationalen Zahlen . M 6.6 Vergleichen rationaler Zahlen fwg Brüche können verglichen werden, indem man sie durch Erweitern oder Kürzen auf denselben Nenner oder auf denselben Zähler bringt: Gleiche Nenner: Der Bruch mit dem größeren Zähler ist größer Gleiche Zähler: Der Bruch mit dem kleineren Nenner ist größer Von zwei rationalen Zahlen ist diejenige größer, die weiter rechts auf der Zahlengeraden liegt (Beachte: pass auf bei negativen Zahlen z.B. !) M 6.7 Umwandeln von Brüchen in Dezimalbrüche fwg Bei Dezimalbrüchen bedeutet die erste Stelle nach dem Komma Zehntel, die zweite Hundertstel, die dritte Tausendstel,… … H Z T z h t 0 0 3 2 zt Methoden zum Umwandeln von Brüchen in Dezimalbrüche Erweitern oder Kürzen zu einem Bruch mit Stufenzahl im Nenner Schriftliches Dividieren Endlicher Dezimalbruch Unendlicher periodischer Dezimalbruch Enthält der Nenner eines vollständig gekürzten Bruches nur die Primfaktoren und , ergibt sich ein endlicher Dezimalbruch, andernfalls ein unendlicher. M 6.8 Relative Häufigkeit fwg Absolute Häufigkeit: Sie gibt an, wie oft ein bestimmtes Ergebnis auftritt. Relative Häufigkeit: Sie gibt an, bei welchem Anteil aller Versuche das bestimmte Ergebnis auftritt. Zufallsexperiment: -mal würfeln Absolute Häufigkeit für das Ergebnis „ “: Ergebnisse: Relative Häufigkeit für das Ergebnis „ “: Wiederholt man ein Zufallsexperiment sehr oft, so pendelt sich die relative Häufigkeit für jedes Ergebnis um einen bestimmten Wert ein (empirisches Gesetz der großen Zahlen). M 6.9 Addition und Subtraktion von Brüchen fwg Gleichnamige Brüche Zähler plus (minus) Zähler, Nenner beibehalten Ungleichnamige Brüche 1. Brüche gleichnamig machen (d.h. auf gleichen Nenner erweitern) 2. Gleichnamige Brüche addieren (subtrahieren) Der kleinstmögliche gemeinsame Nenner ist das kgV aller Nenner. Er heißt Hauptnenner ( Primfaktorzerlegung anwenden) Gemischte Zahlen 1. Gemischte Zahlen als Summen schreiben/denken 2. Ganze Zahlen zusammenrechnen, Brüche zusammenrechnen M 6.10 Multiplikation von Brüchen Bruch mal natürliche Zahl Zähler mal Zahl, Nenner beibehalten Bruch mal Bruch Zähler mal Zähler, Nenner mal Nenner Gemischte Zahlen 1. in unechte Brüche umwandeln 2. multiplizieren „Von“ bedeutet in der Bruchteil-Regel „mal“ fwg M 6.11 Division von Brüchen Bruch durch natürliche Zahl Nenner mal Zahl, Zähler beibehalten Bruch durch Bruch mit dem Kehrbruch multiplizieren Doppelbrüche In Division umschreiben fwg M 6.12 Rechnen mit Dezimalzahlen fwg Addieren und Subtrahieren Zahlen untereinander schreiben, so dass Komma unter Komma steht und stellenweise rechnen. Multiplizieren 1. Zahlen ohne Rücksicht auf die Kommas multiplizieren 2. Im Ergebnis das Komma so setzen, dass es so viele Nachkommastellen hat wie beide Faktoren zusammen Dividieren 1. In Dividend und Divisor das Komma so weit nach rechts verschieben, bis der Divisor eine natürliche Zahl ist (d.h. man erweitert mit einer Zehnerzahl!) 2. Überschreitet man beim Dividieren im Dividenden das Komma, wird im Ergebnis ein Komma gesetzt M 6.13 Einteilung von Brüchen und Dezimalbrüchen Brüche Unechte Brüche Zähler ist größer als Nenner → Umwandlung in gemischte Zahlen (=Summe aus ganzer Zahl und echtem Bruch) möglich Dezimalbrüche Echte Brüche Zähler ist kleiner als Nenner fwg Endliche Dezimalbrüche Unendliche periodische Dezimalbrüche reinperiodisch gemischtperiodisch Lerne auswendig!!! M 6.14 Parallelogramm fwg Flächenformeln Dreieck Trapez M 6.15 Schrägbilder fwg Die räumliche Darstellung eines Körpers nennt man Schrägbild. Beachte: Parallele Kanten bleiben parallel Senkrechte Kanten stehen im Schrägbild nicht mehr unbedingt senkrecht M 6.16 Der Oberflächeninhalt Netzes. Beispiel: Oberflächeninhalt fwg eines Körpers ist gleich dem Flächeninhalt seines Umrechnung von Länge, Fläche und Volumen M 6.17 Länge Umrechnungszahl Fläche Umrechnungszahl Volumen Umrechnungszahl Speziell: fwg M 6.18 Volumen des Quaders fwg fwg Prozentrechnung M 6.19 Aufgabentypen Prozentsatz gesucht Wie viel Prozent sind von Grundwert gesucht ? Prozentwert gesucht Wie viel sind vom Grundwert sind vom Grundwert sind vom Grundwert sind: von Schlussrechnung (Dreisatz) M 6.20 Äpfel kosten kosten ? . Wie viel fwg Dachdecker brauchen für ein Dach Stunden. Wie lange brauchen fünf Dachdecker? fwg Diagramme M 6.21 Säulendiagramm Balkendiagramm Kreisdiagramm Prozentstreifen