Addition und Subtraktion natürlicher Zahlen

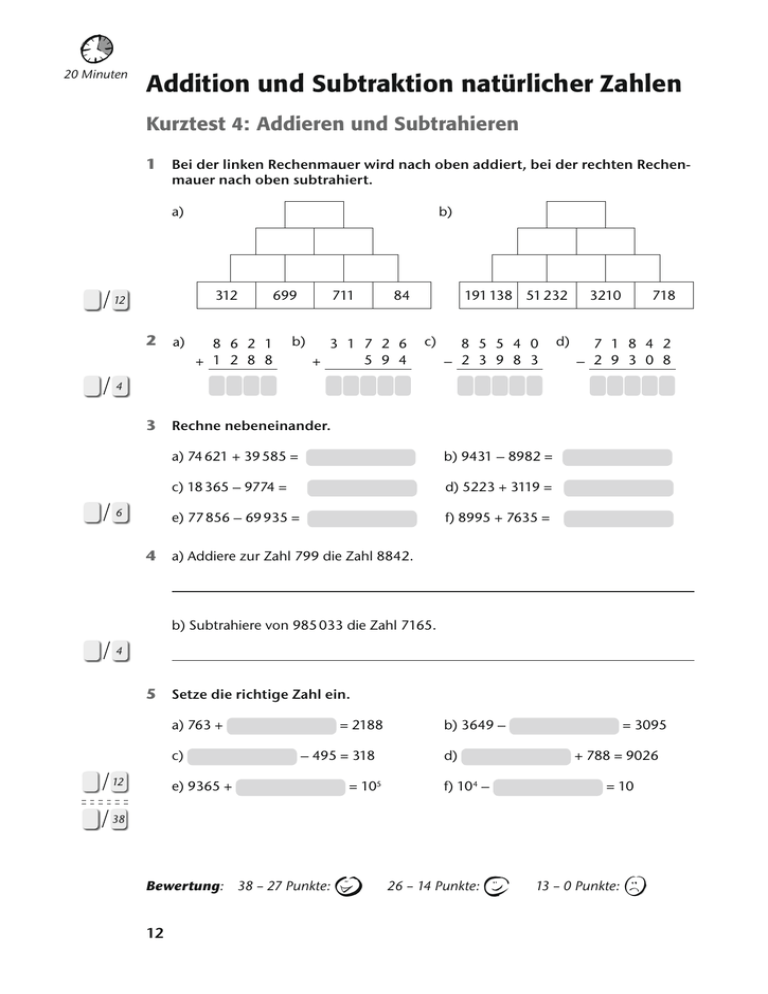
20 Minuten
Addition und Subtraktion natürlicher Zahlen
Kurztest 4: Addieren und Subtrahieren
1Bei der linken Rechenmauer wird nach oben addiert, bei der rechten Rechenmauer nach oben subtrahiert.
a)
b)
312
12
2 a)
699
8 6 2 1
+ 1 2 8 8
711
b)
84
191 138 51 232
c)
3 1 7 2 6
5 9 4
+
8 5 5 4 0
– 2 3 9 8 3
d)
3210
718
7 1 8 4 2
– 2 9 3 0 8
4
3 Rechne nebeneinander.
6
a) 74 621 + 39 585 =
b) 9431 – 8982 =
c) 18 365 – 9774 =
d) 5223 + 3119 =
e) 77 856 – 69 935 =
f) 8995 + 7635 =
4 a) Addiere zur Zahl 799 die Zahl 8842.
4
b) Subtrahiere von 985 033 die Zahl 7165.
5 Setze die richtige Zahl ein.
a) 763 +
c)
12
= 2188
– 495 = 318
e) 9365 +
= 105
b) 3649 –
d)
= 3095
+ 788 = 9026
f) 104 –
= 10
38
Bewertung: 38 – 27 Punkte:
12
X
26 – 14 Punkte:
Z
13 – 0 Punkte:
V
Kurztest 5: Vorteilhaftes Rechnen und Rechen­gesetze
20 Minuten
1Rechne vorteilhaft durch Vertauschen.
a) 393 + 468 + 107 =
4
b) 102 + 389 + 98 =
2Welches Rechengesetz wurde angewendet?
a) 1
52 + 99 + 18 = 152 + 18 + 99 = 170 + 99 = 269
b) 3
17 + (3 + 465) = (317+ 3) + 465 = 320 + 465 = 785
4
3Rechne geschickt im Kopf.
a) 82 + 59 + 111 + 118 =
4
b) 365 + 18 + 12 – 65 =
4Welche Aufgaben gehören zusammen, weil sie das gleiche Ergebnis haben?
Verbinde diese Paare mit einer Linie.
25 + 9
81 + 129
21 – 9
19 – 21
129 + 81
(18 – 3) +2
(64 + 3) +7
13 + (8 + 6)
18 – (3+2)
9 + 25
(13 + 8) + 6
64 + (7 + 3)
6
5Rechne vorteilhaft.
a) 702 + (98 + 16) =
b) 219 + 358 + 81 =
6
c) (83 + 59) + 17 =
6Familie Munter macht eine viertägige Radtour. Am ersten Tag fahren sie
63 km, am zweiten Tag 79 km, am dritten Tag 37 km und am vierten Tag
19 km weniger als am zweiten Tag. Wie lang war die Radtour?
4
Bewertung: 28 – 20 Punkte:
X
19 – 11 Punkte:
Z
10 – 0 Punkte:
28
V
13
20 Minuten
Kurztest 6: Gliedern und Berechnen von Termen
1Berechne und gliedere folgende Terme.
a) 14 + (81 – 6) =
b) (342 – 81) – (17 + 91) =
6
2Notiere zunächst den Term und berechne dann seinen Wert.
a) Subtrahiere von 966 die Differenz der Zahlen 169 und 93 und die Summe der
Zahlen 315 und 89.
b) Addiere die Summe der Zahlen 395 und 481 zur Differenz von 856 und 478.
8
3Stelle zum Rechenbaum den
Der Term ist
eine Differenz.
zugehörigen Term auf und
berechne seinen Wert.
Der Minuend
ist eine Summe.
Der 1. Summand ist 369.
4
Der Subtrahend
ist 715.
Der 2. Summand ist 577.
4Überschlage zuerst und berechne dann: 78 531 – [79 832 – (1985 + 3621)] =
Überschlag:
4
Rechnung:
5Berechne
a) 94406 – [(3655 + 4009) – 6089] =
b) (187 635 + 92 603) – (67 309 – 59 228) =
6
28
Bewertung: 28 – 19 Punkte:
14
X
18 – 10 Punkte:
Z
9 – 0 Punkte:
V
Abschlusstest 2
45 – 60 Minuten
1Ordne die folgenden Begriffe richtig zu: Minuend, 1. Summand, Wert der
Summe, Subtrahend, Wert der Differenz, 2. Summand.
a)6015
+ 3865
b)78 590
– 1590
= 9880
= 77 000
3
2Rechne vorteilhaft.
a) 1938 + 299 + 362 =
b) (555 + 97) + 45 =
3
c) 688 + (12 + 399) =
3Wie heißen die Rechengesetze?
a) F ür alle natürlichen Zahlen a, b gilt: a + b = b + a
– Gesetz der Addition
b) F ür alle natürlichen Zahlen a, b, c gilt: (a + b) + c = a + (b + c)
2
– Gesetz der Addition
4 a) W
ie groß ist der Wert der Differenz mit dem Minuenden 93 und dem
Subtrahenden 88?
b) U
m wie viel ist 715 kleiner als die Summe der Zahlen 1516 und 673?
c) A
ddiere die Differenz der Zahlen 5187 und 3799 zur Summe der Zahlen 897
und 798.
d) D
er Term ist eine Summe, deren 1. Summand eine Differenz mit dem
Minuenden 367 und dem Subtrahenden 239 ist. Der 2. Summand ist ein
Drittel der größten zweistelligen Quadratzahl.
8
15
5Berechne
a) 36 007 – [84 639 – (71 089 – 6854)] =
b) (5042 + 86 445) – (89 713 – 556) =
4
6 a) Wie ändert sich der Wert einer Differenz, wenn beide Zahlen um 5 vergrößert
werden?
b) Wie ändert sich der Wert einer Summe von drei Zahlen, wenn man jeden Summanden um 4 verkleinert?
c) W
ie ändert sich der Wert einer Differenz, wenn man den Subtrahenden um 2
verkleinert?
3
7Berechne und gliedere folgenden Term.
9385 – (384 + 999) =
3
8Setze Klammern so geschickt, dass der Term einen möglichst kleinen Wert
hat.
2
637 – 18 + 95 + 11 – 33 – 28 + 19
9Sind folgende Aussagen richtig? Gib bei einer falschen Aussage ein Gegenbeispiel an.
a) Der Wert der Summe zweier gerader Zahlen ist wieder eine gerade Zahl.
b) Der Wert der Summe zweier ungerader Zahlen ist wieder eine ungerade Zahl.
2
16
10Setze die richtigen Ziffern ein
a)
= 820
c)
6 – 91 = 3985
4 4 8
–
d)
b) 631 +
6
3 9 7
1 1
7
3 4
6 7
+ 1
8
e)
2
6
– 2 5
5
6 3 3
f)
3 7 9
6
8
1 3
+
3 6 4
g)
2
3 6
9 1
–
1 0 5 5 1
1 3 8
7
11Die Brüder Maxi, Tobias und Stefan haben zusammen 294 Fußballbilder. Maxi
hat doppelt so viele wie Tobias und Tobias hat doppelt so viele wie Stefan.
Wie viele Bilder hat jeder?
6
12 Überschlage zuerst und berechne dann.
a) 67 + 34 691 + 78 065 + 320 + 82 006 =
b) 102 340 + 672 + 11 199 + 7856 + 7 =
c) 58 978 + 8 366 501 + 641 722 + 358 =
6
13Gleiche Buchstaben bedeuten gleiche Ziffern. Finde sie. Eine Aufgabe ist
nicht lösbar. Begründe.
a)
+
DB A
B CA
b)
+
+
B A A A
A B B
CDB
+
8
E E F E
57
Bewertung: 57 – 39 Punkte:
X
38 – 20 Punkte:
Z
19 – 0 Punkte:
V
17
15 Minuten
Die ganzen Zahlen: Addition und Subtraktion
Kurztest 7: Negative Zahlen
1
1Welche der Zahlen 7; –1; 8; 0; 3; –10; 10; 2; ​ } 
 ​; –1000; –5 gehören zur Menge
2
N der natürlichen Zahlen, welche zur Menge Z der ganzen Zahlen? Trage ein.
Zu N gehören:
5
Zu Z gehören:
2Gib die ganzen Zahlen an, die durch die Pfeile markiert sind.
a)
–10
0
20
b)
6
–120
0
60
3Wähle auf der Zahlengerade eine geeignete Einheit und markiere die Zahlen.
a) 5; –11; 8; 0; –14; –6
b) –600; 300; 800; –100; 50; –400
10
4Herr Flotti hat 750 3 auf seinem Konto. Zuerst hebt er 490 3 für eine Schiausrüstung und kurz danach 280 3 für
eine neue Winterjacke ab.
Kann er sich von seinem Konto noch
Computerzubehör für 530 3 Leisten,
wenn er sein Konto nur um 500 3
überziehen darf?
4
25
Bewertung: 25 – 18 Punkte:
18
X
17 – 10 Punkte:
Z
9 – 0 Punkte:
V
Kurztest 8: Das Koordinatensystem
15 Minuten
1Schreibe die Koordinaten der eingezeichneten Punkte auf:
y
Gx
Jx
2
Fx
–4
Ex
3
–3
–2
Bx
Ax
1
–1 0
1
2
–1
H
x
Cx
I
x
3
x
4
Dx
A (
|
)
B (
|
)
C (
|
)
D (
|
)
E (
|
)
F
(
|
)
G (
|
)
H (
|
)
I (
|
)
J
|
)
(
5
–2
2 a) Z
eichne die Punkte A(0|–4), B(–3|–3), C(–5|0), D(–3|–1), E(–5|2), F(–1|–2),
G(–3|4), H(–1|2), I(0|4), J(0|1), K(2|4), L(1|0), M(5|1), N(1|–2), O(6|–2) und
P(0|–4) in das Koordinatensystem und verbinde sie in alphabetischer Reihenfolge.
y
4
3
2
1
–5
–4
–3
–2
–1 0
1
2
3
4
5
6
x
–1
–2
–3
–4
10
3
b) Welche Punkte liegen auf der y–Achse?
3In welchem Quadranten liegen die Punkte A(300|–18), B(–99|–100),
C(–60|60), D(75|2), E(8|81), F(–10|–1)?
Im I. Quadranten:
Im III. Quadranten:
Im II. Quadranten:
3
Im IV. Quadranten:
21
Bewertung: 21 – 15 Punkte:
X
14 – 8 Punkte:
Z
7 – 0 Punkte:
V
19
20 Minuten
Kurztest 9: Anordung, Betrag und Gegenzahl
1Ordne die folgenden Zahlen der Größe nach.
a) 23; 0; – 123; |–200|; 25; –2; 8; –19
<
<
<
<
<
<
<
<
<
<
<
b) 3; –52; –628; 15; 0; –18; |–8|; –4
<
8
<
<
2Trage die fehlenden Zahlen ein.
Vorgänger
Zahl
–22
–93
Nachfolger
7
21
0
0
–8
–15
3Welche Zahl liegt auf der Zahlengeraden genau in der Mitte zwischen den
beiden Zahlen?
4
a) –3 und 17
b) –25 und –91
c) 0 und –90
d) –18 und 46
4Gib jeweils die Gegenzahl an.
3
a) –17
b) 8
c) –11
d) 0
e) –5
f) 1
5Berechne.
10
a) |–75| + |75| =
b) |–3| + |–2| =
c) |–95| – |90| =
d) |–18| – 18 =
e) 27 – |–27| =
f) |42| · ||–5| · |–2|| =
g) 4 · |8–3| =
h) |9–5| · |–5| =
i) |–1| · |–1| · |–2| =
k) |2–1–1| =
32
Bewertung: 32 – 22 Punkte:
20
X
21 – 11 Punkte:
Z
10 – 0 Punkte:
V