rechenregeln_interne..
Werbung
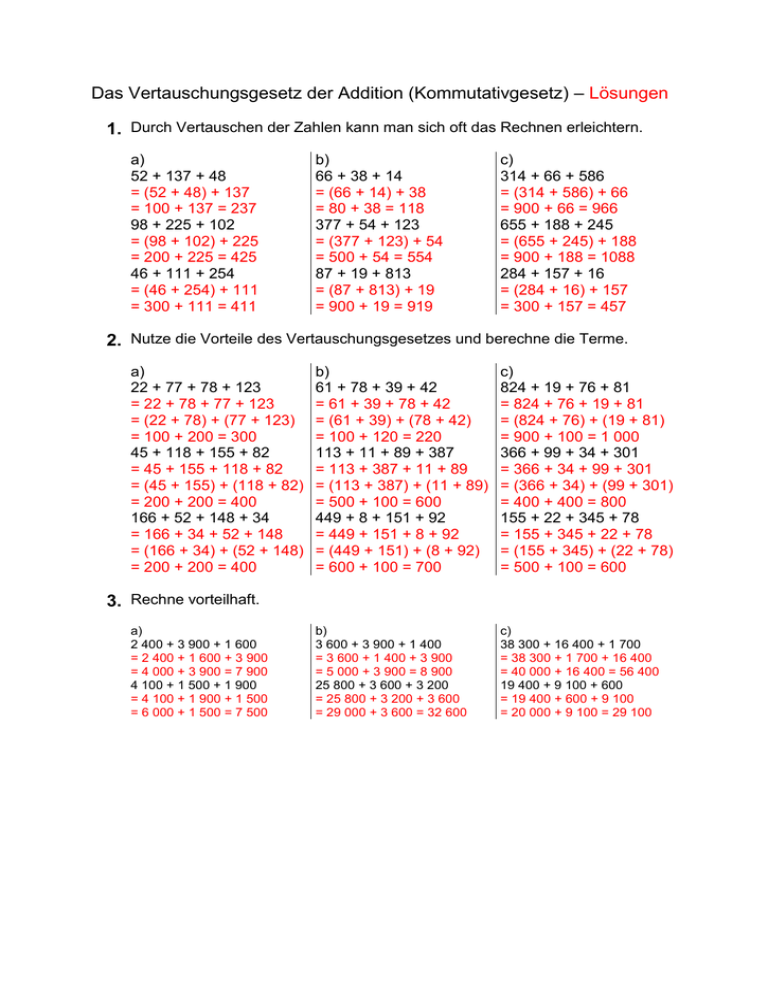
Das Vertauschungsgesetz der Addition (Kommutativgesetz) – Lösungen 1. Durch Vertauschen der Zahlen kann man sich oft das Rechnen erleichtern. a) 52 + 137 + 48 = (52 + 48) + 137 = 100 + 137 = 237 98 + 225 + 102 = (98 + 102) + 225 = 200 + 225 = 425 46 + 111 + 254 = (46 + 254) + 111 = 300 + 111 = 411 b) 66 + 38 + 14 = (66 + 14) + 38 = 80 + 38 = 118 377 + 54 + 123 = (377 + 123) + 54 = 500 + 54 = 554 87 + 19 + 813 = (87 + 813) + 19 = 900 + 19 = 919 c) 314 + 66 + 586 = (314 + 586) + 66 = 900 + 66 = 966 655 + 188 + 245 = (655 + 245) + 188 = 900 + 188 = 1088 284 + 157 + 16 = (284 + 16) + 157 = 300 + 157 = 457 2. Nutze die Vorteile des Vertauschungsgesetzes und berechne die Terme. a) 22 + 77 + 78 + 123 = 22 + 78 + 77 + 123 = (22 + 78) + (77 + 123) = 100 + 200 = 300 45 + 118 + 155 + 82 = 45 + 155 + 118 + 82 = (45 + 155) + (118 + 82) = 200 + 200 = 400 166 + 52 + 148 + 34 = 166 + 34 + 52 + 148 = (166 + 34) + (52 + 148) = 200 + 200 = 400 b) 61 + 78 + 39 + 42 = 61 + 39 + 78 + 42 = (61 + 39) + (78 + 42) = 100 + 120 = 220 113 + 11 + 89 + 387 = 113 + 387 + 11 + 89 = (113 + 387) + (11 + 89) = 500 + 100 = 600 449 + 8 + 151 + 92 = 449 + 151 + 8 + 92 = (449 + 151) + (8 + 92) = 600 + 100 = 700 c) 824 + 19 + 76 + 81 = 824 + 76 + 19 + 81 = (824 + 76) + (19 + 81) = 900 + 100 = 1 000 366 + 99 + 34 + 301 = 366 + 34 + 99 + 301 = (366 + 34) + (99 + 301) = 400 + 400 = 800 155 + 22 + 345 + 78 = 155 + 345 + 22 + 78 = (155 + 345) + (22 + 78) = 500 + 100 = 600 b) 3 600 + 3 900 + 1 400 = 3 600 + 1 400 + 3 900 = 5 000 + 3 900 = 8 900 25 800 + 3 600 + 3 200 = 25 800 + 3 200 + 3 600 = 29 000 + 3 600 = 32 600 c) 38 300 + 16 400 + 1 700 = 38 300 + 1 700 + 16 400 = 40 000 + 16 400 = 56 400 19 400 + 9 100 + 600 = 19 400 + 600 + 9 100 = 20 000 + 9 100 = 29 100 3. Rechne vorteilhaft. a) 2 400 + 3 900 + 1 600 = 2 400 + 1 600 + 3 900 = 4 000 + 3 900 = 7 900 4 100 + 1 500 + 1 900 = 4 100 + 1 900 + 1 500 = 6 000 + 1 500 = 7 500 4. Vertausche geschickt wie im Beispiel; fasse danach zusammen. 33 56 27 44 55 33 27 56 44 55 (33 27) (56 44) 55 60 100 55 215 a) 256 + 314 + 114 + 95 + 56 = 256 + 314 + 114 + 56 + 95 = (256 + 314) + (114 + 56) + 95 = 570 + 170 + 95 = 835 c) 615 + 338 + 45 + 66 + 42 = 615 + 45 + 338 + 42 + 66 = (615 + 45) + (338 + 42) + 66 = 660 + 380 + 66 = 1 106 e) 268 + 245 + 50 + 232 + 335 = 268 + 232 + 245 + 335 + 50 = (268 + 232) + (245 + 335) + 50 = 500 + 580 + 50 = 1 130 g) 438 + 511 + 122 + 119 + 68 = 438 + 122 + 511 + 119 + 68 = (438 + 122) + (511 + 119) + 68 = 560 + 630 + 68 = 1 258 b) 186 + 315 + 22 + 104 + 68 = 186 + 104 + 22 + 68 + 315 = (186 + 104) + (22 + 68) + 315 = 290 + 90 + 315 = 695 d) 212 + 53 + 147 + 99 + 888 = 212 + 888 + 53 + 147 + 99 = (212 + 888) + (53 + 147) + 99 = 1100 + 200 + 99 = 1 399 f) 333 + 222 + 217 + 59 + 148 = 333 + 217 + 222 + 148 + 59 = (333 + 217) + (222 + 148) + 59 = 550 + 370 + 59 = 979 h) 389 + 5 + 216 + 111 + 104 = 389 + 111 + 216 + 104 + 5 = (389 + 111) + (216 + 104) + 5 = 500 + 320 + 5 = 825 Das Verbindungsgesetz der Addition (Assoziativgesetz) – Lösungen 1. Berechne und vergleiche. a) (13 + 18) + 15 und 13 + (18 + 15) (13 + 18) + 15 13 + (18 + 15) = 31 + 15 = 13 + 33 = 46 = 46 c) (27 – 12) – 3 und 27 – (12 – 3) (27 – 12) – 3 27 – (12 – 3) = 15 – 3 = 27 – 9 = 12 = 18 b) (16 + 32) + 48 und 16 + (32 + 48) (16 + 32) + 48 16 + (32 + 48) = 48 + 48 = 16 + 80 = 96 96 d) (100 – 50) – 20 und 100 – (50 – 20) (100 – 50) – 20 100 – (50 – 20) = 50 – 20 = 100 – 30 = 30 = 70 2. Zeichne zu den Aufgaben aus Nr. 1 jeweils einen Rechenbaum. a) b) c) d) 3. Welche Gesetzmäßigkeit kannst du aus den Ergebnissen von Aufgabe 1 ableiten? Bei der Addition darf man Klammern beliebig setzen. Bei der Subtraktion ist dies nicht erlaubt, da es zu verschiedenen Ergebnissen führt. 4. Tauchen in Termen keine Klammern auf, so rechnet man von links nach rechts. Mit Hilfe des Verbindungsgesetzes kann man oft vorteilhaft rechnen. Setze deshalb in den folgenden Beispielen geeignete Klammen und berechne die Terme. a) 55 + 33 + 67 b) 112 + 277 + 23 c) 384 + 69 + 31 = 55 + (33 + 67) = 112 + (277 + 23) = 384 + (69 + 31) = 55 + 100 = 155 = 112 + 300 = 412 = 384 + 100 = 484 d) 881 + 99 + 1 e) 345 + 87 + 13 f) 212 + 147 + 53 = 881 + (99 + 1) = 345 + (87 + 13) = 212 + (147 + 53) = 881 + 100 = 981 = 345 + 100 = 445 = 212 + 200 = 412 5. Rechne vorteilhaft. Setze vorher Klammern. a) 33 + 67 + 155 = (33 + 67) + 155 = 100 + 155 = 255 62 + 38 + 413 = (62 + 38) + 413 = 100 + 413 = 513 19 + 56 + 44 = 19 + (56 + 44) = 19 + 100 = 119 d) 699 + 301 + 777 = (699 + 301) + 777 = 1 000 + 777 = 1777 924 + 555 + 445 = 924 + (555 + 445) = 924 + 1000 = 1 924 264 + 336 + 918 = (264 + 336) + 918 = 600 + 918 = 1 518 b) 287 + 113 + 499 = (287 + 113) + 499 = 400 + 499 = 899 333 + 265 + 135 = 333 + (265 + 135) = 333 + 400 = 733 508 + 192 + 189 = (508 + 192) + 189 = 700 + 189 = 889 e) 2 185 + 315 + 4 012 = (2 185 + 315) + 4 012 = 2 500 + 4 012 = 6 512 7 266 + 1 812 + 188 = 7 266 + (1 812 + 188) = 7 266 + 2 000 = 9 266 3 097 + 4 216 + 1 784 = 3 097 + (4 216 + 1 784) = 3 097 + 6 000 = 9 097 c) 913 + 87 + 412 = (913 + 87) + 412 = 1 000 + 412 = 1 412 844 + 156 + 317 = (844 + 156) + 317 = 1 000 + 317 = 1 317 555 + 388 + 412 = 555 + (388 + 412) = 555 + 800 = 1 355 f) 3 698 + 4 002 + 563 = (3 698 + 4 002) + 563 = 7 700 + 563 = 8 263 1 235 + 5 765 + 1 800 = (1 235 + 5 765) + 1 800 = 7 000 + 1 800 = 8 800 1 644 + 9 012 + 1 988 = 1 644 + (9 012 + 1 988) = 1 644 + 11 000 = 12 644 Das Verbindungsgesetz der Multiplikation – Lösungen 1. Berechne und vergleiche. a) (30 5) 2 30 (5 2) a) (30 5) 2 b) 3 (5 6) (3 5) 6 b) 3 (5 6) c) (14 2) 5 14 (2 5) c) (14 2) 5 d) (300 5) 10 300 (5 10) d) (300 5) 10 150 2 300 3 30 90 28 5 140 1500 10 15000 30 (5 2) (3 5) 6 14 (2 5) 30 10 300 15 6 90 14 10 140 300 (5 10) 300 50 15000 2. Zeichne zu den Aufgaben aus Nr. 1 jeweils einen Rechenbaum. a) b) c) d) 3. Welche Gesetzmäßigkeit kannst du aus den Ergebnissen von Aufgabe 1 ableiten? Bei der Multiplikation darf man beliebig Klammern setzen. Das Ergebnis ändert sich dabei nicht. 4. Setze vorteilhaft Klammern und rechne aus. a) 40 5 11 b) 13 4 50 c) 19 25 8 d) 10 64 2 12 4 25 a) 40 5 11 (40 5) 11 200 11 2 200 250 4 88 b) 13 4 50 13 (4 50) 13 200 2 600 12 125 4 c) 19 25 8 19 (25 8) 19 200 3 800 12 4 50 d) 10 64 2 10 (64 2) 10 128 1 280 12 4 25 12 (4 25) 12 100 1 200 250 4 88 (250 4) 88 1000 88 88 000 12 125 4 12 (125 4) 12 500 6 000 12 4 50 12 (4 50) 12 200 2 400 5. Setze vorteilhaft Klammern und rechne aus. Denke auch an das Vertauschungsgesetz. a) 582 b) 19 5 2 c) 5 17 2 d) 5 3 9 20 27 50 2 a) 582 528 (5 2) 8 10 8 80 25 8 4 b) 19 5 2 19 (5 2) 19 10 190 4 23 5 c) 5 17 2 5 2 17 (5 2) 17 10 17 170 25 7 2 2 d) 5 3 9 20 5 20 3 9 (5 20) (3 9) 100 27 2 700 27 50 2 27 (50 2) 27 100 2 700 25 8 4 25 4 8 (25 4) 8 100 8 800 4 23 5 4 5 23 (4 5) 23 20 23 460 25 7 2 2 25 2 2 7 25 (2 2) 7 25 4 7 (25 4) 7 100 7 700 6. Berechne und vergleiche. a) (81 : 9) : 3 81 : (9 : 3) a) (81 : 9) : 3 =9:3=3 b) (96 : 12) : 2 96 : (12 : 2) b) (96 : 12) : 2 =8:2=4 c) (480 : 20) : 4 480 : (20 : 4) c) (480 : 20) : 4 = 24 : 4 = 6 d) (48 : 8) : 2 48 : (8 : 2) d) (48 : 8) : 2 =6:2=3 81 : (9 : 3) = 81 : 3 = 27 96 : (12 : 2) = 96 : 6 = 16 480 : (20 : 4) = 480 : 5 = 96 48 : (8 : 2) = 48 : 4 = 12 7. Welche Gesetzmäßigkeit kannst du aus den Ergebnissen von Aufgabe 6 ableiten? Das Verbindungsgesetz gilt nicht für die Division. 8. Rechne möglichst einfach. a) 5 11 6 b) 2 73 500 c) 5772 d) 6 50 9 20 4 13 5 a) 5 11 6 4 99 25 b) 2 73 500 2 500 73 (2 500) 73 1000 73 73 000 9 2 11 5 c) 5772 40 33 2 25 d) 6 50 9 20 5277 50 20 6 9 (50 20) (6 9) 10 49 490 1000 54 54 000 4 13 5 4 99 25 9 2 11 5 4 5 13 4 25 99 2 5 9 11 40 33 2 25 40 25 33 2 (4 5) 13 (4 25) 99 100 99 9 900 (2 5) (9 11) 5 6 11 (5 6) 11 30 11 330 20 13 260 (5 2) (7 7) 10 99 990 (40 25) (33 2) 1 000 66 66 000 9. Rechne möglichst einfach. a) 8 2 7 50 b) 8 9 7 125 c) 25 125 40 8 d) 13 500 9 2 5 8 14 20 a) 8 2 7 50 2 50 8 7 (2 50) (8 7) 100 56 5 600 7 4 3 125 b) 8 9 7 125 8 125 9 7 (8 125) (9 7) 1000 63 63 000 120 15 5 6 c) 25 125 40 8 25 40 125 8 (25 40) (125 8) 1 000 1 000 1 000 000 8 11 3 1250 d) 13 500 9 2 500 2 13 9 (500 2) (13 9) 1 000 117 117 000 5 8 14 20 5 20 8 14 7 4 3 125 4 125 7 3 120 15 5 6 120 5 15 6 8 11 3 1 250 8 1 250 11 3 (5 20) (8 14) 100 112 (4 125) (7 3) 500 21 (120 5) (15 6) 600 90 (8 1 250) (11 3) 10 000 33 11 200 10 500 54 000 330 000 Das Vertauschungsgesetz der Multiplikation (Kommutativgesetz) – Lösungen 1. Durch Vertauschen der Zahlen kann man sich oft das Rechnen erleichtern. a) 285 b) 4 30 125 c) 50 9 2 4 17 25 2 38 50 a) 285 258 10 8 80 8 9 125 20 7 5 b) 4 30 125 4 125 30 500 30 15 000 250 18 4 12500 9 8 c) 50 9 2 50 2 9 100 9 900 4 17 25 8 9 125 250 18 4 4 25 17 8 125 9 1 000 9 9 000 250 4 18 20 7 5 12 500 9 8 12 500 8 9 100 17 1 700 2 38 50 2 50 38 100 38 3 800 20 5 7 100 7 700 1 000 18 18 000 100 000 9 900 000 2. Nutze die Vorteile des Vertauschungsgesetzes und berechne die Terme. a) 2 17 5 2 b) 2 3 50 79 c) 11 125 2 8 19 4 3 25 9 25 8 4 a) 2 17 5 2 2 5 17 2 10 34 340 50 13 2 5 4 5 25 8 b) 2 3 50 79 2 50 3 79 100 237 23 700 4 43 2 25 5 23 4 3 c) 11 125 2 8 125 8 11 2 1 000 22 22 000 19 4 3 25 50 13 2 5 4 43 2 25 4 25 19 3 50 2 13 5 4 25 43 2 100 57 5 700 100 65 6 500 100 86 8 600 9 25 8 4 25 4 9 8 4 5 25 8 4 25 5 8 5 23 4 3 5 4 23 3 100 72 7 200 100 40 4 000 20 69 1 380 3. Rechne vorteilhaft. a) 4 6 7 25 b) 4 39 25 2 c) 11 250 3 4 25 7 2 2 25 9 4 3 a) 4 6 7 25 4 25 6 7 100 42 4 200 9 25 2 4 5 4 20 8 b) 4 39 25 2 4 25 39 2 100 78 7 800 8 2 5 125 16 20 7 5 c) 11 250 3 4 250 4 11 3 1 000 33 33 000 25 7 2 2 9 25 2 4 8 2 5 125 25 2 2 7 25 4 9 2 8 125 2 5 100 7 700 100 18 1 800 1 000 10 10 000 25 9 4 3 25 4 9 3 5 4 20 8 5 20 4 8 16 20 7 5 20 5 16 7 100 27 2 700 100 32 3 200 100 112 11 200 Das Verteilungsgesetz (Distributivgesetz) – Lösungen 1. Schreibe die Rechenbäume als Terme. Berechne und vergleiche. a) 34 32 12 6 18 b) 3 (4 2) 3 6 18 69 59 54 45 99 (6 5) 9 11 9 99 2. a) 9 3 5 3 (9 ? ) 3 b) 12 8 5 8 (12 ? ) 8 6 3 4 3 (6 ? ) 3 15 5 8 5 (15 ? ) 5 8 3 2 3 (8 2) ? a) 9 3 5 3 (9 5 ) 3 14 3 42 16 3 6 3 ( ? ? ) 3 b) 12 8 5 8 (12 5 ) 8 7 8 56 6 3 4 3 (6 4 ) 3 10 3 30 8 3 2 3 (8 2) 3 10 3 30 15 5 8 5 (15 8 ) 5 7 5 35 16 3 6 3 ( 16 6 ) 3 10 3 30 3. a) 15 6 11 6 ? 6 b) 14 5 7 5 ? 5 c) 260 6 60 6 ? 6 55 5 45 5 ? 5 18 3 6 3 ? 3 33 15 18 15 ? 15 47 3 3 3 ? 3 a) 15 6 11 6 26 6 19 6 12 6 ? 6 b) 14 5 7 5 7 5 c) 260 6 60 6 200 6 55 5 45 5 100 5 47 3 3 3 50 3 18 3 6 3 12 3 19 6 12 6 7 6 33 15 18 15 15 15 18 11 9 11 9 11 7 19 7 11 7 ? b) 45 79 45 21 45 ? c) 15 40 15 38 15 ? 6 23 6 27 6 ? 91 4 91 6 91 ? 11 91 11 9 11 ? a) 7 19 7 11 7 30 6 53 6 7 6 ? 4. a) b) 45 79 45 21 45 100 6 23 6 27 6 50 11 91 11 9 11100 91 4 91 6 9110 6 53 6 7 6 60 18 11 9 11 ? 11 7 97 7 95 7 ? 14 114 14 14 14 ? c) 15 40 15 38 15 2 7 97 7 95 7 2 14 114 14 14 14 100 5. Rechne wie im Beispiel: 3 7 6 7 9 7 63 a) 25 95 b) 5 60 6 60 c) 6 12 7 12 d) 6 105 3 105 73 83 3 53 4 53 4 18 4 18 6 304 2 304 45 65 9 81 2 81 2 25 3 25 2 122 3 122 99 49 8 60 3 60 3 43 5 43 5 401 4 401 a) 25 95 b) 5 60 6 60 c) 6 12 7 12 d) 6 105 3 105 11 5 55 11 60 660 13 12 156 9 105 945 73 83 15 3 45 3 53 4 53 7 53 371 4 18 4 18 8 18 144 6 304 2 304 8 304 2 432 45 65 9 81 2 81 2 25 3 25 10 5 50 11 81 891 5 25 125 2 122 3 122 5 122 610 99 49 13 9 117 8 60 3 60 11 60 660 3 43 5 43 8 43 344 5 401 4 401 c) 54 3 49 3 d) 85 13 83 13 17 5 8 5 69 27 64 27 30 2 28 2 99 11 91 11 46 4 44 4 c) 54 3 49 3 77 25 67 25 d) 85 13 83 13 5 3 15 2 13 26 9 401 3 609 6. Rechne wie im Beispiel: 34 5 4 5 30 5 150 a) b) 23 4 19 4 60 8 30 8 13 9 6 9 90 5 60 5 17 6 14 6 70 7 40 7 19 5 13 5 100 3 80 3 a) b) 23 4 19 4 60 8 30 8 4 4 16 30 8 240 13 9 6 9 7 9 63 90 5 60 5 30 5 150 17 5 8 5 9 5 45 69 27 64 27 5 27 135 17 6 14 6 70 7 40 7 30 2 28 2 99 11 91 11 3 6 18 30 7 210 22 4 8 11 88 19 5 13 5 6 5 30 100 3 80 3 20 3 60 46 4 44 4 24 8 77 25 67 25 10 25 250 7. Rechne möglichst einfach. Achte auf das Beispiel. ∙ 4 195 4 105 4 (195 105) 4 300 1 200 a) 12 88 12 12 b) 35 7 65 7 c) 8 (100 3) 7 (1000 8) 9 (200 6) 5 (300 15) c) 8 (100 3) d) (2000 4) 7 (100 13) 5 (300 6) 9 (400 11) 8 d) (2000 4) 7 7 73 7 27 81 13 9 13 19 97 19 3 87 12 13 12 48 127 48 73 a) 12 88 12 12 12 100 1 200 164 55 36 55 b) 35 7 65 7 100 7 700 8 100 8 3 824 2000 7 4 7 14 028 7 73 7 27 81 13 9 13 7 (1000 8) (100 13) 5 7 100 700 90 13 1170 7 1 000 7 8 7056 100 5 13 5 565 19 97 19 3 19 100 1 900 87 12 13 12 100 12 1 200 9 (200 6) 9 200 9 6 1854 (300 6) 9 300 9 6 9 2 754 48 127 48 73 48 200 9 600 164 55 36 55 5 (300 15) 200 55 11 000 5 300 5 15 1 575 (400 11) 8 400 8 11 8 3 288