Theoretische Grundlagen der Technischen Biologie

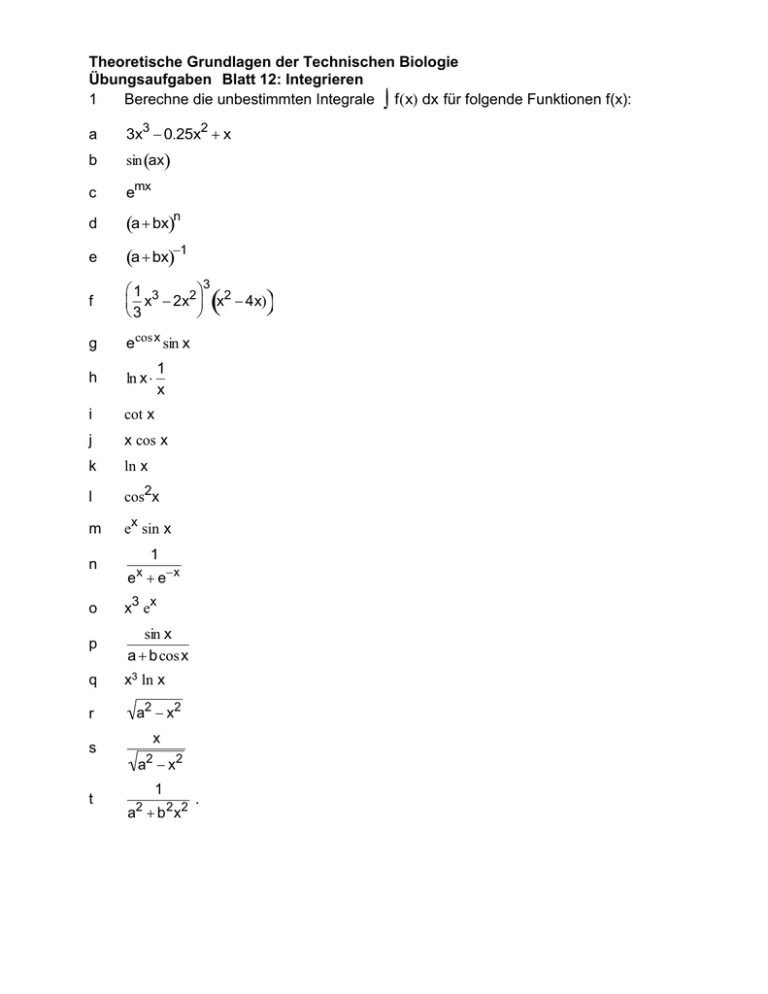
Theoretische Grundlagen der Technischen Biologie
Übungsaufgaben Blatt 12: Integrieren
1
Berechne die unbestimmten Integrale  f(x) dx für folgende Funktionen f(x):
a
3x3  0.25x2  x
b
sin ax

 c
emx
 d
a  bxn
 e
a  bx1

f
3
1 3
2  2
x

2x

 x  4x)
3

g
ecos x sin x

 h


cot x
j
x cos x
k
ln x
l
cos2x
m
ex sin x
n
e  ex
o
x3 ex
q
 r
s

t

1
x
ln x 
i
 p


1
x
sin x
a  b cos x
x3 ln x
a2  x2
x
a2  x2
1
2
a  b 2 x2
.

2
a
b

c

d

e

3
 a
Bestimme das unbestimmte Integral
Funktionen:
 f(x) dx
durch Partialbruchzerlegung für folgende
x3

2
x  4x  5
2x  6
2x2  3x  1
2x3 13
x2 10x  25
3x2  1
x2  4x  4
x2  3x 1
x3  x2  x 1
Berechne den Wert der nachstehenden bestimmten Integrale
2
 4xx2  x 1 x2 dx
0
2
b

 sin u du
0
x
c

 sin 2t  3 dt
0
x2
d

 a  b  ln u du
x1
1
e

 x2 dx2 ,
0
 1 fџr

 f(x)dx mit f(x)  0 fџr
1 fџr
1

1

f
3
g

4
0
2x  1
4x2  4x  1
x0
x0
x0
dx
x
h

mit f(0)=0.
0
4

 f(t) dt
In welchem Abstand  ist eine Parallele zur y–Achse zu ziehen, damit die von der x–
Achse, der y–Achse, der Geraden x=1 und der Kurve y=e x begrenzte Fläche im Verhältnis 1:2 geteilt wird?
5a
Berechne die Bogenlänge der Kurve y=cosh x zwischen x=0 und x=0.5 .
b
Das Kurvenstück sei mit der Dichte =1 belegt. Berechne ihren Kurvenschwerpunkt.
6a
Berechne das Volumen des Rotationskörpers, das entsteht, wenn man das Bogenstück
y=x2, 1≤x≤2, um die x–Achse dreht.
b
Berechne die Oberfläche des Rotationskörpers in a).
7
Berechne folgende uneigentlichen Integrale:
2
a
1
 3 x 1 dx
0

b

 x3 dx
1
4

1
c
Für welche  existiert das uneigentliche Integral
8
Um eine Feder auszudehnen, wird eine Kraft benötigt, die linear von der Ausdehnung x
abhängt:

 kg 
K(x)=D·x, worin D  10 2  sei.
sec 
a
Zerlege das Intervall [0,1] in 10 Teilintervalle [0,0.1], [0.1,0.2],..., [0.9,1]. Berechne unter
der vereinfachenden Annahme, daß in jedem Teilintervall [xi-1,xi], 1≤i≤10, eine konstante

x  x 
Kraft der Größe Ki  K i1 i  vorliegt, näherungsweise die Arbeit A(x), die geleistet
 2 
werden muß, um die Feder 1 m auszudehnen.
b
Stelle die Abhängigkeit der Arbeit A(x) von der Ausdehnung x durch ein bestimmtes Integral mitvariabler oberer Grenze x dar.
c
Berechne die in 7a) erfragte Arbeit exakt mit einer Stammfunktion.
9
Ein Hubkolben bewegt sich in einem Zylinder analog zu einer harmonischen Schwingung
2
periodisch mit der Geschwindigkeit v(t)  Asin t  , worin  
 2 die WinkelgeT
schwindigkeit, T=0.1 Sekunden die Zeitdauer für einen Zyklus (Frequenz =10) und A aus
der nachstehenden Bedingung zu errechnen ist. Zur Zeit t=0 und zur Zeit t=T befindet er
sich am Eingang x=0 des Zylinders.
Nach einem halben Zyklus (t=0.05) hat er sich bis zu


seinem Umkehrpunkt x=0.05 m vorwärts bewegt. Der Zylinder
hat den Durchmesser d=0.2
m und die Länge 0.06 m und ist mit Luft gefüllt. Der Hubkolben besitzt den gleichen Durchmesser d. In der Ausgangssituation t=0 herrscht im Zylinder der Druck 1 bar.
a
Bestimme die Kolbengeschwindigkeit v(t) und die Kolbenbewegung x(t) als Funktion der
Zeit.
b
Beschreibe die Kompression der Luft im Zylinder durch den Druck p=f(V)=g(x) bzw.
durch die Kraft auf den Kolben F=h(x), worin V das Zylindervolumen zwischen Kolben
und Zylinderwand und x den Kolbenweg bedeuten. Mache dabei folgende Annahmen: i)


2 x  2
dx ?
Der Prozess ist isotherm, ii) die Lufttemperatur ist T=T 0=300K, iii) die Luft ist ein ideales
Gas.
c
Definiere die vom Zylinderkolben geleistete Arbeit W für die isotherme Kompression zunächst näherungsweise durch eine Riemann–Summe und zerlege dabei den Prozess in
5 Teilintervalle. Verwende die Intervallmitten als Argumente zur Konstruktion einer Treppenfunktion, die p=f(V) approximieren soll.
d
Definiere die Kompressionsarbeit W durch ein bestimmtes Integral, in dem das EndvoludW(V)
men V als variable, obere Grenze steht. Bestätige die Beziehungen
 p(V) und
dV
dW(x)
 F(x) .
dx
e
Berechne die geleistete Kompressionsarbeit durch eine Berechnung
mit einer Stamm
funktion.
 f
8
Beschreibe die Kompressionsarbeit W(x(t)) als Funktion der Zeit. Definiere die Leistung.
Die Moleküle eines Gases bewegen sich mit unterschiedlichen Geschwindigkeiten. Die
Wahrscheinlichkeiten für das Auftreten der unterschiedlichen Geschwindigkeiten werden
durch die Maxwell-Boltzmann-Verteilungsfunktion beschrieben
mu2
 m 3 2  2kT
f(u)  4  
, 0  u < ,
 u  e
2kT 
worin m die Molekülmasse, k die Boltzmannkonstante und T die absolute Temperatur bedeuten.

a
Berechne die mittlere Geschwindigkeit: u 

 u  f(u) du .
0
b
Ein quaderförmiger Behälter der Größe V  x A mit der Länge x und der Seitenfläche A (senkrecht zur x–bzw. u–Richtung) enthalte N Moleküle des Gases. Berechne die
Anzahl N der Moleküle, die in
einem Zeitintervall t auf die Wand prallen.
c
Berechne daraus Impuls, Kraft und
 Druck an die Wand, wenn jedes Molekül beim Aufprall
den Impuls (2 m·u) abliefert.
