Molekulare und chemische Dynamik in flüssiger Phase Experimente

Molekulare und chemische Dynamik in flüssiger Phase
Experimente und Modelle
5. Vorlesung 11.11.2008
Quantenmechanik II
Harmonischer Oszillator, Schwingungsspektren
Peter Gilch
Lehrstuhl für BioMolekulare Optik
Fakultät für Physik
Ludwig-Maximilians-Universität München
Nachtrag: Dichtematix und zeitabhängige Störungen
Wir wollen mittels des Dichtematrix-Formalismus den Absorptionsprozess im
2-Niveau-System beschreiben. Der Absorptionsprozess kann mit einer zeitabhängige Störung V(t) beschrieben werden. Wir gehen von einem monochromatischen Lichtfeld aus, das wir klassisch behandeln.
Ea
Eb
Das System wechselwirkt über das elektrische oder magnetische Dipolmoment
mit dem elektrischen und magnetischen Feld. Wir nehmen an, dass die Basiszustände Φa und Φb keine Dipolmomente haben. Der zeitabhängige HamiltonOperator nimmt dann folgende Form an:
Die Liouville-Gl.
i
d
ρˆ (t ) = − [ Hˆ 0 , ρˆ (t )] (zunächst noch ohne Störung und
h
dt
Relaxation) lautet:
Mit der Lösung:
Wir „bauen“ die Phasenfaktoren in die Variablen ein:
Die Liouville-Gl.
dρ11
dt
dρ 22
dt
dρ~12
dt
dρ~21
dt
i
d
ρˆ (t ) = − [ Hˆ , ρˆ (t )] (mit Störung) lautet:
h
dt
i
= − E0 cos ωt ( µ12 e −iωt ρ~21 − µ 21eiωt ρ~12 )
h
i
= − E0 cos ωt ( µ 21e −iωt ρ~12 − µ12 e iωt ρ~21 )
h
i
= −iηρ~12 − E0 cos ωte −iωt µ12 ( ρ 22 − ρ11 )
h
i
= iηρ~12 − E0 cos ωte −iωt µ 21 ( ρ11 − ρ 22 )
h
Wir benutzen die „Rotating Frame Approximation“
Jetzt berücksichtigen wir longitudinale und transversale Relaxation:
Und erhalten die optischen Bloch-Gleichungen …
dρ z E 0 µ ~
=
ρ y − k r ( ρ z − ρ z ,eq )
dt
h
dρ~x
= −ηρ~y − k d ρ~x
dt
dρ~y
E0 µ
~
= ηρ x −
ρ z − k d ρ~y
dt
h
Von der Bloch-Gleichung zum Spektrum
Ea
Eb
Wir betrachten ein 2-Niveau-System,
das kontinuierlich mit monochromat.
Licht bestrahlt wird. Es stellt sich ein
stationärer Zustand ein, bei dem mit
konstanter Rate EM-Feldenergie in
Wärme umgewandelt wird.
Wie groß ist diese Rate, wie ist Ihre Frequenz-Abhängigkeit?
Stationaritätsbedingung für Bloch-Gl.:
dρ z E 0 µ ~
ρ y − k r ( ρ z − ρ z ,eq )
=
dt
h
dρ~x
= −ηρ~y − k d ρ~x
dt
dρ~y
Eµ
= ηρ~x − 0 ρ z − k d ρ~y
dt
h
… liefert Lorentz-Funktion:
Absorbierte Leistung
20
15
10
5
0
0
1
2
3
4
5
Frequenz ω
Das nächste Spielzeugsystem:
Der harmonische Oszillator
Der klassische und der quantenmechanische harmonische Oszillator ist in der
Molekülphysik omnipräsent.
Beispiele
Schwingungsspektroskopie
Elektrontransfer-Theorie
Infrarot
Raman
Aus W.W. Coblentz (1905)
Investigations of Infrared Spectra
Thermische
Bäder
Strahlungsfeld
Abschätzung zur harmonischen Näherung für die
Kernbewegung in Molekülen
Bei einem (stabilen) Molekül resultiert aus jeder Auslenkung ∆ri der Atomkerne
eine rücktreibende Kraft. Vornehmer: Ein Molekül ist ein (lokales) Minimum
auf einer Born-Oppenheimer (BO) Hyperfläche.
Die Kraft kann daher über das Hooksche Gesetz genähert werden
das Potenzial über eine Parabel
Für ∆ ri gegen null ist die Parabel sicher eine gute Näherung, wie es bei
typischen Auslenkungen aus?
Betrachten wir dazu ein zweiatomiges Molekül, z.B. HCl. Dessen BO-“Fläche“
ist eine Kurve, die sich mit dem Morse-Potenzial nähern lässt.
De Dissoziationsenergie, k harmonische Kraftkonstante
40000
Anharmonizität ist
35000
-1
Energie E [cm ]
30000
25000
20000
15000
10000
5000
0
0
1
2
3
4
5
Abstand HCl r [A]
Situation ist bei polyatomaren Molekülen noch „günstiger“, da bei der Auslenkung eines Atoms mehrere Bindungen rücktreibend wirken.
4000
-1
Energie E [cm ]
3000
2000
1000
0
1.15
1.20
1.25
1.30
Abstand HCl r [A]
1.35
1.40
Habil. Peter Gilch 2004
Zeitunabhängige Schrödinger-Gl. des
harmonischen Oszillators
Wir betrachten ein zweiatomiges Molekül, das durch die die Massen m1 und
m2 der beiden Atome, eines Gleichgewichtsabstandes x0 und einer Kraftkonstante k charakterisiert sei.
Im Folgenden legen wir den Ursprung der
Ortskoordinate auf den Gleichgewichtsabstand,
d.h. x0 = 0.
Die zeitunabhängige Schrödinger-Gl. für dieses Problem lautet:
Mit dimensionslosen Orts- und Impulsoperatoren (ω ist klassische Eigenfrequenz)
Lösung (Eigenwerte und -funktionen). Die Eigenfunktionen bilden (wie immer)
eine ONB.
Hn : Hermitsche Polynome, einige Beispiele
Nn : Normierungsfaktor
Typische Werte für ω und k
Einige Eigenschaften der Lösungen
- Energie-Niveaus äquidistant
- Nullpunktsenergie
- Zahl der Knoten steigt mit
der Quantenzahl n
- Verhalten wird mit n
„klassischer“
- Parität wechselt ab
- Erwartungswerte für die
Ortskoordinate x
Wie groß ist eine typische
Auslenkung für n=1?
http://www.pci.tu-bs.de/aggericke/PC3/Kap_III/Oszi_3.gif
Harmonischer Oszillator und
die zeitabhängige Schrödinger-Gl.
Wir untersuchen die Zeitentwicklung eines Zustandes χ(x,t), der kein Eigenzustand des harmonischen Oszillators ist. Dieser Zustand kann in der ONB
der Eigenfunktionen dargestellt werden:
Für die zeitabhängigen Entwicklungskoeffizienten cn(t) gilt:
Für alle Koeffizienten gilt:
Die Wellenfunktion ist periodisch mit T=2π/ω!
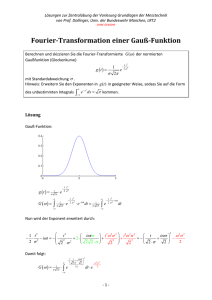
Wir betrachten den wichtigen Spezialfall, bei
dem die Funktion χ(x,t=0) durch eine verschobene Gauß-Funktion gegeben ist:
χ ( x, t = 0) =
Die Lösung lautet:
χ ( x, t ) =
Mit:
α −(1/ 2 )α
e
π
2
α −(1/ 2 )α
e
π
2
( x − x0 ) 2
[ x − x ( t )]2 + ( i / h ) p ( t )[ x − (1 / 2 ) x ( t )]
Vergleich mit klassischer
Schwingung
Zeitentwicklung der Aufenthaltswahrscheinlichkeit:
Wellenpakete und Femtosekunden-Spektroskopie
Die kohärente Überlagerung von Schwingungswellenfunktionen stellen ein
Wellenpaket dar. Ein Wellenpaket lässt sich durch elektronische Anregung
eines Moleküls (S0 →S1) mit einem kurzem Laserimpuls präparieren. Im
Zustand S1 sei die Kraftkonstante k unverändert, aber der GGW-Abstand
x0 größer.
S
1
S0
Präparation über
chemische Reaktion
T. Kühne, P. Vöhringer, J. Chem. Phys. 105 (1996) 10788
Schwingungen in polyatomaren Molekülen –
Normalmoden
Ein nicht-lineares Molekül mit N Atomen besitzt 3N-6 innere Freiheitsgrade.
Die potenzielle Energie hängt in der harmonischen Näherung wie folgt von
diesen Freiheitsgraden ab (wir legen wieder den Ursprung auf die GGWGeometrie):
Definition der Krafkonstante kij
Klassische Bewegungsgleichung
Massegewichtete Größen
Matrix-Darstellung
System von gekoppelten Differentialgleichungen. Es kann wieder durch Diagonalisierung mit Hilfe einer Matrix T aus Eigenvektoren gelösten werden.
Man erhält 3N-6 unabhängige harmonische Oszillatoren
Jeder Oszillator wird dann getrennt quantenmechanisch behandelt. Die
Gesamtwellenfunktion für die Schwingungen ergibt sich als Produkt.
Die Eigenvektoren bezeichnet man als Normalmoden. Die zugehörigen Bewegungen der Atome berechnen sich aus:
Beispiele: Normalmoden von H2O und CO2
Matrixelemente und Auf- und Absteigeoperatoren
Bei der Behandlung von Schwingungsspektren und der Schwingungsrelaxation
sind Matrixelemente der Form
von großer Bedeutung (Dipolmoment!)
In der harmonischen Näherung lassen sich diese Matrixelemente nach Einführung von Auf- und Absteigeoperatoren besonders leicht berechnen.
Wirkung dieser Operatoren (|n> = χn)
Ins Matrixelement eingesetzt:
{|n>} ist ONB
Damit gilt für einen Dipolübergang (~ |<n|x|n´>|2):
Experimentelle Methoden der
Schwingungsspektroskopie
Fluoreszenz- und
Absorptionspektroskopie
Raman-Spektroskopie
IR-Spektroskopie
Wellenpakete und
Fourier-Transformation
Schwingungsdaten aus
Absorption- und Emissionsspektren
In der Absorption- und Emissionsspektroskopie im UV/Vis-Bereich beobachtet
man Übergänge zwischen elektronischen Zuständen. Bei diesen Übergängen
kann sich auch der Schwingungszustand eines Moleküls ändern. Man spricht
von vibronischen (= vibratorischen + elektronischen) Übergängen. Wir gehen
davon aus, dass im Ausgangszustand nur der vibratorische Grundzustand besetzt ist.
Absorption liefert Daten über
Emission liefert Daten über
S1
S1
S0
S0
Die Intensität eines vibronischen Übergangs hängt vom Franck-Condon-Faktor
ab:
Harmonische Näherung und gleiche Kraftkonstanten in S0 und S1:
Da in einem Molekül nicht alle Moden FC-aktiv sind, liefern Absorption- und
Fluoreszenz-Spektren nur begrenzte Informationen. Zudem kommt es in
Lösung zu homogen und inhomogen Verbreiterungen.
Absorptionsspektren von Benzol
Man beobachtet eine so genannte
Schwingungsprogression mit der
Differenzfrequenz
Warum sind Linienbreiten bei vibronischen
Übergängen größer als bei reinen
Schwingungsübergängen?
Aus “Molekülphysik und Quantenchemie”
H. Haken, H.C. Wolff
IR-Spektroskopie
Unter IR-Spektroskopie versteht die Absorptionsspektroskopie im Spektralbereich des mittleren
Infraroten (ca. 400 – 3500 cm-1). Man induziert
direkt Übergänge zwischen Schwingungsniveaus
(meist bei n=0 beginnend). In der IR-Spektroskopie
wird meist Interferogramm gemessen, aus dem man
durch Fouriertransformation ein Spektrum erhält (FTIR).
Für den Extinktionskoeffizient einer IR-Bande gilt (Dipolmoment µ):
Beispiel CO2
IR-aktiv?
http://www.ir-spektroskopie.de/
Raman-Spektroskopie
Gestreute Lichtintenstität
In der Raman-Spektroskopie beobachtet das an
Molekülen inelastisch gestreute Licht.
Frequenz ω
Die Frequenz des „Primärlichtes“ liegt im NIR- bis UV-Bereich.
Die Intensität des gestreuten Lichtes ist proportional zu (Polarisierbarkeit α):
Beispiel CO2
Raman-aktiv?
Für centro-symmetrische Moleküle (nur für diese!) gilt ein Ausschlussprinzip:
IR aktiv ↔ Raman inaktiv und IR inaktiv ↔ Raman aktiv.
Polarisation liefert zusätzliche Information:
Depolarisationsverhältnis
liefert Informationen über
Symmetrie der Schwingung
(hängt von Detektionsgeometrie ab)
Was schwingt wo im Spektrum?
Ein Beispiel
OH
O
H
H
H
H
O
N
+
O
Raman/IR Atlas of Organic Compounds, B. Schrader, W. Meier, Verlag Chemie 1974
Jenseits der harmonischen Näherung:
Anharmonizitäten
Die harmonische Näherung ist der Anfangspunkt bei der Beschreibung molekularer Schwingung. Sie ist aber nicht immer der Endpunkt. Viele Phänomene
lassen sich nicht im Rahmen der harmonischen Näherung beschreiben, z.B:
Ober- und Kombinationstöne
Fermi-Resonanzen
H 20
S. Il Nam et al. Bull. Korean
Chem. Soc. 22 (2001) 989
http://www.lsbu.ac.uk/water/vibrat.html#r130
Umverteilung von Schwingungsenergie
Behandlung von Anharmonizitäten
Man entwickelt wieder das Potenzial um die Gleichgewichtslage, bricht aber
nicht nach dem zweiten Term ab:
Meist werden Terme bis zur vierten Ordnung berücksichtigt.
Für die Energien ergibt sich dann (n1, n2,.. sind die Quantenzahlen der Moden):
Xij sind die Anharmonizitätskonstanten
Xii diagonale Anharmonizität (am
Beispiel des Morse-Potenzials)
Xij außerdiagonale Anharmonizität
Besetzung der Mode j
beeinflusst die Frequenz
der Mode i.
Wichtig für der Verständnis
von Temperatur-Effekten!
Wegen der Nullpunktamplitude „sehen“ die
Kerne auch bei T= 0 K ein anharmonisches
Potenzial. Auch Nullpunktenergien werden
von Anharmonizitäten verändert.
http://www.consol.ca/downloads/MathCad/Morse.pdf
Anharmonizität und 2-Niveau-System:
Fermi-Resonanzen
IR Absorption
In einem polyatomaren Molekül kann es passieren, dass zufällig die Energie
einer fundamentalen Anregung mit der eines Obertons zusammenfällt.
Ohne Anharmonizität
Mit Anharmonizität
Frequenz ω
Diese Aufspaltung bezeichnet man als Fermiresonanz. Sie liefert direkte
Informationen über Anharmonizitäten.
Ist die Energie der fundamentalen Anregung oder des Obertons abhängig
vom Lösungsmittel, dann kann die Fermi-Resonanz durch das Lösungsmittel
„an- und abgeschaltet“ werden.
Ausblick: Anharmonizitäten und Energiefluss
Bei der Erhaltung der Normalmoden wurde die Kraftkonstanten Matrix diagonalisiert. Dies bedeutet, dass die Normalmoden von einander völlig unabhängig sind. Es findet demnach auch kein Energiefluss zwischen den
Moden statt.
Energiefluss ist demnach ein anharmonischer Effekt!
Beispiel: Energiefluss in CCl2CH2
Ingmar Hartl, Dissertation 1999
Reader