Einf¨uhrung in die theoretische Physik II Ausgewählte Aufgaben zur

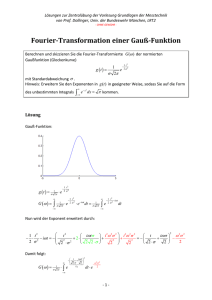
Einführung in die theoretische Physik II
Sommersemester 2015
[email protected]
Ausgewählte Aufgaben zur Klausurvorbereitung –Lösungshinweise
Aufgabe 1: Elektrostatik
Betrachten Sie eine geladene Kugel (Radius R) mit Ladungsdichte ρ(r) = ρ0 r/R.
a. Berechnen Sie mit Hilfe des Gauss’schen Satzes das elektrische Feld innerhalb und ausserhalb der Kugel.
b. Berechnen Sie das elektrostatische Potential φ(~r) unter der Annahme dass φ(∞) = 0.
c. Skizzieren Sie den Potentialverlauf.
d. Überprüfen Sie, welches der Felder
~ 1 (~r) = (2zx + y 2 )êx + 2yxêy + x2 êz
E
~ 2 (~r) = (zx + y 2 )êx + 2yxêy + xêz
E
und ein elektrostatissches Feld sein kann. Berechnen Sie für dieses die Ladungsdichte und das Potential.
a. Aus Symmetriegründen ist hat das Feld nur eine Radialkomponente,
~ r) = Er (r)êr .
E(~
(1)
Wir verwenden den Gauss’schen Satz der Elektrodynamik
Z
Z
Z
1
0
3 0 ~ ~ 0
~
d~a · E(~r ) =
d r ∇E(~r ) =
d3 r0 ρ(~r0 ).
0 Vr
∂Vr
Vr
für ein Kugel-Volumen Vr = {|~r0 | ≤ r}.
Oberflächeneintegral:
Z
~ r0 ) = 4πr2 Er (r),
d~a · E(~
∂Vr
(= Oberflächeninhalt × Betrag des Feldes, wegen der Kugel-Symmetrie.)
Volumenintegral: (Kugelkoordinaten)
1
0
Z
π
1
0
Z
4π
=
0
Z
d3 r0 ρ(~r0 ) =
Vr
Z
2π
sin(ϑ)dϑ
0
0
r0
r0
Z
2
dr0 r0 ρ(r0 )
dϕ
0
2
dr0 r0 ρ(r0 )
(2)
0
Für r < R:
1
0
Z
4πρ0
R0
Z
1
0
Z
4πρ0
d r ρ(~r ) =
R0
Vr
Z
d3 r0 ρ(~r0 ) =
Vr
r0
3
dr0 r0 =
0
πρ0 r4
R0
(3)
πρ0 R3
0
(4)
Für r ≥ R:
3 0
0
R
3
dr0 r0 =
0
Zusammensetzen ergibt
(
Er (r) =
ρ0 r 2
4R0
ρ0 R3
4r 2 0
r<R
r≥R
(5)
~ r) = −∇Φ
~ erhält man das Potential aus
b. Wegen E(~
Z
Φ(~r) − Φ(∞) =
~
d~s · E,
C
wobei C ein beliebiger Weg von ~r nach ∞ ist. Hier wählen wir einen radialen Weg.
Z ∞
Φ(~r) =
dr0 Er (r0 ).
r
Damit für r > R:
Φ(~r) =
ρ0 R 3
4r0
und für r < R:
Z
Φ(~r) =
r
R
dr0 Er (r0 ) +
Z
∞
dr0 Er (r0 ) =
R
ρ0 r 3
ρ0 R 2
ρ0 R 3
−
+
12R0
12R0
40
c. Die Skizze sollte eine monotone Funktion zeigen, bei r = R stetig, und das richtige asymptotische Verhalten
andeuten (Φ ∼ 1/r für |~r| → ∞).
~ ×E
~ = 0. Für E1 gilt
d. Das Feld kann nur dann ein elektrostatisches Feld sein, wenn ∇
~ ×E
~ 1 (~r) = 0
∇
~ ×E
~ 2 (~r) = (x − 1)êy 6= 0
∇
~ 1 (~r) ein elektrisches Feld. Die Ladungsdichte erhält man as der Maxwell Gleichung
Also ist nur E
~E
~ 1 = 2z + 2y.
ρ(~r) = 0 ∇
(6)
Potential: Wir wählen den Potentialnullpunkt bei ~r = 0. Dann gilt
Z
~
Φ(~r) =
d~s · E,
C
wobei C ein beliebiger Weg von ~r nach 0 ist. Wir wählen z.B. den Weg längs der drei Koordinatenachsen
Z x
Z y
Z z
−Φ(~r) =
dx0 Ex (x0 , 0, 0) +
dx0 Ey (x, y 0 , 0) +
dx0 Ez (x, y, z 0 )
0
0
0
(Beachte Minus vor Φ, dafür Weg von 0 nach ~r).
Φ(~r) = −y 2 − zx2 .
~ r) = −∇Φ
~ nachprüfen.)
(Kann man durch E(~
Aufgabe 2: Bildladungen
Zwei positive geladene Punktladungen befindet sich in den Punkten (0, 0, a) und (d, 0, a) oberhalb einer perfekt
leitenden Oberfläche, die durch die Ebene z = 0 gegeben ist.
a. Berechnen Sie das elektrostatische Potential der Anordnung für z > 0 mit Hilfe der Bildladungsmethode.
b. Berechnen Sie die x-Komponente der Kraft auf eine der Ladungen, d.h. die Komponente parallel zur Oberfläche und erwickeln Sie den Ausdruck für d a.
a. Das Potential für z > 0 ist die Superposition von 4 Punktladungspotentialen: +Q bei (0, 0, a), +Q bei
(d, 0, a), sowie die Bildladungen −Q bei (0, 0, −a), −Q bei (d, 0, −a) (denn diese Anordnung ergibt Φ =
const. auf der Metalloberfläche.)
1
1
Q h
p
+p
Φ(~r) =
2
2
2
2
4π0
x + y + (z − a)
(x − d) + y 2 + (z − a)2
i
1
1
−p
−p
.
(7)
(x − d)2 + y 2 + (z + a)2
x2 + y 2 + (z + a)2
b. Kraft auf Ladung bei (0, 0, a) gegeben durch Summe der Kräfte durch die anderen drei Punktladungen.
(0, 0, −a) übt nur Kraft in z-Richtung aus; Summe der Coulombkräfte der Ladungen +Q bei (d, 0, a) und
−Q bei (d, 0, −a):
i
d
Q2 h
1
(8)
Fx =
− 2+p
3
4π0
d
d2 + (2a)2
Entwicklung für d a:
Fx =
i
Q2 h
1
−
1
+
p
3
4π0 d2
1 + (2a/d)2
Taylor-Entwicklung (1 + )α = 1 + α + O(2 ) für α = 3/2 und = (2a/d)2 ergibt
i
Q2 h 6a2
4
Fx =
−
+
O((a/d)
)
4π0 d2
d2
(9)
(10)
Aufgabe 3: Magnetostatik
Betrachten Sie einen langen Draht mit Radius R entlang der z-Achse. Die Stromdichte innerhalb des Drahtes sei
durch
~j(~r) = êz j0 [1 − (s/R)2 ]
p
gegeben, wobei s = x2 + y 2 den Abstand von der z-Achse bezeichnet.
~ r) innerhalb und ausserhalb des Drahtes.
a. Bestimmen Sie das magnetische Feld B(~
b. Berechnen Sie die Kraft auf eine stromdurchflossene rechteckige Leiterschleife C, bestimmt durch die Eckpunkte (a, 0, 0) → (a, 0, b) → (a0 , 0, b) → (a0 , 0, 0) → (a, 0, 0).
c. Aus Symmetriegründen können sie folgern, dass das Vektorpotential der Anordnung in êz -Richtung zeigt
~ r) ausserhalb des Drahtes, indem Sie den Satz von Stokes mit der
und nur von s abhängt. Bestimmen Sie A(~
~
~
~
~ so dass A
~ = 0 für
Beziehung ∇ × A = B auf eine Kurve C wie in Aufgabe b anwenden. Wählen Sie A
s = R.
~ r) = y 2 êx + 2yzêy − 3zxêz ?
d. Kann es sich bei dem folgenden Feld um ein Magnetfeld handeln: B(~
~ r) = êϕ Bϕ (s).
a. Wir verwenden Zylinderkoordinaten (s, ϕ, z). Aus der Symmetrie der Anordnung folgt B(~
0
0
Wir verwenden das Ampere’sche Durchflutungsgesetz für eine Kreisfläche Sr = {s : s < s} in der Ebene
z = 0.
Z
Z
Z
~ × B(~
~ r0 ) =
~ r0 ).
µ0
d~a · ~j(~r0 ) =
d~a · ∇
d~s · B(~
Ss
Ss
∂Ss
Wegen der Zylindersymmetrie ergibt das Linienintegral (Im Gegenuhrzeigersinn um z wenn die Fläche in
+z Richtung orientiert ist)
Z
~ r0 ) = 2πsBϕ (s).
d~s · B(~
∂Ss
Das Flächenintegral ergibt
Z
d~a · ~j(~r0 ) = µ0
µ0
Ss
Für s < R erhält man
Z
s
ds0 2πs0 jz (s0 )
0
h s2
s4 i
d~a · ~j(~r0 ) = 2πµ0 j0
−
,
2
4R2
Ss
Z
µ0
für s > R
Z
d~a · ~j(~r0 ) = 2πµ0 j0
µ0
Ss
R2
4
Für das Magnetfeld erhält man demnach
(
Bϕ (s) =
µ0 j0
h
s
s2
2 − 4R2
µ0 j0 R2
4s
i
,
s<R
s>R
(11)
b. Allgemein gilt für die Kraft auf eine stromdurchflossene Leiterschleife C,
Z
~
~
F =I
d~l × B.
C
Aus Symmetriegründen heben sich die Kräfte auf die Drahtabschnitte (a, 0, b) → (a0 , 0, b) und (a0 , 0, 0) →
(a, 0, 0) weg. Längs der anderen Abschnitte ist das Feld jeweils konstant. Wir erhalten
F~ = Ibêz × êϕ Bϕ (a) + Ib(−êz ) × êϕ Bϕ (a0 ) = ês Ib[Bϕ (a0 ) − Bϕ (a)]
mit dem Ergebnis von a.
c. Verwende der Satz von Stokes für eine Fläche S die von der Kurve ∂S = (R, 0, 0) → (R, 0, b) →
(s, 0, b) → (s, 0, 0) → (R, 0, 0) umschlossen wird:
Z
Z
~ × A(~
~ r0 ) =
~ r0 ).
d~a · ∇
d~s · A(~
S
∂S
~ ×A
~=B
~ und der Symmetre von B
~ erhält man die linke Seite als
Wegen ∇
Z
Z s
Z s
bµ0 j0 R2
µ0 j0 R2
~ × A(~
~ r0 ) = b
=
log(s/R).
d~a · ∇
ds0 B(s0 ). = b
ds0
0
4s
4
S
R
R
Zur Kurvenintegral trägt nur der Abschnitt (s, 0, b) → (s, 0, 0) bei (da A = 0 bei R = 0), und damit
Z
~ r0 ) = −bAz (s).
d~s · A(~
∂S
Damit gilt
Az (s) =
µ0 j0 R2
log(R/s).
4
d. Das gegebene Feld kann kein Magnetfeld sein, denn
~ ·B
~ = 2z − 3x 6= 0.
∇
(12)
Aufgabe 4: Maxwell-Gleichungen
a. Betrachten Sie die Überlagerung von zwei ebenen Wellen mit Ausbreitungsrichtung in z-Richtung, von
denen eine in êx und eine in êy -Richtung polarisiert ist. Die Feldamplituden sei E1 und E2 , und die Wellen
seien um π/2 phasenverschoben. (Es handelt sich um eine elliptisch polarisierte Welle). Geben Sie für beide
Anteile der Welle die explizite Form des elektrischen und magnetischen Feldes an.
b. Berechnen Sie die zeitgemittelte Energiestromdichte (Poynting-Vektor).
a. Wir verwenden als Ansatz einer ebenen Welle den Realteil von
~ r, t) = E
~ 0 ei~k~r−iωt , B(~
~ r, t) = B
~ 0 ei~k~r−iωt ,
E(~
~ 0 = 1 ~k × E
~ 0 . (Die zweite Beziehung folgt aus der Maxwell Gleichung ∇×
~ E
~ = − ∂ B,
~
mit |k| = ω/c und B
ck
∂t
angewendet auf ebene Wellen.) Im Beispiel gilt ~k = kêz , so dass die Superposition der zwei Wellen gegeben
ist durch
~ r, t) = E1 êx eikz−iωt + E2 êy eikz−iωt+π/2 , B(~
~ r, t) = E1 êy eikz−iωt − E2 êx eikz−iωt+π/2 .
E(~
c
c
b. Poynting Vektor (verwende reelle Felder(!))
~=1E
~ ×B
~
S
µ0
1 =
E1 êx cos(ikz − iωt) + E2 êy cos(ikz − iωt + π/2)
µ0 c
× [E1 êy cos(ikz − iωt) − E2 êx cos(ikz − iωt + π/2)].
(13)
(14)
Unter dem Kreuzprodukt fallen in diesem Fall die Interferenzterme ∝ E1 E2 weg, es bleibt
~ = 1 E12 êz cos(ikz − iωt)2 + E22 êz cos(ikz − iωt + π/2)2 .
S
µ0 c
(15)
Mittelung der cos2 Terme über eine Schwingungsperiode ergibt
~ = 1 1 E12 + 1 E22 êz .
S
µ0 c 2
2
(16)
Aufgabe 5: Fourier-Transformation Betrachten Sie den Fourier-Ansatz
Z
h
i
dk v+ (k)eikx−iωt + v− (k)eikx+iωt .
v(x, t) =
(17)
für eine eindimensionale Welle. Zur Zeit t = 0 sei die Welle gegeben durch v(x, 0) = Θ(1 − |x|), und ihre
Zeitableitung durch v̇(x, 0) = 0.
a. Berechnen Sie die Fouriertransformierten von v(x, 0) und v̇(x, 0).
b. Bestimmen Sie v± (k) durch Vergleich des Ergebnisses von a mit der Fouriertransformierten von Gl. (17).
a. Bestimmung der Fouriertransformierten aus der gegebenen Anfangsbedingung:
1
2π
Z
∞
dxv(x, 0)e
−ikx
−∞
1
=
2π
∞
Z
−ikx
dxΘ(1 − |x|)e
−∞
1
2π
Z
1
=
2π
Z
1
dxe−ikx =
−1
1 e−ik − eik
1 sin(k)
=
2π
−ik
π k
∞
dxv̇(x, 0)e−ikx = 0
−∞
b. Bestimmung der Fouriertransformierten aus Gl. (17): Mit
Z
h
i
0
0
v(x, 0) = dk 0 v+ (k 0 )eik x + v− (k 0 )eik x .
folgt
1
2π
Z
∞
dxv(x, 0)e−ikx
−∞
Z ∞
Z
h
i
0
0
1
=
dx dk 0 v+ (k 0 )eik x e−ikx + v− (k 0 )eik x e−ikx
2π −∞
Z
Z ∞
Z ∞
h
i
0
0
1
1
= dk 0 v+ (k 0 )
dxeik x e−ikx + v− (k 0 )
dxeik x e−ikx
2π −∞
2π −∞
R
Mit Verwendung von dxeikx = 2πδ(k) folgt
Z ∞
1
dxv(x, 0)e−ikx = v+ (k) + v− (k)
2π −∞
Analog ergibt
Z
v̇(x, 0) =
1
2π
Z
h
i
0
0
dk 0 − iωv+ (k 0 )eik x + iωv− (k 0 )eik x .
∞
dxv̇(x, 0)e−ikx = iω[−v+ (k) + v− (k)].
−∞
Vergleich mit a ergibt
v+ (k) = v− (k) =
1 sin(k)
.
2π k
(18)
(19)
(20)