Heft 17 - mpg

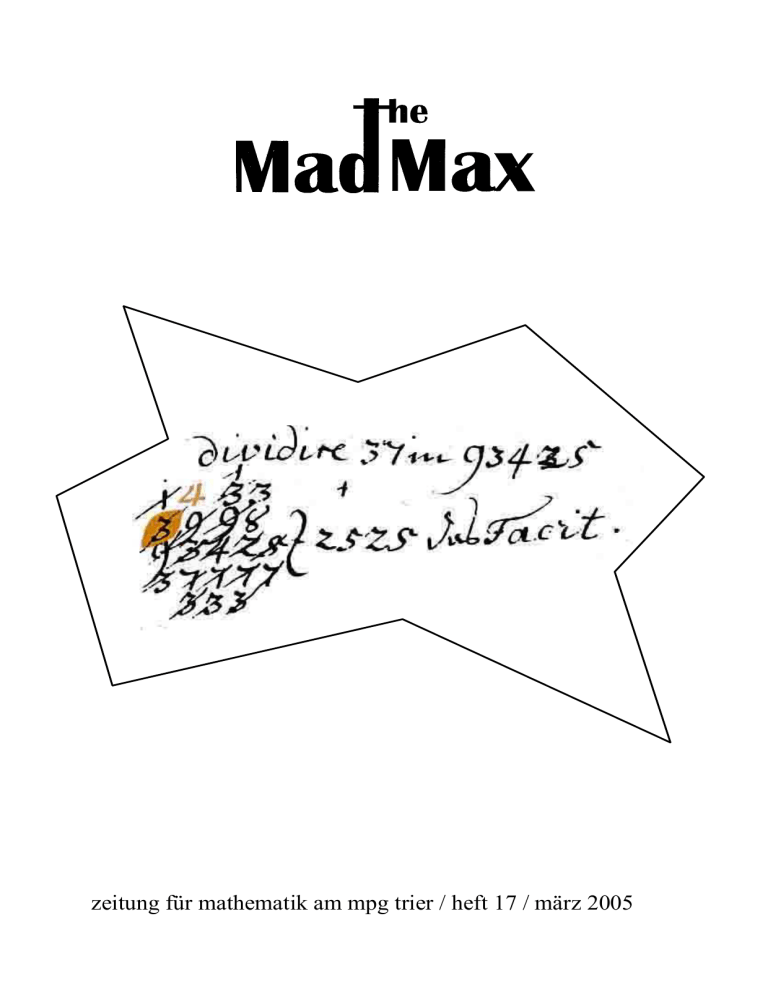
zeitung für mathematik am mpg trier / heft 17 / märz 2005
Hallo liebe MadMax – Freunde,
unser Heft erscheint etwas später als gewohnt, aber wir
waren noch zu sehr mit der Fertigstellung unserer
Arbeiten für den Wettbewerb „Jugend Forscht“
beschäftigt. Weil in jeder Gruppe mindestens ein
Mitglied 15 oder älter war, mussten wir uns diesmal mit
den Schülern der Oberstufe messen. Umso erfreulicher
der zweite Preis von Esther Bischoff, Tobias Dietz und
Jan
Peter
Wagner
mit
ihrer
Arbeit
zum
„Sekretärinnenproblem“, die ihr auch in dieser Ausgabe
nachlesen könnt.
Seite
28 Plastikplättchen
von Sebastian Bollig und Klaus Wollscheid
Das Problem der besten Wahl
von Esther Bischoff, Tobias Dietz, und Jan Peter
Wagner
4
6
Schnell- und Langsamgeher
von Simon Reinsch
13
Eine andere Art zu Dividieren
von Sebastian Bollig und Klaus Wollscheid
17
Streichen von Lattenzäunen
Von Lucas Heise Mogan Ramesh und Alexander
Resch
Wurzelziehen für Nichtmathematiker
von Jean-Philippe Merz
Das (3n+1) - Problem
von Jean-Philippe Merz und Gereon Lex
2
20
26
27
Die Aufgabe
Ein Junge hat 28 Plastikplättchen, auf denen jeweils
eine Ziffer steht, aneinandergereiht, so dass eine
28stellige Zahl entstanden ist. Der Vater entfernt aus der
Ziffernreihe 10 Plättchen, und zwar eine Null, eine Eins,
eine Zwei, eine Drei, eine Vier, eine Fünf, eine Sechs,
eine Sieben, eine Acht und eine Neun. Zurück bleibt
folgende lückenhafte Zahl:
5_383_8_2_936_5_8_203_9_3_76
Darauf der Vater zu seinem Sohn: "Wenn ich die zehn
Ziffern in einer zufälligen Reihenfolge wieder in die
Lücken dieser Zahl setze, wie groß ist dann die
Wahrscheinlichkeit in Prozent, dass die Zahl durch 396
teilbar ist?"
Die Lösung
Man zerlegt 396 in ihre Primfaktoren (2²,3²,11) und testet
welche Ziffern man bei
5_383_8_2_936_5_8_203_9_3_76
an bestimmte Stellen einsetzen muss, damit die Zahl
durch 396 teilbar ist. An der Primfaktorzerlegung sieht
man, dass die Zahl durch 4, 9, 11 teilbar sein muss.
Dazu überprüft man zuerst die Zahl auf Teilbarkeit durch
vier.
3
Regel: Wenn die letzten zwei Stellen einer Zahl durch 4
teilbar ist, ist auch die Zahl durch 4 teilbar.
Also: 76:4=19
Folge:
Die Zahl ist durch 4 teilbar, egal wie die restlichen Ziffern
auf die Zahl verteilt werden.
Danach überprüft man die Zahl auf Teilbarkeit durch
neun.
Regel: Wenn die Quersumme einer Zahl durch 9 teilbar
ist, ist auch die Zahl durch 9 teilbar.
Also:
(5+3+8+3+8+2+9+3+6+5+8+2+0+3+9+3+7+6)+(0+1+2+
3+4+5+6+7+8+9)=135. Es ist 135:9=15
Folge:
Die Zahl ist durch 9 teilbar, egal wie die restlichen Ziffern
auf die Zahl verteilt werden.
Jetzt muss nur noch die Teilbarkeit auf 11 überprüft
werden.
Regel: Wenn man die Summe aller Zahlen an geraden
Stellen von der Summe aller Zahlen an ungeraden
Stellen abzieht und die Differenz durch 11 teilbar ist, ist
auch die Zahl durch 11 teilbar.
Für die ungeraden Stellen erhält man die Summe
5+3+3+8+2+9+6+5+8+2+3+9+3+7=73. Dies kann man
berechnen, weil alle ungeraden Stellen besetzt sind. In
4
der Zahl sind aber nur vier gerade Stellen besetzt, aber
das ist kein Problem, weil an den restlichen Stellen alle
Ziffern von 0 bis 9 genau einmal eingesetzt werden.
Also: 8+3+0+6+0+1+2+3+4+5+6+7+8+9=62
Differenz: 73-62=11
Folge:
Die Zahl ist also durch 11 teilbar, ohne dass man weiß,
wo die einzelnen Ziffern genau sitzen..
Das Ergebnis:
Man kann die einzusetzenden Zahl einsetzen wie man
will. Also ist die Zahl zu 100% durch 396 teilbar.
Theoretisch könnte man alle Zahlen beliebig tauschen,
solange alle Ziffern die an ungeraden Stellen stehen an
ungeraden Stellen bleiben und alle Ziffern die an
geraden Stellen stehen an geraden Stellen bleiben.
Außerdem muss hinten immer 76 oder eine andere
durch vier teilbare, zweiziffrige Zahl stehen bleiben
(wegen der Teilbarkeit durch 4).
Inzwischen haben wir die Fragestellung erweitert und
sind ein paar neuen Erkenntnissen auf der Spur.
Darüber könnt ihr dann im nächsten Heft lesen.
5
Das Problem der besten Wahl
1.Worum geht’s?
Ein Chef ist auf der Suche nach einer neuen Sekretärin.
Er hat 10 Damen zu einem Vorstellungsgespräch
eingeladen, die sich ihm nacheinender vorstellen. Der
Chef muss jedoch direkt nach dem Gespräch mit einer
Dame entscheiden, ob er sie einstellt oder nicht. Er hat
keine Möglichkeit seine Entscheidung rückgängig zu
machen. Wie muss er vorgehen, um die größte
Wahrscheinlichkeit zu haben, die beste unter ihnen zu
finden?
2. Das Grundprinzip:
Um entscheiden zu können, wer die beste ist, braucht
der Chef Vergleichsmöglichkeiten. Deshalb muss er eine
bestimmte Anzahl der ersten Damen auf jeden Fall
abweisen, um die anderen mit ihnen vergleichen zu
können. Nach dieser Erkundungsphase (EP) nimmt er
die erste Sekretärin, die besser ist als die qualifizierteste
der Damen in der Erkundungsphase.
3. Wie lang muss die Erkundungsphase sein, um die
größte Wahrscheinlichkeit zu haben, die beste
Sekretärin einzustellen?
Dies ist natürlich nicht leicht zu beantworten. Wenn sich
der Chef zu viele Damen „anguckt“ geht er das Risiko
ein, dass die beste bereits unter diesen ist, sodass er sie
abweist. Wenn er sich allerdings zu wenig Damen
„anguckt“ ist die Wahrscheinlichkeit hoch, dass unter
6
diesen nur wenige qualifizierte Bewerberinnen sind,
sodass kurz nach der Erkundungsphase eine Dame
besser ist als die von zuvor, aber trotzdem im Vergleich
zu vielen anderen weniger qualifiziert ist.
Es geht also darum, einen richtigen Mittelweg zu finden,
um die Wahrscheinlichkeit beider Fälle möglichst gering
zu halten.
Erster Ansatz:
Zuerst haben wir das Problem so klein wie möglich
gehalten und sind dazu von drei Bewerberinnen
ausgegangen. Voraussetzung dafür, dass man die beste
Sekretärin bekommt ist, dass sie nicht in der
Erkundungsphase ist. Die Wahrscheinlichkeit, dass
jemand in der Erkundungsphase (EP) beträgt EP/n ,
wobei n die Anzahl aller Bewerberinnen beträgt. Dass
jemand also außerhalb der EP ist, tritt mit einer
Wahrscheinlichkeit von (n-EP)/n ein.
1. Voraussetzung: Die beste Sekretärin ist nicht in
der EP
Wahrscheinlichkeit: (n-EP)/n
Des weiteren muss entweder die zweitbeste Sekretärin
in der EP sein, denn dann kann nur die beste
angenommen werden, oder die drittbeste Sekretärin
muss in der EP sein und außerhalb der EP muss die
beste vor der zweitbesten kommen.
Also:
2. Voraussetzung:
a) : Die zweitbeste Sekretärin ist in der EP.
Wahrscheinlichkeit: EP / n
7
b) : Die drittbeste Sekretärin ist in der EP und die beste
Sekretärin kommt vor der zweitbesten.
Wahrscheinlichkeit: EP / n * ½
zu a) Die zweitbeste Sekretärin ist in der EP – es
werden keine weiteren Voraussetzungen benötigt
zu b) Die drittbeste Sekretärin ist in der EP – dann muss
die beste Sekretärin vor der zweitbesten kommen, was
eine Wahrscheinlichkeit von 50% hat, also muss noch
durch 2 geteilt werden.
Es gibt also zwei Wege um zur Wahl der besten
Sekretärin zu finden:
1. (n-EP) / n * EP / n
Dies stimmt aber noch nicht so ganz, da nach dem
Eintreffen der 1. Voraussetzung (Beste ist nicht in EP),
sich die Gesamtzahl der Sekretärinnen, die für den
nächsten Fall in Frage kämen um 1 verringert, deshalb:
(n-EP) / n * EP / (n – 1)
Wenn man hier als Beispiel die EP auf 1 setzt, d.h. sich
genau eine Sekretärin anguckt und ablehnt und danach
die beste nimmt, erhält man folgenden Term:
(3 – 1) / 3 * 1 / (3 – 1)
= 2/3*1/2
=1/3
8
Dieses Ergebnis lässt sich im Kopf leicht überprüfen: Die
Wahrscheinlichkeit, dass eine bestimmte von dreien
nicht in der EP ist beträgt 2/3 und dass eine bestimmte
von den zwei verbleibenden in der EP ist beträgt ½.
Dass diese beiden Fälle gleichzeitig eintreffen hat eine
Wahrscheinlichkeit von 1/3. (Vgl. Rechnung)
Jetzt gibt es aber noch den zweiten Weg:
Die drittbeste Sekretärin ist in der EP und die beste
kommt außerhalb der EP vor der zweitbesten. Dann
sieht der Term folgendermaßen aus:
(n-EP) / n * EP / (n-1) * ½
Beispiel: (n=3; EP=1)
(3-1) / 3 * 1 / (3-1) * ½
= 2/3 * ½ * ½
= 1/6
Dies sind die beiden Wege die dazu führen, dass der
Chef die beste
Sekretärin
einstellt.
Insgesamt
beträgt
die
Wahrscheinlichkeit also Weg 1 + Weg 2, sprich:
(n-EP) / n * EP / (n – 1) + (n-EP) / n * EP / (n-1) * ½
In unserem Beispiel wäre das:
1/3 +1/6=1/2
9
Der Chef hat also eine Chance von 50%, die beste
Sekretärin zu finden, wenn er dieses Verfahren
anwendet.
Wenn er im Vergleich dazu das Zufallsprinzip
verwenden würde, würde die Wahrscheinlichkeit nur
ungefähr 33% betragen.
Wie muss man vorgehen, wenn man sich auch mit
der zweitbesten Sekretärin zufrieden gibt?
Nun haben wir uns überlegt wie stark die
Wahrscheinlichkeit steigt, wenn man sich auch mit der
zweitbesten Sekretärin zufrieden gibt und ob man die EP
verändern muss, um ein optimales Ergebnis zu erzielen.
Hierzu haben wir mit einem
angefangen, mit n = 5; EP = 1:
einfachen
Beispiel
Es bestehen folgende EP-Konstellations-Möglichkeiten:
Wer ist in Wahrscheinlichkeit WahrscheinEP?
der Entstehung
lichkeit, dass
dieser
diese
Konstellation
Konstellation
zum Erfolg
führt
1
20%
0%
(Beste)
2
20%
100%
3
20%
100%
4
20%
67%
5
20%
50%
(Schlechteste)
10
Gesamtwahrscheinlichkeit
0%
20%
20%
13%
10%
Erklärung der Tabelle:
Da es fünf mögliche Konstellationen gibt, beträgt die
Wahrscheinlichkeit für die Entstehung jeder einzelnen
ein Fünftel (= 20%).
Wenn die Beste in der EP ist, kann keine andere
Sekretärin eingestellt werden, da keine bessere mehr
kommt. Die Erfolgswahrscheinlichkeit beträgt deshalb
0%.
Wenn die Zweitbeste in der EP ist, kann nur die Beste
genommen werden und wenn die Drittbeste in der EP
ist, wird eine der beiden Besten eingestellt. Darum
beträgt die Erfolgswahrscheinlichkeit 100%.
In dem Fall, dass die Viertbeste in der EP ist, könnten
die drei besten Sekretärinnen den Job bekommen,
wodurch die Wahrscheinlichkeit, dass die erst- oder
zweitbeste außerhalb der EP vor der drittbesten
kommen nur noch 2/3 beträgt.
Falls der fünfte Fall eintritt, stehen vier Sekretärinnen zur
Wahl. Folglich wird eine der beiden Besten nur noch in
zwei von vier Fällen genommen, was 50% entspricht.
Die Gesamtwahrscheinlichkeit berechnet sich durch das
Multiplizieren der beiden ersten Wahrscheinlichkeiten
und gibt so die Wahrscheinlichkeit des Eintreffens der
ersten beiden Wahrscheinlichkeiten an.
Um nun die endgültige Wahrscheinlichkeit zu
bestimmen, mit der man mit diesem Verfahren eine der
beiden besten Sekretärinnen bekommt muss man die
Gesamtwahrscheinlichkeiten addieren, in diesem Fall
wäre dies entsprechend 63%.
11
Nun haben wir die EP auf zwei erhöht. Das Ergebnis
sieht folgendermaßen aus:
Wer
ist
in
EP?
1; 2
1; 3
1; 4
1; 5
2; 3
2; 4
2; 5
3; 4
3; 5
4; 5
Wahrscheinlichkeit
der
Entstehung
dieser
Konstellation
10%
10%
10%
10%
10%
10%
10%
10%
10%
10%
Wahrscheinlichkeit,
dass
diese
Konstellation zum
Erfolg führt
0%
0%
0%
0%
100%
100%
100%
100%
100%
67%
Die endgültige Wahrscheinlichkeit,
Verfahren zum Erfolg führt: 56,7%
Gesamtwahrscheinlichkeit
0%
0%
0%
0%
10%
10%
10%
10%
10%
6,7%
dass
dieses
Hier sieht man, dass bei n = 5 es besser ist die EP auf
eins zu setzen und nicht wie zuvor bei ungefähr 36%
anzulegen.
12
Schnell- und Langsamgeher
Wenn man in einer Stadt in ein Geschäft geht, kann man
während man auf den Verkäufer wartet gut aus dem
Schaufenster gucken. Um die Wartezeit zu verkürzen
kann man Personen zählen. Dabei fällt auf, dass einige
Leute schnell und einige langsam gehen. Wenn man
diese zählt, kommt man bei 100 Passanten z.B. auf 25
“Schnellgeher“ und 75 “Langsamgeher“. Aber was sagt
diese Zahl aus? Wohnen in der Stadt tatsächlich 25%
“Schnellgeher“ und 75% “Langsamgeher“? Die
Personen können ja auch in der Messzeit nicht
angekommen sein, was eher für die Langsamgeher gilt.
Dazu suchen wir jetzt mit Hilfe eines einfachen
mathematischen Modells eine Lösung.
Das Kreismodell
Unsere Modellstadt soll nur eine ringförmige Straße
haben. Darauf laufen z.B. 5 Schnellgeher und 10
Langsamgeher im Kreis.
Schnellgeher
Langsamgeher
Zähler
13
Wenn in dieser Stadt die Schnellgeher doppelt so
schnell gehen wie die Langsamgeher, und wir solange
zählen, bis alle Schnellgeher vorbeigekommen sind,
dann zählen wir 5 Langsamgeher und 5 Schnellgeher.
Also könnte man vermuten, dass in der Stadt 50%
Langsamgeher und 50%Schnellgeher wohnen. Dabei
wissen wir ja, dass in Wahrheit 5 Schnellgeher und 10
Langsamgeher in der Stadt waren (33%Schnellgeher
und 66%Langsamgeher).
Mit anderen Worten:
Wir zählen Langsamgeher und Schnellgeher. In Wahrheit haben wir nur die Hälfte der Langsamgeher, aber
alle Schnellgeher gezählt und deshalb einen falschen
Schluss gezogen.
Gibt es nun eine Möglichkeit direkt das wahre Ergebnis
zu finden(ohne alle Passanten anzumalen oder so...)?
Für die allgemeine Lösung dieser Frage machen wir
unser Modell noch einfacher.
Das „Einbahnstadtmodell“
Zähler
Angenommen wir zählen L Langsamgeher und S
Schnellgeher, dann könnte man vermuten, dass in der
14
L
S
⋅100 % Langsamgeher und
⋅100 %
L+S
L+S
Schnellgeher wohnen. Wie viele Schnell- und Langsamgeher wirklich in der Stadt wohnen, hängt aber davon
ab, wie stark sich die Geschwindigkeiten unterscheiden.
Stadt
Zusammenfassung:
Ausgangsposition:
- Es gibt S (Schnellgeher) und L (Langsamgeher)
- Die Geschwindigkeit der Schnellgeher vS entspricht
dem doppelten(oder dem x-fachen) der
Geschwindigkeit der Langsamgeher vL bzw. die
Geschwindigkeit der Langsamgeher ist halb so groß
1
(oder so groß) wie die der Schnellgeher
x
- die Schnell- und Langsamgeher sind gleichmäßig in
der Stadt verteilt
- es gibt eine zufällige Stelle in der Stadt, an der die
Passanten gezählt werden
- beobachtet wird bis alle Schnellgeher am Zählpunkt
vorbeigekommen sind.
Ergebnis:
Es wurde nur die Hälfte(oder
1
) der Langsamgeher
x
beobachtet.
Schlussfolgerung:
15
Der Anteil s der von uns gezählten Schnellgeher ist
gleich der Anzahl der Schnellgeher geteilt durch ein x-tel
der Langsamgeher plus die Anzahl der Schnellgeher ist:
S
s=
1
L+S
x
Nach dem selben Prinzip ermitteln wir auch den Anteil l
der gezählten Langsamgeher:
1
L
x
l=
1
L+S
x
z.B.: S = L = 50 und x = 2
50 2
= ≈ 67%
75 3
25 1
→l =
= ≈ 33%
75 3
→s=
Erwartungsgemäß erhalten wir unterschiedliche Prozentsätze. Umgekehrt können wir das Verhältnis S/L
berechnen, wenn wir z.B. s = 90% = 0,9 kennen und x
z.B. 4 ist:
S
0,9 = 1
4 L+S
Dann erhält man S = 2,25 L, d.h. in der Stadt wohnen
nicht etwa 90% Schnellgeher, sondern nur knapp 70%.
16
Hier wird ein Teilungsverfahren aus einem alten
Mathematikbuch von Georg Ludwig Lich aus dem Jahre
1776 erklärt. Dieses Verfahren haben wir in einzelnen
Schritten untersucht.
1. Dividieren durch Zahlen von 1-9:
Erklärung:
Lichs Verfahren:
3
7896
4
1
32
7896
44
19
Heutiges Verfahren:
7896: 4=1974
4
38
36
29
28
16
16
0
17
321
7896
444
197
321
7896
4444
1974
Wie man sieht, teilt Lich anders als wir heute. Er schreibt
den Divisor zuerst unter die erste Ziffer. Dann dividiert er
die darüber stehende Zahl. Das Ergebnis schreibt er
rechts neben den Ergebnisstrich, den Rest über den
Dividend. Nun wiederholt er dies mit der zweiten, dritten
und vierten Ziffer.
2. Dividieren durch eine Zahl mit mehr als einer Stelle:
Erklärung (nach Lichs Verfahren):
Zuerst schreibt er die zu
14
dividierende Zahl (in diesem Fall
39
93425) in eine Reihe und
93425 2
schreibt unter die ersten zwei
37
Ziffern (9,3) die Zahl durch die
dividiert wird (37) und führt die Division durch. Das
Ergebnis schreibt er immer neben den Ergebnisstrich.
18
Für die grau hinterlegten Zahlen haben wir keine
Erklärung.
1
3
9
3
Nun streicht Lich die bereits
verwendeten Zahlen durch und
schreibt den Rest über die
25
Ziffern (1 über die graue 3, 9
über 3), danach die erste Ziffer
der Zahl, durch die dividiert
werden soll, unter die letzte Ziffer der ersten Zahl (3
unter 7) und die letzte Ziffer der Zweiten Zahl rechts
neben die zweite Ziffer der ersten Zahl (7 rechts neben
7). Dies führt er jetzt weiter bis er die letzte Ziffer (5)
dividiert hat und nun kann man hinter dem
Ergebnisstrich
die
Lösung
erkennen
(2525).
1
3
9
3
4
9
3
7
3
4
9
3
7
3
3
9
425
7
1
3
9
4
7
3
3
8
25
7
252
1
3
9
3
4
9
3
7
3
1
3
9
4
7
3
3
8
25
77
3
2525
Wer eine Idee für die grau unterlegten Zahlen hat kann
uns diese gerne mitteilen.
Witz:
Frage:
Wie oft kann man 7 von 83 abziehen, und was
bleibt am Ende übrig?
Antwort: Man kann so oft wie man will 7 von 83
abziehen, und es bleibt jedes mal 76 über.
19
Streichen von Lattenzäunen
1. Das Problem
Ein Mann streicht einen Lattenzaun mit genau 100
Latten rot. So recht zufrieden ist er damit jedoch nicht zu gleichförmig scheinen ihm die Latten gestrichen. Also
kehrt er zum Anfang des Lattenzauns zurück, geht
erneut los und streicht jede 2. Latte blau.
Einmal in
Fahrt gekommen, ist der Mann nicht mehr zu bremsen.
Immer wieder marschiert er den Lattenzaun entlang und
streicht jede 3., 4., 5.,....Latte um. Stets wird eine rotdurch eine blaugestrichene Latte ersetzt und umgekehrt,
bis schließlich nur die 100. Latte noch einmal die Farbe
wechselt. Wie viele Latten sind nun rot – und welche?
2. Die Lösung
In einer Tabelle haben wir einen Lattenzaun simuliert.
Mit Hilfe dieser Tabelle kann man nach jedem einzelnen
Durchgang erkennen welche Latten rot, welche blau sind
(Tabelle im Anhang; rot und blau sind nur als
verschiedene
Grauschattierungen
dargestellt).
Aber
daraus war zuerst kein Schema zu erkennen. Schließlich
20
ist uns aufgefallen, dass die mit einer Quadratzahl
nummerierten Latten als einzige rot bleiben.
Wir kamen auf die Idee, dass dies mit der Anzahl der
Teiler der Quadratzahlen zu tun haben muss. Denn bei
jedem Teiler der Zahl wird die Latte ja umgestrichen. Wir
fanden heraus, dass Quadratzahlen als einzige eine
gerade Anzahl an Teilern haben. Dabei wird die 1 nicht
21
dazugezählt, da am Anfang alle Latten sowieso rot
gestrichen werden. Zahlen die keine Quadratzahlen
sind, haben immer eine ungerade Anzahl an Teilern und
werden deswegen blau.
Ein Beispiel:
36 ist eine Quadratzahl und hat 6 von 1 verschiedene
Teiler
2,
3,
4,
6,
9,
12, 18,
36
24 ist keine Quadratzahl und hat 7 von 1 verschiedene
Teiler
2, 3, 4, 6, 8, 12, 24
Die 24. Latte ist am Anfang rot und wird dann wegen der
Teiler 2 und 3 blau und wieder rot gestrichen. Das
22
wiederholt sich für die Teiler 4,6 und 8,12. Dann bleibt
noch 24 selbst als Teiler übrig und die Latte bleibt blau.
Dass Zahlen, die keine Quadratzahl sind, eine ungerade
Anzahl an Teilern haben, liegt daran, dass Teiler einer
Zahl immer mit einem Partner auftauchen (siehe Pfeile
in den Zeichnungen; das Produkt der beiden Partner ist
die Zahl selbst). Die Zahl selber hat den Partner 1 und
dadurch, dass diese nicht dazugezählt wird, ist die Zahl
selber
immer
ohne
Partner.
Dies
gilt
nicht
bei
Quadratzahlen, da diese außer der Zahl selber eine
zweite Zahl ohne Partner haben, nämlich die Wurzel (sie
ist praktisch ihr eigener Partner, z.B.: 6 * 6 = 36).
3. Erweiterung des Problems
Nach diesen Erkenntnissen haben wir überlegt wie es
ist, wenn man nur jede 2, 4, 6, 8, 10, ..... Latte streicht.
Dabei kamen wir auf das Ergebnis, dass ungerade
Zahlen bei dieser Vorgehensweise gar nicht verändert
werden, da diese keine geraden Teiler haben. Gerade
23
Zahlen werden auch nicht verändert da diese immer
eine gerade Anzahl an geraden Teilern haben. Nur
Zahlen die nach Division durch 2 eine Quadratzahl
ergeben haben eine ungerade Anzahl an Teilern und
werden so auch verändert.
T12 = {1, 2, 3, 4, 6,
12}
Gerade Anzahl an geraden Teilern: färbt sich nicht
T21 = {1, 3, 7, 21}
Nur ungerade Teiler: färbt sich nicht
T18 = { 1, 2, 3, 6, 9, 18}
Ungerade Anzahl an geraden
Teilern: färbt sich
= 2x9 (Vielfaches einer Quadratzahl)
24
Bei diesem Problem muss man zwischen dem 2-fachen
einer geraden Quadratzahl und dem 2-fachen einer
ungeraden Quadratzahl unterscheiden.
2-faches einer geraden Quadratzahl:
Eine gerade Quadratzahl hat eine gerade Anzahl an
geraden Teilern, wird also nicht verändert. Bei der
Verdopplung der Zahl kommt als Teiler nur das 2-fache
der Quadratzahl hinzu. D.h., die neue Zahl hat eine
ungerade Anzahl an geraden Teilern, woraus folgt, dass
sie verändert wird.
2-faches einer ungeraden Quadratzahl:
Eine ungerade Quadratzahl hat 3 ungerade Teiler,
weswegen sich diese nicht verändert. Das 2-fache
dieser
ungeraden
Quadratzahl
übernimmt
die
3
ungeraden Teiler und jeweils das Doppelte eines dieser
Teiler, woraus folgt, dass es eine ungerade Anzahl an
geraden Teilern hat. Nämlich 3 ungerade und 3 gerade
Teiler, wobei die ungeraden keine Rolle spielen, da nur
gerade Zahlen verändert wurden.
25
Wurzelziehen für Nichtmathematiker
Dieser Satz begeistert jeden Nichtmathematiker: “Unter
der Quadratwurzel einer nicht-negativen Zahl x aus dem
Körper der reellen Zahlen versteht man in der
Mathematik diejenige positive Zahl r, deren Quadrat r2
gleich x ist. Kurz: r = x !“
Aber halb so schwer: Es ist
49 = 7 , weil 7² = 49 ist.
Das Symbol
für die Quadratwurzel wurde übrigens
zum erstenmal während des 16. Jahrhunderts benutzt.
Es wird vermutet, dass das Zeichen eine modifizierte
Form des kleinen r ist, das als Abkürzung für das
lateinische Wort "radix" (Wurzel) steht.
Soweit so gut. Aber wie berechnet man Wurzeln, wenn
unter der Wurzel keine Quadratzahl steht? Was ist z.B.
die Wurzel aus 7? Nun ist 2² = 4 und 3² = 9 und deshalb
liegt die Wurzel aus 7 zwischen 2 und 3. Klar, der
Taschenrechner liefert es genauer.
Eine andere Möglichkeit ist nach einem schlauen Mann
namens Taylor benannt: „Die Taylor-Reihen Entwicklung
von x + 1 konvergiert für |x| < 1 punktweise gegen den
Funktionswert der Wurzelfunktion.“
x +1 = 1+
1
1
1
5 4
x − x 2 + x3 −
x + ...
2
8
16
128
Wurzel 7 kann man damit nicht berechnen, weil dann x =
6 und damit größer 1 wäre. Aber Wurzel 1,73 kann man
mit x = 0,73 näherungsweise berechnen:
26
1 + 0,73 ≈ 1 +
1
1
1
5
⋅ 0,73 − ⋅ 0,73 2 + ⋅ 0,73 3 −
⋅ 0,73 4 ≈ 1,685
2
8
16
128
Der Taschenrechner liefert natürlich viel schneller einen
exakteren Wert: 1,31529 ....
Wenn man nach Taylor einen besseren Näherungswert
berechnen will, muss man noch ein paar Terme mehr
berechnen, am besten unendlich viele ...
Das (3n+1) – Problem und seine
Verwandten
Unter Mathematikern ist folgendes Problem seit langer
Zeit bekannt, aber noch nicht gelöst:
Man bildet eine Zahlenfolge indem man mit einer
natürlichen Zahl n startet und sie halbiert falls möglich,
sonst bildet man die Zahl 3n+1. Die Folgen enden
anscheinend immer bei 1, was aber bis heute noch
niemand allgemein beweisen konnte. Um das Problem
besser zu verstehen, haben wir verwandte Probleme
untersucht.
Aber zunächst ein paar Beispiele:
Wir starten mit 34. Dann lauten die folgenden Zahlen
27
17, da 34 gerade ist, 52, da 17 ungerade und 3*17+1=52
ist. Weiter geht es mit 26, 13, 40, 20, 10, 5, 16, 8, 4, 2
und schließlich 1. Bei anderen Zahlen kann es länger
dauern bis man bei 1 landet, selbst wenn die Startzahl
klein ist: 18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40,
20, 10, 5, 16, 8, 4, 2, 1.
Bei der relativ kleinen Zahl 27 braucht man über 100
Schritte, während man mit der Startzahl 341 nur 11
Schritte braucht um bei der 1 zu landen.
Auf jeden Fall ist man bei allen bis heute untersuchten
Beispielen immer bei 1 gelandet, kann es aber nicht
beweisen, dass es wirklich bei allen natürlichen Zahlen
passiert. Nur wenn eine Zweierpotenzen auftaucht, weiß
man direkt, dass 1 rauskommen wird, weil diese immer
wieder durch zwei teilbar sind. Wenn man mit einer
Zahlenfolge also eine Zweierpotenz erreicht, weiß man
also sicher, dass man bei einer 1 landet. Aber man kann
auch nicht beweisen, dass man immer auf eine
Zweierpotenz kommt.
Da auch für uns dieses Problem leider nicht zu beweisen
war , haben wir uns mit seinen Verwandten beschäftigt,
28
um es vielleicht besser verstehen zu können. Darunter
verstehen wir Probleme mit einem etwas geänderten
Verfahren mit dem man die Zahlenfolgen erstellt. Dabei
haben
wir
gefunden,
eine
die
wir
Reihe
in
interessanter
den
folgenden
Ergebnisse
Abschnitten
vorstellen wollen.
1. Das (k*n+1)-Problem
Hier wird nur die 3 durch eine andere natürliche Zahl
ersetzt. Dabei haben wir als erstes das simpelste
gewählt: k = 1.
Beispiel: 211, 212, 106, 53, 54, 27, 28, 14, 7, 8,...,1
Wir landen bei der 1 und das muss auch immer so sein,
da die Zahl sich immer halbiert, es sei denn, sie ist
ungerade. Dann wird 1 addiert und sie ist wieder gerade.
Somit kann sie wieder halbiert werden und dadurch wird
sie kleiner als vor der Addition von 1 und muss dann
irgendwann 1 erreichen.
29
Wir haben jetzt erst mal mit ungeraden k weitergemacht
und k = 5 gewählt.
Beispiel: 23, 116, 58, 29, 146, 73, 366, 183, 916,...
Bei k = 5 gehen die Zahlen scheinbar ins Unendliche.
Aber wenn man Glück hat erreicht man irgendwann eine
Zweierpotenz und dann landet man doch noch bei der 1,
wie im folgenden Fall: 204, 102, 51, 256, 128, ..., 1
Wir haben also hier das gleiche Problem wie beim
(3n+1)-Algorithmus und können nicht entscheiden, ob
wir schließlich bei 1 enden oder nicht. Dasselbe gilt für
(7n+1), (9n+1),... usw.
Wie sieht es bei geraden k aus? Zunächst haben wir k =
2 gewählt.
Beispiel: 24, 12, 6, 3, 7, 15, 32, 63, 127, 235, 471, ...
Die Zahlen steigern sich ins Unendliche. Der Grund
dafür liegt dabei, dass wenn man eine Zahl - egal
welche – verdoppelt, kommt immer eine gerade Zahl
heraus. Wenn man zu dieser 1 dazu zählt, kommt
30
folglich immer eine ungerade Zahl raus. Wenn man in
der Folge also einmal eine ungerade Zahl hat, dann
werden die Zahlen nur noch größer. Allerdings führen
auch hier die Zweierpotenzen zur 1, da man sie bis zur 1
runter durch 2 teilen kann.
Da die gleichen Überlegungen für alle geraden k gelten,
wird die Zahlenfolge also immer ins Unendliche
abwandern, es sei denn, man beginnt mit einer
Zweierpotenz.
2. Das (kn+m)-Problem
Da wir 3n+1 schon hatten, nehmen wir einfach mal
seinen Bruder 3n+3.
Beispiel: 56, 28, 14, 7, 24, 12, 6, 3, 12, 6, 3…
Jetzt haben wir eine neue Variante: die 1 kommt nicht
vor aber wir wandern auch nicht nach Unendlich
sondern enden bei 3. Eine Erklärung könnte sein, dass
man 3n+3 auch als 3(n+1) schreiben kann. Wie wir oben
gesehen haben, führt n+1 zur 1 und daher vielleicht
3(n+1) zur 3. Dann müsste man bei 5n+5 immer auf 5
kommen.
31
Beispiel: 7, 40, 20, 10, 5, 30, 15, 80, 40, 20, 10, 5,…
Unsere These scheint zu stimmen. Bei allen x*(n+1)
Algorithmen müsste man dann immer bei x landen. Das
müssen wir noch genauer untersuchen. Interessant ist
auch noch unser folgendes Ergebnis für 3n+5:
56, 28, 14, 7, 26, 13, 44, 22, 11, 38, 19, 62, 31, 98, 49,
152, 76, 38, 19,…
Man landet immer wieder auf einer Zahl (hier 19), die
aber nichts mit 3 oder 5 zu tun hat. Es ist auch nicht
immer die 19, wie das folgende Beispiel zeigt: 46, 23,
74, 37, 116, 58, 29, 92, 46, 23, …
Hier landet man immer wieder bei 23.
Für unsere JuFo-Arbeit haben wir noch viele weitere
Algorithmen untersucht, die wir aber aus Platzgründen
hier nicht vorstellen können. Viele interessante Beispiele
und Vermutungen können in diesem Zusammenhang
noch bearbeitet werden.
32