¨Ubungsblatt 10 - Musterlösungen

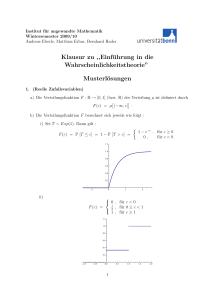
Humboldt-Universität zu Berlin
Institut für Mathematik
Prof. Dr. U. Horst
Stochastik I SS 2013
Übungsblatt 10 - Musterlösungen
1.
[Charakteristische Funktion] Es gilt:
ϕX (u) = E[exp(iuX)]
∞
X
P[X = n] exp(iun)
=
=
n=0
∞
X
λn −λ
e exp(iun)
n!
n=0
∞
X
(λeiu )n
=e
−λ
n!
n=0
= e−λ exp(λeiu )
iu −1)
= eλ(e
2.
.
[Zentraler Grenzwertsatz] Wir nehmen an, dass die Inanspruchnahme der Plätze unabhängig
voneinander erfolgt. Definiere die Zufallsvariable Xi mit
(
1 , falls die Buchung i eingelöst wird
Xi =
0 , falls die Buchung i nicht eingelöst wird.
Dann gilt:
P[Xi = 1] = p :=
270
300
= 0,9
und nach Annahme sind die Xi P
stochastisch unabhängig. Falls n Buchungen für einen Flug
akzeptiert werden, so ist Sn = ni=1 Xi die Anzahl der in Anspruch genommenen Plätze.
Die Zufallsvariable Sn ist binomialverteilt mit Parametern n und p. Da die Rechnung mit
der Binomialverteilung für solch große Werte von n nicht praktikabel ist, verwenden wir
die Normalverteilung als Nährung. Dieses Vorgehen wird durch den zentralen Grenzwertsatz
gerechtfertigt. (Der Fehler, den wir dabei machen, wird deutlich kleiner sein, als der unvermeidbare Modellierungfehler beim Übergang von der komplexen Realität zum einfachen
stochastischen Modell.) Sei
µ := E[Xi ] = p = 0,9 ,
σ 2 := Var(Xi ) = p(1 − p) = 0,09 .
Dann gilt nach dem zentralen Grenzwertsatz:
Pn
Xi − µ
250 − µn
250 − µn
i=1
√
√
≤ √
,
≈Φ
P[Sn ≤ 250] = P
σ2n
σ2n
σ2n
0.9 n + 0.564
n
252
250
248
246
n
262
264
266
268
270
wobei Φ wie üblich die Verteilungsfunktion der Standardnormalverteilung bezeichnet. Es gilt
nun:
250 − µn
250 − µn
√
≥ Φ−1 (0,97)
≥ 0,97 ⇔ √
Φ
2
σ n
σ2n
√
⇔ µn + Φ−1 (0,97) σ 2 n ≤ 250 .
Mit Φ−1 (0,97) ≈ 1,88 erhalten wir die Bedingung:
√
0,9n + 0,564 n ≤ 250 .
Die größte natürlich Zahl, die diese Ungleichung erfüllt, ist n = 267.
3.
[Bedingte Wahrscheinlichkeit]
a) Da Bi eine disjunkte Zerlegung von Ω ist, gilt:
A=
n
[
i=1
(A ∩ Bi )
und (A ∩ Bi ) ∩ (A ∩ Bj ) = ∅ für i 6= j. Es folgt:
"n
#
[
P[A] = P
(A ∩ Bi )
i=1
=
=
n
X
P[A ∩ Bi ]
i=1
n
X
i=1
P[Bi ]6=0
=
n
X
i=1
P[Bi ]6=0
P[A ∩ Bi ]
P[A | Bi ] · P[Bi ] .
b) Mit Teil a) gilt (bemerke, dass P[Bi ] > 0 für i = 1, . . . , n per Annahme):


n
X
P[Bi | A] · 
P[A | Bj ] · P[Bj ] = P[Bi | A] · P[A]
j=1
= P[A ∩ Bi ]
= P[A | Bi ] · P[Bi ] .
4.
[Testfehler] Bemerke, dass Ω = K ∪ K C eine disjunkte Zerlegung von Ω ist. Weiter gilt:
P[AC | K] = 1 − P[A | K] ,
P[A | K C ] = 1 − P[AC | K C ] .
Damit gilt unter Verwendung von Aufgabe 3:
P[A | K] · P[K]
P[A | K] · P[K] + P[A | K C ] · P[K C ]
1
0,96 · 145
=
144
1
+ 0,06 · 145
0,96 · 145
P[K | A] =
= 0,1 .
P[AC | K C ] · P[K C ]
P[AC | K] · P[K] + P[AC | K C ] · P[K C ]
0,94 · 144
145
=
1
144
0,04 · 145
+ 0,94 · 145
P[K C | AC ] =
≈ 0,9997 .
Die Wahrscheinlichkeit, die Krankheit zu haben, wenn der Test positiv ausfällt (P[K | A]),
ist also immer noch relativ gering. Dagegen ist die Wahrscheinlichkeit, bei einem negativen
Testergebnis tatsächlich gesund zu sein (P[K C | AC ]), sehr hoch.