Die Theorie des Monopols

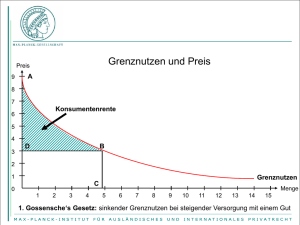
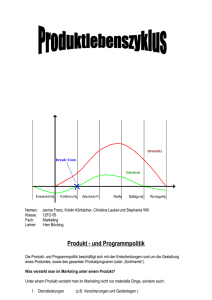
Die Theorie des Monopols
Schülerseminar anlässlich des Wissenschaftsjahrs 2008
Mathematik – 17. September 2008
von
Jr.-Prof. Dr. Ingrid Ott
Hamburgisches WeltWirtschaftsInstitut (HWWI)
Agenda
ƒ Hintergründe
ƒ Marktformen: Wettbewerb, Kartell und Monopol
ƒ Wohlfahrtskonzept
ƒ Theorie
ƒ Diskussion
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 2
Merkmale des vollständigen Wettbewerbs:
Beispiel ‚Markt für Bier‘
ƒ Viele Anbieter
ƒ Einzelne Anbieter können auf den Marktpreis keine
Einfluss nehmen („Preisnehmer“)
ƒ Nachfrager sind vollständig informiert und sehen
alle Kneipen als ein „homogenes Gut“ an
ƒ Produzenten und Konsumenten erreichen hohe
Renten
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Marktgleichgewicht auf dem Markt für Bier
bei vollkommener Konkurrenz
Angebots- und Nachfragefunktion:
Zusammenhang zwischen Preis und Menge
1
GK = 1 +
x
4000
1
P = 5−
x
4000
Schnittpunkt liefert Gleichgewichtspreis und –menge
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 4
Wohlfahrtskonzept:
Konsumentenrente und Produzentenrente
Konsumentenrente:
Differenz zwischen der
Zahlungsbereitschaft und
dem Preis des Produkts
Produzentenrente:
Differenz zwischen dem
Marktpreis und jenem
Preis, zu dem ein
Produzent sein Gut
(gerade noch) anbieten
würde (Reservationspreis)
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 5
Anreiz für Anbieter, den Wettbewerb zu
beschränken
Für Anbieter ist der vollständige Wettbewerb kein anzustrebender
Zustand (Bofinger (2007), Kap.8)
Versuch, den Preis zum Aktionsparameter zu machen, um so
... den Konsumenten einen möglichst großen der Teil der
Konsumentenrente abzunehmen
Formen:
ƒ Kartell, d.h mehrere Anbieter vereinbaren den Preis
gemeinsam (Kollusion). Setzt begrenzte Zahl der Anbieter
sowie Koordination ihres Verhaltens voraus.
ƒ Monopol, nur noch ein Anbieter
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Kartell am Biermarkt: Anbieter beschließen,
4€ zu verlangen
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Effekte
ƒ Die Anbieter erhöhen ihre Produzentenrente von 8000
auf 10000
ƒ Die Konsumenten verlieren Konsumentenrente: statt
8000 nur noch 2000
ƒ Summe von Produzenten- und Konsumentenrente
sinkt von 16000 auf 12000
Fazit: Die gesellschaftliche Wohlfahrt sinkt durch
Wettbewerbsbeschränkungen im Vergleich zur
Situation mit vollständigem Wettbewerb
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 8
Monopol auf dem lokalen Biermarkt
ƒ Alle Bierlokale werden von einem Betreiber
aufgekauft.
ƒ Wie findet dieser den für ihn optimalen Preis?
ƒ Ausgangspunkt: Konzept der Preiselastizität der
Nachfrage:
Um wieviel Prozent verändert sich die
nachgefragte Menge, wenn der Preis um ein
Prozent gesenkt wird?
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 9
Allgemeiner Zusammenhang bei Bewegung
auf Nachfragekurve
Eckpunkte
ƒ Prohibitivpreis: Preis zwar hoch, die nachgefragte
Menge ist aber Null und damit auch der Umsatz.
ƒ Sättigungsmenge: Menge maximal, Preis gleich Null,
Umsatz ist ebenfalls Null
Dazwischen: Umsatz verläuft als Parabel. Steigt an
ausgehend vom Prohibitivpreis, erreicht Maximum
genau bei der halben Sättigungsmenge und fällt dann
wieder auf Null.
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Umsatz: Preis multipliziert mit der Menge
1
⎛
⎞
P*x = ⎜5 −
x ⎟*x
4000 ⎠
⎝
Preis in €
Menge
Umsatz
5.00
0
0
4.50
2.000
9.000
4.00
4.000
16.000
3.50
6.000
21.000
3.00
8.000
24.000
2.50
10.000
25.000
2.00
12.000
24.000
1.50
14.000
21.000
1.00
16.000
16.000
0.50
18.000
9.000
0
20.000
0
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 11
Nachfrage und Umsatz in allgemeiner Form
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Formale Herleitung
U = p(x) x
ƒ mit x als Menge und p als Preis.
Lineare Nachfragefunktion:
p = a – bx,
ƒ Achsenabschnitt a als Prohibitivpreis,
Umsatz dann als Parabel:
U = ax – bx².
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 13
Formale Herleitung (Fortsetzung)
Maximaler Umsatz, wenn wir diese Gleichung nach x
ableiten:
dU/dx = a - 2bx (Grenzerlös)
für dU/dx = 0 folgt x =a/2b.
Die Sättigungsmenge erhalten wir für p=0,
0 =a – bx, d.h.
x=a/b
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 14
Preiselastitzität der Nachfrage
ε x,p = |(Δxn/xn)/(Δp/p)|
Als Betrag definiert, da die Elastizität sonst immer
negativ wäre
ƒ ε > 1: Bereich der Nachfragekurve, der links von
a/2b liegt: Menge steigt über-proportional, wenn
Preis gesenkt wird → Umsatz steigt
ƒ ε < 1: Bereich der Nachfragekurve, der rechts von
a/2b liegt: Menge steigt unter-proportional, wenn
Preis gesenkt wird → Umsatz sinkt
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 15
Was macht der Monopolist mit dieser
Information?
ƒ In Wettbewerbssituation lag der Preis im Bereich mit
ε >1.
ƒ Preissenkung würde also Umsatz erhöhen
ƒ Aber: wegen steigender Grenzkosten nehmen auch die
Kosten zu
ƒ Also: Monopolist muss Preis so setzen, dass sein
Gewinn maximal wird
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 16
Herleitung
ƒ Gewinn = Umsatz - Kosten
ƒ Maximaler Gewinn: Gewinnfunktion ableiten nach x
ƒ dG/dx = dU/dx - dK/dx = 0
-> Grenzerlös=Grenzkosten
ƒ Grafische Lösung für optimale Angebotsmenge:
ƒ Schnittpunkt der Grenzerlös-Kurve mit der Angebotskurve
(Grenzkostenkurve)
ƒ Preis wird dann auf der Nachfrage-Kurve für diese Menge
ermittelt
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 17
Berechnungen
ƒ Nachfragefunktion:
p = 5- 1/4000x
ƒ Umsatz:
U = 5x - 1/4000x²
ƒ Grenzerlös (dU/dx):
GE = 5 - 1/2000x
ƒ Grenzkosten:
(=Angebotskurve)
GK = 1/4000x + 1
ƒ Optimaler Output für Monopolisten (GE=GK):
5-1/2000x=1/4000x-1
x*=5333
ƒ In Nachfragefunktion:
p* = 5 - (1/4000) 5333 = 3 2/3
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 18
Kosten und Umsatz des Monopolisten
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 19
Grafische Darstellung
Auguste Antoine
Cournot
© Pearson Studium 2007
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 20
Vergleich der Wohlfahrt für verschiedene
Marktformen
Konsumenten-
Wettbewerb
Kartell
Monopol
8.000
2.000
3.573,11
8.000
10.000
11.519,28
16.000
12.000
15.092,39
---
4.000
907,61
rente
Produzentenrente
Wohlfahrt
WohlfahrtsVerlust
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 21
Ergebnis für das Monopol
ƒ Es wird wie schon im Kartell weniger angeboten als bei
vollständigem Wettbewerb
ƒ Effekte auf Konsumenten- und Produzentenrente wie
im Kartell-Beispiel, d.h. insgesamt sinkt Wohlfahrt
ƒ Genaue Berechnung des Cournot‘schen Punktes zeigt,
dass Wirte im Kartell-Beispiel einen zu hohen Preis
fixiert haben
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 22
Monopole und Kartelle sind verboten
Gesetz gegen Wettbewerbsbeschränkungen (GWB)
ƒ § 1 Kartellverbot
ƒ § 36: Zusammenschlüsse dürfen nicht zu
marktbeherrschender Stellung führen
ƒ § 19 Abs. Definition einer marktbeherrschenden
Stellung
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 23
Wann liegt eine marktbeherrschende
Stellung vor?
ƒ Bei einem Unternehmen:
Marktanteil von mindestens einem Drittel
ƒ Bei zwei und drei Unternehmen:
Marktanteil von 50 %
ƒ Bei vier und fünf Unternehmen:
Marktanteil von zwei Dritteln
-> Regulierung
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 24
Literatur:
Bofinger, Peter (2007): Grundzüge in die
Volkswirtschaftslehre – Eine Einführung in die
Wissenschaft von Märkten, 2. Auflage
Vielen Dank für Ihr Interesse
Kontakt: [email protected]
Wissenschaftsjahr 2008 Mathematik * Theorie des Monopols * IO * 17.09.2008
Seite 25