Document

4. Steuerinzidenz
•
•
•
•
•
•
•
•
Wer trägt die Last einer Steuer?
Steuerzahler: derjenige, der Steuer abführt.
Steuerträger: derjenige, der die Last trägt. Dies sind nicht
notwendigerweise dieselben Personen.
Lastverteilung bzw. Inzidenz hängt nur von den Marktverhältnissen ab.
Was passiert mit den Steuereinnahmen?
Budgetinzidenz: Betrachtet auch die Verwendung der Ausgaben.
Differentielle Inzidenz: Betrachtet verschiedene Steuern mit
identischem Aufkommen.
Hier zunächst: absolute Inzidenz, d.h. es werden weder Ausgaben
berücksichtigt noch die Senkung anderer Steuern.
4.1. Partielles Gleichgewicht
4.1.1. Vollständiger Wettbewerb
•
Betrachte einen Markt für ein Gut x, z.B. Kaffee. Sei D (q ) die
Nachfrage als Funktion vom Verbraucherpreis q, S ( p ) das Angebot
als Funktion vom Produzentenpreis p.
•
Im Marktgleichgewicht ist Angebot gleich Nachfrage, D (q ) = S ( p ) .
•
Erhebung einer Mengensteuer mit Satz t.
•
Konsumenten führen die Steuer ab: Nettopreis p; aus Sicht der
Nachfrager steigt der Bruttopreis auf q = p + t .
•
Anbieter führen die Steuer ab: Bruttopreis q; aus Sicht der Anbieter sinkt
der Nettopreis auf p = q − t
•
Im Endergebnis ist Inzidenz unabhängig davon, welche Marktseite die
Steuer abführt. Im Gleichgewicht gilt D q = S p
also
oder
D( p + t ) = S ( p )
D(q ) = S (q − t )
( )
( )
Ohne Steuer:
q= p
p
S ( p)
p1
D( p )
x
x1
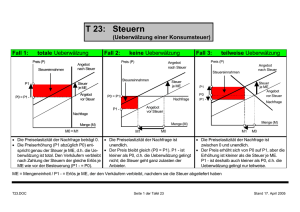
1.Fall: Konsumenten führen die Steuer ab:
q = p+t
•
Für Produzenten ist Nettopreis und die davon abhängige Angebotskurve
entscheidend: S p
•
Nachfrage orientiert sich an Bruttopreisen
( )
p
D (q ) = D ( p + t )
S ( p)
p2 + t
p1
p2
D( p )
D( p + t )
x2
x1
x
p = q −t
2.Fall: Produzenten führen die Steuer ab:
•
Für die Nachfrager ist der Bruttopreis und die davon abhängige
Nachfragekurve entscheidend: D q
•
Produzenten orientieren sich an Nettopreisen
( )
S (q − t )
q
S ( p ) = S (q − t )
S (q )
q2
q1
q2 − t
D(q )
D( p + t )
x2
x1
x
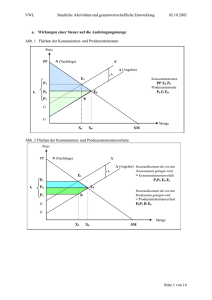
Ergebnis:
•
Die umgesetzte Menge des besteuerten Gutes sinkt von x1 auf x2 .
•
Im Gleichgewicht steigt der Bruttopreis und der Nettopreis sinkt:
- Die Nachfrager zahlen einen um q2 − q1
- Die Anbieter erhalten einen um
p1 − p2
höheren Bruttopreis.
geringeren Nettopreis.
•
Beide Marktseiten tragen somit einen Teil der Steuer.
•
Die Summe der absoluten Preisänderungen entspricht dem
Steuerbetrag.
•
Diese Resultate gelten unabhängig davon, welche der Parteien formal
zur Steuerzahlung verpflichtet ist.
Sind die Konsumenten zahlungspflichtig, dann werden sie einen Teil der
Steuer durch Verringerung der Nettopreise auf die Anbieter rückwälzen.
Sind die Produzenten steuerpflichtig, werden sie einen Teil der Steuer
durch Erhöhung der Bruttopreise auf die Nachfrager vorwälzen.
Wovon hängt die jeweilige Steuerbelastung der beiden Marktparteien ab?
•
Frage nach der Verteilung der reinen Zahllast , nicht der steuerlichen
Verzerrungen (Zusatzlast).
•
Maß der Lastenverteilung: Wie ändert sich der Bruttopreis q wenn sich
der Steuersatz t ändert?
⎧1
dq ⎛ ∆q ⎞ ⎪
⎜=
⎟ = ⎨1 2
dt ⎝ ∆t ⎠ ⎪
⎩0
•
alleinige Belastung der Nachfrager
hälftige Lastteilung
alleinige Belastung der Anbieter
Definiere Preiselastizitäten
∂S ( p ) p
Angebotselastizität : ε =
⋅
∈ [0, ∞ ]
∂p S ( p )
S
Nachfrageelastizität : ε
D
∂D( p ) p
=
⋅
∈ [− ∞,0]
∂p D( p )
=> normale Angebots- und Nachfragereaktionen
•
Marktgleichgewicht:
D ( p (t ) + t ) = S ( p (t ))
•
Differenzieren:
⎛ dp ⎞
' dp
D ⋅ ⎜ + 1⎟ = S ⋅
dt
⎠
⎝ dt
'
•
Umstellen:
dp
D'
= '
dt S − D '
•
Aus q (t ) = p (t ) + t folgt:
dq dp
S'
=
+1 = '
dt dt
S − D'
•
Ausgehend vom Wert t = 0 ergibt sich unter Verwendung von D
und p = q folgende Lastverteilung, ausgedrückt in Elastizitäten:
dp
D' ⋅ p D
= '
dt S ⋅ p D − D ' ⋅ p D
D' ⋅ p D
εD
= '
= S
'
S ⋅q S − D ⋅ p D ε −ε D
•
Die Veränderung der Bruttopreise bei marginaler Einführung des
Steuersatzes t ist dann
εD
dq dp
=
+1 = S
+1
D
dt dt
ε −ε
oder
dq
εS
= S
dt ε − ε D
∈ [0,1]
=S
1.Fall:
εD =0
D (q )
q
oder
εS =∞
dq
dp
= 1,
=0
dt
dt
:
q
S (q − t )
D (q )
S (q − t )
S (q )
t
t
S (q )
x
Nachfrage vollkommen unelastisch oder
x
Angebot vollkommen elastisch
Intuition: Nachfrage können Gut nicht substituieren oder Anbieter können
perfekt ausweichen und ihr Produkt auf anderen Märkten anbieten.
=> Alleinige Belastung der Nachfrager durch die Steuer
2.Fall:
p
εS =0
oder
εD =∞:
S ( p)
t
dq
dp
= 0,
=1
dt
dt
S(p)
p
D(p)
t
D( p + t )
D( p + t )
x
Angebot vollkommen unelastisch
oder
D( p )
x
Nachfrage vollkommen elastisch
Intuition: Das Angebot ist gegeben und auf andere Märkte kann nicht ausgewichen werden oder Nachfrager können perfekt das Gut substituieren.
=> Alleinige Belastung der Anbieter durch die Steuer
3.Fall:
ε = −ε
S
D
:
dq 1 dp 1
= ,
=
dt 2 dt 2
S (q − t )
p, q
S (q )
q2 = p2 + t
p1 = q1
p2 = q2 − t
D(p)
D( p + t )
x2
x1
=> Hälftige Lastteilung zwischen Anbietern und Nachfragern
x
Hauptergebnisse:
•
Der von einer Marktseite zu tragende Steueranteil ist umso
größer, je unelastischer diese Marktseite reagiert und je
elastischer die andere Marktseite reagiert.
•
Weil die Lastverteilung nur von den Elastizitäten des
Angebots und der Nachfrage abhängt, ist sie unabhängig
von der formalen (rechtlichen) Zahlungsverpflichtung.
Anmerkung: Die Lastverteilung bei einer Wertsteuer q = p (1 + t )
unterscheidet sich nicht von der Lastverteilung einer Mengensteuer.
Sie wird in gleicher Weise durch die Elastizitäten des Angebots und der
Nachfrage bestimmt.
Anwendungen
Kaffeesteuer
•
Was passiert, wenn Deutschland (alleine) eine Kaffeesteuer einführt?
Wirkt wie ein Zoll auf Kaffeeimporte.
•
Ann.: Deutsche Kaffeenachfrage hat keinen Effekt auf WeltmarktNachfrage.
•
Angebot ist vollkommen elastisch: Anbieter müssen in Deutschland
denselben Nettopreis erhalten wie anderswo, um hier zu verkaufen.
•
Folge: Wenn Nachfrageelastizität endlich ist, tragen Nachfrager die
gesamte Steuerlast.
=> Gilt allgemein für homogene Güter, die auf wettbewerblichen Weltmärkten
gehandelt werden und bei denen der Marktanteil des betrachteten
Landes vernachlässigbar ist.
•
Wenn alle Nachfragerländer gemeinsam die Kaffeesteuer erhöhen,
können Produzenten nicht ausweichen: Wenn Produktion kurzfristig
vollkommen unelastisch ist, die Nachfrage aber begrenzt elastisch,
tragen Anbieter die gesamte Steuerlast!
Anwendungen
Bodensteuer
•
Angebot an Boden ist vollkommen unelastisch: Grundbesitzer tragen
gesamte Last einer Bodensteuer.
•
Seien die Erträge des Bodens aus Miete oder Pacht in der Zukunft
y1 , y2 ,... . Erträge zukünftiger Jahre werden mit Zinsfaktor 1 + r
abgezinst. Bodenwert entspricht dann dem Barwert der Erträge:
∞
Bodenwert vor Steuern = ∑
ys
s
(
)
1
+
r
s =0
•
Mit einer Steuer mit Satz t, die der Eigentümer zahlt, sinkt der Barwert
∞
auf
ys − t
Bodenwert nach Steuern = ∑
s
(
)
1
+
r
s =0
•
Steuer wird im Bodenwert kapitalisiert. Nachfrager vermindern Gebote
um den Barwert der Steuern und der Eigentümer trägt die volle Last.
•
Allerdings werden nicht antizipierte Bodensteuern vom Käufer
getragen.
Anwendungen
Gebäudesteuer
•
Grundsteuer (Deutschland): Kombinierte Steuer auf Boden- und
Gebäudewert.
•
Ann.: Bauherren verlangen eine Mindestverzinsung (Kapitalmarktzins +
Risikoprämie) für Neubauprojekte! Ansonsten wählen Kapitaleigentümer
andere Anlageformen: Angebot von Neubauten ist vollkommen
elastisch.
•
Steuer wird von Nachfragern getragen.
•
Aber: unerwartete Gebäudesteuer wird von den Anbietern getragen
(solange Nachfrage elastisch ist), weil sie den Gebäudebestand
kurzfristig nicht anpassen können! Inzidenz hängt vom betrachteten
Zeithorizont ab.
Anwendungen
Lohnsteuer
•
Unternehmen: Arbeitsnachfrage als Funktion des Brutto-Reallohns,
LD (w p )
•
Haushalte: Arbeitsangebot als Funktion des Netto-Reallohns
•
Ergebnis: Der Nettolohn sinkt umso mehr, je elastischer die
Arbeitsnachfrage und je unelastischer das Arbeitsangebot.
•
Empirisch ist die Arbeitsangebotselastizität gering (zumindest für
Männer); Arbeitsnachfrage elastisch (Substitution durch Kapital,
Abwanderung ins Ausland...).
•
Fazit: Arbeitnehmer tragen den Großteil der Last.
LS ((1 − t )w p )
Anwendungen
Lohnsteuer
•
Ausnahme: Profifußballer, die kostenlos ins Ausland wechseln können,
wenn Nettolöhne dort höher sind (idealisierende Annahme)! Angebot
vollkommen elastisch.
•
Da Verein nicht ins Ausland wechseln kann, ist Nachfrage eher
unelastisch: Verein trägt die gesamte Steuerlast.
•
Ähnlich: Spitzen-Manager, Künstler, Wissenschaftler...
•
Aber: Je immobiler die Arbeitnehmer, desto größer ihr Anteil an der
Steuerlast.
Anwendungen
Kapitaleinkommensteuer
Geschlossene Volkswirtschaft:
•
Kurzfristig wird die Steuer allein von den Kapitaleigentümern getragen,
da sie ihre Investitionen in der Vergangenheit vorgenommen haben.
•
Langfristig kann Kapitalangebot durch verringerte Ersparnis gesenkt
werden. De Lastverteilung hängt dann davon ab, wie elastisch die
Kapitalnachfrage ist. Empirisch: Kapitalnachfrage elastisch,
Kapitalangebot unelastisch
=> Kapitalanbieter tragen Steuer auch langfristig.
Anwendungen
Kapitaleinkommensteuer
Offene Volkswirtschaft:
r*
•
Internationaler Kapitalmarkt mit gegebenem Weltmarktzins
•
Der inländische Nettozins r − t muss dem Weltmarktzins
entsprechen, wenn Investitionen im Inland interessant sein sollen:
Kapitalmarktgleichgewicht : r = r * + t
•
Eine Steuer auf Kapitaleinkommen wird dann durch Zunahme des
Bruttozinses in Höhe der Steuer ausgeglichen: Kapitaleigentümer
können der Steuer vollständig ausweichen!
•
Gesamtwirtschaftliches Modell:
Unternehmen produzieren mit Arbeit N und Kapital K.
Produktionsfunktion mit konstanten Skalenerträgen:
Gewinn:
π = F (N , K ) − w ⋅ N − r ⋅ K
F (N , K )
Kapitaleinkommensteuer
Offene Volkswirtschaft:
•
Im Wettbewerbsgleichgewicht konkurrieren die Unternehmen sich
herunter auf einen Gewinn von Null:
π = 0 ⇔ F (N , K ) = w ⋅ N + r ⋅ K
•
Das gesamte Inlandsprodukt wird durch das Arbeits- und das
Zinseinkommen ausgeschöpft (Ausschöpfungstheorem).
•
Weil die Kapitaleinkommensteuer nicht von den Kapitaleigentümern
getragen wird, liegt die Inzidenz allein bei den Arbeitnehmern.
w ⋅ N = F (N , K ) − r ⋅ K
Beweis:
w ⋅ N = F (N , K ) − r * ⋅ K − t ⋅ K
Ableiten nach Steuerbetrag:
∂ (w ⋅ N ) ⎛ ∂F
∂K
*⎞
=⎜
− r ⎟⋅
−1
∂ (t ⋅ K ) ⎝ ∂K
⎠ ∂ (t ⋅ K )
*
Bei t = 0 gilt im Gewinnmaximum ∂F ∂K = r
so dass
∂ (w ⋅ N )
= −1
∂ (t ⋅ K )
Einsetzen von r = r + t
*
ergibt:
Anwendungen
Kapitaleinkommensteuer
Offene Volkswirtschaft:
Ergebnis: Auf Wettbewerbsmärkten mit konstantem Arbeitsangebot und
konstanten Skalenerträgen liegt die Steuerlast einer Kapitaleinkommensteuer, die ausgehend vom Wert t = 0 marginal erhöht
wird, vollständig bei den Arbeitnehmern.
•
Obwohl die Arbeitnehmer nichts mit der Steuerzahlung zu tun haben,
wird die Steuer über eine Lohnsenkung auf sie quergewälzt.
•
Sind die Löhne auf dem Arbeitsmarkt nicht flexibel, dann erfolgt die
Überwälzung der Steuer nicht durch Lohnreduktion sondern durch
eine Verminderung der Beschäftigung: erhöhte Arbeitslosigkeit.
•
Allgemein: Reagiert von zwei Produktionsfaktoren einer elastisch und
der andere unelastisch, dann trägt der letztere Faktor jede Steuer.
Der formale Ansatzpunkt der Steuer ist dabei unerheblich.
Anwendungen
Mehrwertsteuer
•
Unternehmen führen Mehrwertsteuer auf ihre Produkte ab.
•
Entweder erhöhen sich bei gegebenen Nettopreisen dadurch die
Bruttopreise. Die Konsumenten können bei gegebenem Einkommen
weniger konsumieren => Vorwälzung der Steuer auf Verbraucher.
Vorwälzung : (1 + t ) pc = w
•
Oder bei gegebenen Bruttopreisen sinken die Nettopreise. Wenn die
Unternehmen profitabel bleiben wollen, werden sie die gezahlten
Einkommen für ihre Produktionsfaktoren reduzieren => Rückwälzung
der Steuer auf die Einkommensbezieher.
Rückwälzung : pc = w (1 + t ) ≡ (1 − τ ) w falls τ = t 1 + t
•
Belastung derselben Personen als Verbraucher/ Einkommensbezieher.
•
Mehrwertsteuer hat vergleichbare Inzidenzwirkungen wie Steuer auf
Arbeitseinkommen, Bodeneinkommen etc., während Kapitaleinkommen
durch sie nicht belastet werden.
4.1.2. Monopol
•
Was bedeutet Marktmacht für Inzidenz? Kann Monopolist Steuern
vollkommen überwälzen?
•
Bsp. Lineare Nachfrage:
•
Monopolist maximiert Gewinn:
D(q ) = a − q
c
, konstante Grenzkosten
Max π M = (q − t )(a − q ) − c ⋅ (a − q )
(1)
q
•
Bedingung erster Ordnung:
a−q−q+t +c = 0
a+t +c
M
⇔q =
2
•
Aus (1) folgt mit dem Envelopetheorem und (2) an der Stelle
dπ M
dt
(
= − a−q
t =0
M
)
(2)
t=0
a −c−t
a−c
=−
=−
<0
2
2
Inzidenz beim Monopol
q
A
B
q1
D
q0
c+t
E
c
F
GE
x1
x0
D(q )
x
Ergebnis:
•
•
•
Monopolist trägt einen Teil der Steuerlast.
Monopolist setzt GE = c + t ; vor Steuern ist optimale
Produktionsmenge x0 , nach Steuern x1
Gewinn sinkt von q0 DFc auf q1 BE (c + t );
Konsumentenrente sinkt von ADq0 auf ABq1 .
4.2. Allgemeines Gleichgewicht
• Partielles Gleichgewicht untersucht Anbieter- und Nachfragerverhalten
auf einem Markt
• Steuer auf einem Markt hat aber auch Wirkungen auf Verhalten in
anderen Märkten.
• Bsp: Steuer auf Kaffee. Konsumenten fragen weniger Kaffee und mehr
Tee nach.
• Dadurch werden die relativen Preise verändert, die Produktion und die
Faktoreinkommen in beiden Märkten.
• Im Allg. ist die Inzidenz von Steuern über die Märkte hinweg kompliziert,
muss aber für die wesentlichen Märkte erfasst werden, da eine
Vernachlässigung zu gravierenden Effekten und einer falschen
Bewertung von Steuermaßnahmen führen kann.
• Grund: Steuern in einem Sektor können auf andere Sektoren
weitergewälzt werden.
4.2.1 Ein-Sektor-Modell
• Betrachte eine Ökonomie mit nur einem Gut X und zwei
Produktionsfaktoren K und L.
• Produktionsfunktion X = F (K , L )
mit konstanten Skalenerträgen:
λX = F (λK , λL )
Mit λ = 1 L :
X = F (K , L ) = L ⋅ F (K L ,1) = Lf (K L )
Differenzieren nach K und L ergibt
∂F ∂K = f ' (K L )
∂F ∂L = f (K L ) − (K L ) ⋅ f ' (K L )
Daraus folgt Ausschöpfungstheorem (Euler-Theorem):
•
X = F (K , L ) = Lf (K L ) = L ⋅ ∂F ∂L + K ⋅ ∂F ∂K (1)
Firmen maximieren Gewinn π = F (K , L ) − wL − rK (Outputpreis =1)
• Optimale Faktornachfrage ohne Steuern
∂ F ∂ L = FL ( K , L ) = w
∂ F ∂ K = FK ( K , L ) = r
• Bei konstanten Skalenerträgen sind maximale Gewinne = Nullgewinne:
Aus (1) folgt:
F (K , L ) − wL − rK = 0
1. Betrachte Steuer auf Kapital. Annahme: Kapitalangebot (Kapitalstock)
ist fix. Kapitalmarktgleichgewicht: K N = K
Da Kapitalangebot unelastisch ist, fällt Kapitalverzinsung r in Höhe der
Steuer, so dass die Kapitalanbieter die gesamte Steuerlast tragen.
2. Betrachte Mengensteuer auf Arbeit. Inzidenz hängt nun von
Arbeitsangebots- und Arbeitsnachfrageelastizität ab.
t L sind die Gewinnmaximierungsbedingungen:
(3) FK (K , L ) − r = 0
FL ( K , L ) = w + t L ≡ ω
Beim Steuersatz
(2)
•
Änderung der Nachfrage nach Arbeit bei steigender Steuer
Differenziere (2):
N
dL
1
=
< 0 da FLL (K , L ) < 0
dω FLL (K , L )
•
Arbeitsangebot ist eine Funktion des Lohnes:
•
Gleichgewicht auf Arbeitsmarkt:
LA (w) mit ∂LA ∂w > 0
LN (w + t L ) = LA (w)
•
Lohn und Kapitalrendite im Gleichgewicht werden durch folgendes
Gleichungssystem bestimmt:
( 2 ) FL ( K , L ) = w + t L = ω
( 3 ) FK ( K , L ) = r
(5) LN (w + t L ) = LA (w)
( 4) K N = K
•
Im Gleichgewicht hängen Lohn und Kapitalzins vom Steuersatz
•
Einsetzen in (2):
w = w(t L ); r = r (t L )
(
Differenzieren nach t:
Multiplizieren mit
)
FL K , LA (w(t )) = w(t ) + t
∂LA dw dw
(6) FLL ⋅
=
+1
∂w dt
dt
dLN dω = 1 FLL
und umstellen ergibt:
dw ⎛ ∂LA ∂LN
⎜⎜
−
dt ⎝ ∂w ∂ω
⎞ ∂LN
⎟⎟ =
⎠ ∂ω
w
⋅
L
tL
ab:
•
Verwendung der Lohnelastizität von Arbeitsnachfrage und –angebot:
ergibt
•
A
N
∂
∂
ω
L
w
L
A
N
η =
>0
η =
<0
A
N
∂w L
∂ω L
dw
ηN
= A
<0
N
dt η − η
Einsetzen von (3) in (1) ergibt unter Verwendung von (4) und (5):
(
)
(
)
F K , LA (w(t )) − LA (w(t )) ⋅ FL K , LA (w(t )) = r (t ) ⋅ K
•
Differenzieren
A
dr
∂LA dw ∂LA dw
∂
L
dw
A
K
= FL ⋅
−
FL − L FLL ⋅
dt
∂w dt ∂w dt
∂w43
dt
142
•
Verwenden der Elastizitäten:
dw
+1
dt
dr
L ⎛ dw ⎞
L ηA
=− ⎜
+ 1⎟ = −
<0
A
N
dt
K ⎝ dt
K η −η
⎠
Ergebnis:
1. Wer trägt die Last einer Steuer auf den Faktor Arbeit?
Im Allg. trägt Kapital einen Teil der Steuer, und zwar umso
mehr, je elastischer das Arbeitsangebot η A groß und je
unelastischer die Arbeitsnachfrage η N klein .
(
(
)
)
2. Intuition: Je größer die Angebotselastizität, desto weniger
kann der Nettolohn sinken. Je unelastischer die
Arbeitsnachfrage, desto weniger können Firmen K und L
substituieren und Steuer auf Arbeit wirkt wie eine Steuer auf
Kapital.
3. Die Inzidenz abhängig von
- Nachfragereaktion im besteuerten Sektor
- Substitution zwischen den Faktoren
- Elastizität des Angebots der Faktoren
Ergebnis:
4. Ausnahmen:
a. Arbeitsangebot vollkommen unelastisch
dr
dw
⎛ A
⎞
→
0
⇒
→
0
;
→
−
1
η
⎜
⎟
⎝
dt
dt
⎠
Arbeitnehmer können der Steuer nicht ausweichen.
b. Arbeitsnachfrage vollkommen elastisch
dr
dw
⎛ N
⎞
→
−∞
⇒
→
0
;
→
−
1
η
⎜
⎟
dt
dt
⎝
⎠
Kapital und Arbeit perfekte Substitute. Wenn Bruttolohn >
Kapitalzins, fragen Firmen nur noch Kapital nach =>
Nettolohn muss um den vollen Steuerbetrag fallen.
c. Umgekehrt trägt die Last lediglich der Kapitaleigner, wenn
das Arbeitsangebot vollkommen elastisch oder die
Arbeitsnachfrage vollkommen unelastisch ist.
4.2.2 Zwei-Sektoren-Modell (Modell von Harberger (1962))
• Betrachte eine Ökonomie mit zwei Gütern X und Y und zwei
Produktionsfaktoren K und L.
(
)
• Produktionsfunktion X = F K X , LX und Y
konstanten Skalenerträgen => keine Gewinne.
= G (KY , LY )
mit
• Kapital und Arbeit können in beiden Sektoren eingesetzt werden:
K = K X + K Y ; L = LX + LY
• Steuern: Allg. Konsumsteuer (mit Satz t ), selektive Gütersteuer auf X
(mit Satz t X ) , Faktorsteuern auf Arbeit und Kapital (mit Sätzen t K , t L )
• Betrachte Verbrauchsteuer (ad valorem) auf Gut X.
• Annahme: Produktion von X ist relativ kapitalintensiv.
Inzidenz einer speziellen Verbrauchsteuer in der EdgeworthBox
KY
0
y
L
LY
A
α
K X KY
>
LX
LY
LX
B
F Lx
F Ly
=
x
y
F
F
K
K
{
{
GRtS
X
LK
β
0x
KX
K
GRtS
Y
LK
•
Produktionsfaktoren L und K werden effizient eingesetzt, da ihre
relativen Preise durch die Steuer nicht verzerrt werden:
Entlang der Kurve O X BAO Y (wie in den Punkten A und B) stimmen
die technischen Grenzraten der Substitution zwischen L und K für
X
Y
beide Sektoren überein GRtS LK
(Produktionseffizienz)
= GRtS LK
•
Da die Kurve unterhalb der der Diagonalen OX OY verläuft, ist die
Produktion von X kapitalintensiver als die von Y: K X L X > K Y
LY
•
Jeder Punkt auf der Kurve O X BAO Y
bestimmt eine
Produktionskombination von (X,Y), die effizient produziert wird. Alle
effizienten Produktionskombinationen lassen sich auf einer
Transformationskurve im Güterraum X-Y darstellen.
•
Hinzufügung der Indifferenzkurven des repräsentativen Konsumenten:
Bei unverzerrender Besteuerung (Pauschalsteuer) befindet sich die
Gleichgewichtsallokation z.B. im Punkt A.
Produktionsmöglichkeitenkurve
Y
P
Steigung: pX pY
A
GRSXY = GRTXY
O
γ
P
X
•
Da durch die Pauschalsteuer die relativen Preise der Güter nicht
verzerrt werden, passen sich Produzenten und Konsumenten diesem
unverzerrten Preisverhältnis an, so dass gilt:
GRS XY = p X pY = GRTXY
•
Wird nun eine aufkommensgleiche Verbrauchsteuer auf das Gut X
erhoben, so wird der relative Güterpreis verzerrt. Dadurch wird ein Keil
zwischen die Grenzrate der Substitution und die Grenzrate der
Transformation getrieben:
GRS XY
p X (1 + t X ) p X
=
>
= GRTXY
pY
pY
Der Preis für das Gut X erhöht sich für die Konsumenten, weshalb sie
sich an dem Nach-Steuer-Preisverhältnis orientieren. Für die
Produzenten ist hingegen weiterhin das Vor-Steuer-Preisverhältnis
relevant.
•
Punkt B befindet sich aber auf der Transformationskurve PP, da
weiterhin mit der effizienten Faktorkombination produziert wird.
Steigung: pX pY in B
Y
Steigung: pX pY in A
B
GRSXY > GRTXY
A
pX (1+ t X )
Steigung:
pY
O
X
•
Die Konsumentenentscheidung wird aufgrund des höheren
Konsumentenpreises für X verzerrt, indem eine geringere Nachfrage
nach X und eine höhere Nachfrage nach Y entsteht.
•
Dadurch sinkt der Preis für das Gut X und steigt der Preis für Gut Y.
Deshalb ist die Steigung der Gerade für den relativen Preis in Punkt B
niedriger als in A: p X pY ↓
•
Die Unternehmen passen sich mit einer weiterhin effizienten
Produktionsweise an die veränderten Konsumentscheidungen an und
erhöhen die Produktion von Y auf Kosten der Produktion von X.
•
Dadurch erhöht sich die Kapitalintensität in beiden Sektoren:
Eine effizient produzierte Güterkombination XY, bei der weniger von X
und mehr von Y produziert wird, muss auf der Kurve O X BAO Y links
unterhalb von Punkt A liegen. Die Sekanten von der Ursprüngen zu
den Punkten A und B verlaufen nach B flacher als nach A. Die
Steigungen der Sekanten geben vom jeweiligen Ursprung aus
gesehen die Arbeitsintensivitäten an. Da diese Steigungen beim
Übergang von A nach B sinken, muss die Arbeitsintensivität in beiden
Sektoren sinken und folglich die Kapitalintensität steigen.
Verbrauchsteuer auf X erhöht Kapitalintensität in beiden
Sektoren (von Punkt A zu Punkt B)
KY
0
y
L
LY
KY
LX
B
LY
<
KY
A
A
B
LX
KX
0x
LY
KX
B
LX
<
KX
A
K
•
Anstieg der Kapitalintensitäten in beiden Sektoren ist bei gleichzeitiger
Vollbeschäftigung der Faktoren nur möglich, wenn der relative Preis für
Kapital sinkt:
r
r
wB
•
<
wA
Grund: Unternehmen produzieren mehr Y. Da X kapitalintensiv ist, wird
relativ viel Kapital freigesetzt: Verhältnis Kapitalrendite/ Lohn (r/w)
sinkt, damit Kapital weiterhin vollständig eingesetzt wird.
Ergebnis:
Verbrauchsteuer auf X verringert das Faktorpreisverhältnis r/w, wenn X
relativ kapitalintensiv produziert wird.
Somit ändert sich das Verhältnis von Lohn- zu Kapitaleinkommen zu
Lasten des Kapitaleinkommens.
Würde X arbeitsintensiv produziert, so würde der relative Preis für
Kapital r/w steigen.
Relativer Preis der Faktoren r/w sinkt aufgrund der Verbrauchsteuer auf kapitalintensiv produziertes Gut X
KY
0
y
L
r
r
= tan α >
= tan β
wA
wB
LY
A
α
LX
B
β
0x
KX
K
Allgemeines Resultat:
Eine spezielle Verbrauchsteuer auf ein Gut senkt den relativen Preis
des Produktionsfaktors, der relativ intensiv in der Produktion des
besteuerten Gutes verwendet wird.
Folgende Faktoren haben Einfluss:
•
Faktorintensitäten: Je verschiedener die Faktorintensitäten der beiden
Sektoren sind, desto stärker müssen sie sich beim Übergang von A
nach B ändern und umso größer ist die Veränderung von r/w.
•
Preiselastizität der Nachfrage nach X: Je größer die Elastizität der
Nachfrage nach X im Verhältnis zu Y ist, desto größer ist der steuerlich
bedingte Nachfragerückgang nach X und somit die Veränderung des
relativen Kapitalpreises r/w. (unelast.Nachfrage => keine Änderung r/w)
•
Substitutionselastizität von K und L: Je geringer die Substitutionselastizität in der Produktion von X und Y ist, umso stärker sind die
Isoquanten gekrümmt und umso größer ist die Änderung von r/w.
Anwendung:
Wie wirkt sich eine Verringerung des Mehrwertsteuersatzes im Hotelund Gaststättengewerbe aus?
Ann: Vollbeschäftigung; Hotelgewerbe relativ arbeitsintensiv
•
Nachfrage in diesem Sektor steigt relativ zu anderen Sektoren.
•
Verstärktes Dienstleistungsangebot in diesem Sektor.
•
Arbeitsintensität sinkt tendentiell in den Sektoren; Kapitalintensität steigt.
•
r/w sinkt, d.h. der relative Preis für Arbeit (Lohn/Kapitalrendite) steigt.
•
Ist das Arbeitsangebot fix, reagiert also nicht mit einer Zunahme bei
steigendem relativen Preis, dann steigt der relative Preis für Arbeit
besonders stark.
Ergebnis: Eine verringerte Mehrwertsteuer in einem arbeitsintensiven
Sektor erhöht das Lohneinkommen relativ zum Kapitaleinkommen, wenn
Vollbeschäftigung in geschlossener Ökonomie herrscht.
Anwendung: Verringerte Mehrwertsteuer in arbeitsintensivem
Sektor
KY
0
y
L
LY
B
A
L
K
LX
0x
KX
B
L
<
K
A
K