Naturwissenschaften II (B. Sc. Maschinenbau) - IAP TU

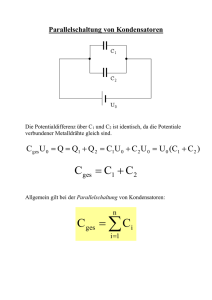
Übungen zur Vorlesung
Naturwissenschaften II
(B. Sc. Maschinenbau)
Sommersemester 2008
Musterlösung 3
Professor Dr. G. Birkl, Dr. N. Herschbach
Besprechung in der Woche
vom 5.5 - 12.5.08
www.physik.tu-darmstadt/apq/naturwissenschaften
1. Elektrisches Feld einer homogen geladenen Vollkugel
Eine Vollkugel mit Radius R = 0.5 m sei mit einer homogenen Ladungsverteilung der
Ladungsdichte ρ0 = 10−6 C/m3 ausgefüllt.
a) Bestimmen sie die Gesamtladung Q dieser Kugel.
b) Berechnen sie den Verlauf des elektrischen Feldes als Funktion des Abstandes r
vom Mittelpunkt der Kugel, sowohl für r ≤ R als auch für r ≥ R. Verwenden Sie
den Gauß’schen Satz.
c) Eine Probeladung der Ladung q wird aus sehr großer Entfernung auf den Abstand
r vom Kugelmittelpunkt der Ladungsverteilung herangebracht. Welche mechachische Arbeit muss hierzu aufgewendet werden? Bestimmen Sie daraus den Verlauf
des elektrostatischen Potentials für 0 ≤ r ≤ ∞. Welche Spannung U liegt an der
Kugeloberfläche?
d) Man kann sich diese Kugel als Elektrode eines Kondensators vorstellen, wobei
die Gegenelektrode unendlich weit entfernt liegt bei dem Potential ϕ(∞) = 0.
Was ist die Kapazität dieses Kondensators? Benutzen der Resultate aus a) und
c) bietet sich hierzu an.
J̀
J́
^
a) Die Ladung der Kugel ergibt sich aus dem Volumenintegral:
R
RR
Q = Kugel ρ0 dV = 0 ρ0 4πr 2 dr = ρ0 34 πR3 = 0.524 · 10−6 C .
b) Aus der Kugelsymmetrie des Problems ergibt sich, dass das elektrische Feld radial ausgerichtet ist, und betraglich nur vom Abstand r vom Kugelmittelpunkt
abhängt. Bei der Anwendung des Gauß’schen Satzes benutzen wir sphärische
Oberflächen
Sr mit Radius r die konzentrisch mit der Kugel sind:
H
2
~
~ = |E(r)|4πr
~
E(r)·d
A
= E(r)4πr 2 . Die Ladung die von einer solchen sphärischen
Sr
Oberfläche Sr eingeschlossen wird ist:
( Rr
Z
ρ0 0 4πr 0 2 dr 0 für r ≤ R,
RR
ρ(r)dV =
ρ0 0 4πr 0 2 dr 0 für r ≥ R.
(
ρ0 34 πr 3 für r ≤ R,
=
ρ0 34 πR3 für r ≥ R.
1
Der Gauß’sche Satz
H
~
~=
E(r)
· dA
Sr
1
0
R
ρ(r)dV ergibt schließlich
(
ρ0 34 πr 3 für r ≤ R,
1
E(r) =
4π0 r 2 ρ0 43 πR3 für r ≥ R.
(
ρ0
r
für r ≤ R,
= ρ300R3 1
für r ≥ R.
30 r 2
c) Die mechanische Arbeit W (r) die Rbei AnnäherungR bis zum Abstand r aufzubrinr
~ · d~s = − r qE(r 0 )dr 0 .
gen ist ergibt sich aus: W (r) = − ∞ q E
∞
R r 0 R3 1 0
ρ0 R 3 1
Für r ≥ R wird das W (r) = − ∞ ρ3
.
dr
=
q
2
30 r
0 r0
Und für r ≤ R:
Z R
Z r
0
0
W (r) = −
qE(r )dr −
qE(r 0 )dr 0
∞
R
Z r
Z R
3
ρ0 0 0
ρ0 R 1 0
dr − q
r dr
q
=−
0
30 r 2
R 60
∞
r
ρ0 R 3 1
ρ0 r 0 2
=q
−q
30 R
30 2 R
ρ0
r 2 R2
2
+
=q
R −
30
2
2
ρ0
2
2
(3R − r ).
=q
60
Das elektrostatische Potential ergibt sich aus ϕ(r) = W (r)/q.
(
ρ0
(3R2 − r 2 ) für r ≤ R,
60
ϕ(r) = ρ0 R3
für r ≥ R.
30 r
Die Spannung auf der Kugeloberfläche ist: U = ϕ(R) =
d) C = Q/U =
ρ0 (4π/3)R3
ρ0 /(30 )R2
ρ0
R2
30
= 9.4 kV.
= 4π0 R = 55 pF.
≺./ •∞• ./
2. Zylinderkondensator
Gegeben sei ein Zylinderkondensator der Länge L = 5 cm bestehend aus zwei konzentrischen Leiterflächen. Die innere Fläche habe einen Radius a = 4.5 mm, die äußere
einen Radius b = 5 mm.
a) Bestimmen Sie die Kapazität des Kondensators mit Hilfe des Gauß’schen Satzes.
Es sei L b, so dass das elektrische Feld an den Rändern vernachlässigt werden
kann.
b) Der Kondensator wird mit Q = 1 µC geladen. Wie groß sind die Spannung zwischen den Kondensatorelektroden und die im Kondensator gespeicherte Energie?
c) Wie ändert sich die Kapazität, wenn der Zwischenraum der Leiterflächen des
Kondensators mit Glas (r = 8) gefüllt wird? (Hinweis: In Dielektrika gilt 0 wird
durch 0 · r ersetzt.)
2
J̀
^
J́
a) Wegen L b wird beim Gauss’schen Satz nur über die Manteloberfläche integriert.
Z
→
− →
−
→
−
E d A = 2π0 | E |rL
Q = 0
A
daraus erhalten wir
→
−
|E | =
Q
2π0 rL
Für die Spannung gilt
U=
Z
b
→
−
| E |dr =
a
b
Q
ln
2π0 L a
Daraus berechnet sich die Kapazität durch
C=
As
2π · 8.854 · 10−12 Vm
· 5 cm
Q
2π0 L
=
=
= 26.4 pF
5 mm
b
U
ln 4.5 mm
ln a
b) Die Spannung ist gegeben durch
U=
Q
1 µC
=
= 37.9 kV
C
26.4 pF
Die gespeicherte Energie bekommt man durch
1
1
E = CU 2 = 26.4 pF(37.9 kV)2 = 19.0 mJ
2
2
c) Durch das hinzugefügte Dielektrikum bekommt man
C=
2π0 r L
= 26.4 pF · 8 = 211.2 pF
ln ab
≺./ •∞• ./
3
C1
C2
A
d
a
d
x
3. Aufladen von zwei Kondensatoren in Reihenschaltung
Gegeben sei die dargestellte Reihenschaltung von zwei Kondensatoren mit Kapazitäten
C1 = 1 µF und C2 = 2 µF und der Erdung am rechten Ende. Am Punkt A wird die
Ladung Q = +10−6 C abgelegt.
a) Wie verteilt sich die Ladung über die beiden Kondensatoren? Geben Sie die
Ladung der Kondensatoren an.
b) Welche elektrische Spannung UA liegt am Punkt A an? Was ist der Spannungsabfall pro Kondensator?
c) Tragen Sie den Verlauf der elektrischen Spannung sowie den Verlauf der elektrischen Feldstärke über x für die Strecke zwischen Punkt A und dem Erdungspunkt
auf. Zur Bestimmung der elektrischen Feldstärke können Sie von einem Kondensatorplattenabstand d = 1 mm für beide Kondensatoren ausgehen.
J̀
^
J́
a) Bei Reihenschaltung von Kondensatoren sind die Ladungen gleich. Es gilt
Q = Cges UA = C1 U1 = C2 U2 , mit Cges = (1/C1 + 1/C2 )−1 = 0.66 µF.
Q1 = Q2 = Q = 1 µC.
b) Elektrische Spannung am Punkt A: UA = Q/Cges = 1.5 V.
Spannungen an den Kondensatoren: U1 = Q/C1 = 1 V und U2 = Q/C2 = 0.5 V.
UA = U 1 + U 2 .
c) Das elektrische
R Feld im Plattenkondensator ist homogen.
Es gilt: Ui = |Ei |dz = |Ei | · d
→ |Ei | = Ui /d.
≺./ •∞• ./
4
C1
C2
A
d
a
d
2
Spannung (V)
1
0
x
Feld (kV/m)
1
0.33
0
x
5