Parallelschaltung von Kondensatoren

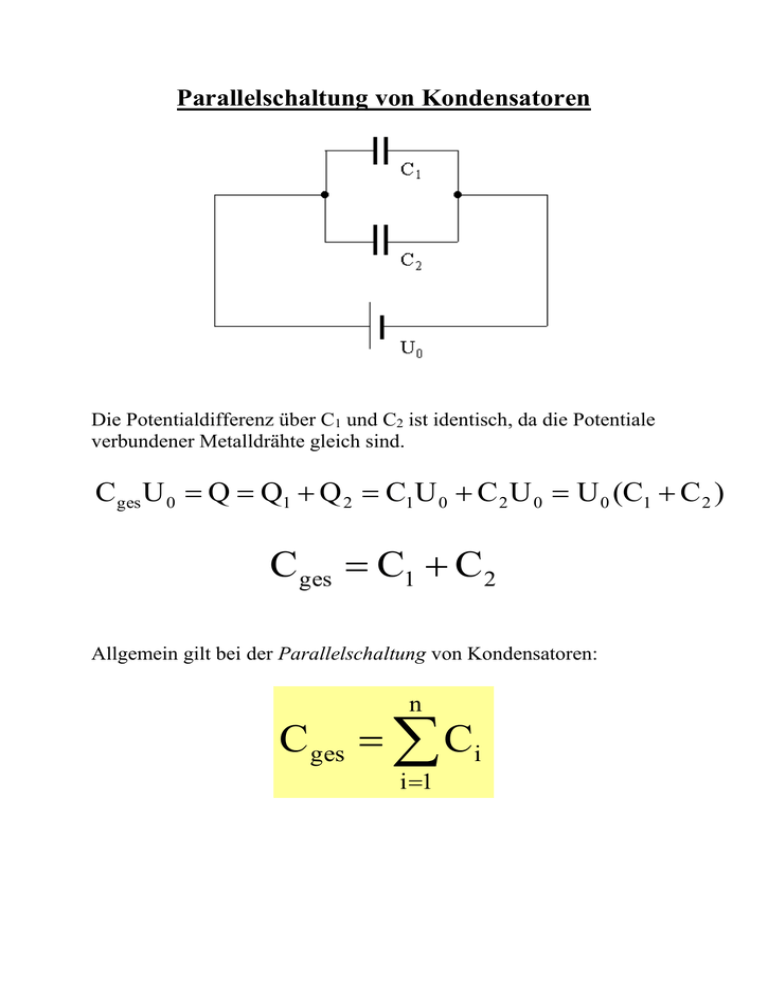
Parallelschaltung von Kondensatoren
Die Potentialdifferenz über C1 und C2 ist identisch, da die Potentiale
verbundener Metalldrähte gleich sind.
Cges U 0  Q  Q1  Q 2  C1U 0  C 2 U 0  U 0 (C1  C 2 )
C ges  C1  C 2
Allgemein gilt bei der Parallelschaltung von Kondensatoren:
n
C ges   Ci
i 1
Reihenschaltung von Kondensatoren
Die Ladungen auf den Kondensatoren C1 und C2 sind gleich groß, da
sie zwischen den Kondensatoren lediglich verschoben werden. Um
diese Verschiebung hervorzurufen, muss aus der Spannungsquelle
lediglich einmal die Ladung Q0 aufgewendet werden.
Q1  Q2  Q0
Die Gesamtspannung U0 teilt sich auf die Kondensatoren auf:
U 0  U1  U 2
Mit U=C/Q folgt daraus:
Q 0 Q1 Q 2


C ges C1 C 2
1
1
1


bzw: C
C1 C 2
ges
Allgemein gilt bei der Reihenschaltung von Kondensatoren:
n
1
1

Cges i1 Ci
Energiespeicherung im Plattenkondensators
dW  dq  u
q
u
C
  Q
A
U   Ed s   Q { 0 r }
d
C
0
d
Q
qdq 1 Q 2 1
W

 CU 2
C
2 C 2
0
(Wegen C  r gilt W  r bei U = const. und W  r-1 bei Q = const)
Mit
 0 r A 2 0 r U 2
 0 r 2
1
2
CU 
U 
(Ad ) 
E V
2
2
2 d
2 d
2
erhält man für die Energiedichte :
(unabhängig von der Geometrie des Kondensators)
1
1 
2
w   0  r E  DE
2
2
Die Energie eines geladenen Kondensators steckt im elektrischen
Feld.