1.4.1 Sozialer Überschuss

1.4 Sozialer Überschuß und potentielle Pareto-Verbesserung
Bewertung von Preissystemen und Allokationen
1.4.1 Sozialer Überschuß
Erster Schritt: "Robinson-Crusoe-Wirtschaft": Ein Konsument, ein Unternehmen, 2 Güter
In diesem Kontext bedeutet Zulässigkeit einer Allokation ( x , y ):
0 ≤ x ≤ y + ω und y ∈ Y
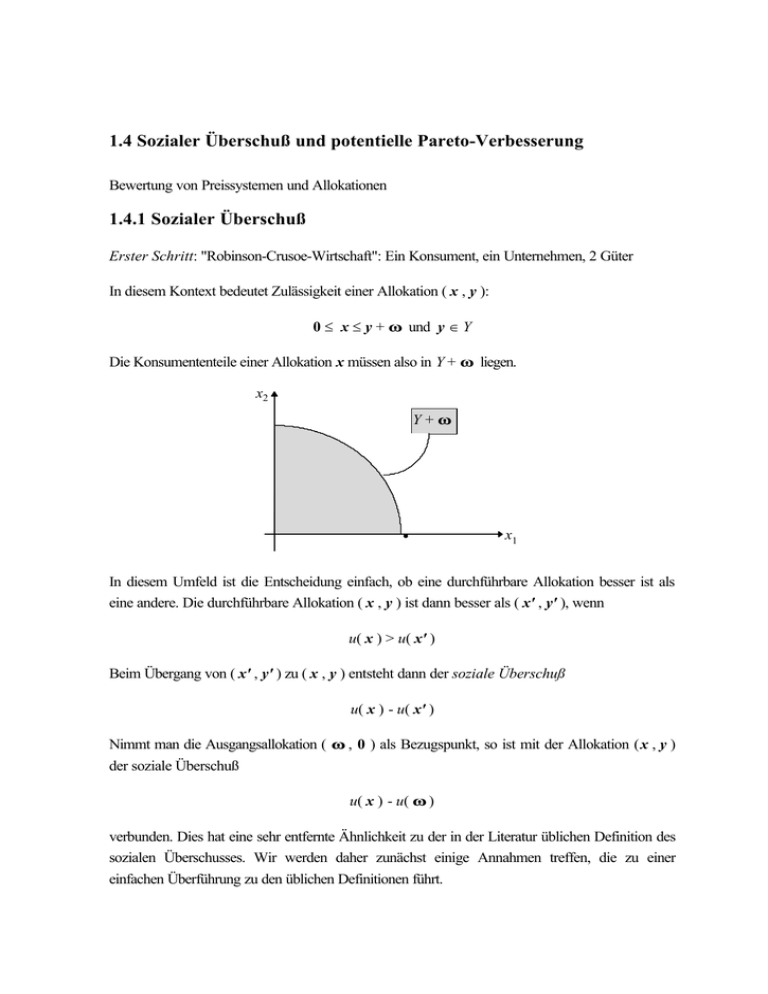
Die Konsumententeile einer Allokation x müssen also in Y + ω liegen.
x2
Y+ω
•
x1
In diesem Umfeld ist die Entscheidung einfach, ob eine durchführbare Allokation besser ist als
eine andere. Die durchführbare Allokation ( x , y ) ist dann besser als ( x' , y' ), wenn
u( x ) > u( x' )
Beim Übergang von ( x' , y' ) zu ( x , y ) entsteht dann der soziale Überschuß
u( x ) - u( x' )
Nimmt man die Ausgangsallokation ( ω , 0 ) als Bezugspunkt, so ist mit der Allokation ( x , y )
der soziale Überschuß
u( x ) - u( ω )
verbunden. Dies hat eine sehr entfernte Ähnlichkeit zu der in der Literatur üblichen Definition des
sozialen Überschusses. Wir werden daher zunächst einige Annahmen treffen, die zu einer
einfachen Überführung zu den üblichen Definitionen führt.
2
Annahmen: u( 0 ) = 0; u ist quasilinear: u( x 1, x 2 ) = x 1 + v( x 2 ), ω = ( ω1, 0 ), Y ist durch
Produktionsfunktion f gegeben: Y = { (-x, y ) | f ( x ) ≥ y, x ≥ 0 }. Wir betrachten nur
Allokationen, die technologisch effizient sind: f ( x ) = y.
Damit läßt sich der soziale Überschuß schreiben als:
u( x 1, x 2 ) - u( ω1, 0 ) = x 1 + v( x 2 ) - ω1
= -x + v( f( x ))
da die Durchführbarkeit der Allokation x 1 = -x + ω1 x 2 = y und die technologische Effizienz y =
f ( x ) fordert.
Die Funktion f -1 gibt gerade die realen Kosten der Produktion (in Einheiten von Gut 1) von y
Einheiten von Gut 2 an: C ( y ) = f -1 ( y ) = x. Damit läßt sich der Überschuß schreiben als
v( x 2 ) - C ( x 2 )
Dies legt nun natürlicherweise eine Interpretation als sozialen Überschuß nahe.
Um nun der üblichen Definition ein weiteres Stück näher zu kommen, werden wir nun auf das
Nachfrageverhalten bei quasilinearen Nutzenfunktionen eingehen:
Dazu sei das erste Gut das Numerairegut. Dann läßt sich das Nutzenmaximierungsproblem
schreiben als
max x1 + v( x 2 ) u.d.N. x1 + px2 ≤ m, x1 ≥ 0, x 2 ≥ 0
Wenn λ der Lagrangemultiplikator zur Budgetrestriktion ist, sind die Bedingungen erster Ordnung
u.a.:
1
=λ
v ' ( x2 )
=λp
also
v ' ( x2 ) = p
3
Für gegebenes p bestimmt diese Gleichung die nachgefragte Menge x 2 (die Budgetgleichung
liefert die nachgefragte Menge x 1 ). Beachte, daß x 2 unabhängig von m ist. Umgekehrt legt die
Gleichung für jede Menge x 2 den Preis p fest, zu dem diese Menge nachgefragt wird. p( x 2 ) = v '
( x 2 ) ist also die inverse Nachfragefunktion (= Preis-Absatzfunktion) für quasilineare Präferenzen.
v( x 2 ) läßt sich nun durch diese Funktion ausdrücken:
v( x 2 ) =
x2
x2
0
0
∫ v ' (x )dx = ∫ p (x )dx
p
x2
x2
Bezeichnen wir mit X2 ( p ) die Nachfrage nach Gut 2 beim Preis p, so können wir auch
schreiben:
∞
x2
v( x 2 ) =
∫ p( x )dx = ∫ X
2
( p) dp + pX 2 ( p( x2 ))
p ( x2 )
0
Der Term
∞
∫X
2
( p) dp = v( x 2 ) - pX 2 ( p( x 2 ))
p( x2 )
heißt in der Literatur Konsumentenrente. Die Konsumentenrente
∞
KR ( p ) =
∫X
2
( q) dq
p( x2 )
gibt also an, um wieviel der Nutzen des Gutes bei einem Preis p die Ausgaben übersteigt. Damit
kann man den sozialen Überschuß schreiben als:
v( X2(p) ) - C ( X2(p) ) = KR ( p ) + pX 2 ( p) - C ( X2(p) )
4
Die letzten beiden Terme sind zusammen gerade der Gewinn des Unternehmens, der in diesem
Kontext meist Produzentenrente π( p ) genannt wird. Dies ist die übliche Definition: Der soziale
Überschuß ist die Summe aus Konsumenten- und Produzentenrente.
Übung: Stellen Sie den sozialen Überschuß mit seinen Bestandteilen Konsumenten- und
Produzentenrente in einer Graphik dar, in der vertikal p und horizontal x 2 abgetragen wird.
Weisen Sie darüber hinaus nach, daß der soziale Überschuß bei der Pareto-effizienten Menge
maximal wird. Wie ist diese hier charakterisiert?
Der soziale Überschuß bezieht sich nach der obigen Argumentation auf die Bereitstellung der
Menge X2( p ) gegenüber dem Status quo x 2 = 0. Man kann aber auch den sozialen Überschuß
zweier Preissysteme (hier zweier Preise p0 und p1 für das zweite Gut) betrachten. Wenn man von
dem Preissystem p0 zum Preissystem p1 übergeht, ist damit der soziale Überschuß
KR ( p1 ) - KR ( p0 ) + π( p1 ) - π( p0 )
p0
=
∫X
2
( p )dp + π( p1 ) - π( p0 )
p1
verbunden. Falls das Ergebnis negativ ist, ist der soziale Überschuß als ein sozialer Verlust zu
interpretieren.
Als Fazit können wir festhalten, daß das Konzept des sozialen Überschusses geeignet ist, ein
Paar von Preissystemen relativ zu bewerten. Es ist daher auch ein zentrales Konzept in der
Kosten-Nutzen-Analyse von Projekten. In der obigen Situation ist das Preissystem p1 besser als
p0 , wenn der soziale Überschuß des Übergangs positiv ist und vice versa. Das Konzept hat
darüber hinaus den Vorteil, auf im Prinzip beobachtbaren Größen aufzubauen.
Bei der Entwicklung haben wir jedoch folgende Annahmen gemacht, deren Auswirkung im
folgenden zu untersuchen ist:
• Wir betrachten 2 Güter.
• Wir betrachten nur einen Konsumenten.
• Wir gehen von quasilinearen Präferenzen aus.
Die Verallgemeinerung auf mehr Güter und mehr Konsumenten ist, wie wir sehen werden, bei
quasilinearen Präferenzen nicht schwierig. Die Annahme quasilinearer Präferenzen ist jedoch
5
kritisch. Zum Schluß dieses Unterkapitels werden wir sehen, unter welchen Umständen die
Annahme kritisch ist und wann nicht.
Zweiter Schritt: Verallgemeinerung auf mehrere Güter
Der Einfachheit halber 3 Güter, mehr Güter sind aber kein Problem.
Nutzenfunktion:
u( x 1, x 2, x 3 ) = x 1 + v ( x 2, x 3 )
Das erste Gut ist immer Input für die beiden anderen Güter. Die Produktion ist charakterisiert
durch die Kostenfunktion: C ( x 2, x 3 ). Im Hinblick auf die Anwendungen, die wir betrachten
werden, ist dies eine sinnvolle Annahme.
Wir werden sofort den sozialen Überschuß, der mit einer Preisänderung verbunden ist,
betrachten. Das erste Gut wird als Numerairegut gewählt. Sei p0 = ( 1, p20, p30 ) das
ursprüngliche und p1 = ( 1, p21, p31 ) das neue Preissystem. Bei p0 fragt der Konsument
x ( p0, ω1 + π( p0 ))
nach und erreicht das Nutzenniveau
u (x ( p0, ω1 + π( p0 ))) = : V ( p0, ω1 + π( p0 )) = : u0
und analog bei p1
u (x ( p1, ω1 + π( p1 ))) = : V ( p1, ω1 + π( p1 )) = : u1
Aufgrund der Quasilinearität der Präferenzen gilt für ( p, m ) mit x ( p, m ) > 0:
V ( p, m ) = v ( p ) - p2 x 2 ( p, ) - p3 x 3 ( p ) + m
mit v ( p ) = v ( x 2 ( p ), x 3 ( p ) ). Man beachte, daß x i ( p ) für i = 2, 3 nicht von m echt
abhängen (Warum?).
Der soziale Überschuß des Übergangs von p0 nach p1 läßt sich dann schreiben:
6
V ( p1, ω1 + π( p1 )) - V ( p0, ω1 + π( p0 ))
= v ( p1 ) - p2 x 2 ( p1 ) - p3 x 3 ( p1 ) + ω1 + π( p1 )
- [ v ( p0 ) - p2 x 2 ( p0 ) - p3 x 3 ( p0 ) + ω1 + π( p0 ) ]
Um zu den üblichen Definitionen zu gelangen, ist es nützlich, zunächst die folgende Definition der
kompensierenden Variation (compensating variation) zu besprechen. Dazu sei u1 > u0 . Die
definierende Frage ist: Wieviel können wir von dem Einkommen des Konsumenten bei p1 , ω1 +
π( p1 ), abziehen, so daß der Konsument sich gerade so gut stellt, wie in der alten Situation p0 ?
Diesen Betrag nennen wir kompensierende Variation, CV, und dieser ist durch
V ( p1, ω1 + π( p1 ) - CV ) = V ( p0, ω1 + π( p0 )) = u0
definiert. Man beachte, daß die kompensierende Variation im Fall quasilinearer Präferenzen mit
dem sozialen Überschuß übereinstimmt:
V ( p1, ω1 + π( p1 )) - V ( p0, ω1 + π( p0 ))
= V ( p1, ω1 + π( p1 )) - V ( p1, ω1 + π( p1 ) - CV )
= v ( p1 ) - p2 x 2 ( p1 ) - p3 x 3 ( p1 ) + ω1 + π( p1 )
- [ v ( p1 ) - p2 x 2 ( p1 ) - p3 x 3 ( p1 ) + ω1 + π( p1 ) - CV ]
= CV
Wenn wir also wissen, wie man die kompensierende Variation bestimmen können, wissen wir
dies auch für den sozialen Überschuß. Dazu also jetzt:
Sowohl beim Einkommen ω1 + π( p0 ) und dem Preissystem p0 als auch beim Einkommen ω1 +
π( p1 ) - CV und dem Preis p1 erreicht der Konsument das Nutzenniveau u0. Daraus folgt, daß er
beim Vorliegen von p0 die Aufwendungen ω1 + π( p0 ) = : e ( p0, u0) tätigen muß, um u0 zu
erreichen; und daß er beim Vorliegen von p1 die Aufwendungen ω1 + π( p1 ) - CV = : e ( p1, u0)
tätigen muß. e ( p, u) bezeichnet den Wert der sogenannten Ausgabenfunktion, die aus der
Mikroökonomik bekannt sein müßte (falls nicht, z.B. Varian konsultieren!). Daraus folgt:
CV = ω1 + π( p1 ) - e ( p1, u0) = e ( p0, u0) - π( p0 ) + π( p1 ) - e ( p1, u0)
7
= π( p1 ) - π( p0 ) + e ( p0, u0) - e ( p1, u0)
Der soziale Überschuß ist also gleich der Änderung der Produzentenrente und der
Ausgabenänderungen. Der letzte Schritt, der den Zusammenhang zwischen Ausgabenänderung
und Konsumentenrentenänderungen herstellt, folgt nun sehr schnell aus der Eigenschaft der
Ausgabenfunktion:
∂e
( p, u) = hi ( p, u)
∂pi
wobei hi ( . , . ) die kompensierte (oder Hicks' sche) Nachfragefunktion bezeichnet. Die
Annahme, daß wir quasilineare Präferenzen angenommen haben, bewirkt nun erstens, daß hi nicht
von u abhängt, und zweitens, daß hi mit der üblichen (Marshall' schen) Nachfragefunktion
hi ( p ) = x i ( p ) . Also haben wir:
∂e
( p, u) = xi ( p)
∂pi
Dies ermöglicht nun die Darstellung der Ausgabenänderung
Integraldarstellungen über die Nachfragefunktionen:
durch
die
üblichen
e ( p0, u0) - e ( p1, u0)= e ( p20, p30, u0) - e ( p21, p30, u0)
+ e ( p21, p30, u0) - e ( p21, p31, u0)
p20
p30
∂e
∂e 1
= ∫
( p2 , p 30 , u 0 ) dp2 + ∫
( p 2 , p3 , u 0 )dp 3
p12 ∂p2
p13 ∂p3
p20
=
∫x
p
1
2
2
( p 2 , p30 )dp 2 +
p30
∫ x (p ,p
3
1
2
3
) dp3
p
1
3
Der erste Term ist nun die Konsumentenrente des Übergangs von p20 nach p21 und der zweite die
Konsumentenrente des Übergangs von p30 nach p31 . Allgemein kann man also bei quasilinearen
Präferenzen die Konsumentenrente, die mit dem Übergang vom Preis-system p0 zum Preissystem
p1 verbunden ist, in die Summe der Konsumentenrenten, die mit den einzelnen Preisänderungen
verbunden sind, aufspalten.
Dritter Schritt: Verallgemeinerung auf mehrere Konsumenten
8
Der Einfachheit halber gehen wir wieder auf den 2-Güterfall zurück. Außerdem werden wir hier
sehr heuristisch vorgehen und erst in 1.4.2 sehen, daß sich diese Vorgehensweise formal
Im ersten Schritt haben wir den sozialen Überschuß zunächst als Nutzensteigerung eines
Konsumenten gemessen. Es ist naheliegend, den sozialen Überschuß bei mehreren Konsumenten
als Summe der einzelnen Nutzenänderungen zu definieren. Dies werden wir hier in der Tat tun:
Wir definieren den sozialen Überschuß als Summe von Änderungen der Produzentenrente und
der Summe der Nutzenänderungen. Dies führt analog zum ersten Schritt zu:
n p0
π ( p1 ) - π ( p0 ) +
∑ ∫x
=
2k
( p )dp
k 1p
1
wobei x 2k die Nachfrage des Konsumenten k nach dem zweiten Gut bezeichnet. Da aber
n p0
∑ ∫x
=
2k
k 1p
1
( p) dp =
p0 n
∫ ∑= x
p0
2k
( p) dp =
p k 1
1
∫x
2
( p )dp
1
p
wobei x 2 die aggregrierte Nachfrage nach Gut 2 bezeichnet. Damit läßt sich der soziale
p0
π ( p1 ) - π ( p0 ) +
∫x
2
( p) dp
1
p
Dies ist die in der Literatur übliche Darstellung des sozialen Überschusses als Summe von
Produzenten- und Konsumentenrente.
Offen bleibt hier, inwieweit die Annahme der Quasilinearität eingeht (dazu gleich im Anschluß)
und inwieweit das Maß einer Summe von Nutzen sinnvoll ist (dazu in 1.4.2).
Vierter Schritt: Die Annahme der Quasilinearität
Um einen Eindruck zu gewinnen, beschränken wir uns auf eine Welt mit zwei Gütern ohne
Produktion und nur einem Konsumenten. Wir betrachten wieder den Übergang vom Preissystem
p0 = ( 1, p20) zum Preissystem p1 = ( 1, p21). Damit erreicht der Konsument den Nutzen V( p0,
m) = u0 bzw. V( p1, m) = u1. Der Nutzenüberschuß ist also
u1 - u0 = V( p1, m) - V( p0, m)
9
Wie oben läßt sich die kompensierende Variation CV über
V( p1, m - CV) = u0
definieren. Damit wird der Nutzenüberschuß
V( p1, m) - V( p1, m - CV)
Nach dem Mittelwertsatz der Differentialrechnung gibt es daher ein Einkommen m* ∈ [ m - CV,
m ], so daß
V( p1, m) - V( p1, m - CV) =
∂V 1
( p , m*) CV
∂m
∂V 1
( p , m*) = 1. Dies ist der erste wichtige
∂m
Unterschied. Die kompensierende Variation ist i.a. nicht gleich dem Nutzenüberschuß. Der zweite
Unterschied ergibt sich durch den Zusammenhang zwischen CV und der Nachfragefunktion. Wie
oben läßt sich zunächst CV ausdrücken als
gilt. Bei quasilinearen Nutzenfunktionen ist
CV = e ( p0, u0 ) - e ( p1, u0 )
und dies ist wiederum darstellbar durch
p0
CV = ∫ h2 ( p) dp
p1
I.a. gilt nun aber keineswegs hi( p, u ) = x i( p, m ) für ein Intervall von Preisen. Natürlich gilt für
p = p0:
h2( p0, u0 ) = h2( p0, V ( p0, m )) = x 2( p0, m )
Für andere Preise gilt dies jedoch i.a. nicht, wie man sich schnell mit Hilfe der Slutzky-Gleichung
klarmacht.
∂x2 0
∂h
∂x
( p , m) = 2 ( p 0 , u 0 ) − x 2 ( p 0 , m) 2 ( p 0 , m)
∂p
∂p
∂m
Wenn das zweite Gut ein normales Gut ist, fällt die übliche (Marshall'sche) Nachfragefunktion
stärker im eigenen Preis als die Hicks'sche Nachfragefunktion. Also scheitert i.a. auch die
Darstellung der CV durch die beobachtbare Nachfragefunktion.
10
Wir sehen also, daß die Annahme der Quasilinearität zentral für die übliche Darstellung des
sozialen Überschusses ist. Wie groß ist der "Fehler", wenn man dieses Maß trotzdem benutzt?
Quasilineare Nutzenfunktionen führen zu verschwindenden Einkommenseffekten. Umgekehrt
kann man nachweisen, daß Einkommenseffekte nur verschwinden, wenn die Präferenzen
quasilinear sind. Einkommenseffekte sind demnach ein Indiz, ob die Annahme der Quasilinearität
kritisch ist oder nicht. Wenn wir Güter betrachten, bei denen die Einkommenseffekte stark sind,
schränkt die Annahme der Quasilinearität die Anwendung relativ stark ein. Falls wir jedoch Güter
betrachten, bei denen die Güternachfrage wenig einkommensabhängig ist, können wir mit dieser
Annahme approximativ gut arbeiten. Zu der Relevanz der Maße von sozialen Überschüssen vgl.
Willig, R. (1976): Consumer's Surplus without Apology, American Economic Review 66, S.
589-587.