Vorkurs Grundlagen für das Mathematikstudium Lösungen 1

Universität Zürich, 12. September 2011
Vorkurs Grundlagen für das Mathematikstudium
Lösungen 1: Algebra und Logik
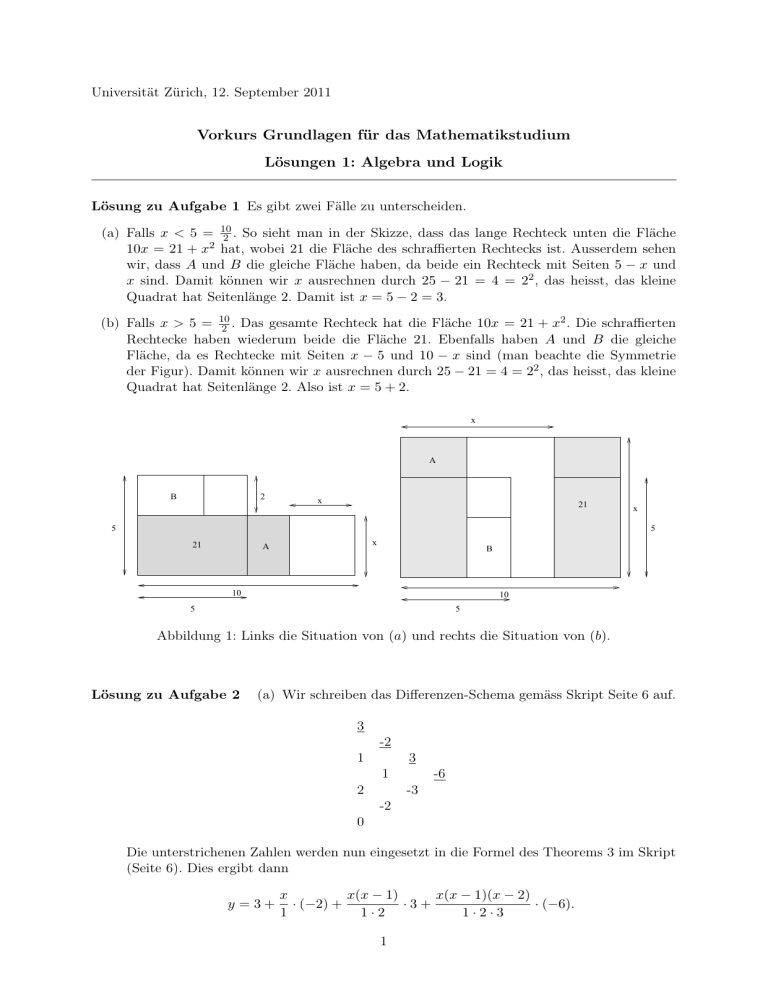
Lösung zu Aufgabe 1 Es gibt zwei Fälle zu unterscheiden.
(a) Falls x < 5 = 10
2 . So sieht man in der Skizze, dass das lange Rechteck unten die Fläche
10x = 21 + x2 hat, wobei 21 die Fläche des schraffierten Rechtecks ist. Ausserdem sehen
wir, dass A und B die gleiche Fläche haben, da beide ein Rechteck mit Seiten 5 − x und
x sind. Damit können wir x ausrechnen durch 25 − 21 = 4 = 22 , das heisst, das kleine
Quadrat hat Seitenlänge 2. Damit ist x = 5 − 2 = 3.
2
(b) Falls x > 5 = 10
2 . Das gesamte Rechteck hat die Fläche 10x = 21 + x . Die schraffierten
Rechtecke haben wiederum beide die Fläche 21. Ebenfalls haben A und B die gleiche
Fläche, da es Rechtecke mit Seiten x − 5 und 10 − x sind (man beachte die Symmetrie
der Figur). Damit können wir x ausrechnen durch 25 − 21 = 4 = 22 , das heisst, das kleine
Quadrat hat Seitenlänge 2. Also ist x = 5 + 2.
x
A
B
2
x
21
x
5
5
21
x
A
B
10
10
5
5
Abbildung 1: Links die Situation von (a) und rechts die Situation von (b).
Lösung zu Aufgabe 2
(a) Wir schreiben das Differenzen-Schema gemäss Skript Seite 6 auf.
3
-2
1
3
1
2
-6
-3
-2
0
Die unterstrichenen Zahlen werden nun eingesetzt in die Formel des Theorems 3 im Skript
(Seite 6). Dies ergibt dann
y =3+
x
x(x − 1)
x(x − 1)(x − 2)
· (−2) +
·3+
· (−6).
1
1·2
1·2·3
1
Multiplizieren wir aus und gruppieren die Terme gleicher Potenz, so erhalten wir schliesslich
das Polynom vom Grad 3: y = −x3 + 29 x2 − 11
2 x + 3. Durch Einsetzen kann man sich davon
überzeugen, dass die Punkte P , Q, R und S wirklich im Graphen des Polynoms liegen.
(b) Hier wissen wir nicht, welchen Grad das gesuchte Polynom hat. Wir betrachten das DifferenzenSchema.
0
1
13
7
23
13
+
23
12
19
6
33
13 + 23 + 33
18
37
43
13 + 23 + 33 + 43
0
6
24
61
0
0
6
Diese Form legt die Vermutung nahe, dass das Polynom den Grad 4 haben muss, da nachher
die Einträge im Differenzenschema 0 sind. Wir haben das natürlich nur für wenige Zeilen
überprüft. Daher argumentieren wir nun allgemein. Die Einträge in der zweiten Spalte sind
jeweils n3 . Die Einträge in der dritten Spalte sind
(n + 1)3 − n3 = 3n2 + 3n + 1.
Die Einträge in der vierten Spalte sind
3(n + 1)2 + 3(n + 1) + 1 − 3n2 − 3n − 1 = 6(n + 1).
Die Einträge in der fünften sind schliesslich immer 6 und in der sechsten (und damit in
allen darauf folgenden Spalten) immer 0. Es sind also nur fünf Spalten nicht 0 (wobei die
ersten Spalte einfach der Funktionswert ist). Also hat das Polynom tatsächlich Grad 4.
Setzen wir die Zahlen in die Formel ein (wie in (a)), so ergibt dies
x(x − 1)(x − 2)
x(x − 1)(x − 2)(x − 3)
x(x − 1)
+ 12 ·
+6·
2
6
24
4
3
2
x
x
x
+
+ .
4
2
2
y = x+7·
=
Wir können wiederum einsetzen, um zu sehen, dass das Polynom an den entsprechenden
Stellen die gewünschten Werte annimmt.
Lösung zu Aufgabe 3 (a) Das Verfahren mit Theorem 3 liefert ein Polynom von Grad 3,
das vorgegebene Werte an den Stellen 0, 1, 2 und 3 annimmt. In der Aufgabe sind nur
die Werte für 1, 2 und 3 vorgegeben. Wir können also zwei unterschliedliche Werte an der
Stelle 0 vorgeben und erhalten zwei unterschiedliche Polynome (denn sie unterscheiden sich
ja an der Stelle 0!).
(b) Wir betrachten das Differenzen-Schema mit den ersten 4 Werten.
-1
3
2
2
5
7
6
8
13
20
2
Setzen wir die unterstrichenen Zahlen in die Formel ein, so erhalten wir
y = −1 + 3x + 2 ·
x(x − 1)
x(x − 1)(x − 2)
+6·
= x3 − 2x2 + 4x − 1.
2
6
Setzen wir nun in diese Formel x = 4 ein, so ergibt dies 47. Damit gibt es kein Polynom vom
Grad 3 mit den gewünschten Eigenschaften.
Lösung zu Aufgabe 4
(a) Nein, denn das Niesen der Katze ist nur notwendig, nicht aber hinreichend für den Regen.
Achtung: falsche Schlussrichtung! Eine Schwierigkeit dabei ist, dass die kausale Abfolge
nicht der zeitlichen entspricht.
(b) Ja. Heute ist der 1. Januar. Dann war vorgestern der 30. Dezemeber, Peter hatte am 31.
Dezember letzten Jahres seinen 11. Geburtstag. Somit wird er am 31. Dezember nächsten
Jahres 13.
Lösung zu Aufgabe 5 Wir wissen mit Sicherheit, dass mindestens jemand kommt, nämlich
Walter oder Kathrin. Wir betrachten diese beiden Fälle einzeln.
• Kommt Walter, so kommen auch Kathrin und Herr Meier. Mit Herr Meier kommt aber
auch Frau Meier. Da Kathrin kommt, ist auch Franziska dabei. Daraus folgt, dass in diesem
Falle die ganze Familie kommt. Das steht also im Widerspruch dazu, dass Frau Meier und
Franziska keinesfalls zusammen kommen. Somit kann dieser Fall nicht eintreten.
• Kommt Kathrin, so kommt sicherlich auch Franziska. Dann aber kann Frau Meier nicht
kommen und daher auch Herr Meier nicht (denn er geht nicht ohne sie). Im ersten Schritt
haben wir schon ausgeschlossen, dass Walter kommt. Somit ist klar, dass nur die beiden
Töchter kommen.
Lösung zu Aufgabe 6
(a)
(i) Ist eine Aussage, die falsch ist.
(ii) Ist ein Befehl. Dieser kann nicht wahr oder falsch sein, daher ist es keine Aussage.
(iii) Ist keine Aussage. Denn wäre der Satz wahr, so sage ich nicht die Wahrheit. Dann aber
ist der Satz nicht wahr. Wäre der Satz andererseits falsch, so sage ich die Wahrheit,
also ist der Satz wahr. Dies führt nun aber dazu, dass der Satz wahr und falsch sein
müsste. Das kann jedoch nicht sein. Daher ist der Satz keine Aussage.
(b)
(i) Es gibt mindestens eine Frau, die nicht schön ist.
(ii) Der Boden ist nicht nass vom Regen und es gibt niemanden, der den Boden mit dem
Wasserschlauch vollgespritzt hat. Deutsch: Der Boden ist weder vom Regen nass noch
hat ihn jemand mit dem Wasserschlauch vollgespritzt.
(iii) Es gibt mindestens eine Frau oder einen Mann, die oder der immer alles vom Teller
aufgegessen hat.
Lösung zu Aufgabe 7 Das Problem liegt im Induktionsschluss. Ist nämlich M 0 = {b, d}, so
haben wir (M 0 \ {b}) ∩ (M 0 \ {d}) = ∅. Dann aber lässt sich die Transitivität der Gleichheit nicht
mehr anwenden.
Lösung zu Aufgabe 8
(a) Induktionsanfang: Sei n = 0. Dann gilt
für n = 0.
Pn
k=0 k
3
=0=
0(0+1)
.
2
Somit ist die Aussage richtig
Induktionsschluss: Wir nehmen an, die Aussage sei richtig für n und wollen zeigen, dass
sie dann auch für (n + 1) richtig ist. Dazu schreiben wir
n+1
X
k=
k=0
n
X
k + (n + 1).
k=0
Auf den ersten Summanden können wir nun die Induktionsannahme anwenden und
erhalten
n+1
X
n(n + 1)
(n + 1)(n + 2)
k=
+ (n + 1) =
.
2
2
k=0
Dies beendet den Induktionsschluss.
P
(b) Induktionsanfang: Sei n = 0. Dann gilt nk=0 k 2 = 02 =
richtig für n = 0.
0(0+1)(2·0+1)
.
6
Somit ist die Aussage
Induktionsschluss: Wir nehmen an, die Aussage sei richtig für n und wollen zeigen, dass
sie dann auch für (n + 1) richtig ist. Dazu schreiben wir
n+1
X
2
k =
k=0
n
X
k 2 + (n + 1)2 .
k=0
Auf den ersten Summanden können wir nun die Induktionsannahme anwenden und
erhalten
n+1
X
k2 =
k=0
=
=
=
n(n + 1)(2n + 1)
+ (n + 1)2
6
n(n + 1)(2n + 1) + 6(n + 1)2
6
2
(n + 1)(2n + 7n + 6)
6
(n + 1)(n + 2)(2n + 3)
.
6
Dies beendet den Induktionsschluss.
Lösung zu Aufgabe 9
(a) Da (n + 1)! gerade das Produkt der Zahlen 2, . . . , (n + 1) ist, kann man jeweils den zweiten
Summanden ausklammern, was dann beweist, dass es keine Primzahlen sein können. So ist
zum Beispiel (n + 1)! + 3 = 3(2 · 4 · · · (n + 1) + 1).
(b) Sei also {p0 , . . . , pm } die Menge aller Primzahlen. Dann definieren wir
q := p0 · · · pm + 1.
Jede natürliche Zahl besitzt eine eindeutige Zerlegung in Primfaktoren. Aber teilen wir q
durch eine beliebige Primzahl pi , so erhalten wir Rest 1. Das bedeutet, dass q nicht weiter
zerlegt werden kann und somit selbst eine Primzahl ist. Dies jedoch ist ein Widerspruch,
denn q ist nicht in der Menge aller Primzahlen enthalten. Wir können also folgern, dass es
unendlich viele Primzahlen gibt.
Bemerkung: In der obigen Argumentation verwenden wir, dass es Primzahlen gibt. Wäre
nämlich die Menge der Primzahlen leer, so wäre q = 1, also keine Primzahl.
4