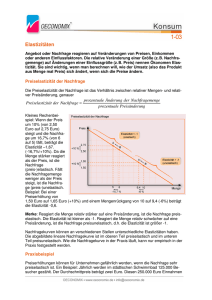
Preiselastizität der Nachfrage

2-72 –
2.8.2.5
Fabianca
BWL III – A – Marketing
Sonstige Faktoren
Es gibt noch eine Reihe weiterer Einflussfaktoren, die bei der Preisfestsetzung beachtet werden
sollten:

Hier sind zunächst psychologische Auswirkungen von Preisen zu beachten. Diese wirken
wesentlich auf die Nachfrager ein, teilweise aber auch auf Wettbewerber und ggf. auf den
Handel. So liegen die Preise oftmals entweder unterhalb von Preisschwellen wie 1 €, 10 € etc.
Muss der Preis eines Produktes z.B. aufgrund gestiegener Unternehmenskosten über eine
solche Preisschwelle gehoben werden, wird er meist deutlich über die Preisschwelle gehoben.
Aus 9,99 € werden dann z.B. 10,49 €.
Manchmal kann man das Phänomen beobachten, dass ein Produkt zu einem höheren Preis
sogar häufiger gekauft wird als zu einem niedrigeren Preis. Hierbei spielt eine Rolle, dass der
Preis eines Produktes von vielen Kunden als Qualitätsindikator herangezogen wird und entsprechend ein höherer Preis als Hinweis auf eine hohe Produktqualität gewertet wird.

Selbstverständlich müssen bei der Preisfestlegung auch die preispolitischen Zielsetzungen
des Unternehmens berücksichtigt werden. Diese limitieren den Spielraum der Preise und
schließen unter Umständen das Angebot besonders preiswerter oder teurer Produkte aus.

In einigen Märkten haben schließlich Gesetzesvorschriften Relevanz für die Preispolitik (z.B.
Buchpreisbindung, Märkte mit hohen Steuerlasten wie Tabakwaren oder Alkoholika) und müssen bei der Preisfestlegung Berücksichtigung finden. Für alle Märkte außer dem Buchhandel
gilt in Deutschland im Übrigen das Verbot der Preisbindung.
2.8.3 Die Preiselastizität der Nachfrage
Für preispolitische Maßnahmen von Unternehmen genügt es oft nicht, zu wissen, dass die nachgefragte Menge eines Gutes grundsätzlich von der Höhe des Preises, vom Einkommen der Haushalte und anderen Faktoren abhängt. Als Entscheidungsgrundlage sind vielmehr häufig Informationen
darüber wichtig, in welchem Ausmaß sich die Gesamtnachfrage nach einem Gut ändert, wenn sich
beispielsweise der Preis oder das Einkommen ändert. Eine Maßzahl für das Ausmaß einer solchen
Änderung ist die Elastizität:
Die Elastizität gibt an, um wie viel Prozent sich eine abhängige (= reagierende) Größe ändert,
wenn sich die unabhängige (= verursachende) Größe um 1 % ändert.
Mit Hilfe der Preiselastizität versucht man also, den Zusammenhang zwischen der Nachfragemenge und dem Preis zu konkretisieren. Man spricht von einer

elastischen Nachfrage, wenn sich eine Preisänderung stark auf die nachgefragte Menge
auswirkt und von einer

unelastischen Nachfrage, wenn eine Preisänderung die nachgefragte Menge nur wenig
verändert.
Beispiel:
Eine Preiserhöhung für einen bestimmten Autotyp von 40.000 € um 200 € auf 40.200 € wird die
nachgefragte Menge kaum beeinflussen, die Nachfrage ist demnach bei dieser Preiserhöhung
unelastisch. Wird dagegen der Preis eines Mountainbikes ebenfalls um 200 € von bisher 400 € auf
jetzt 600 € erhöht, wird die nachgefragte Menge spürbar sinken. Diese Nachfrage ist also elastisch.
Aus dieser Beobachtung lässt sich aber nicht schließen, dass bei beliebigen Preisänderungen die
Nachfrager nach Autos weniger stark reagieren als die Nachfrager nach Mountainbikes. Der Preis
für das Auto wurde nur um1%, der Preis für das Mountainbike dagegen um 50 % erhöht. Bei einer
Erhöhung des Autopreises um 50% würde die nachgefragte Menge bei Autos ebenfalls stark zurückgehen, die Nachfrage wäre dann ebenfalls elastisch.
2.8.3.1
(Direkte) Preiselastizität der Nachfrage
Die direkte Preiselastizität der Nachfrage misst, wie sich eine Preisänderung eines Gutes auf die
nachgefragte Menge und damit auf dem Umsatz dieses Produktes auswirkt. Sie ist das Verhältnis
zwischen der prozentualen Änderung der nachgefragten Menge eines Gutes zur prozentualen
Fabianca
BWL III – A
– Marketting – 2-73
Prreisänderung
g dieses Gutes und gibt a
an, um wie viel
v Prozent sich
s
die nachhgefragte Me
enge eines
Gutes ändert, wenn sich der Preis diesses Gutes um
m 1 % ändert.
Diie Preiselastizität der Nac
chfrage kann
n durch folge
ende Formel berechnet w
werden:
x  100
x1
prozentuale Änderung
g der Nachfra
agemenge
x P1 x1  x 2 P1






P  100 P x1 P1  P2 x1
prrozentuale Pr eisänderun
ng
P1
Man bezeichnet diese Elas
stizität auch als Bogenelastizität.
Ess gilt:

hfrage elastiisch, d.h. die
e prozentuale
e Änderung der Nachfrag
ge ist größerr
Ist ε < -1, ist die Nach
als die prrozentuale Än
nderung dess Preises. Ein
ne starke Reaktion der N
Nachfrage auf Preisveränderung
gen zeigt sich
h beispielswe
eise bei gute
en Substituten wie etwa S
Schrauben oder Nägel
ise fast alle Kunden zur
einer besstimmten Sorrte. Wird der Preis erhöhtt, wechseln möglicherwe
m
Konkurrenz, wird der Preis verring
gert, wechse
eln die Kunde
en wieder zurrück. Eine Preiserhöhung verkkleinert die Gesamteinna
G
ahmen, währrend eine Pre
eissenkung zzu einer Ums
satzsteigerung führtt.

Ist -1 > ε < 0, ist die Nachfrage
N
u
unelastisch, d.h. die proz
zentuale Ändderung der Nachfrage
N
ist
kleiner alss die prozentuale Änderu
ung des Preises. Eine schwache Reaaktion der Na
achfrage auf
Preisverä
änderungen zeigt
z
sich be
esonders bei lebensnotwe
endigen Wirttschaftsgüterrn wie Nahrungsmitttel, die schlec
cht substituie
ert werden können. Eine Preiserhöhuung vergröße
ert also den
Erlös, wä
ährend eine Preissenkung
P
g die Einnahmen verklein
nert.

Ist ε = -1, spricht man
n von einer p
proportionale
en Elastizitä
ät. Dann ist ddie prozentua
ale Änderung der Nachfrage genau so groß
ß wie die pro
ozentuale Än
nderung des Preises. In diesem
d
Fall
bleibt derr Umsatz kon
nstant.
2-74 –
Fa
Fabianca
BW
WL III – A – Marketing

Ist ε = 1, ist die Nacchfrage völliig unelastis ch. Auch ein
ne maximale Preisänderuung bewirkt
keine M
Mengenände
erung. Dies is
st z.B. bei leb
benswichtige
en Medikame
enten (z.B. Innsulin) oder
Sammllerstücken (zz.B. Briefmarrken) der Falll.

Ist ε > 1, spricht ma
an von einer anormalen Elastizität, einer inversen Elastizitäät oder einerr
positiv
ven Elastizittät. Dabei ind
duziert ein hö
öherer Preis eine höhere
e Nachfrage. In diesem Fall
F
sprichtt man auch von
v superiorren Gütern ((meist auch als
a Luxusgüter bezeichneet). Dies ist
beispie
elsweise der Fall, wenn mit
m steigende
em Preis eine
e zunehmend
de Exklusivittät des Gutes
s
assoziiiert wird (Sno
obeffekt, de
emonstrative
er Konsum) oder wenn aus
a der Erhööhung des
Preisess auf eine be
evorstehende
e Verknappu
ung des Gute
es geschlossen wird (Ham
msterkauf).
Bei Ha
aushalten, die
e am Existen
nzminimum le
eben, findet man die sog. Giffen-Güttern (absolu
ut
inferio
oren Gütern),
) die ebenfalls eine inverrsen Elastizittät aufweisen
n. Beispiel: JJemand hat
3 Euro am Tag zur Verfügung. Er kauft jede
en Tag 1 Laib
b Brot für 1 Euro
E
und 1 S
Stück Fleisch
h
für 2 Euro. Jetzt ste
eigt der Brotp
preis auf 1,5 0 Euro. Da er
e nach einem
m Laib Brot nnicht mehr genug Ge
eld für Fleiscch übrig hat, kauft er statttdessen eine
en weiteren Laib
L
Brot.
Die Pre
eiselastizität der Nachfrage eines besstimmten Gu
utes kann alle
erdings nichtt für jedes
Preisniiveau positivv sein; dies würde
w
das Vo
orhandensein
n unendlicher finanziellerr Mittel bei de
en
Nachfrragern erfordern. Der Bro
otpreis steigt weiter auf 2 Euro. Derjen
nige, der nurr 3 Euro am
Tag zu
ur Verfügung hat, kann sich nunmehr nur noch 1,5
5 Laibe Brot pro Tag leistten.
Fabianca
2..8.3.2
BWL III – A
– Marketting – 2-75
Be
eispiel zurr Elastizitä
ätsberechnung
An
ngenommen, ein Lebens
smittelmarkt h
hat für eine bestimmte
b
Sorte Frischm
milch einen Zu
usammenha
ang zwischen
n der tägliche
en Absatzme
enge und dem Preis festg
gestellt, wie er in der folg
genden linearren Nachfrag
gekurve zum Ausdruck ko
ommt:
g um 0,25 € von 1,00 € auf
W
Wie Sie sehen
n, führt eine Preissenkun
P
a 0,75 € (d .h. eine Preisänderung
vo
on –25%) zu einer Nachfrrageerhöhun
ng von 40 au
uf 80 Liter (d.h. eine Absaatzsteigerung
g um
+1
100%). Die Preiselastizitä
P
ät der Nachfrrage beträgt
x  x 2 P1 40  80 1

 1

 4 ,

P1  P2 x1 1  0,75 40
d.h. die Nachffrage ist stark
k elastisch.
Alternativ könn
nte man die Elastizität au
uch über die Prozentzahlen berechneen:
prozentuale Nachfrage
eänderung 100


 4
25
prozentuale Pr eisän
nderung
La
ag der Umsa
atz vor der Prreisänderung
g bei Ualt = Palt  xalt = 1  40 = 40 €, liiegt er nach der Preisse
enkung bei Uneu = Pneu  xneu = 0,75  80 = 60 €, d.h. der Umsa
atz ist um 500 % gestiegen.
W
Würde man be
ei einem Aus
sgangspreis vvon 0,50 € den
d Preis noc
chmals um 00,25 € senken
n, ergäbe
da
as eine Nach
hfragesteigerrung von 120
0 auf 160 Lite
er. Dann läge
e die Elastiziität bei
x  x 2 P1 120  160
0 0,5

 1

 0,,66 ,

P1  P2 x1 0,5  0,25
5 120
h wenn die absoluten
d.h. die Nachffrage ist unelastisch, auch
a
Pre
eis- und Menngenänderun
ngen identissch sind.
La
ag der Umsa
atz vor der Prreisänderung
g bei Ualt = Palt  xalt = 0,5  120 = 60 €€, liegt er nach der
Prreissenkung bei Uneu = Pneu  xneu = 0 ,25  160 = 40
4 €, d.h. der Umsatz ist um 50 % ge
esunken.
Da
as Zahlenbeispiel zeigt, dass
d
die dire
ekte Preiselastizität der Nachfrage
N
trootz gleicher absoluter
a
Prreis- und Mengenänderungen und lin
nearer Nachfrragefunktion in beiden Fäällen verschiieden ist.
Istt die prozenttuale Änderu
ung der nach gefragten Menge genaus
so hoch wie die prozentu
uale Preisän
nderung, so hat die Elastizität den W
Wert 1. Das trrifft hier für de
en Halbierunngspunkt derr Nachfrageku
urve zu (Punkt B).
2-76 –
Fabianca
2.8.3.3
BWL III – A – Marketing
Punkt- und Bogenelastizität
Alle bisher betrachteten Elastizitäten waren sog. Bogenelastizitäten der Nachfrage, denn wir sind
immer von zwei Punkten auf der Nachfragekurve ausgegangen. Bei „kleinen“ Preis-MengenÄnderungen liefert diese Form der Elastizitäten einen guten Näherungswert. Die Bogenelastizität
hat die Eigenschaft, dass sie bei einer Preissenkung von P1 auf P2 genau so groß ist wie bei einer
Preissteigerung von P2 auf P1.
Will man jedoch den exakten Wert der Elastizität in einem Punkt bestimmen, benötigt man die
sog. Punktelastizität der Nachfrage. Sie ist definiert als das Verhältnis der relativen Änderung der
Nachfrage nach einem Gut zu der sie auslösenden relativen Preisänderung für dieses Gut in einem
infinitesimal kleinen Bereich. Zur Berechnung der (relativen) Punktelastizität kann man folgende
Formel benutzen:

  (x) 
dx P
P
  x '(P) 
dP x
x
Beispiel 1:
Für die Preis-Absatz-Funktion x(P) 
10
ergibt sich die Punktelastizität
P

P
10 P
10
 2 
.
x
Px
P x

10
10
1

 1 .
Im Punkt x   10 beträgt damit die direkte Punktelastizität   
Px
10  1
P

10
10
2
Im Punkt x   5 beträgt damit die direkte Punktelastizität   

 1 .
Px
52
P
Damit handelt es sich bei dieser Funktion um einen Sonderfall mit konstanten Elastizitäten. Eine
Erhöhung (Senkung) des Preises um 1 % hat eine Nachfrageänderung in gleicher Größenordnung
zur Folge.
  x '(P) 
Beispiel 2:
Die Nachfrage x nach einem Gut kann in Abhängigkeit vom Verkaufspreis P durch folgende Funktion wiedergegeben werden: x(P) =  2P + 24 mit 0  P  12. Zum aktuellen Preis von 2 € ergibt
sich also ein Absatz von N(2) = 20 ME. Um welchen Prozentsatz verändert sich die Nachfrage,
wenn der Preis um 1 % erhöht wird?
Diese Fragestellung kann man mit Hilfe der Punktelastizität beantworten. Es gilt:

P
P 2P
  x '(P)   2  
x
x
x

2P
22

 0,2 .
Im Punkt P = 2 mit x(2) = 20 beträgt damit die direkte Punktelastizität   
x
20
Die Nachfrage wird um 0,2 % abnehmen. Sie ist damit unelastisch.
Diese Lösung kann man auch konventionell überprüfen:
Steigt der Preis um 1 %, ist der neue Preis 2,02 €. Eingesetzt in die Nachfragefunktion ergibt sich
eine Absatzmenge von N(2,02) = 19,96 ME. Das entspricht einem Rückgang um 0,4 ME oder von
0,2 %.