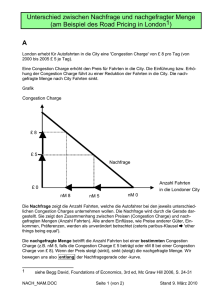
¨Ubungen zur Vorlesung Kommunikation in Parallelen

Rolf Wanka
Erlangen, 4. Mai 2011
Übungen zur Vorlesung
Kommunikation in Parallelen Rechenmodellen
SS 2012
Blatt 3
AUFGABE 9:
Eine Separation eines ungerichteten zusammenhängenden Graphen G = (V, E) ist eine disjunkte
Aufteilung von V in drei Mengen
V1 , V2 und
R, so daß kein Knoten aus V1 mit einem Knoten aus
V2 verbunden ist, und daß gilt |V1 | − |V2 | ≤ 1. Ziel einer Separation ist es, die Menge R so klein
wie möglich zu wählen.
In dieser Aufgabe soll eine kleine Menge R für den Hypercube M(2, d) konstruiert werden. Zeigen
Sie:
(a) R = {w | w enthält ⌈d/2⌉ oder ⌊d/2⌋ Einsen} liefert eine Separation von M(2, d).
2d (b) |R| = Θ √
d
n n √
1 · 1+
(Stirlingsche Formel)
Hinweis: n! ≈ 2πn ·
e
12n
AUFGABE 10:
Das Dimension-Order-Routing für das Permutationsrouting auf M(n, d) arbeitet folgendermaßen:
Durchlaufe alle Dimensionen in der Reihenfolge 0, . . . , d − 1. Wenn man in der Dimension δ arbeitet, sollen die Pakete in den linearen Arrays der Dimension δ so umverteilt werden, daß alle
Komponenten 0, . . . , δ der Zieladressen bereits erreicht sind. Dieses Verfahren ist die Verallgemeinerung der Lösung der zweiten Präsenzaufgabe von Blatt 1.
Die Permutation Indexdrehung I : [n]d → [n]d ist folgendermaßen definiert:
I(ad−1 . . . a0 ) = (a0 . . . ad−1 ) .
Sei N = nd . Bestimmen Sie die Congestion der Indexdrehung bzgl. Dimension-Order-Routing auf
M(n, d).
Zur Definition der Congestion einer Permutation π bzgl. Routingprotokoll R auf Netzwerk M:
Sei e eine Kante von M. Die Congestion von e und π bzgl. R auf M ist die Anzahl der Pakete, die
über e laufen. Die Congestion von π bzgl. R auf M ist das Maximum der Congestions über alle
Kanten.
AUFGABE 11:
(a) Bubblesort sollte Ihnen aus dem Grundstudium noch wohlbekannt sein. Entwerfen Sie ein
Vergleichsnetzwerk, das diesen Algorithmus implementiert“ (welches Prozessornetzwerk
”
mit n Prozessoren ist besonders geeignet, diese Vergleichsnetzwerke zu simulieren?). Wie
tief ist das Netzwerk?
(b) Die folgenden Vergleichsnetzwerke heißen OETL (4) und OETR (4) der Tiefe 4. OET steht
dabei für Odd Even Transpotion Sort.
Für beliebige n sind dann analog OETL (n) und OETR (n) der Tiefe n definiert.
Zeigen Sie ohne Anwendung des 0-1-Prinzips: OETL (n) und OETR (n) sind Sortiernetzwerke
der Tiefe n für n Zahlen.
Hinweis: Nehmen Sie o. B. d. A. an, daß alle Zahlen verschieden sind, und verfolgen den Weg
des Maximums durch das Netzwerk.