Junior Euler Society Rämibühl Aufgabenblatt 11

Junior Euler Society
Rämibühl
Aufgabenblatt 11
Aufgabe 1
Peter und Louise wollen folgende Behauptung beweisen:
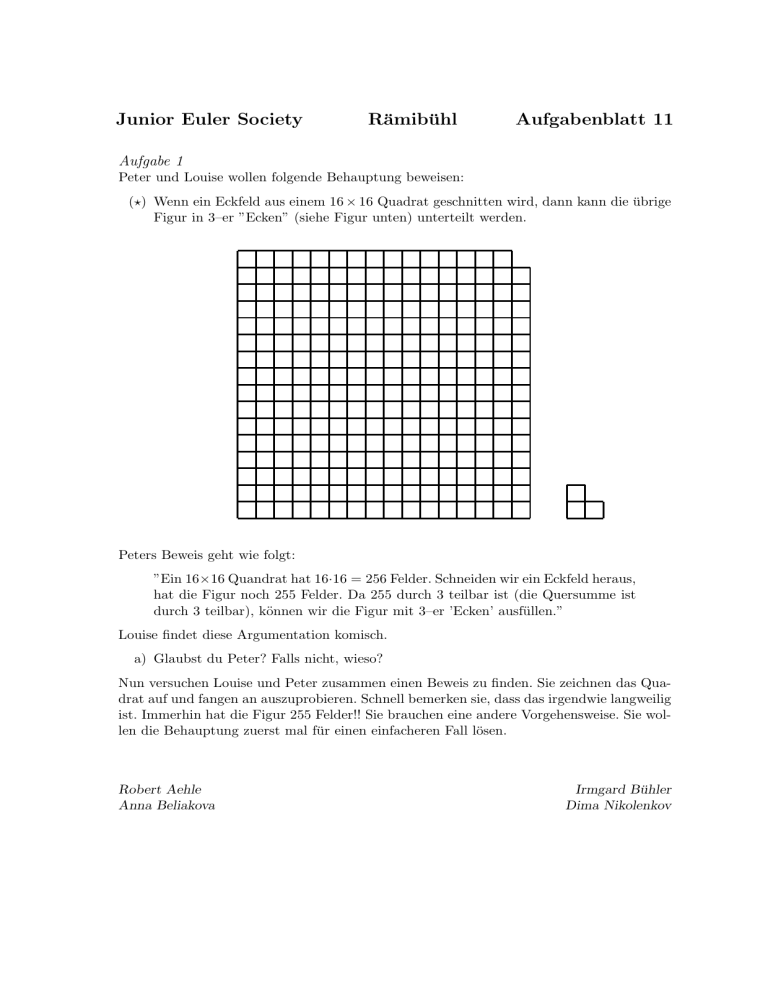
(⋆) Wenn ein Eckfeld aus einem 16 × 16 Quadrat geschnitten wird, dann kann die übrige
Figur in 3–er ”Ecken” (siehe Figur unten) unterteilt werden.
Peters Beweis geht wie folgt:
”Ein 16×16 Quandrat hat 16·16 = 256 Felder. Schneiden wir ein Eckfeld heraus,
hat die Figur noch 255 Felder. Da 255 durch 3 teilbar ist (die Quersumme ist
durch 3 teilbar), können wir die Figur mit 3–er ’Ecken’ ausfüllen.”
Louise findet diese Argumentation komisch.
a) Glaubst du Peter? Falls nicht, wieso?
Nun versuchen Louise und Peter zusammen einen Beweis zu finden. Sie zeichnen das Quadrat auf und fangen an auszuprobieren. Schnell bemerken sie, dass das irgendwie langweilig
ist. Immerhin hat die Figur 255 Felder!! Sie brauchen eine andere Vorgehensweise. Sie wollen die Behauptung zuerst mal für einen einfacheren Fall lösen.
Robert Aehle
Anna Beliakova
Irmgard Bühler
Dima Nikolenkov
b) Hast du einen Vorschlag? Suche eine Behauptung, welche ähnlich ist wie die Behauptung (⋆), aber welche einfacher ist zu lösen. Suche eine möglichst einfache (das heisst
mit möglichst kleiner Komplexität).
Sagen wir, deine Behauptung bekommt den Namen B1.
c) Finde eine Lösung zur Behauptung B1.
d) Was ist die nächst schwierigere Behauptung?
Diese Behauptung nennen wir nun B2.
e) Löse Behauptung B2. Kannst du dazu die Lösung von B1 benutzen?
f) Was ist die nächst schwierigere Behauptung?
Diese Behauptung nennen wir B3.
g) Löse die Behauptung B3. Benutze dazu, dass du bereits weisst, dass die Behauptung
B2 richtig ist.
h) Beweise die Behauptung (⋆) vom Anfang.
i) Was sind die nächst schwierigeren Behauptungen?
j) Kannst du auch alle diese beweisen?
k) Formuliere eine Behauptung Bn, welche alle bisherigen Behauptungen einschliesst.
Dabei kann n jede natürliche Zahl ≥ 1 annehmen. Kannst du Bn beweisen?
Löse folgende Aufgaben auf eine ähnliche Art und Weise. Reduziere immer zuerst die
Komplexität der Aufgaben und benutze dann die Lösung der einfacheren Aufgabe um die
Schwierigere zu lösen, respektive um einen allgemeinen Beweis zu finden.
Aufgabe 2
Zeige, dass die Zahl 111 . . . 111 (243 Einsen) durch 243 teilbar ist. (Tipp: 243 = 35 ).
Robert Aehle
Anna Beliakova
Irmgard Bühler
Dima Nikolenkov
Aufgabe 3
Susanne spielt ”Die Türme von Hanoi”: Auf einem Holzbrett befinden sich 3 Stäbe (siehe
Figur unten). Auf dem Stab ganz links stapeln sich eine bestimmte Anzahl Ringe. Diese
sind unterschiedlich gross und der Grösse nach angeordnet (der grösste Ring zuunterst).
Es darf immer der oberste Ring von einem Stab genommen und auf einen andern gesteckt
werden, aber es darf nie ein grösserer Ring auf einem Kleineren liegen. Ziel des Spiels ist,
die Ringe so zu verschieben, dass am Schluss alle auf dem mittleren Stab stecken.
a) Angenommen, es hat 2 Ringe. Wie oft musst du umstecken, um die Endposition zu
erhalten?
b) Wie oft brauchst du mit 3 (respektive mit 4) Ringen?
c) Angenommen, es hat n Ringe. Susanne behauptet, dass sie nur 2n − 1 mal umstecken
muss. Kann das sein?
*d) Zeige, dass es nicht möglich ist, das Spiel mit weniger als 2n − 1 mal umstecken zu
beenden.
Aufgabe 4
Berechne n2 + n + 41 für n = 1, 2, 3, 4 und 5. Glaubst du, dass n2 + n + 41 immer eine
Primzahl ist für jede natürliche Zahl n?
Aufgabe 5
Zum Zeitpunkt t = 0 stehen an der Wandtafel zwei Zahlen 1 und 1 geschrieben. Jede Minute schreibt man zwischen den vorhandenen Zahlen die Summe der beiden Nachbarn.
So stehen an der Tafel
zum Zeitpunkt t = 1 drei Zahlen 1, 2 und 1;
Die Anzahl Zahlen an der Tafel ist a1 = 3
zum Zeitpunkt t = 2 sieht man 5 Zahlen 1, 3, 2, 3 und 1.
a2 = 5
a) Schreibe die Folge der Zahlen, die man an der Tafel zum Zeitpunkt t = 3 und t = 4
sieht.
b) Stelle eine Vermutung auf wie viele Zahlen an sind an der Tafel zum Zeitpunkt t = n
zu sehen.
c) Wie viele Zahlen a20 stehen an der Tafel zum Zeitpunkt t = 20?
Robert Aehle
Anna Beliakova
Irmgard Bühler
Dima Nikolenkov
Methode der Induktion.
Wir gehen von einer Reihe von Behauptungen B1, B2, B3, ... aus. Wir schreiben nun eine
allgemeine Behauptung Bn auf, wobei n jede natürliche Zahl ≥ 1 annehmen kann. Wir
beweisen folgendes:
1) (Verankerung) Wir beweisen B1.
2) (Induktionsschritt) Wir beweisen B(n+1) unter der Annahme, dass Bn richtig ist.
Damit haben wir alle Behauptungen B1, B2, B3, B4, ... bewiesen. Zum Beispiel B4 ist
richtig, weil
B1
B2
B3
B4
ist richtig (Verankerung).
folgt aus B1 (Induktionsschritt), und B1 ist richtig. Also ist B2 richtig.
folgt aus B2 (Induktionsschritt), und B2 ist richtig. Also ist B3 richtig.
folgt aus B3 (Induktionsschritt), und B3 ist richtig. Also ist B4 richtig.
B3
B2
B4
B6
B5
B1
Beispiel: Für alle natürlichen Zahlen n gilt: Die Summe aller ungeraden Zahlen von 1 bis
2n − 1 ist gleich n2 .
B1
B2
B3
B4
...
Bn
B(n+1)
:
:
:
:
1 = 11
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7 = 42
: 1 + 3 + 5 + 7 + . . . + (2n − 3) + (2n − 1) = n2
: 1 + 3 + 5 + 7 + . . . + (2n − 1) + (2n + 1) = (n + 1)2
1) Verankerung: 1 = 12 ist richtig, also ist B1 richtig.
2) Induktionsschritt: Wir nehmen an, dass 1 + 3 + 5 + 7 + . . . + (2n − 1) = n2 (das heisst,
wir nehmen an, dass Bn richtig ist). Nun wollen wir B(n+1) beweisen:
1 + 3 + 5 + 7 + . . . + (2n − 1) + (2n + 1) = 1 + 3 + 5 + 7 + . . . + (2n − 1) +(2n + 1)
{z
}
|
=n2 , da Bn richtig
= n2 + 2n + 1
= (n + 1)2
Somit ist auch B(n+1) richtig. Damit haben wir alle Behauptungen bewiesen.
Robert Aehle
Anna Beliakova
Irmgard Bühler
Dima Nikolenkov