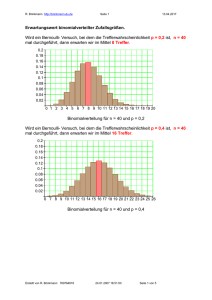
Seite 1
Werbung
EdM Elemente der Mathematik Lineare Algebra/Analytische Geometrie, Stochastik Rheinland-Pfalz (ISBN 978-3-507-87956-0) Seite 1 Leistungskurs Stochastik – Unterrichtsvorschlag Seiten 226-233 Vorgaben des Lehrplans 234-235 4.1.1 Wahrscheinlichkeit als zu erwartende relative Häufigkeit – Empirisches Gesetz der großen Zahlen Exkurs: Axiome der Wahrscheinlichkeitsrechnung Zufallsexperimente durch ihre Ergebnismengen beschreiben – Wahrscheinlichkeiten bestimmen und in Sachzusammenhängen interpretieren 236-241 4.1.2 Bestimmen von Wahrscheinlichkeiten durch Simulation Zufallsexperimente mit Hilfe von Zufallszahlen simulieren und die Ergebnisse der Simulation interpretieren 242-253 4.2 Mehrstufige Zufallsversuche Rechenregeln zur Bestimmung der Wahrscheinlichkeiten von Ereignissen begründen und anwenden 254-267 4.3 Mehrfeldertafeln – Bedingte Wahrscheinlichkeiten Die Begriffe “bedingte Wahrscheinlichkeit” und “Unabhängigkeit zweier Ereignisse” kennen und anwenden 272-276 5.1 Zufallsgrößen und Erwartungswert Die Begriffe „Zufallsgröße und “Wahrscheinlichkeitsverteilung” kennen und an Beispielen erläutern. – Die Begriffe “Erwartungswert“ einer diskreten Zufallsgröße kennen und anwenden. 277-280 281-286 287-291 292-296 5.2.1 BERNOULLI-Ketten 5.2.2 BERNOULLI-Formel 5.2.3 Kumulierte Binomialverteilungen 5.2.4 Erwartungswert einer Binomialverteilung Die Begriffe „Bernoullikette“, „Binomialverteilung“ verstehen und die Formel zur Berechnung der Werte einer Binomialverteilung herleiten – Eigenschaften der Binomialverteilung kennen, begründen und anwenden. Die Formeln für Erwartungswert und Standardabweichung einer Binomialverteilung kennen und anwenden 297-299 300-305 306-307 5.3.1 Anwendung der Binomialverteilung – Ein Auslastungsmodell 5.3.2 Anwendung der Binomialverteilung – Das Kugel-Fächer-Modell Blickpunkt: Das Problem der vollständigen Serie Sachaufgaben zur Binomialverteilung lösen 308-312 313-315 5.4.1 Varianz und Standardabweichung von Zufallsgrößen 5.4.2 Umgebungen um den Erwartungswert einer Binomialverteilung – Sigma-Regeln 6.1 Schluss von der Gesamtheit auf die Stichprobe Erwartungswert und Standardabweichung für Binomialverteilungen berechnen und anwenden. Die Begriffe „Erwartungswert“, „Varianz“ und „Standardabweichung“ einer diskreten Zufallsgröße kennen und anwenden. 320-328 EdM Elemente der Mathematik Lineare Algebra/Analytische Geometrie, Stochastik Rheinland-Pfalz (ISBN 978-3-507-87956-0) Seite 2 Leistungskurs Stochastik – Unterrichtsvorschlag Seiten Vorgaben des Lehrplans 329-346 346-347 6.2 Testen von Hypothesen Blickpunkt: Alternativtest Die Struktur des Hypothesentests verstehen – Sachaufgaben zum Testen von Hypothesen lösen und die Ergebnisse interpretieren 348-352 6.3.1 Schluss von der Stichprobe auf die Gesamtheit (Konfidenzintervalle) Den Begriff „Konfidenzintervall“ und das Verfahren zur Bestimmung eines Konfidenzintervalls für eine unbekannte Wahrscheinlichkeit verstehen – Sachaufgaben zu Konfidenzintervallen lösen und die Ergebnisse interpretieren 353-356 6.3.2 Wahl eines genügend großen Stichprobenumfangs Den Zusammenhang zwischen dem Stichprobenumfang und der Länge des Konfidenzintervalls verstehen 359-365 366-369 370-374 6.4.1 Approximation von Binomialverteilungen durch Normalverteilungen 6.4.2 Normalverteilte Zufallsgrößen – selbst lernen 6.4.3 Bestimmen der Kenngrößen bei normalverteilten Zufallsgrößen Verstehen, wie man Wahrscheinlichkeiten einer binomialverteilten Zufallsgröße näherungsweise mit Hilfe der Gaußschen Integralfunktion Φ (Standard-Normalverteilung) bestimmt – Funktionsterm, Graph und Eigenschaften der Gaußfunktion ϕ kennen