Kapitel 6 Grenzwerte von Funktionen und Stetigkeit Relle

Relle Funktionen
Im Folgenden betrachten wir reelle Funktionen
f : D −→ R, mit D ⊆ R.
Kapitel 6
Grenzwerte von Funktionen und Stetigkeit
Wir suchen eine formale Definition für den folgenden Sachverhalt.
Eine Funktion f (x) nähert sich dem Grenzwert l bei x = a an.
225
226
Umgebung
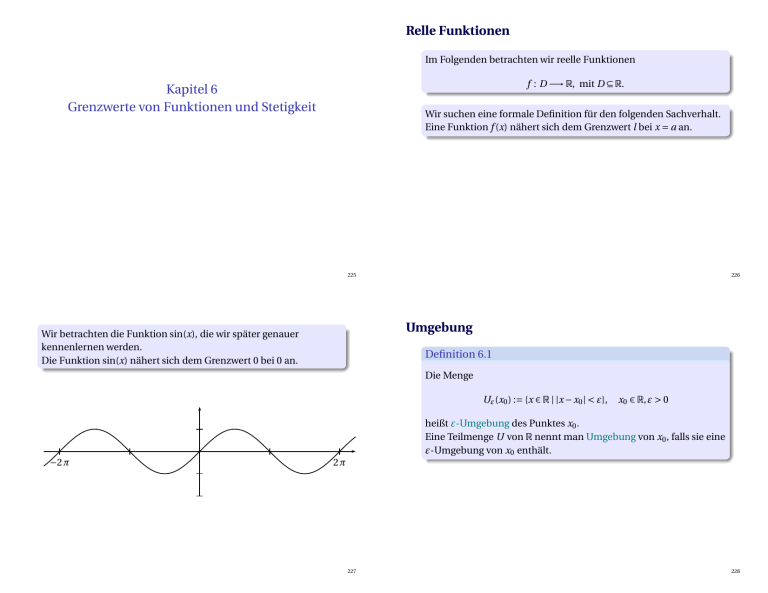
Wir betrachten die Funktion sin(x), die wir später genauer
kennenlernen werden.
Die Funktion sin(x) nähert sich dem Grenzwert 0 bei 0 an.
Definition 6.1
Die Menge
Uε (x0 ) := {x ∈ R | |x − x0 | < ε},
x0 ∈ R, ε > 0
heißt ε-Umgebung des Punktes x0 .
Eine Teilmenge U von R nennt man Umgebung von x0 , falls sie eine
ε-Umgebung von x0 enthält.
−2 π
2π
227
228
Betrachte nun die Funktion x · sin(1/x), die auf R \ {0} definiert ist.
Betrachte nun die Funktion sin(1/x), die auf R \ {0} definiert ist.
Die Funktion nähert sich keinem Grenzwert bei 0 an.
Was ist hier das Problem? Jede Umgebung von 0 enthält Punkte x∗
mit sin(1/x∗ ) = 1 und Punkte y ∗ mit sin(1/y ∗ ) = −1.
229
Grenzwerte von Funktionen, formale Definition
lim f (x) = l,
Der Punkt a ist Häufungspunkt von D ⊆ R, wenn jede Umgebung
von a einen Punkt aus D \ {a} enthält.
x→a
wenn es für jedes ε > 0 ein δ > 0 gibt mit
Definition 6.3
f (Uδ (a) ∩ D \ {a}) ⊆ Uε (l).
Sei a ein Häufungspunkt des Definitionsbereichs D der Funktion f .
Die Funktion f hat bei a den Grenzwert l, wenn für jedes ε > 0 ein
δ > 0 existiert, sodass für alle x ∈ D gilt
=⇒
230
Ausgedrückt in der Terminologie von Umgebungen gilt also für
einen Häufungspunkt a von D
Definition 6.2
0 < |x − a| < δ
Sei ε > 0 und setze δ := ε. Dann gilt für alle x ∈ R \ {0} mit |x| < δ auch
|x · sin(1/x)| É |x| < ε. In der δ-Umgebung um 0 haben die
Funktionswerte höchstens Abstand ε von 0. Die Funktion nähert
sich dem Grenzwert 0 bei 0 an.
|f (x) − l| < ε.
Wir schreiben dann
lim f (x) = l.
x→a
231
232
Beispiel 6.4
Beispiel 6.5
Betrachte die Funktion x · sin(1/x). Der Definitionsbereich der
Funktion ist D = R \ {0}. Der Punkt a = 0 ist ein Häufungspunkt von
D.
Wir zeigen nun limx→0 x · sin(1/x) = 0.
Dazu sei ε > 0 vorgegeben. Wir suchen ein δ > 0 mit
Betrachte die Funktion f : R → R definiert durch
f (x) =
Setze δ := ε. Dann gilt für x mit 0 < |x| < δ
=
=
É
<
0,
falls x < 0
1,
falls x Ê 0
Der Grenzwert limx→0 f (x) existiert nicht.
Denn nehmen wir einmal an, dieser wäre l.
Setze ε := max{|l − 1|, |l|}/2.
Für alle δ > 0 existieren x1 , x2 ∈ Uδ (0) \ {0} mit f (x1 ) = 1 und f (x2 ) = 0.
Es gilt
∀x ∈ D 0 < |x| < δ =⇒ |x · sin(1/x)| < ε.
|x · sin(1/x) − 0|
(
|x · sin(1/x)|
|x| · | sin(1/x)|
max{|l − f (x1 )|, |l − f (x2 )|} =
|x|
>
δ.
max{|l − 1|, |l|}
ε.
Und somit ist f (x1 ) oder f (x2 ) nicht in Uε (l).
234
233
Lemma 6.6
Beispiel 6.7
Betrachte die Funktion
In einer beliebigen Umgebung einer rationalen Zahl a liegen
irrationale Zahlen.
In einer beliebigen Umgebung einer irrationalen Zahl b liegen
rationale Zahlen.
f (x) =
(
x,
falls x ∈ R \ Q,
0, sonst.
Jeder Punkt ist ein Häufungspunkt des Definitionsbereichs. Es gilt
limx→0 f (x) = 0.
Sei ε > 0. Setze δ := ε. Wenn |x| < δ, dann gilt auch |f (x)| < ε.
Für a 6= 0 existiert limx→a f (x) nicht. Denn nehmen wir an, dieser
Grenzwert sei l.
Wenn l = 0, dann betrachte ε = |a|/4. Für jedes δ > 0 existiert ein
irrationales x mit 0 < |x − a| < δ Insbesondere existiert in Uδ (a) \ {a}
ein x∗ ∈ R \ Q mit |x∗ | > |a/2|. D.h. l = 0 ist unmöglich.
Wenn l 6= 0, dann betrachte ε = |l|/2. In jeder Umgebung Uδ (a) mit
δ > 0 existiert eine rationale Zahl x∗ 6= a. Es gilt f (x∗ ) = 0 und somit
|f (x∗ ) − l| > ε.
Beweis.
Sei a eine rationale Zahl.
p
Die Zahl a + 2/n ist irrational und wenn n genügend groß, beliebig
nahe an a.
Sei b eine reelle irrationale Zahl. Die Zahl ⌈n · b⌉/n hat zu b Abstand
É 1/n.
235
236
Satz 6.8 (Folgenkriterium)
Aus dem Wissen über Folgen können wir mit Satz 6.13 bereits einige
Rechenregeln herleiten.
Sei f : D −→ R eine Funktion und a ein Häufungspunkt von D. Es gilt
limx→a f (x) = l genau dann, wenn für jede Folge (xn )n∈N in D \ {a} mit
limn→∞ xn = a auch
lim f (xn ) = l
Satz 6.9
Es seien die Funktionen f , g : D → R gegeben und a ein
Häufungspunkt von D. Wenn limx→a f (x) = α und limx→a g(x) = β
dann gilt
n→∞
gilt.
i) limx→a (f + g)(x) = α + β
Bemerkung 16
ii) limx→a (f · g)(x) = α · β
Der Grenzwert einer Funktion bei a ist eindeutig.
iii) Wenn β 6= 0, dann gilt limx→a (f /g)(x) = α/β
237
Stetigkeit
238
Beispiel 6.11
Die Funktion f : R → R, f (x) = x2 , ist stetig in jedem Punkt x0 ∈ R. Es
gilt:
Definition 6.10
Eine Funktion f : D → R heißt stetig im Punkt x0 ∈ D, wenn es für
jedes ε > 0 ein δ > 0 gibt mit
|f (x) − f (x0 )| = |x2 − x02 | É |x + x0 ||x − x0 | É (2|x0 | + 1)|x − x0 |
für |x − x0 | < 1. Zu einem gegebenen ε > 0 setzen wir
f (Uδ (x0 ) ∩ D) ⊆ Uε (f (x0 )).
δ = min{
Mit anderen Worten bedeutet dies, f : D → R ist stetig im Punkt
x0 ∈ D, wenn es für jedes ε > 0 ein δ > 0 gibt mit
∀x ∈ D
|x − x0 | < δ
ε
, 1}.
2|x0 | + 1
Dann gilt in der Tat
=⇒ |f (x) − f (x0 )| < ε.
|x − x0 | < δ ⇒ |f (x) − f (x0 )| < ε.
Bemerkung 17
f ist also stetig im Punkt x0 ∈ D, falls x0 kein Häufungspunkt von D
ist, oder falls
lim f (x) = f (x0 )
x→x0
239
240
Beispiel 6.12
Das Folgenkriterium für Grenzwerte impliziert die Folgenstetigkeit.
Betrachte die Dirichletsche Sprungfunktion f : R → R gegeben durch
f (x) =
(
1,
falls x rational ist
0,
andernfalls.
Satz 6.13 (Folgenstetigkeit)
Sei f : D −→ R eine Funktion und x0 ∈ D. Die Funktion f ist stetig im
Punkt x0 genau dann, wenn für jede Folge (xn )n∈N in D mit
limn→∞ xn = x0 auch
lim f (xn ) = f (x0 )
Diese Funktion ist in keinem Punkt stetig!
n→∞
gilt.
Satz 6.14
Seien X , Y , Z ⊆ R. Sind f : X → Y stetig (im Punkt x0 ) und g : Y → Z
stetig (im Punkt y0 := f (x0 )), so ist auch die zusammengesetzte
Funktion g ◦ f stetig (im Punkt x0 ).
241
242
Definition 6.16
Änlich wie die Rechenregeln für Grenzwerte schließt man auch den
folgenden Satz.
Sind a0 , a1 , . . . , ad vorgegebene reelle Zahlen, so wird durch
p(x) := a0 + a1 x + . . . + ad xd
Satz 6.15
Sind die Funktionen f , g : D → R stetig (im Punkt x0 , so sind auch die
Funktionen
f
f + g, λ · f (λ ∈ K ), f · g, , |f |
g
eine Funktion p : R → R definiert.
Eine derartige Funktion heißt Polynomfunktion.
Die aν sind die Koeffizienten von p.
Gilt ad 6= 0, so nennt man d den Grad von p.
stetig (im Punkt x0 ). Bei der Division muss natürlich g(x0 ) 6= 0
vorausgesetzt werden.
Folgerung 6.17
Polynomfunktionen sind stetig.
Bemerkung 18
Eine Polynomfunktion bestimmt ihre Koeffizienten eindeutig.
243
244
Satz 6.20
Definition 6.18
Eine rationalen Funktion ist ein Quotient zweier
Polynomfunktionen p und q, wobei q nicht die Nullfunktion sein
darf:
p(x)
.
r(x) :=
q(x)
Sei f : X → R stetig im Punkt x0 und f (x0 ) > 0. Dann gibt es eine
Umgebung U von x0 mit
∀x ∈ U ∩ X
f (x) > 0.
Die Funktion r ist überall definiert, ausser bei den Nullstellen x von
q, charakterisiert durch q(x) = 0.
Folgerung 6.19
Rationale Funktionen sind stetig.
245
246
Definition 6.21
Unter einem kompaktem Intervall verstehen wir ein beschränktes
und abgeschlossenes Intervall X = [a, b].
Kapitel 6.1
Hauptsätze über stetige Funktionen
Satz 6.22 (Satz vom Maximum)
Ist f : X → R stetig und X ein kompaktes Intervall, so nimmt f auf X
ein globales Maximum an. D.h. es gibt einen Punkt ξ ∈ X mit
f (x) É f (ξ) für alle x ∈ X .
Folgerung 6.23
Ist f : X → R stetig und X ein kompaktes Intervall, so nimmt f auf X
ein globales Minimum an. D.h. es gibt einen Punkt ξ ∈ X mit
f (x) Ê f (ξ) für alle x ∈ X .
247
248
Definition 6.24
Satz 6.25 (Zwischenwertsatz)
Eine Teilmenge X ⊆ R heisst abgeschlossen, wenn sie alle ihre
Häufungspunkte enthält.
Die Teilmenge X heisst beschränkt, wenn ein R existiert mit |x| É R
für alle x ∈ X .
Beschränkte und abgeschlossene Teilmengen heissen kompakt.
Es sei f : [a, b] → R stetig und f (a) < f (b). Dann nimmt die Funktion f
jeden Zwischenwert c im Intervall [f (a), f (b)] an, d.h. zu jedem
Zwischenwert c gibt es ein x ∈ [a, b] mit c = f (x).
Folgerung 6.26
Jede Polynomfunktion ungeraden Grades d
p(x) = xd + ad−1 xd−1 + . . . + a1 x + a0
besitzt wenigstens eine reelle Nullstelle, d.h. ein x ∈ R mit p(x) = 0.
250
249
Definition 6.27
Beispiel 6.29
Es sei n ∈ N, n Ê 1. Die Potenzfunktion
Wir nennen eine reelle Funktion f : [a, b] → R streng monoton
wachsend, wenn f (x) < f (x′ ) für alle x < x′ gilt.
f : [0, ∞[→ [0, ∞[, f (x) = xn
Bemerkung 19
ist streng monoton wachsend und stetig. Der Satz von der
Umkehrfunktion zeigt die Existenz und Stetigkeit der n-ten
p
Wurzelfunktion g(y) = n y als Umkehrfunktion von f .
Solche Funktionen sind offenbar injektiv.
Satz 6.28 (von der Umkehrfunktion)
Es sei f : [a, b] → R streng monoton wachsend und stetig. Dann bildet
f das Intervall [a, b] bijektiv auf das Intervall [f (a), f (b)] ab. Die
Umkehrfunktion
g := f −1 : [f (a), f (b)] −→ [a, b]
ist ebenfalls streng monoton wachsend und stetig.
251
252