mathematik basics mathematik basics

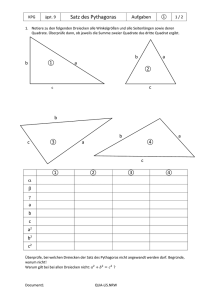
reichen zu Beginn der beruflichen Grundbildung vorausgesetzt
wird.
Die Reihe Mathematik Basics bietet in zehn Bänden eine syste­
matische, übersichtliche Einführung in die wichtigsten Gebiete
der Mathematik.
Sie richtet sich vor allem an die folgenden Zielgruppen:
− Schulabgängerinnen und Schulabgänger der Volksschule,
insbesondere 10. Schuljahr / Brückenangebote
− Lernende zu Beginn der beruflichen Grundbildung
– Lernende in Förderkursen
– Erwachsene in der beruflichen Weiterbildung, die sich
mathe­matisches Basis­wissen aneignen wollen.
In allen technisch-konstruktiven Berufen sind die Kenntnisse
der Dreieckslehre von grosser Bedeutung.
Zu Beginn dieses Lehrmittels wird der Satz des Pythagoras
behandelt, obwohl die Theorie zur Planimetrie gehört. In recht­
winkligen Dreiecken können Winkel und Seiten mithilfe der drei
trigonometrischen Funktionen Sinus, Kosinus und Tangens
ermittelt werden. Nach der Erarbeitung der Grundlagen der
Trigonometrie werden viele unterschiedliche Beispiele be­rech­
net.
Aufbauend auf den Gesetzen der trigonometrischen Funktionen
rechtwinkliger Dreiecke werden dann Sinus- und Kosinussatz
an nicht rechtwinkligen Dreiecken aufgezeigt. In Beispielen
werden die beiden Sätze praktisch angewendet, und in den
letzten sechs Übungssequenzen wächst der Schwierigkeits­
grad kontinuierlich.
MATHEMATIK BASICS
ziellen Kompetenz, welche in den verschiedensten Berufsbe­
MATHEMATIK BASICS
Mathematisches Grundwissen zählt heutzutage zu einer essen­
Rainer Hofer, Marc Peter, Jean-Louis D’Alpaos
Trigonometrie
www.hep-verlag.ch/mathe-basics-trigonometrie
UG_MB_Trigonometrie_Schu_2A_15.indd 1
08.01.15 13:16
Vorwort
In allen technisch-konstruktiven Berufen sind die Kenntnisse der Dreieckslehre von
grosser Bedeutung.
Für Lernende, die Schwierigkeiten haben, dem Unterricht im Fachrechnen zu ­folgen,
­wurde dieses Lehrmittel – als Produkt langjähriger Erfahrungen im Bereich der
­Pädagogischen Fördermassnahmen (PFM) an Berufsfachschulen – entwickelt. Es ist
systematisch aufgebaut und ermöglicht einen handlungs- und ressourcenorientierten
Unterricht im Umfang von zirka 20 Lektionen. Ergänzend können Lehrpersonen auf der
Webseite des Verlags ein ausgefülltes Exemplar sowie Lernkontrollen freischalten und
herunterladen.
Zu Beginn dieses Lehrmittels wird der Satz des Pythagoras behandelt, obwohl die ­
Theorie zur Planimetrie gehört. Für viele Lernende ist dies vielleicht eine Repetition,
aber unabdingbar, um im letzten Kapitel den Kosinussatz zu verstehen.
Im rechtwinkligen Dreieck können Winkel und Seiten mithilfe der drei trigonometrischen
Funktionen Sinus, Kosinus und Tangens ermittelt werden. Am einfachen Beispiel ­einer
Strasse mit Steigung wird die Grundlage der Trigonometrie erarbeitet. Vom Seiten­
verhältnis über den Funktionswert bis zum Winkelwert werden alle Teilschritte aufgezeigt.
Mit diesem Grundlagenwissen und der selbst erarbeiteten Formelsammlung, werden nun
viele unterschiedliche Beispiele berechnet. Ganz besonderen Wert wird auf Skizzen gelegt,
weil alle Seiten und Winkel zuerst einmal bezeichnet werden müssen, bevor die eigentlichen Berechnungen vorgenommen werden können. Eine Vielzahl praktischer Übungen
ermöglicht eine Festigung des neu erlernten.
Aufbauend auf den Gesetzen der trigonometrischen Funktionen rechtwinkliger Dreiecke
werden nun Sinus- und Kosinussatz an nicht rechtwinkligen Dreiecken aufgezeigt. Dabei
beschränkt sich die Theorie bewusst auf den l. und II. Quadranten des Einheitskreises,
um wirklich bei den «Basics» zu bleiben, aber dennoch fundiert aufzubauen. In ­Beispielen
­werden die beiden Sätze praktisch angewendet, und in den letzten sechs Übungs­
sequenzen wächst der Schwierigkeitsgrad kontinuierlich.
Das Lehrmittel Trigonometrie ist bewusst Teil der Reihe Mathematik Basics, weil es
­zusammen mit den anderen Bänden die Grundlage fürs fachkundliche Rechnen ­bildet.
Dieses Lehrmittel kann in der beruflichen Grundbildung und in Förderkursen an der
­Berufsfachschule eingesetzt werden.
Mein grosser Dank gilt Marc Peter (1959–2011), der mich bei der Erstellung der
­Erst­ausgabe massgeblich unterstützt hat. Nun ist Jean-Louis D’Alpaos mein
­Brainstorming-Partner und unterstützt mich bei der Weiterentwicklung dieses Lehrmittels.
Rainer Hofer, Berufsschullehrer und Lehrperson für Förderangebote
Inhaltsverzeichnis
1
Rechtwinklige Dreiecke
Seite
6
1.1
Satz des Pythagoras
Seite
6
2
Winkelmessung und Einheitskreis
Seite 13
2.1
Winkelmessung
Seite 13
2.2
Einheitskreis
Seite 14
3
Trigonometrie rechtwinkliger Dreiecke
Seite 15
3.1
Grundlagen der Trigonometrie
Seite 15
3.2
Betrachtungswinkel in rechtwinkligen Dreiecken
Seite 15
3.3
Bespiel aus dem Alltag – Steigung m
Seite 16
3.4
Überblick der vier trigonometrischen Funktionen
Seite 18
3.5
Überblick Formeln
Seite 19
3.6
Beispiele von Berechnungen rechtwinkliger Dreiecke
Seite 20
3.7
Darstellung der Winkelfunktionen im I. Quadranten
Seite 26
3.8
Zusammenfassung der trigonometrischen Funktionen
Seite 29
4
Trigonometrische Funktionen von Winkeln über 90°
Seite 30
4.1
Begriff der Winkelfunktionen über 90°
Seite 30
4.2
Der Sinussatz
Seite 33
4.3
Beispiele zum Sinussatz
Seite 35
4.4
Der Kosinussatz
Seite 37
4.5
Beispiele zum Kosinussatz
Seite 38
4.6
Vermischte Aufgaben
Seite 40
Lösungen zu den Übungen
Trigonometrie
Seite 41
Seite 5
1
Rechtwinklige Dreiecke
Dreiecke, die einen rechten Winkel besitzen, spielen in der Geometrie eine besondere Rolle. Einmal wegen ihrer leichten Konstruierbarkeit (Thaleskreis), zum anderen
weil ihre Seiten in einer rechnerischen Beziehung zueinander stehen, was insbesondere im Lehrsatz des Pythagoras zur Geltung kommt. Dieses Wissen wurde für
Konstruktionen und Berechnungen verwendet, beispielsweise beim Bau der Pyramiden.
1.1 Satz des Pythagoras
Der Grieche Pythagoras lebte von ca. 570 v.Chr. bis 500 v.Chr. Er gründete in Kroton (Unteritalien) einen Bund mit religiösen, wissenschaftlichen, politischen und
ethischen Zielen (Pythagoreer). Man geht jedoch davon aus, dass der berühmte
„Satz des Pythagoras“ schon 1700 v.Chr. von den Babyloniern angewandt wurde.
Mit dem Satz des Pythagoras lässt sich eine Seite eines rechtwinkligen Dreiecks berechnen, wenn die beiden anderen Seiten bekannt sind.
Die Addition aller Winkel in einem Dreieck ergibt bekanntlich 180°. Da bei rechtwinkligen Dreiecken der rechte Winkel 90° beträgt, ist die Summe der beiden anderen
Winkel immer 180° 90° 90°. Mit Ausnahme des rechten Winkels müssen beim
Satz des Pythagoras keine anderen Winkel bekannt sein.
Bei der Bezeichnung rechtwinkliger Dreiecke gilt:
x Wie bei allen Dreiecken werden die drei Seiten a , b und c im Gegenuhrzeigersinn angeschrieben.
x Die längste Seite wird als Hypotenuse bezeichnet. Sie liegt immer dem rechten
Winkel gegenüber. Üblicherweise wird sie als die Seite c angegeben.
x Die beiden anderen Seiten a und b werden als Katheten bezeichnet. Sie bilden
zusammen den rechten Winkel.
Trigonometrie
Seite 6
Der Satz von Pythagoras besagt, dass die Flächen über den beiden Katheten zusammen gleich gross sind wie die Fläche über der Hypotenuse:
..............................................................
..............................................................
_____________________
..............................................................
..............................................................
Satz des Pythagoras:
Trigonometrie
.......................................................
Seite 7