Trigonometrie - edunai
Werbung

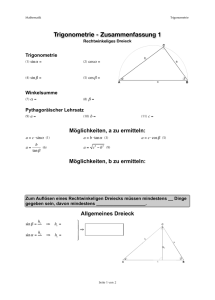
Trigonometrie Trigonometrie Arpad Dunai August 15, 2013 Trigonometrie Winkel in Dreiecken Grundregeln Grundregeln Bei allen Rechtwinkligen Dreiecken lassen sich der Satz der Pythagoras und die Trigonometrischen Grundregeln anwenden. A = Ankatete G = Gegenkatete H = Hypotenuse Divisionstabelle G A G H H A sin α cos α tan α Figure : Rechtwinklige Dreiecke G ; cos α = H G tan α = ; cot α = A sin α = A G cot α A H A G Trigonometrie Winkel in Dreiecken Grundregeln Dreiecke in anderen Dreiecken Wenn kein rechtwinkliges Dreieck vorliegt, kann man dennoch Trigonometrische Berechnungen vornehmen. Dazu zeichnet man die Höhe ein, was gleich zwei rechtwinklige Dreiecke ergibt. Aufgabe: Seite b und alle Winkel sind bekannt. Seite a soll berechnet werden. Figure : Beliebiges Dreieck h nimmt hier die Funktion der Gegenkatete ein und a und b sind die Hypotenusen der ’Unterdreiecke’. sin α = h → h = sin α · b b h h = sin β → a = a sin β Trigonometrie Winkel in Dreiecken Grundregeln Kernaussage Wenn man die Divisionstabelle von Seite 2 intus hat, geht es nur noch darum bei Aufgaben die richtigen Dreiecke zu finden! Ein Merksatz wäre ’GAGA HühnerHof AG → GAGA/HHAG. Trigonometrie Winkel in Dreiecken Sinussatz Sinussatz Der Sinussatz beschreibt eine Gesetzmässigkeit, die in jedem beliebigen Dreieck gegeben ist. Man kann ihn mit der Divisionstabelle herleiten, aber für Prüfungen empfielt es sich ihn auch auswendig zu lernen. a b c = = sin α sin β sin γ Figure : Beliebiges Dreieck Trigonometrie Winkel in Dreiecken Cosinussatz Cosinussatz Der Cosinussatz ist ein erweiterter Satz des Pythagoras. Die ’Erweiterung’ ermöglicht es Berechnungen durchzugühren, ohne dass das Dreieck einen rechten Winkel hat. Figure : Beliebiges Dreieck c 2 = a2 + b 2 − 2 · a · b · cos γ Für die anderen Seiten entsprechend: 2 2 2 b = a + c − 2 · a · c · cos β a2 = b 2 + c 2 − 2 · b · c · cos α Beim Satz der Pythagoras fällt der Zusatz weg, weil cos 90◦ = 0 ist und somit der ganze Zusatz gleich 0 wird. Trigonometrie Winkel in Dreiecken Wann Sinus-, wann Cosinussatz? Mit dem Sinussatz ist man bei den meisten Berechnungen schneller, da oft nur zwei der drei Gleichungsteile verwendet werden müssen. Wenn aber bei einem Dreieck alle Seiten gegeben sind, jedoch kein Winkel, dann kann man die Winkel nur mit dem Cosinussatz berechnen.